4.4探索活动:三角形的面积基础练习 北师大版数学五年级上册(含答案)
文档属性
| 名称 | 4.4探索活动:三角形的面积基础练习 北师大版数学五年级上册(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 548.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-09 00:00:00 | ||
图片预览



文档简介
/ 让教学更有效 精品试卷 | 数学
4.4探索活动:三角形的面积
学校:___________姓名:___________班级:___________考号:___________
一、填空题
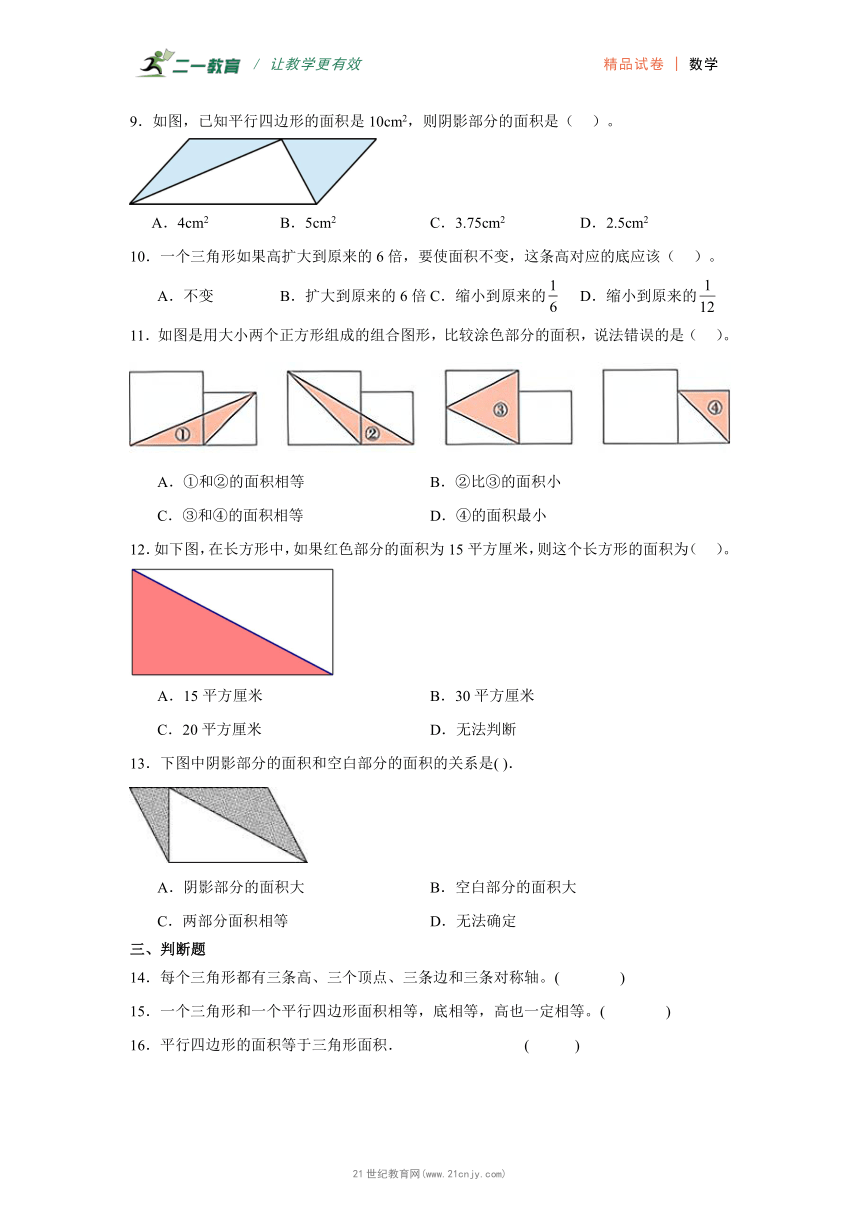
1.以正方形的4个顶点和正方形的中心(共5个点)为顶点,可以套出 种面积不等的三角形.
2.一个三角形,底为6分米,高为30厘米,它的面积是 .
3.如图中图 的面积与图①相等.
如图,平行四边形的面积是18平方分米,阴影部分两个三角形的面积是 .
如图:三条直线互相平行,l1与l3之间的距离是7厘米,l2上AB=4厘米.求阴影部分三角形的面积是 .
21·世纪*教育网
6.把一个三角形的底扩大到原来的2倍,高不变,面积就扩大到原来的 倍。
二、选择题
7.一个三角形的高是5cm,高对应的底增加8 cm,面积增加( )。
A.8 B.20 C.40 D.无法确定
8.如图,在等腰梯形中三角形甲的面积( )三角形乙的面积。
A.= B.> C.< D.无法确定
9.如图,已知平行四边形的面积是10cm2,则阴影部分的面积是( )。
A.4cm2 B.5cm2 C.3.75cm2 D.2.5cm2
10.一个三角形如果高扩大到原来的6倍,要使面积不变,这条高对应的底应该( )。
A.不变 B.扩大到原来的6倍 C.缩小到原来的 D.缩小到原来的
11.如图是用大小两个正方形组成的组合图形,比较涂色部分的面积,说法错误的是( )。
A.①和②的面积相等 B.②比③的面积小
C.③和④的面积相等 D.④的面积最小
12.如下图,在长方形中,如果红色部分的面积为15平方厘米,则这个长方形的面积为( )。
A.15平方厘米 B.30平方厘米
C.20平方厘米 D.无法判断
13.下图中阴影部分的面积和空白部分的面积的关系是( ).
A.阴影部分的面积大 B.空白部分的面积大
C.两部分面积相等 D.无法确定
三、判断题
14.每个三角形都有三条高、三个顶点、三条边和三条对称轴。( )
15.一个三角形和一个平行四边形面积相等,底相等,高也一定相等。( )
16.平行四边形的面积等于三角形面积. ( )
17.图形和的面积相等。( )
18.如图,这个三角形的底不变,高越大,面积越大。( )
四、解答题
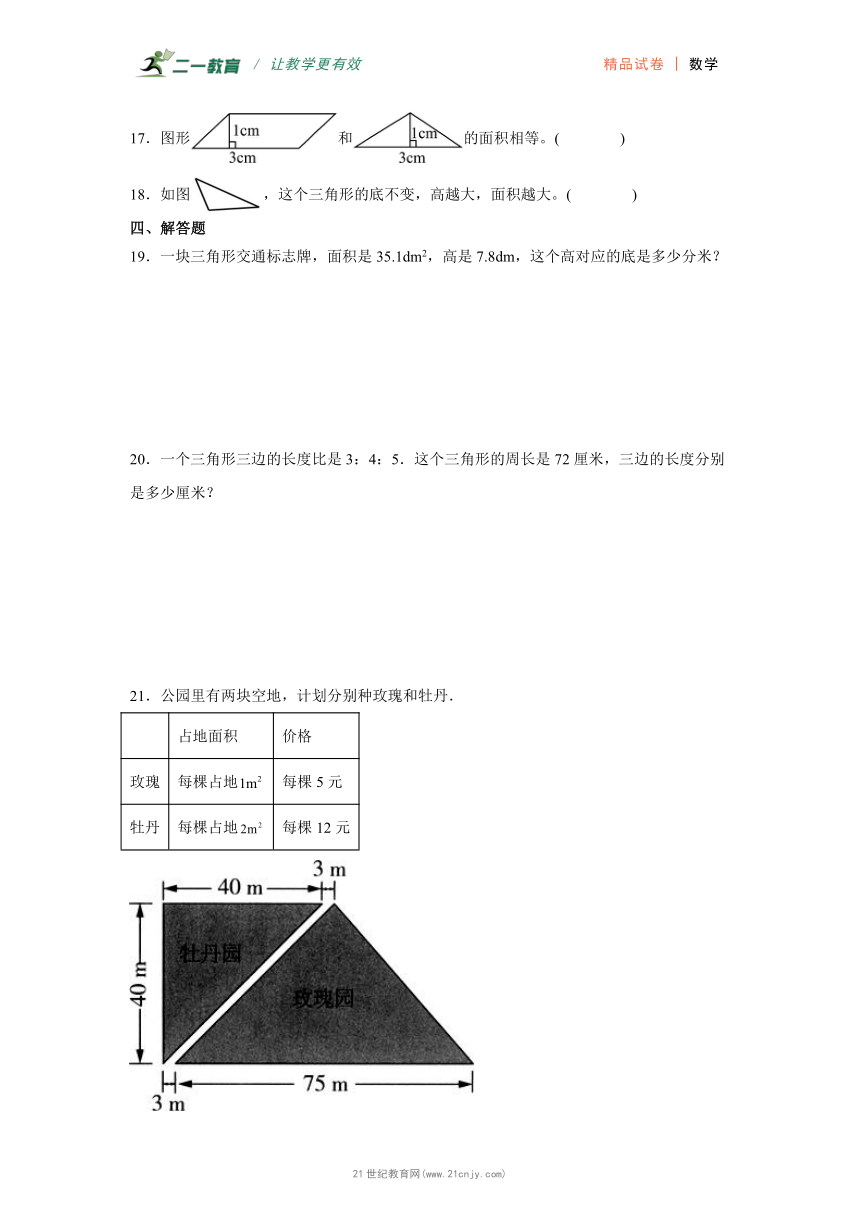
19.一块三角形交通标志牌,面积是35.1dm2,高是7.8dm,这个高对应的底是多少分米?
20.一个三角形三边的长度比是3:4:5.这个三角形的周长是72厘米,三边的长度分别是多少厘米?
21.公园里有两块空地,计划分别种玫瑰和牡丹.
占地面积 价格
玫瑰 每棵占地 每棵5元
牡丹 每棵占地 每棵12元
(1)玫瑰园占地多少平方米?种玫瑰一共需要多少元?
(2)你还能提出什么数学问题?并尝试解答.
22.有一个边长是2.4m正方形客厅,用三角形瓷砖(如图)铺满,需要多少块这种瓷砖?
23.如图,一个直角三角形花坛的面积是60平方米,一条直角边长15米,另一条直角边长多少米?
参考答案:
1.2
【详解】试题分析:要求可以套出几种面积不等的三角形,可分两种情况进行分析:(1)如果三个顶点全取正方形顶点,三角形面积和正方形面积的关系;(2)如果一个顶点取在正方形的中心,另两个点取正方形的顶点,三角形的面积和正方形面积的关系;
解:(1)如果三个顶点全取正方形顶点,则无论怎样套,三角形面积都是正方形面积的一半;
(2)如果一个顶点取在正方形的中心,则无论怎样套,三角形的面积都是正方形面积的;
所以面积不同的三角形共有2种.
答:可以套出2种面积不等的三角形;
故答案为2.
点评:解答此题的关键是先进行假设,进而通过假设得到的数据进行比较,进而得出结论.
2.9平方分米
【详解】试题分析:三角形的面积S=ah,据此代入数据即可求解.
解:30厘米=3分米,
6×3÷2=9(平方分米);
答:这个三角形的面积是9平方分米.
故答案为9平方分米.
点评:此题主要考查三角形的面积的计算方法的灵活应用.
3.③⑦
【详解】试题分析:根据长方形的面积=长×宽,梯形的面积=(上底+下底)×高÷2,正方形的面积=边长×边长,三角形的面积=底×高÷2,平行四边形的面积=底×高,以及利用图形的割补法求出图形⑦,是一个长5、宽3的长方形的面积,再与图形①的面积相比较即可解答问题.21教育网
解:图形①的面积是:3×5=15;
图形②的面积是:(5+2)×3÷2,
=7×3÷2,
=10.5;
图形③的面积是:(4+2)×5÷2,
=6×5÷2,
=15;
图形④的面积是:3×4=12;
图形⑤的面积是:4×4=16;
图形⑥的面积是:4×5÷2,
=20÷2,
=10;
图形⑦的面积是:3×5=15;
图形⑧的面积是:3×4=12.
所以与图形①的面积相等的是图形③和⑦.
故答案为③⑦.
点评:此题主要考查几种常见图形的面积公式的计算应用,熟记公式即可解答.
4.9平方分米
【详解】试题分析:由题意得:阴影部分面积=平行四边形的面积﹣空白三角形面积,空白三角形与平行四边形等底等高,所以空白三角形面积=平行四边形的面积÷2,代数计算即可.
解:18﹣18÷2,
=18﹣9,
=9(平方分米).
答:阴影部分两个三角形的面积是9平方分米.
故答案为9平方分米.
点评:解决本题的关键是明确空白三角形与平行四边形等底等高,所以空白三角形面积=平行四边形的面积÷2.21世纪教育网版权所有
5.14平方厘米
【详解】试题分析:
如上图,阴影部分的面积等于上面三角形△ABC的面积加上下面三角形△ABD的面积,假设l1和l2间的距离是h1,l2和l3间的距离是h2,根据三角形的面积公式,列出等式,都有底AB,提取公因数AB,h1+h2就是l1和l3间的距离7厘米,因此得解.
解:S△ABC+S△ABD=AB h1+AB h2=AB (h1+h2)=×4×7=14(平方厘米);
答:阴影部分三角形的面积是14平方厘米.
故答案为14平方厘米.
点评:此题的关键是面积之和,提取公因数,刚好和已知联系起来.
6.2
【分析】根据三角形的面积公式:S=ah和积的变化规律进行解答即可。
【详解】根据积的变化规律知:一个因数不变,另一个因数扩大或缩小几倍(0除外),积也扩大或缩小几倍,所以一个三角形的底扩大到原来的2倍,高不变,面积就扩大到原来的2倍;21·cn·jy·com
【点睛】本题主要考查了学生根据三角形的面积公式和积的变化规律解答问题的能力。
7.B
【解析】略
8.A
【分析】
如图,等底等高的两个三角形面积相等,因此三角形ACD的面积=三角形BCD的面积,同时减去下边空白部分的面积,剩下的面积依然相等,据此分析。
【详解】根据分析,三角形甲的面积+下边空白三角形=三角形乙的面积+下边空白三角形,根据等式的性质1,两边同时减去下边空白三角形,可得三角形甲的面积=三角形乙的面积。
故答案为:A
9.B
【分析】由题意可知,空白三角形与平行四边形等底等高,则空白三角形的面积等于平行四边形的面积的一半,即阴影部分的面积等于平行四边形的面积的一半,据此计算并选择即可。
【详解】10÷2=5(cm2)
则阴影部分的面积是5cm2。
故答案为:B
10.C
【分析】根据三角形的面积公式:S=ah÷2,即ah=2S,再结合积不变的规律,一个因数乘几或除以几(0除外),另一个因数除以几或乘几,积不变。据此解答即可。
【详解】一个三角形如果高扩大到原来的6倍,要使面积不变,这条高对应的底应该缩小到原来的。
故答案为:C
11.C
【分析】设大正方形的边长为a,小正方形的边长为b,根据三角形的面积公式,分别表示出四个图形中阴影部分的面积,比较即可。www.21-cn-jy.com
【详解】设大正方形的边长为a,小正方形的边长为b。a>b
①的面积:ab÷2;
②的面积:ab÷2;
③的面积:a2÷2
④的面积:b2÷2
由此可以看出四个图形的面积关系是③>①=②>④
故选择:C。
【点睛】此题主要考查了三角形的面积计算,找出三角形对应的底和高是解题关键。
12.B
【分析】在推导三角形面积公式时,把两个完全相同的三角形拼成了一个平行四边形,而拼成的平行四边形与三角形等底等高,平行四边形的面积等于三角形面积的2倍,可得长方形的面积也等于和它等底等高的三角形面积的2倍,据此解答即可。2·1·c·n·j·y
【详解】15×2=30(平方厘米)
这个长方形的面积为30平方厘米。
故答案为:B
【点睛】此题主要考查长方形的面积公式、等底等高的三角形与长方形面积之间的关系及应用。
13.C
【详解】阴影部分和空白部分的面积都是平行四边形面积的一半.
14.×
【分析】根据三角形的特征,任何三角形都有三条边、三个顶点、三个角、三条高;轴对称图形的定义:一个图形沿某条直线对折,直线两旁的部分能够完全重合,这个图形就是轴对称图形,这条直线就是这个图形的一条对称轴,据此解答。【来源:21·世纪·教育·网】
【详解】根据三角形的特征可知,每个三角形都有三条高、三个顶点、三条边;但只有等腰三角形、等边三角形是轴对称图形,其他的三角形不是轴对称图形;所以原题说法错误。
故答案为:×
【点睛】解答此题应根据三角形的特点及分类进行解答。
15.×
【分析】根据三角形的面积公式:底×高÷2,平行四边形的面积公式:底×高,所以如果一个三角形与一个平行四边形的面积相等,底相等,那么三角形的高是平行四边形的2倍。
【详解】一个三角形与一个平行四边形的面积相等,底相等,那么三角形的高是平行四边形的2倍。所以原题说法错误。www-2-1-cnjy-com
故答案为:×
【点睛】此题考查了三角形的面积公式以及平行四边形的面积公式。
16.×
【解析】略
17.×
【分析】根据公式:平行四边形的面积=底×高、三角形的面积=底×高÷2,计算出两个图形的面积,再进行大小比较,即可解答。2-1-c-n-j-y
【详解】平行四边形的面积:
3×1=3(平方厘米)
3×1÷2=1.5(平方厘米)
3≠1.5
故答案为:×
18.√
【分析】从图中可知图形是三角形,根据三角形面积公式:面积=底×高÷2,以及积的变化规律:如果一个因数扩大若干倍,另一个因数不变,那么积也扩大相同倍数,进行判断即可。
【详解】由分析可得:
从三角形面积公式中,可知2是一个固定值,底不变,另一个因数高变大,则乘积就变大,所以三角形的底不变,高越大,面积越大。21*cnjy*com
故答案为:√
【点睛】本题考查了三角形面积公式和积的变化规律,需要学生熟练掌握积和因数之间的变化关系。
19.9分米
【分析】根据三角形的面积公式:S=ah÷2,那么a=2S÷h,把数据代入公式解答。
【详解】35.1×2÷7.8
=70.2÷7.8
=9(分米)
答:这个高对应的底是9分米。
【点睛】此题主要考查三角形面积公式的灵活运用,关键是熟记公式。
20.18厘米、24厘米、30厘米
【详解】试题分析:根据题意,先求出总份数,再分别求出最短的边和最长的边各占周长的几分之几,然后根据一个数乘分数的意义解答.【来源:21cnj*y.co*m】
解:总份数:3+4+5=12(份),
72×=18(厘米),
72×=24(厘米),
72×=30(厘米),
答:三角形三条边的长度分别是18厘米、24厘米、30厘米.
点评:此题考查的目的是使学生掌握按比例分配应用题的结构特征和解答规律,已知两个数的比(三个数的比),两个数的和(三个数的和),求这两个数(三个数),先求出总份数,再求出各部分占总数的几分之几,然后根据一个数乘分数的意义,用乘法解答.
21.(1)玫瑰园占地1500,种玫瑰一共需要7500元.(2)答案不唯一
【详解】(1)75×40÷2=1500()
1500×5=7500(元)
答:玫瑰园占地1500,种玫瑰一共需要7500元.
(2)牡丹园占地多少平方米?
40×40÷2=800()
答:牡丹园占地800.(答案不唯一)
22.96块
【分析】正方形的面积=边长×边长,三角形的面积=底×高÷2,代入数据分别求出客厅与瓷砖的面积,再用客厅的面积÷瓷砖的面积即可。21cnjy.com
【详解】(2.4×2.4)÷(0.6×0.2÷2)
=5.76÷0.06
=96(块)
答:需要96块这种瓷砖。
【点睛】本题主要考查三角形面积公式的实际应用。
23.8米
【分析】根据三角形的面积公式:S=ah÷2,那么h=2S÷a,把数据代入公式解答。
【详解】60×2÷15
=120÷15
=8(米)
答:另一个直角边长8米。
【点睛】此题主要考查三角形面积公式的灵活运用,关键是熟记公式。
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
4.4探索活动:三角形的面积
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.以正方形的4个顶点和正方形的中心(共5个点)为顶点,可以套出 种面积不等的三角形.
2.一个三角形,底为6分米,高为30厘米,它的面积是 .
3.如图中图 的面积与图①相等.
如图,平行四边形的面积是18平方分米,阴影部分两个三角形的面积是 .
如图:三条直线互相平行,l1与l3之间的距离是7厘米,l2上AB=4厘米.求阴影部分三角形的面积是 .
21·世纪*教育网
6.把一个三角形的底扩大到原来的2倍,高不变,面积就扩大到原来的 倍。
二、选择题
7.一个三角形的高是5cm,高对应的底增加8 cm,面积增加( )。
A.8 B.20 C.40 D.无法确定
8.如图,在等腰梯形中三角形甲的面积( )三角形乙的面积。
A.= B.> C.< D.无法确定
9.如图,已知平行四边形的面积是10cm2,则阴影部分的面积是( )。
A.4cm2 B.5cm2 C.3.75cm2 D.2.5cm2
10.一个三角形如果高扩大到原来的6倍,要使面积不变,这条高对应的底应该( )。
A.不变 B.扩大到原来的6倍 C.缩小到原来的 D.缩小到原来的
11.如图是用大小两个正方形组成的组合图形,比较涂色部分的面积,说法错误的是( )。
A.①和②的面积相等 B.②比③的面积小
C.③和④的面积相等 D.④的面积最小
12.如下图,在长方形中,如果红色部分的面积为15平方厘米,则这个长方形的面积为( )。
A.15平方厘米 B.30平方厘米
C.20平方厘米 D.无法判断
13.下图中阴影部分的面积和空白部分的面积的关系是( ).
A.阴影部分的面积大 B.空白部分的面积大
C.两部分面积相等 D.无法确定
三、判断题
14.每个三角形都有三条高、三个顶点、三条边和三条对称轴。( )
15.一个三角形和一个平行四边形面积相等,底相等,高也一定相等。( )
16.平行四边形的面积等于三角形面积. ( )
17.图形和的面积相等。( )
18.如图,这个三角形的底不变,高越大,面积越大。( )
四、解答题
19.一块三角形交通标志牌,面积是35.1dm2,高是7.8dm,这个高对应的底是多少分米?
20.一个三角形三边的长度比是3:4:5.这个三角形的周长是72厘米,三边的长度分别是多少厘米?
21.公园里有两块空地,计划分别种玫瑰和牡丹.
占地面积 价格
玫瑰 每棵占地 每棵5元
牡丹 每棵占地 每棵12元
(1)玫瑰园占地多少平方米?种玫瑰一共需要多少元?
(2)你还能提出什么数学问题?并尝试解答.
22.有一个边长是2.4m正方形客厅,用三角形瓷砖(如图)铺满,需要多少块这种瓷砖?
23.如图,一个直角三角形花坛的面积是60平方米,一条直角边长15米,另一条直角边长多少米?
参考答案:
1.2
【详解】试题分析:要求可以套出几种面积不等的三角形,可分两种情况进行分析:(1)如果三个顶点全取正方形顶点,三角形面积和正方形面积的关系;(2)如果一个顶点取在正方形的中心,另两个点取正方形的顶点,三角形的面积和正方形面积的关系;
解:(1)如果三个顶点全取正方形顶点,则无论怎样套,三角形面积都是正方形面积的一半;
(2)如果一个顶点取在正方形的中心,则无论怎样套,三角形的面积都是正方形面积的;
所以面积不同的三角形共有2种.
答:可以套出2种面积不等的三角形;
故答案为2.
点评:解答此题的关键是先进行假设,进而通过假设得到的数据进行比较,进而得出结论.
2.9平方分米
【详解】试题分析:三角形的面积S=ah,据此代入数据即可求解.
解:30厘米=3分米,
6×3÷2=9(平方分米);
答:这个三角形的面积是9平方分米.
故答案为9平方分米.
点评:此题主要考查三角形的面积的计算方法的灵活应用.
3.③⑦
【详解】试题分析:根据长方形的面积=长×宽,梯形的面积=(上底+下底)×高÷2,正方形的面积=边长×边长,三角形的面积=底×高÷2,平行四边形的面积=底×高,以及利用图形的割补法求出图形⑦,是一个长5、宽3的长方形的面积,再与图形①的面积相比较即可解答问题.21教育网
解:图形①的面积是:3×5=15;
图形②的面积是:(5+2)×3÷2,
=7×3÷2,
=10.5;
图形③的面积是:(4+2)×5÷2,
=6×5÷2,
=15;
图形④的面积是:3×4=12;
图形⑤的面积是:4×4=16;
图形⑥的面积是:4×5÷2,
=20÷2,
=10;
图形⑦的面积是:3×5=15;
图形⑧的面积是:3×4=12.
所以与图形①的面积相等的是图形③和⑦.
故答案为③⑦.
点评:此题主要考查几种常见图形的面积公式的计算应用,熟记公式即可解答.
4.9平方分米
【详解】试题分析:由题意得:阴影部分面积=平行四边形的面积﹣空白三角形面积,空白三角形与平行四边形等底等高,所以空白三角形面积=平行四边形的面积÷2,代数计算即可.
解:18﹣18÷2,
=18﹣9,
=9(平方分米).
答:阴影部分两个三角形的面积是9平方分米.
故答案为9平方分米.
点评:解决本题的关键是明确空白三角形与平行四边形等底等高,所以空白三角形面积=平行四边形的面积÷2.21世纪教育网版权所有
5.14平方厘米
【详解】试题分析:
如上图,阴影部分的面积等于上面三角形△ABC的面积加上下面三角形△ABD的面积,假设l1和l2间的距离是h1,l2和l3间的距离是h2,根据三角形的面积公式,列出等式,都有底AB,提取公因数AB,h1+h2就是l1和l3间的距离7厘米,因此得解.
解:S△ABC+S△ABD=AB h1+AB h2=AB (h1+h2)=×4×7=14(平方厘米);
答:阴影部分三角形的面积是14平方厘米.
故答案为14平方厘米.
点评:此题的关键是面积之和,提取公因数,刚好和已知联系起来.
6.2
【分析】根据三角形的面积公式:S=ah和积的变化规律进行解答即可。
【详解】根据积的变化规律知:一个因数不变,另一个因数扩大或缩小几倍(0除外),积也扩大或缩小几倍,所以一个三角形的底扩大到原来的2倍,高不变,面积就扩大到原来的2倍;21·cn·jy·com
【点睛】本题主要考查了学生根据三角形的面积公式和积的变化规律解答问题的能力。
7.B
【解析】略
8.A
【分析】
如图,等底等高的两个三角形面积相等,因此三角形ACD的面积=三角形BCD的面积,同时减去下边空白部分的面积,剩下的面积依然相等,据此分析。
【详解】根据分析,三角形甲的面积+下边空白三角形=三角形乙的面积+下边空白三角形,根据等式的性质1,两边同时减去下边空白三角形,可得三角形甲的面积=三角形乙的面积。
故答案为:A
9.B
【分析】由题意可知,空白三角形与平行四边形等底等高,则空白三角形的面积等于平行四边形的面积的一半,即阴影部分的面积等于平行四边形的面积的一半,据此计算并选择即可。
【详解】10÷2=5(cm2)
则阴影部分的面积是5cm2。
故答案为:B
10.C
【分析】根据三角形的面积公式:S=ah÷2,即ah=2S,再结合积不变的规律,一个因数乘几或除以几(0除外),另一个因数除以几或乘几,积不变。据此解答即可。
【详解】一个三角形如果高扩大到原来的6倍,要使面积不变,这条高对应的底应该缩小到原来的。
故答案为:C
11.C
【分析】设大正方形的边长为a,小正方形的边长为b,根据三角形的面积公式,分别表示出四个图形中阴影部分的面积,比较即可。www.21-cn-jy.com
【详解】设大正方形的边长为a,小正方形的边长为b。a>b
①的面积:ab÷2;
②的面积:ab÷2;
③的面积:a2÷2
④的面积:b2÷2
由此可以看出四个图形的面积关系是③>①=②>④
故选择:C。
【点睛】此题主要考查了三角形的面积计算,找出三角形对应的底和高是解题关键。
12.B
【分析】在推导三角形面积公式时,把两个完全相同的三角形拼成了一个平行四边形,而拼成的平行四边形与三角形等底等高,平行四边形的面积等于三角形面积的2倍,可得长方形的面积也等于和它等底等高的三角形面积的2倍,据此解答即可。2·1·c·n·j·y
【详解】15×2=30(平方厘米)
这个长方形的面积为30平方厘米。
故答案为:B
【点睛】此题主要考查长方形的面积公式、等底等高的三角形与长方形面积之间的关系及应用。
13.C
【详解】阴影部分和空白部分的面积都是平行四边形面积的一半.
14.×
【分析】根据三角形的特征,任何三角形都有三条边、三个顶点、三个角、三条高;轴对称图形的定义:一个图形沿某条直线对折,直线两旁的部分能够完全重合,这个图形就是轴对称图形,这条直线就是这个图形的一条对称轴,据此解答。【来源:21·世纪·教育·网】
【详解】根据三角形的特征可知,每个三角形都有三条高、三个顶点、三条边;但只有等腰三角形、等边三角形是轴对称图形,其他的三角形不是轴对称图形;所以原题说法错误。
故答案为:×
【点睛】解答此题应根据三角形的特点及分类进行解答。
15.×
【分析】根据三角形的面积公式:底×高÷2,平行四边形的面积公式:底×高,所以如果一个三角形与一个平行四边形的面积相等,底相等,那么三角形的高是平行四边形的2倍。
【详解】一个三角形与一个平行四边形的面积相等,底相等,那么三角形的高是平行四边形的2倍。所以原题说法错误。www-2-1-cnjy-com
故答案为:×
【点睛】此题考查了三角形的面积公式以及平行四边形的面积公式。
16.×
【解析】略
17.×
【分析】根据公式:平行四边形的面积=底×高、三角形的面积=底×高÷2,计算出两个图形的面积,再进行大小比较,即可解答。2-1-c-n-j-y
【详解】平行四边形的面积:
3×1=3(平方厘米)
3×1÷2=1.5(平方厘米)
3≠1.5
故答案为:×
18.√
【分析】从图中可知图形是三角形,根据三角形面积公式:面积=底×高÷2,以及积的变化规律:如果一个因数扩大若干倍,另一个因数不变,那么积也扩大相同倍数,进行判断即可。
【详解】由分析可得:
从三角形面积公式中,可知2是一个固定值,底不变,另一个因数高变大,则乘积就变大,所以三角形的底不变,高越大,面积越大。21*cnjy*com
故答案为:√
【点睛】本题考查了三角形面积公式和积的变化规律,需要学生熟练掌握积和因数之间的变化关系。
19.9分米
【分析】根据三角形的面积公式:S=ah÷2,那么a=2S÷h,把数据代入公式解答。
【详解】35.1×2÷7.8
=70.2÷7.8
=9(分米)
答:这个高对应的底是9分米。
【点睛】此题主要考查三角形面积公式的灵活运用,关键是熟记公式。
20.18厘米、24厘米、30厘米
【详解】试题分析:根据题意,先求出总份数,再分别求出最短的边和最长的边各占周长的几分之几,然后根据一个数乘分数的意义解答.【来源:21cnj*y.co*m】
解:总份数:3+4+5=12(份),
72×=18(厘米),
72×=24(厘米),
72×=30(厘米),
答:三角形三条边的长度分别是18厘米、24厘米、30厘米.
点评:此题考查的目的是使学生掌握按比例分配应用题的结构特征和解答规律,已知两个数的比(三个数的比),两个数的和(三个数的和),求这两个数(三个数),先求出总份数,再求出各部分占总数的几分之几,然后根据一个数乘分数的意义,用乘法解答.
21.(1)玫瑰园占地1500,种玫瑰一共需要7500元.(2)答案不唯一
【详解】(1)75×40÷2=1500()
1500×5=7500(元)
答:玫瑰园占地1500,种玫瑰一共需要7500元.
(2)牡丹园占地多少平方米?
40×40÷2=800()
答:牡丹园占地800.(答案不唯一)
22.96块
【分析】正方形的面积=边长×边长,三角形的面积=底×高÷2,代入数据分别求出客厅与瓷砖的面积,再用客厅的面积÷瓷砖的面积即可。21cnjy.com
【详解】(2.4×2.4)÷(0.6×0.2÷2)
=5.76÷0.06
=96(块)
答:需要96块这种瓷砖。
【点睛】本题主要考查三角形面积公式的实际应用。
23.8米
【分析】根据三角形的面积公式:S=ah÷2,那么h=2S÷a,把数据代入公式解答。
【详解】60×2÷15
=120÷15
=8(米)
答:另一个直角边长8米。
【点睛】此题主要考查三角形面积公式的灵活运用,关键是熟记公式。
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
