人教版六年级下册数学 数学思考(第3课时)课件(共23张PPT)
文档属性
| 名称 | 人教版六年级下册数学 数学思考(第3课时)课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 11.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-09 11:48:07 | ||
图片预览






文档简介
(共23张PPT)
数学思考(第三课时)
说说什么是推理?
推导的过程……
从已知的条件出发……分析……得到结论……
列表推理和排除法……
说说什么是推理?
推导的过程……
从已知的条件出发……分析……得到结论……
列表推理和排除法……
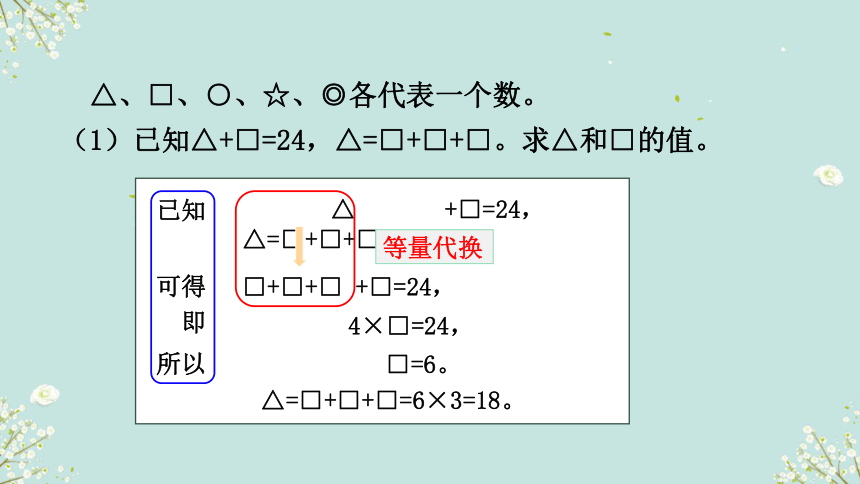
△、□、○、☆、◎各代表一个数。
(1)已知△+□=24,△=□+□+□。求△和□的值。
1
△、□、○、☆、◎各代表一个数。
(1)已知△+□=24,△=□+□+□。求△和□的值。
1
△=□+□+□
△、□、○、☆、◎各代表一个数。
(1)已知△+□=24,△=□+□+□。求△和□的值。
□+□+□+□=24
4×□=24
□=6
△=□+□+□=6×3=18
△+□=24
□+□+□+□=24,
4×□=24,
□=6。
△=□+□+□=6×3=18。
△+□=24,△=□+□+□,
已知
可得
即
所以
△、□、○、☆、◎各代表一个数。
(1)已知△+□=24,△=□+□+□。求△和□的值。
□+□+□ +□=24,
4×□=24,
□=6。
△=□+□+□=6×3=18。
△ +□=24,△=□+□+□,
已知
可得
即
所以
等量代换
△、□、○、☆、◎各代表一个数。
(2)已知○+☆=160,◎+☆=160。○是否等于◎?
△、□、○、☆、◎各代表一个数。
(2)已知○+☆=160,◎+☆=160。○是否等于◎?
共同量。
等式的性质1
等式两边加上或减去同一个数,左右两边仍然相等。
等式的性质2
等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
△、□、○、☆、◎各代表一个数。
(2)已知○+☆=160,◎+☆=160。○是否等于◎?
已知,○+☆=160,◎+☆=160,
根据等式的性质,等式两边都减去☆,
可以推出○=160-☆,◎=160 -☆。
因为☆代表同一个数,所以○=◎。
已知,○+☆=160,◎+☆=160,
可以推出,○+☆=◎+☆。
可以得到 ○=◎。
因为☆代表同一个数,根据等式的性质,
△、□、○、☆、◎各代表一个数。
(2)已知○+☆=160,◎+☆=160。○是否等于◎?
等式两边都减去☆,
等式的传递性:
若a=b,b=c,则a=c。
等量代换
等式的性质
(2)已知○+☆=160,◎+☆=160。○是否等于◎?
(1)已知△+□=24,△=□+□+□。求△和□的值。
数学证明方法
2
什么是平角?平角与直线有什么区别?
180°
1平角=180°
平角
直线
两端可以无限延长,没有端点。
平角的两条边在同一直线上。
如右图,两条直线相交于点O。
(1)每相邻两个角可以组成一个平角,一共能组成几个平角?
∠4和∠1
平角的两边在一条直线上。
(根据概念推理)
∠1和∠2
∠2和∠3
∠3和∠4
一共能组成4个平角。
如右图,两条直线相交于点O。
(2)你能推出∠1=∠3吗?
∠1和∠2,∠2和∠3都能组成平角,可以把相等的关系用等式表示出来。
与推理○和◎的关系相似。
根据第(1)题的结论,
可以得到 ∠1+∠2=180°,
∠2+∠3=180°。
根据等式的性质,等式的两边都减去∠2,
可以得到 ∠1=180°-∠2,
∠3=180°-∠2。
因为 180°-∠2=180°-∠2,
所以 ∠1=∠3。
如何才能有理有据的说理证明呢?
等量代换
等式的性质
等式的传递性
数学概念
《几何原本》是古希腊数学家欧几里得所著的一部数学著作。所记载的第一条公理就是“等于同量的量彼此相等”。
数学推理语言:
准确,简洁,清晰,严谨。
如图,把三角形ABC的边BC延长到点D。
(1)∠3 和∠4 拼成的是什么角?
(2)你能说明∠1+∠2=∠4吗?
3
由第(1)小题中的结论,可得∠3+∠4 =180°;
根据三角形内角和是180°,可知∠1+∠2 +∠3 =180°;
可得,∠3+∠4 =∠1+∠2 +∠3。
根据等式的性质,等式的两边都减去∠3,
可以得到 ∠4 =∠1+∠2,
即 ∠1+∠2 =∠4。
平角
数学思考
同学们再见!
数学思考(第三课时)
说说什么是推理?
推导的过程……
从已知的条件出发……分析……得到结论……
列表推理和排除法……
说说什么是推理?
推导的过程……
从已知的条件出发……分析……得到结论……
列表推理和排除法……
△、□、○、☆、◎各代表一个数。
(1)已知△+□=24,△=□+□+□。求△和□的值。
1
△、□、○、☆、◎各代表一个数。
(1)已知△+□=24,△=□+□+□。求△和□的值。
1
△=□+□+□
△、□、○、☆、◎各代表一个数。
(1)已知△+□=24,△=□+□+□。求△和□的值。
□+□+□+□=24
4×□=24
□=6
△=□+□+□=6×3=18
△+□=24
□+□+□+□=24,
4×□=24,
□=6。
△=□+□+□=6×3=18。
△+□=24,△=□+□+□,
已知
可得
即
所以
△、□、○、☆、◎各代表一个数。
(1)已知△+□=24,△=□+□+□。求△和□的值。
□+□+□ +□=24,
4×□=24,
□=6。
△=□+□+□=6×3=18。
△ +□=24,△=□+□+□,
已知
可得
即
所以
等量代换
△、□、○、☆、◎各代表一个数。
(2)已知○+☆=160,◎+☆=160。○是否等于◎?
△、□、○、☆、◎各代表一个数。
(2)已知○+☆=160,◎+☆=160。○是否等于◎?
共同量。
等式的性质1
等式两边加上或减去同一个数,左右两边仍然相等。
等式的性质2
等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
△、□、○、☆、◎各代表一个数。
(2)已知○+☆=160,◎+☆=160。○是否等于◎?
已知,○+☆=160,◎+☆=160,
根据等式的性质,等式两边都减去☆,
可以推出○=160-☆,◎=160 -☆。
因为☆代表同一个数,所以○=◎。
已知,○+☆=160,◎+☆=160,
可以推出,○+☆=◎+☆。
可以得到 ○=◎。
因为☆代表同一个数,根据等式的性质,
△、□、○、☆、◎各代表一个数。
(2)已知○+☆=160,◎+☆=160。○是否等于◎?
等式两边都减去☆,
等式的传递性:
若a=b,b=c,则a=c。
等量代换
等式的性质
(2)已知○+☆=160,◎+☆=160。○是否等于◎?
(1)已知△+□=24,△=□+□+□。求△和□的值。
数学证明方法
2
什么是平角?平角与直线有什么区别?
180°
1平角=180°
平角
直线
两端可以无限延长,没有端点。
平角的两条边在同一直线上。
如右图,两条直线相交于点O。
(1)每相邻两个角可以组成一个平角,一共能组成几个平角?
∠4和∠1
平角的两边在一条直线上。
(根据概念推理)
∠1和∠2
∠2和∠3
∠3和∠4
一共能组成4个平角。
如右图,两条直线相交于点O。
(2)你能推出∠1=∠3吗?
∠1和∠2,∠2和∠3都能组成平角,可以把相等的关系用等式表示出来。
与推理○和◎的关系相似。
根据第(1)题的结论,
可以得到 ∠1+∠2=180°,
∠2+∠3=180°。
根据等式的性质,等式的两边都减去∠2,
可以得到 ∠1=180°-∠2,
∠3=180°-∠2。
因为 180°-∠2=180°-∠2,
所以 ∠1=∠3。
如何才能有理有据的说理证明呢?
等量代换
等式的性质
等式的传递性
数学概念
《几何原本》是古希腊数学家欧几里得所著的一部数学著作。所记载的第一条公理就是“等于同量的量彼此相等”。
数学推理语言:
准确,简洁,清晰,严谨。
如图,把三角形ABC的边BC延长到点D。
(1)∠3 和∠4 拼成的是什么角?
(2)你能说明∠1+∠2=∠4吗?
3
由第(1)小题中的结论,可得∠3+∠4 =180°;
根据三角形内角和是180°,可知∠1+∠2 +∠3 =180°;
可得,∠3+∠4 =∠1+∠2 +∠3。
根据等式的性质,等式的两边都减去∠3,
可以得到 ∠4 =∠1+∠2,
即 ∠1+∠2 =∠4。
平角
数学思考
同学们再见!
