12.2 三角形全等的判断 同步训练(含简单答案) 2024-2025学年人教版数学八年级上册(1)
文档属性
| 名称 | 12.2 三角形全等的判断 同步训练(含简单答案) 2024-2025学年人教版数学八年级上册(1) |
|
|
| 格式 | docx | ||
| 文件大小 | 359.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-09 18:36:10 | ||
图片预览


文档简介
12.2 三角形全等的判断 同步训练 2024-2025学年人教版数学八年级上册(1)
一、单选题
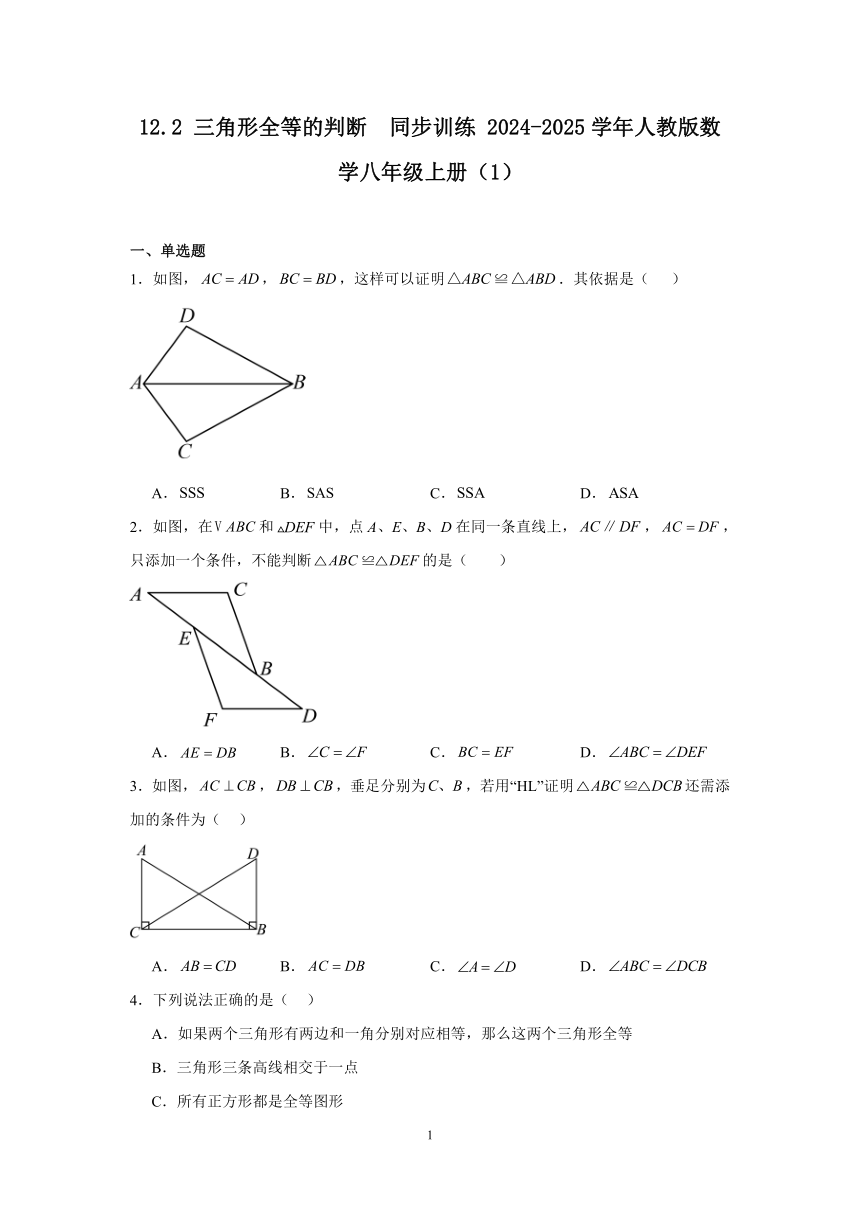
1.如图,,,这样可以证明.其依据是( )
A. B. C. D.
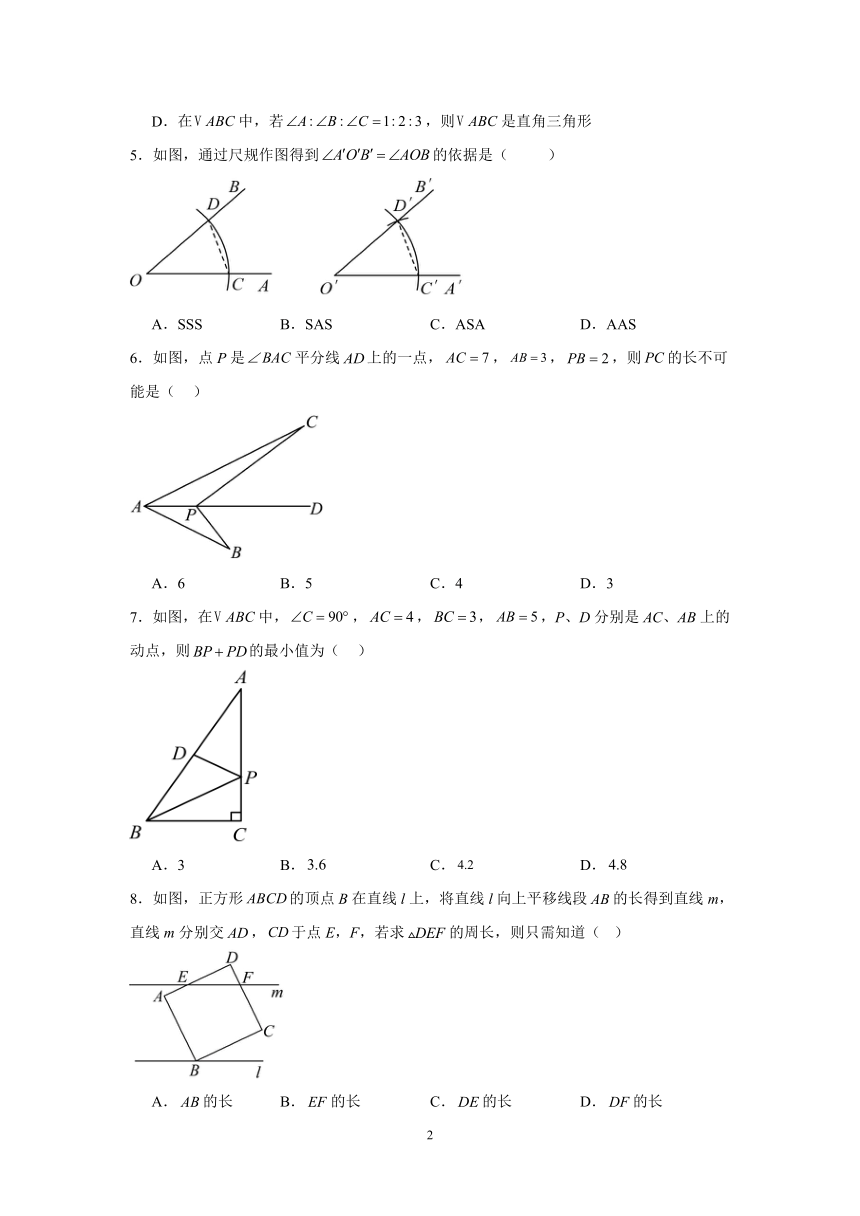
2.如图,在和中,点A、E、B、D在同一条直线上,,,只添加一个条件,不能判断的是( )
A. B. C. D.
3.如图,,,垂足分别为,若用“HL”证明还需添加的条件为( )
A. B. C. D.
4.下列说法正确的是( )
A.如果两个三角形有两边和一角分别对应相等,那么这两个三角形全等
B.三角形三条高线相交于一点
C.所有正方形都是全等图形
D.在中,若,则是直角三角形
5.如图,通过尺规作图得到的依据是( )
A.SSS B.SAS C.ASA D.AAS
6.如图,点P是平分线上的一点,,,,则的长不可能是( )
A.6 B.5 C.4 D.3
7.如图,在中,,,,,P、D分别是AC、AB上的动点,则的最小值为( )
A.3 B. C. D.
8.如图,正方形的顶点B在直线l上,将直线l向上平移线段的长得到直线m,直线m分别交,于点E,F,若求的周长,则只需知道( )
A.的长 B.的长 C.的长 D.的长
9.勾股定理被誉为“几何明珠”.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图所示,把一个边长分别为3,4,5的三角形和三个正方形放置在大长方形中,则该长方形中空白部分的面积为( )
A.54 B.60 C.100 D.110
10.如图,小丽在公园里荡秋千,她坐在秋千的起始位置处,与地面垂直,当她荡到距地面高的处时,与的水平距离为,当她荡到与的水平距离为的处,,此时小丽距离地面的高度是( )
A. B. C. D.
二、填空题
11.斜边和一条 分别对应相等的两个直角三角形全等(可以简写成“ ”或“ ”).
12.如图,,,要使,则可添加的一个条件是 (写出一个即可).
13.如图,,,则图中全等三角形有 对.
14.如图直角三角形中的空白部分是正方形,正方形的一个顶点将这个直角三角形的斜边分成二部分,AD=3厘米,阴影部分的面积是6平方厘米,长 厘米.
三、解答题
15.如图,已知,用直尺和圆规在射线的右侧作,使得.(不写作法,只需保留作图痕迹)
16.两个大小不同的等腰直角三角板按如图①所示方式放置,图②是由图①抽象出的几何图形,其中,,,点B、C、E在同一条直线上.连接.求证:.
17.如图,在Rt△ABC中,∠C=90°,AC=BC,△ABC绕点B顺时针旋转45°得到△BDE,点D的对应点为点A,连接AD,求∠ADE的度数.
18.如图,AE,BD相交于点C,,,cm,点P从点A出发,沿A→B→A方向以3cm/s的速度匀速运动,点Q从点D出发,沿D→E方向以1cm/s的速度匀速运动.P,Q两点同时出发,当点P回到点A时,P,Q两点同时停止运动.设点P的运动时间为t(s).
(1)当s时,______cm,当s时,______cm.
(2)求证:.
参考答案:
1.A
2.C
3.A
4.D
5.A
6.A
7.D
8.A
9.B
10.A
11. 直角边 斜边、直角边
12.(答案不唯一)
13.6
14.4
15.
16.
17.22.5°
18.(1)3,2
(2)
一、单选题
1.如图,,,这样可以证明.其依据是( )
A. B. C. D.
2.如图,在和中,点A、E、B、D在同一条直线上,,,只添加一个条件,不能判断的是( )
A. B. C. D.
3.如图,,,垂足分别为,若用“HL”证明还需添加的条件为( )
A. B. C. D.
4.下列说法正确的是( )
A.如果两个三角形有两边和一角分别对应相等,那么这两个三角形全等
B.三角形三条高线相交于一点
C.所有正方形都是全等图形
D.在中,若,则是直角三角形
5.如图,通过尺规作图得到的依据是( )
A.SSS B.SAS C.ASA D.AAS
6.如图,点P是平分线上的一点,,,,则的长不可能是( )
A.6 B.5 C.4 D.3
7.如图,在中,,,,,P、D分别是AC、AB上的动点,则的最小值为( )
A.3 B. C. D.
8.如图,正方形的顶点B在直线l上,将直线l向上平移线段的长得到直线m,直线m分别交,于点E,F,若求的周长,则只需知道( )
A.的长 B.的长 C.的长 D.的长
9.勾股定理被誉为“几何明珠”.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图所示,把一个边长分别为3,4,5的三角形和三个正方形放置在大长方形中,则该长方形中空白部分的面积为( )
A.54 B.60 C.100 D.110
10.如图,小丽在公园里荡秋千,她坐在秋千的起始位置处,与地面垂直,当她荡到距地面高的处时,与的水平距离为,当她荡到与的水平距离为的处,,此时小丽距离地面的高度是( )
A. B. C. D.
二、填空题
11.斜边和一条 分别对应相等的两个直角三角形全等(可以简写成“ ”或“ ”).
12.如图,,,要使,则可添加的一个条件是 (写出一个即可).
13.如图,,,则图中全等三角形有 对.
14.如图直角三角形中的空白部分是正方形,正方形的一个顶点将这个直角三角形的斜边分成二部分,AD=3厘米,阴影部分的面积是6平方厘米,长 厘米.
三、解答题
15.如图,已知,用直尺和圆规在射线的右侧作,使得.(不写作法,只需保留作图痕迹)
16.两个大小不同的等腰直角三角板按如图①所示方式放置,图②是由图①抽象出的几何图形,其中,,,点B、C、E在同一条直线上.连接.求证:.
17.如图,在Rt△ABC中,∠C=90°,AC=BC,△ABC绕点B顺时针旋转45°得到△BDE,点D的对应点为点A,连接AD,求∠ADE的度数.
18.如图,AE,BD相交于点C,,,cm,点P从点A出发,沿A→B→A方向以3cm/s的速度匀速运动,点Q从点D出发,沿D→E方向以1cm/s的速度匀速运动.P,Q两点同时出发,当点P回到点A时,P,Q两点同时停止运动.设点P的运动时间为t(s).
(1)当s时,______cm,当s时,______cm.
(2)求证:.
参考答案:
1.A
2.C
3.A
4.D
5.A
6.A
7.D
8.A
9.B
10.A
11. 直角边 斜边、直角边
12.(答案不唯一)
13.6
14.4
15.
16.
17.22.5°
18.(1)3,2
(2)
