3.4 力的合成和分解课件—2024-2025学年高一上学期物理人教版(2019)必修第一册(共29张PPT)
文档属性
| 名称 | 3.4 力的合成和分解课件—2024-2025学年高一上学期物理人教版(2019)必修第一册(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-08-09 21:33:48 | ||
图片预览







文档简介
(共29张PPT)
第三章
相互作用——力
3.4 力的合成和分解
目录
一、上节回溯
三、小结
四、练习
二、知识讲解
1.作用力和反作用力
2.牛顿第三定律
3.受力分析
一、上节回溯
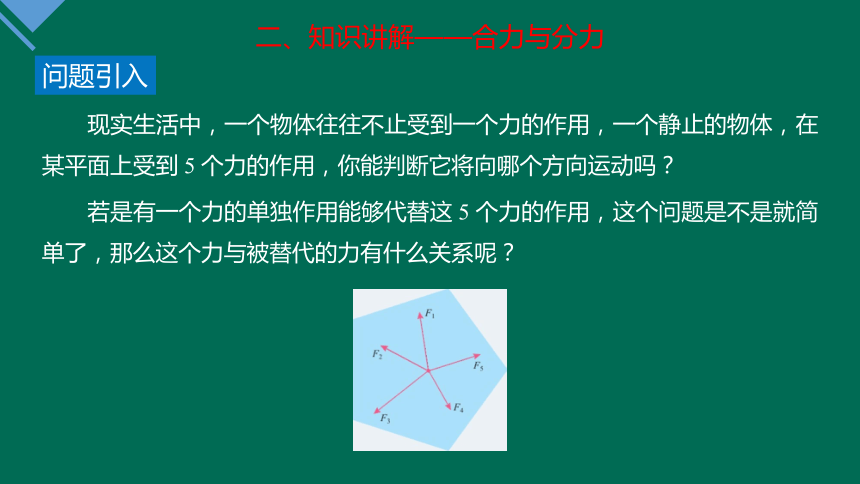
现实生活中,一个物体往往不止受到一个力的作用,一个静止的物体,在某平面上受到 5 个力的作用,你能判断它将向哪个方向运动吗?
若是有一个力的单独作用能够代替这 5 个力的作用,这个问题是不是就简单了,那么这个力与被替代的力有什么关系呢?
问题引入
二、知识讲解——合力与分力
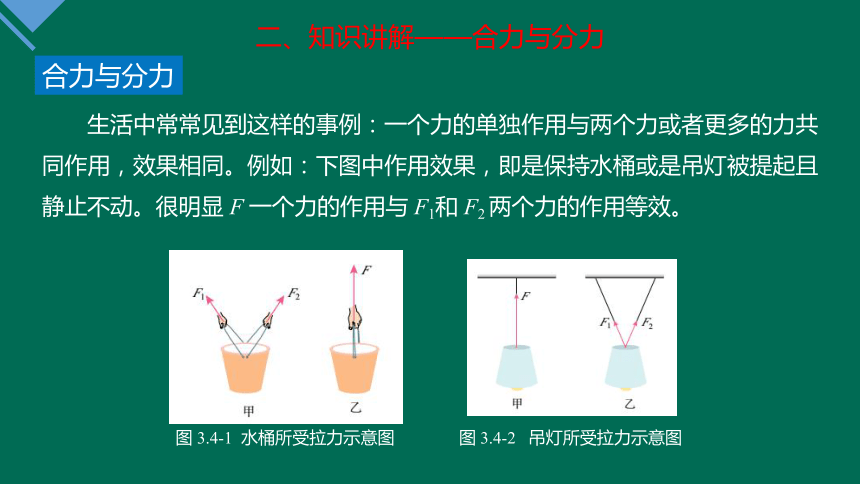
生活中常常见到这样的事例:一个力的单独作用与两个力或者更多的力共同作用,效果相同。例如:下图中作用效果,即是保持水桶或是吊灯被提起且静止不动。很明显 F 一个力的作用与 F1和 F2 两个力的作用等效。
合力与分力
图 3.4-1 水桶所受拉力示意图
图 3.4-2 吊灯所受拉力示意图
二、知识讲解——合力与分力
定义:假设一个力单独作用的效果跟某几个力共同作用的效果相同,这个力就叫作那几个力的合力。假设几个力共同作用的效果跟某个力单独作用的效果相同,这几个力就叫作那个力的分力。
合力与分力
分力
合力
等效替代
F
F1、F2、F3…
二、知识讲解——合力与分力
1.力的合成:求几个力的合力的过程;
2.力的分解:求一个力的分力的过程。
力的合成和分解
分力
合力
等效替代
F
F1、F2、F3…
力的合成
力的分解
二、知识讲解——力的合成和分解
如果两个力在同一条直线上,如何求它们的合力?
如果两个力的方向不在同一条直线上,如何求它们的合力?
互成角度的两个力与它们的合力之间有什么关系呢?
思考
二、知识讲解——力的合成和分解
实验目的:探究合力 F 与互成角度的两个力 F1、F2 有什么关系。
设计思路:
(1)力的作用效果:使物体发生形变、改变物体运动状态。如何选择?
(2)如何保证力的作用效果相同?
(3)力的大小如何测量?
(4)力的方向如何确定?
(5)如何记录数据?
探究互成角度的力的合成规律
二、知识讲解——力的合成和分解
请阅读课本“实验”栏目下的内容回答下列问题:
1. 实验中需要用到哪些仪器?
2. 如何提供合力与分力?
如何保证合力与分力的作用效果相同?
3. 在实验过程中,需要记录哪些数据?如何记录?
4. 如何处理记录下来的信息?
5. 要使得测量尽可能地精确,需要注意哪些实验操作细节?
探究互成角度的力的合成规律
二、知识讲解——力的合成和分解
演示实验
1
0
2
3
4
5
N
1
0
2
3
4
5
N
1
0
2
3
4
5
N
记录效果
记录方向
二、知识讲解——力的合成和分解
如何保证用两个弹簧秤和一个弹簧秤拉动橡皮筋的力是等效的?
弹簧秤、细绳、橡皮条是否必须与木板平行 ?
两个分力的大小是用绳长表示吗?
如何减小本实验的偶然误差?
两个分力所用的细绳可以用橡皮绳代替吗?
F 与 F′ 谁是理论值,谁是测量值?
回顾实验
二、知识讲解——力的合成和分解
经过多次实验探究我们会发现,求两个力的合成,如果以表示这两个力的有向线段为邻边作平行四边形,这两个邻边之间的对角线就代表合力的大小和方向。这个规律就叫作平行四边形定则。
实验结论
二、知识讲解——力的合成和分解
如图,研究位移时,可以看出人直接沿 AC 的位移与从 A 到 B 再到 C 的位移相同,因此 AC 是两段位移 AB 和 BC 的合位移。因此位移的合成遵从平行四边形定则。
矢量和标量
A
C
B
(1)矢量:既有大小,也有方向,相加遵从平行四边形定则。
(2)标量:只有大小,没有方向,相加遵从算数运算法则。
二、知识讲解——力的合成和分解
讨论:两个分力大小不变,改变分力的夹角,合力的变化。
力的合成
图例 θ F
最大 θ=0° F=F1+F2
0°< θ < 90° F1+F2> F>
θ=90° F=
90°< θ < 180° |F1-F2|最小 θ=180° F=|F1-F2|
F1
F2
F
F2
F1
F
θ
F2
F1
F
θ
F2
F1
F
θ
F1
F2
F
二、知识讲解——力的合成和分解
力的分解也是遵从平行四边形定则的。
思考:已知两个分力(邻边),则合力(对角线)是唯一的。那么已知合力(对角线),求分力(邻边),答案是否唯一呢?
力的分解
F
结论:如果没有其他限制,同一个力可以分解为无数组大小、方向不同的分力。
注意:不能说成按照力的作用效果进行分解,可以说成根据解决问题的需要进行分解。
二、知识讲解——力的合成和分解
1.如图所示,请判断下列说法正确吗?
(1)F1 就是物块对斜面的压力;
(2)F2 就是物块受到的摩擦力。
常见的问题
G
F2
F1
2.两个力 F1 和 F2 之间的夹角为 θ,其合力为 F 。请判断以下说法是否正确,并简述理由。
(1)合力 F 总比分力 F1 和 F2 中的任何一个力都大。
(2)若 F1 和 F2 大小不变,θ 角越小,则合力 F 就越大。
(3)若夹角 θ 不变,F1 大小不变,F2 增大,则合力 F 一定大。
二、知识讲解——力的合成和分解
常见的问题
3.同一个力,约束条件不同,分解出的两个分力大小、方向就可以不同。
G
G
F2
F1
θ
θ
θ
θ
思考:当挡板与斜面间的夹角逐渐增大的过程中,两个压力的大小怎样变化?
F2
F1
二、知识讲解——力的合成和分解
学以致用
我们在练习引体向上时,双手如何更省力?
双手越接近竖直越省力
F = G
二、知识讲解——力的合成和分解
学以致用
例题:静止在倾斜桥面的汽车,其重力为 G,桥面倾角为 α 。把重力沿平行于桥面和垂直于桥面方向分解为 G1 和 G2 ,求这两个分力的大小。
G1
G2
y
x
G
平行于斜面
使物体下滑的分力 G1
垂直于斜面
使物体紧压斜面的分力 G2
G1=G sin
G2=G cos
增大,G1 增大, G2减小
二、知识讲解——力的合成和分解
学以致用
为什么桥梁要修很长的引桥?
减小倾角,使汽车重力沿桥面的分力减小,利于车辆平缓的上下桥面。
二、知识讲解——力的合成和分解
学以致用
劈的剖面是一个等腰三角形,使用劈的时候,在劈背上加力 F,这个力产生两个效果,使劈的两个侧面推压物体,把物体劈开。设劈背的宽度是 d,劈的侧面的长度是 L。试求:F1 和 F2 的大小。
d
F
F1
F2
力的放大
思考:为什么厚度小的斧头更加锋利?
L
二、知识讲解——力的合成和分解
学以致用
资料
斜拉桥的钢索有什么作用?
F4
F2
F
F '
F3
F1
θ
θ
“拽起” 桥面。海河上的保定桥在河内不设桥墩,而是靠斜拉索的拉力“拽起” 桥面。
二、知识讲解——力的合成和分解
学以致用
资料
斜拉桥的桥塔为什么建很高?
F4
F2
F
F '
F3
F1
θ
θ
桥重一定时,桥塔越高,钢索与水平面的夹角越大,钢索上的拉力越小。
二、知识讲解——力的合成和分解
1.合力
2.分力
3.力的合成
4.力的分解
5.平行四边形定则
6.矢量和标量
三、小结
四、练习
1.有两个力,一个是10 N,一个是 2 N,它们的合力可能等于 5 N,10 N,15 N 吗?合力最大值为多少?最小值为多少?
答:两个力的方向同时,即夹角为 0° 合力最大,最大值为 12 N 。两个力的方向相反时,即夹角为 180 ° 合力最小,最小值为 8 N 。在两个力的夹角从0°逐渐增大到180° 时,合力逐渐减小,即合力大小在 8 N 到 12 N 之间 。所以可能为 10 N 不可能为 5 N 或 15 N 。
答:当两个力的合力为零时,一个力向东,大小为 6 N ,则另一个力必定向西,且大小也为 6 N 。向东的力改为向南时,两个力互相垂直,大小相等,所以用有向线段表示这两个力,构成的平行四边形为正四边形。所以合力的大小为6 N ,方向为西偏南 45 ° 的方向。
2.有两个力,它们的合力为 0 。现把其中一个向东的 6 N 的力改为向南(大小不变),它们合力的大小、方向如何?
四、练习
答:可以将 F 按如图所示的方式分解。
由图可知,FA= ,FB= 。
代入数据可得:尖劈对 A 侧的压力为 FA=20 N ,
对B侧的压力为FB= 10 N
3.(2021山东青岛高一上期中)如图所示吗,表面光滑、重力不计的尖劈,插在缝 A、B 之间,尖劈的一个角为 α=30°,在尖劈背上加一压力 F=10 N,则尖劈对 A 的侧压力和对 B 的侧压力分别为多大?
F
A
B
α
α
F
FA
FB
四、练习
谢谢
第三章
相互作用——力
3.4 力的合成和分解
目录
一、上节回溯
三、小结
四、练习
二、知识讲解
1.作用力和反作用力
2.牛顿第三定律
3.受力分析
一、上节回溯
现实生活中,一个物体往往不止受到一个力的作用,一个静止的物体,在某平面上受到 5 个力的作用,你能判断它将向哪个方向运动吗?
若是有一个力的单独作用能够代替这 5 个力的作用,这个问题是不是就简单了,那么这个力与被替代的力有什么关系呢?
问题引入
二、知识讲解——合力与分力
生活中常常见到这样的事例:一个力的单独作用与两个力或者更多的力共同作用,效果相同。例如:下图中作用效果,即是保持水桶或是吊灯被提起且静止不动。很明显 F 一个力的作用与 F1和 F2 两个力的作用等效。
合力与分力
图 3.4-1 水桶所受拉力示意图
图 3.4-2 吊灯所受拉力示意图
二、知识讲解——合力与分力
定义:假设一个力单独作用的效果跟某几个力共同作用的效果相同,这个力就叫作那几个力的合力。假设几个力共同作用的效果跟某个力单独作用的效果相同,这几个力就叫作那个力的分力。
合力与分力
分力
合力
等效替代
F
F1、F2、F3…
二、知识讲解——合力与分力
1.力的合成:求几个力的合力的过程;
2.力的分解:求一个力的分力的过程。
力的合成和分解
分力
合力
等效替代
F
F1、F2、F3…
力的合成
力的分解
二、知识讲解——力的合成和分解
如果两个力在同一条直线上,如何求它们的合力?
如果两个力的方向不在同一条直线上,如何求它们的合力?
互成角度的两个力与它们的合力之间有什么关系呢?
思考
二、知识讲解——力的合成和分解
实验目的:探究合力 F 与互成角度的两个力 F1、F2 有什么关系。
设计思路:
(1)力的作用效果:使物体发生形变、改变物体运动状态。如何选择?
(2)如何保证力的作用效果相同?
(3)力的大小如何测量?
(4)力的方向如何确定?
(5)如何记录数据?
探究互成角度的力的合成规律
二、知识讲解——力的合成和分解
请阅读课本“实验”栏目下的内容回答下列问题:
1. 实验中需要用到哪些仪器?
2. 如何提供合力与分力?
如何保证合力与分力的作用效果相同?
3. 在实验过程中,需要记录哪些数据?如何记录?
4. 如何处理记录下来的信息?
5. 要使得测量尽可能地精确,需要注意哪些实验操作细节?
探究互成角度的力的合成规律
二、知识讲解——力的合成和分解
演示实验
1
0
2
3
4
5
N
1
0
2
3
4
5
N
1
0
2
3
4
5
N
记录效果
记录方向
二、知识讲解——力的合成和分解
如何保证用两个弹簧秤和一个弹簧秤拉动橡皮筋的力是等效的?
弹簧秤、细绳、橡皮条是否必须与木板平行 ?
两个分力的大小是用绳长表示吗?
如何减小本实验的偶然误差?
两个分力所用的细绳可以用橡皮绳代替吗?
F 与 F′ 谁是理论值,谁是测量值?
回顾实验
二、知识讲解——力的合成和分解
经过多次实验探究我们会发现,求两个力的合成,如果以表示这两个力的有向线段为邻边作平行四边形,这两个邻边之间的对角线就代表合力的大小和方向。这个规律就叫作平行四边形定则。
实验结论
二、知识讲解——力的合成和分解
如图,研究位移时,可以看出人直接沿 AC 的位移与从 A 到 B 再到 C 的位移相同,因此 AC 是两段位移 AB 和 BC 的合位移。因此位移的合成遵从平行四边形定则。
矢量和标量
A
C
B
(1)矢量:既有大小,也有方向,相加遵从平行四边形定则。
(2)标量:只有大小,没有方向,相加遵从算数运算法则。
二、知识讲解——力的合成和分解
讨论:两个分力大小不变,改变分力的夹角,合力的变化。
力的合成
图例 θ F
最大 θ=0° F=F1+F2
0°< θ < 90° F1+F2> F>
θ=90° F=
90°< θ < 180° |F1-F2|
F1
F2
F
F2
F1
F
θ
F2
F1
F
θ
F2
F1
F
θ
F1
F2
F
二、知识讲解——力的合成和分解
力的分解也是遵从平行四边形定则的。
思考:已知两个分力(邻边),则合力(对角线)是唯一的。那么已知合力(对角线),求分力(邻边),答案是否唯一呢?
力的分解
F
结论:如果没有其他限制,同一个力可以分解为无数组大小、方向不同的分力。
注意:不能说成按照力的作用效果进行分解,可以说成根据解决问题的需要进行分解。
二、知识讲解——力的合成和分解
1.如图所示,请判断下列说法正确吗?
(1)F1 就是物块对斜面的压力;
(2)F2 就是物块受到的摩擦力。
常见的问题
G
F2
F1
2.两个力 F1 和 F2 之间的夹角为 θ,其合力为 F 。请判断以下说法是否正确,并简述理由。
(1)合力 F 总比分力 F1 和 F2 中的任何一个力都大。
(2)若 F1 和 F2 大小不变,θ 角越小,则合力 F 就越大。
(3)若夹角 θ 不变,F1 大小不变,F2 增大,则合力 F 一定大。
二、知识讲解——力的合成和分解
常见的问题
3.同一个力,约束条件不同,分解出的两个分力大小、方向就可以不同。
G
G
F2
F1
θ
θ
θ
θ
思考:当挡板与斜面间的夹角逐渐增大的过程中,两个压力的大小怎样变化?
F2
F1
二、知识讲解——力的合成和分解
学以致用
我们在练习引体向上时,双手如何更省力?
双手越接近竖直越省力
F = G
二、知识讲解——力的合成和分解
学以致用
例题:静止在倾斜桥面的汽车,其重力为 G,桥面倾角为 α 。把重力沿平行于桥面和垂直于桥面方向分解为 G1 和 G2 ,求这两个分力的大小。
G1
G2
y
x
G
平行于斜面
使物体下滑的分力 G1
垂直于斜面
使物体紧压斜面的分力 G2
G1=G sin
G2=G cos
增大,G1 增大, G2减小
二、知识讲解——力的合成和分解
学以致用
为什么桥梁要修很长的引桥?
减小倾角,使汽车重力沿桥面的分力减小,利于车辆平缓的上下桥面。
二、知识讲解——力的合成和分解
学以致用
劈的剖面是一个等腰三角形,使用劈的时候,在劈背上加力 F,这个力产生两个效果,使劈的两个侧面推压物体,把物体劈开。设劈背的宽度是 d,劈的侧面的长度是 L。试求:F1 和 F2 的大小。
d
F
F1
F2
力的放大
思考:为什么厚度小的斧头更加锋利?
L
二、知识讲解——力的合成和分解
学以致用
资料
斜拉桥的钢索有什么作用?
F4
F2
F
F '
F3
F1
θ
θ
“拽起” 桥面。海河上的保定桥在河内不设桥墩,而是靠斜拉索的拉力“拽起” 桥面。
二、知识讲解——力的合成和分解
学以致用
资料
斜拉桥的桥塔为什么建很高?
F4
F2
F
F '
F3
F1
θ
θ
桥重一定时,桥塔越高,钢索与水平面的夹角越大,钢索上的拉力越小。
二、知识讲解——力的合成和分解
1.合力
2.分力
3.力的合成
4.力的分解
5.平行四边形定则
6.矢量和标量
三、小结
四、练习
1.有两个力,一个是10 N,一个是 2 N,它们的合力可能等于 5 N,10 N,15 N 吗?合力最大值为多少?最小值为多少?
答:两个力的方向同时,即夹角为 0° 合力最大,最大值为 12 N 。两个力的方向相反时,即夹角为 180 ° 合力最小,最小值为 8 N 。在两个力的夹角从0°逐渐增大到180° 时,合力逐渐减小,即合力大小在 8 N 到 12 N 之间 。所以可能为 10 N 不可能为 5 N 或 15 N 。
答:当两个力的合力为零时,一个力向东,大小为 6 N ,则另一个力必定向西,且大小也为 6 N 。向东的力改为向南时,两个力互相垂直,大小相等,所以用有向线段表示这两个力,构成的平行四边形为正四边形。所以合力的大小为6 N ,方向为西偏南 45 ° 的方向。
2.有两个力,它们的合力为 0 。现把其中一个向东的 6 N 的力改为向南(大小不变),它们合力的大小、方向如何?
四、练习
答:可以将 F 按如图所示的方式分解。
由图可知,FA= ,FB= 。
代入数据可得:尖劈对 A 侧的压力为 FA=20 N ,
对B侧的压力为FB= 10 N
3.(2021山东青岛高一上期中)如图所示吗,表面光滑、重力不计的尖劈,插在缝 A、B 之间,尖劈的一个角为 α=30°,在尖劈背上加一压力 F=10 N,则尖劈对 A 的侧压力和对 B 的侧压力分别为多大?
F
A
B
α
α
F
FA
FB
四、练习
谢谢
