13.4课题学习 最短路径问题—八年级数学人教版上册课时优化训练(含详解)
文档属性
| 名称 | 13.4课题学习 最短路径问题—八年级数学人教版上册课时优化训练(含详解) | 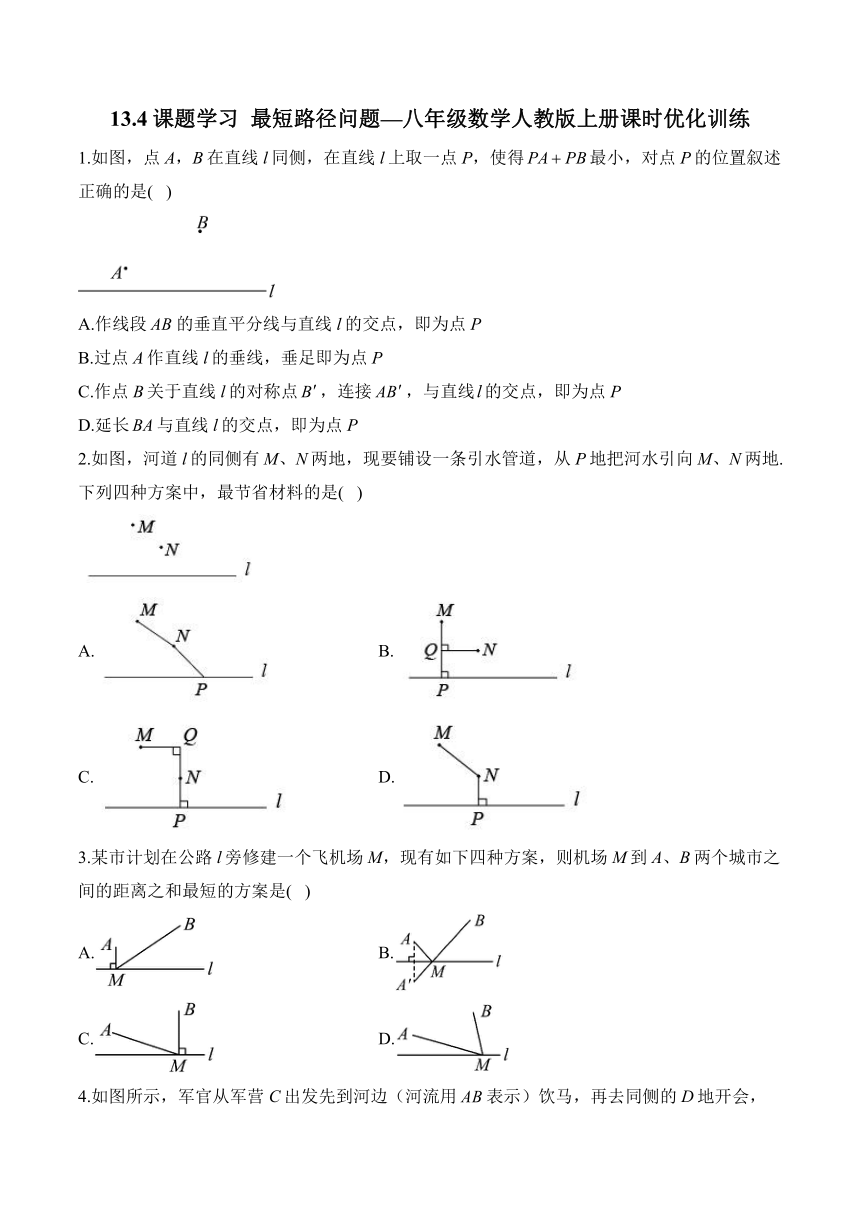 | |
| 格式 | docx | ||
| 文件大小 | 493.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-10 11:11:10 | ||
图片预览



文档简介
13.4课题学习 最短路径问题—八年级数学人教版上册课时优化训练
1.如图,点A,B在直线l同侧,在直线l上取一点P,使得最小,对点P的位置叙述正确的是( )
A.作线段的垂直平分线与直线l的交点,即为点P
B.过点A作直线l的垂线,垂足即为点P
C.作点B关于直线l的对称点,连接,与直线的交点,即为点P
D.延长与直线l的交点,即为点P
2.如图,河道l的同侧有M、N两地,现要铺设一条引水管道,从P地把河水引向M、N两地.下列四种方案中,最节省材料的是( )
A. B.
C. D.
3.某市计划在公路l旁修建一个飞机场M,现有如下四种方案,则机场M到A、B两个城市之间的距离之和最短的方案是( )
A. B.
C. D.
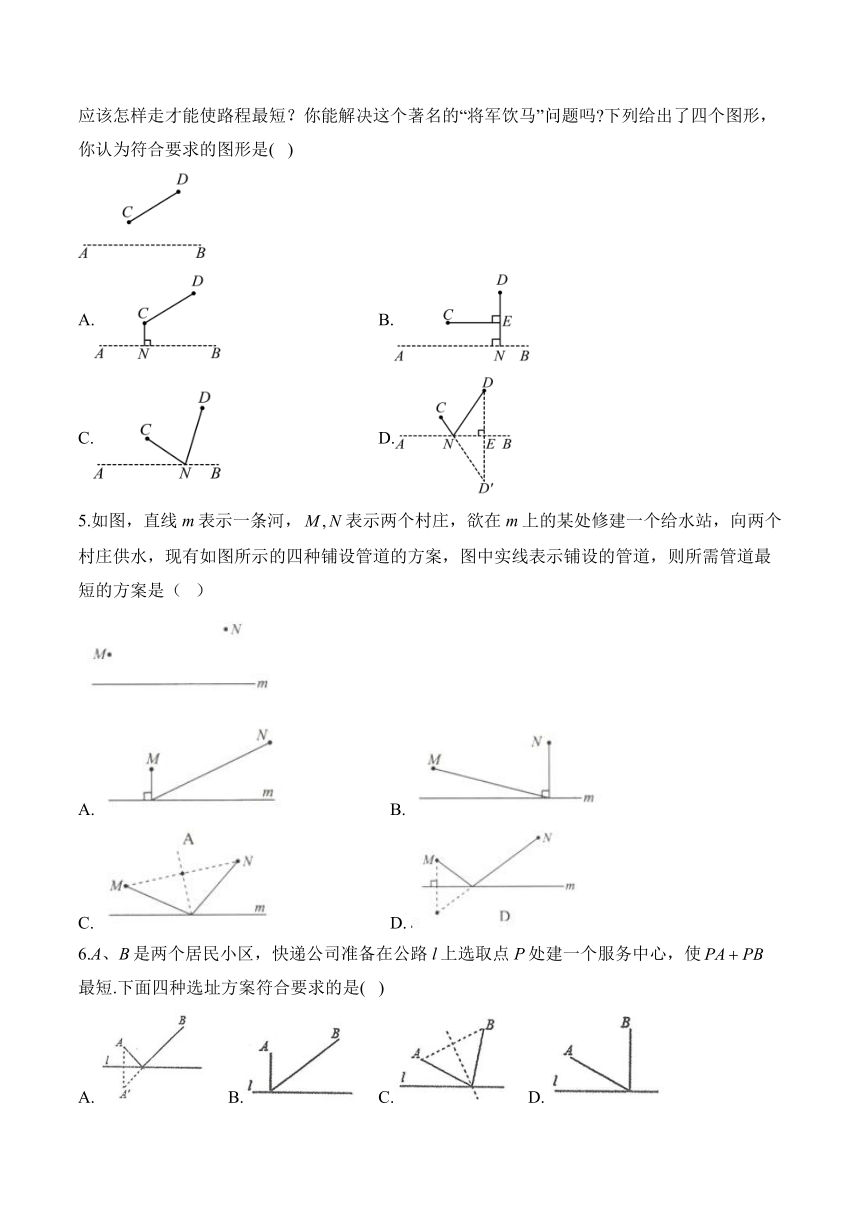
4.如图所示,军官从军营C出发先到河边(河流用表示)饮马,再去同侧的D地开会,应该怎样走才能使路程最短?你能解决这个著名的“将军饮马”问题吗 下列给出了四个图形,你认为符合要求的图形是( )
A. B.
C. D.
5.如图,直线m表示一条河,表示两个村庄,欲在m上的某处修建一个给水站,向两个村庄供水,现有如图所示的四种铺设管道的方案,图中实线表示铺设的管道,则所需管道最短的方案是( )
A. B.
C. D.
6.A、B是两个居民小区,快递公司准备在公路l上选取点P处建一个服务中心,使最短.下面四种选址方案符合要求的是( )
A. B. C. D.
7.小王准备在红旗街道旁建一个送奶站,向居民区A,B提供牛奶,要使A,B两小区到送奶站的距离之和最小,则送奶站C的位置应该在( ).
A. B.
C. D.
8.有一条以互相平行的直线为岸的河流,其两侧有村庄A和村庄B,现在要在河上建一座桥梁(桥与河岸垂直),使两村庄之间的距离最短,从作图痕迹上来看,你认为正确的是( )
A.
B.
C.
D.
9.如图,牧童在A处放牛,其家在B处,到河岸的距离分别为和,且,若点A到河岸的中点的距离为500m,则牧童从A处把牛牵到河边饮水再回家,最短距离是 m
10.如图,点P,点Q分别代表两个村庄,直线l代表两个村庄中间的一条公路.根据居民出行的需要,计划在公路l上的某处设置一个公交站.
(1)若考虑到村庄P居住的老年人较多,计划建一个离村庄P最近的车站,请在公路l上画出车站的位置(用点M表示),依据是___________________;
(2)若考虑到修路的费用问题,希望车站的位置到村庄P和村庄Q的距离之和最小,请在公路l上画出车站的位置(用点N表示),依据是___________________.
11.如图,点A、B在直线l同侧,请你在直线l上画出一点P,使得的值最小,画出图形并保留作图痕迹.
12.如图,山娃星期天从A处赶了几只羊到草地吃草,然后赶羊到小河饮水,之后再回到B处的家,假设山娃赶羊走的都是直路,请你为他设计一条最短的路线,标明吃草与饮水的位置.
答案以及解析
1.答案:C
解析:正确作法如下:如图,作点B关于直线l的对称点,连接,与直线l的交点,即为点P,
,
理由如下:在l上异于点P的位置任取一点H,连接,,,
,
B、关于直线l对称,
,
,
最短,
故选:C.
2.答案:D
解析:依据垂线段最短,以及两点之间,线段最短,可得最节省材料的是:
故选:D.
3.答案:B
解析:作点A关于直线l的对称点,连接交直线l于M,
根据两点之间线段最短,可知机场M到A、B两个城市之间的距离之和最短.
故选:B.
4.答案:D
解析:由选项D中图可知:
作D点关于直线的对称点,连接交于点N,
由对称性可知,,
,
当C、N、三点共线时,的距离最短,
故选:D.
5.答案:D
解析:作点M关于直线m的对称点,连接交直线m于P.根据两点之间,线段最短,可知选项D铺设的管道最短.
6.答案:A
解析:如图:
在l上任找一点连接,,,
直线l垂直平分,
,
,
在中,两边之和大于第三边,
,
即:,
A方案中最短,
故答案选A.
7.答案:C
解析:如图:作点A关于街道的对称点,连接交街道所在直线于点C,
,
,
在街道上任取除点C以外的一点,连接,,,
,
在中,两边之和大于第三边,
,
,
点C到两小区送奶站距离之和最小.
故选:C.
8.答案:C
解析:根据题意,应先把点A(或点B)沿着它们垂直于河岸的方向平移,使平移的距离等于河宽,再作两点间的线段故选C.
9.答案:1000
解析:如图,作点A关于的对称点,连接与相交于点M,则牧童从A处把牛牵到河边饮水再回家,最短距离是的长。
,.
又,
.
点A到河岸的中点的距离为500m,
到M的距离为500m,
故最短距离是1000m
10.答案:(1)画图见解析;直线外一点与直线上各点连接的所有线段中垂线段最短
(2)画图见解析;两点之间线段最短
解析:(1)如图,点M即为所示.依据是直线外一点与直线上各点连接的所有线段中垂线段最短
(2)如图,点N即为所示.依据是两点之间线段最短;
故答案为直线外一点与直线上各点连接的所有线段中垂线段最短;两点之间线段最短.
11.答案:见详解
解析:如图所示,
作法:1.作点B关于直线l的对称点,
2.连接,交直线l于点P,连接,
则点P即为所求
证明:作点B关于直线l的对称点,连接,交直线l于点P,连接
直线l垂直平分,
,
,
如图:在直线l上取异于点P的另一点,连接,,,
直线l垂直平分,
,
在中,,
,
,
故的值最小,
故点P即为所求.
12.答案:见解析
解析:如图,作点A关于的对称点E,点B关于的对称点F,连接,分别交,于点C,D.
点C为吃草的位置,点D为饮水的位置,则是他走的最短路线.
1.如图,点A,B在直线l同侧,在直线l上取一点P,使得最小,对点P的位置叙述正确的是( )
A.作线段的垂直平分线与直线l的交点,即为点P
B.过点A作直线l的垂线,垂足即为点P
C.作点B关于直线l的对称点,连接,与直线的交点,即为点P
D.延长与直线l的交点,即为点P
2.如图,河道l的同侧有M、N两地,现要铺设一条引水管道,从P地把河水引向M、N两地.下列四种方案中,最节省材料的是( )
A. B.
C. D.
3.某市计划在公路l旁修建一个飞机场M,现有如下四种方案,则机场M到A、B两个城市之间的距离之和最短的方案是( )
A. B.
C. D.
4.如图所示,军官从军营C出发先到河边(河流用表示)饮马,再去同侧的D地开会,应该怎样走才能使路程最短?你能解决这个著名的“将军饮马”问题吗 下列给出了四个图形,你认为符合要求的图形是( )
A. B.
C. D.
5.如图,直线m表示一条河,表示两个村庄,欲在m上的某处修建一个给水站,向两个村庄供水,现有如图所示的四种铺设管道的方案,图中实线表示铺设的管道,则所需管道最短的方案是( )
A. B.
C. D.
6.A、B是两个居民小区,快递公司准备在公路l上选取点P处建一个服务中心,使最短.下面四种选址方案符合要求的是( )
A. B. C. D.
7.小王准备在红旗街道旁建一个送奶站,向居民区A,B提供牛奶,要使A,B两小区到送奶站的距离之和最小,则送奶站C的位置应该在( ).
A. B.
C. D.
8.有一条以互相平行的直线为岸的河流,其两侧有村庄A和村庄B,现在要在河上建一座桥梁(桥与河岸垂直),使两村庄之间的距离最短,从作图痕迹上来看,你认为正确的是( )
A.
B.
C.
D.
9.如图,牧童在A处放牛,其家在B处,到河岸的距离分别为和,且,若点A到河岸的中点的距离为500m,则牧童从A处把牛牵到河边饮水再回家,最短距离是 m
10.如图,点P,点Q分别代表两个村庄,直线l代表两个村庄中间的一条公路.根据居民出行的需要,计划在公路l上的某处设置一个公交站.
(1)若考虑到村庄P居住的老年人较多,计划建一个离村庄P最近的车站,请在公路l上画出车站的位置(用点M表示),依据是___________________;
(2)若考虑到修路的费用问题,希望车站的位置到村庄P和村庄Q的距离之和最小,请在公路l上画出车站的位置(用点N表示),依据是___________________.
11.如图,点A、B在直线l同侧,请你在直线l上画出一点P,使得的值最小,画出图形并保留作图痕迹.
12.如图,山娃星期天从A处赶了几只羊到草地吃草,然后赶羊到小河饮水,之后再回到B处的家,假设山娃赶羊走的都是直路,请你为他设计一条最短的路线,标明吃草与饮水的位置.
答案以及解析
1.答案:C
解析:正确作法如下:如图,作点B关于直线l的对称点,连接,与直线l的交点,即为点P,
,
理由如下:在l上异于点P的位置任取一点H,连接,,,
,
B、关于直线l对称,
,
,
最短,
故选:C.
2.答案:D
解析:依据垂线段最短,以及两点之间,线段最短,可得最节省材料的是:
故选:D.
3.答案:B
解析:作点A关于直线l的对称点,连接交直线l于M,
根据两点之间线段最短,可知机场M到A、B两个城市之间的距离之和最短.
故选:B.
4.答案:D
解析:由选项D中图可知:
作D点关于直线的对称点,连接交于点N,
由对称性可知,,
,
当C、N、三点共线时,的距离最短,
故选:D.
5.答案:D
解析:作点M关于直线m的对称点,连接交直线m于P.根据两点之间,线段最短,可知选项D铺设的管道最短.
6.答案:A
解析:如图:
在l上任找一点连接,,,
直线l垂直平分,
,
,
在中,两边之和大于第三边,
,
即:,
A方案中最短,
故答案选A.
7.答案:C
解析:如图:作点A关于街道的对称点,连接交街道所在直线于点C,
,
,
在街道上任取除点C以外的一点,连接,,,
,
在中,两边之和大于第三边,
,
,
点C到两小区送奶站距离之和最小.
故选:C.
8.答案:C
解析:根据题意,应先把点A(或点B)沿着它们垂直于河岸的方向平移,使平移的距离等于河宽,再作两点间的线段故选C.
9.答案:1000
解析:如图,作点A关于的对称点,连接与相交于点M,则牧童从A处把牛牵到河边饮水再回家,最短距离是的长。
,.
又,
.
点A到河岸的中点的距离为500m,
到M的距离为500m,
故最短距离是1000m
10.答案:(1)画图见解析;直线外一点与直线上各点连接的所有线段中垂线段最短
(2)画图见解析;两点之间线段最短
解析:(1)如图,点M即为所示.依据是直线外一点与直线上各点连接的所有线段中垂线段最短
(2)如图,点N即为所示.依据是两点之间线段最短;
故答案为直线外一点与直线上各点连接的所有线段中垂线段最短;两点之间线段最短.
11.答案:见详解
解析:如图所示,
作法:1.作点B关于直线l的对称点,
2.连接,交直线l于点P,连接,
则点P即为所求
证明:作点B关于直线l的对称点,连接,交直线l于点P,连接
直线l垂直平分,
,
,
如图:在直线l上取异于点P的另一点,连接,,,
直线l垂直平分,
,
在中,,
,
,
故的值最小,
故点P即为所求.
12.答案:见解析
解析:如图,作点A关于的对称点E,点B关于的对称点F,连接,分别交,于点C,D.
点C为吃草的位置,点D为饮水的位置,则是他走的最短路线.
