人教版九年级上册数学第二十二章二次函数应用题专题训练(含解析)
文档属性
| 名称 | 人教版九年级上册数学第二十二章二次函数应用题专题训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-11 06:55:42 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
人教版九年级上册数学第二十二章二次函数应用题专题训练
1.每年5月的第二个星期日即为母亲节,“父母恩深重,恩怜无歇时”,许多市民喜欢在母亲节为母亲送鲜花,感恩母亲,祝福母亲. 节日前夕,某花店采购了一批鲜花礼盒,成本价为30元每件,分析上一年母亲节的鲜花礼盒销售情况发现,当售价为40元/件时,每天的销售量为300件,销售单价每增加10元,日均销售量减少50件.设销售单价为每件元,日均销售量为件.
(1)求出与的函数关系式;
(2)物价局要求,销售该鲜花礼盒获得的利润不得高于:
①当销售单价取何值时,该花店销售鲜花礼盒每天获得的利润为5000元 (利润销售总价成本价);
②试确定销售单价取何值时,花店销售该鲜花礼盒每天获得的利润(元)最大 并求出花店销售该鲜花礼盒每天获得的最大利润.
2.成都是一座休闲又充满幸福感的城市,眼下露营正成为成都人民一种新的周末休闲娱乐方式,经营户外用品店的小明决定设计一个等腰梯形的露营地(如图),露营地上底长120米,下底长180米,上下底相距80米,在两腰中点连接(虚线)处有一条横向通道,上下底之间有两条纵向通道,各通道的宽度相等,设通道的宽为米.(提示:两腰中点连接(虚线)是此等腰梯形中位线,其长是上下底之和的一半.)
(1)用含的式子表示横向通道的面积;
(2)当三条通道的面积是梯形露营地面积的八分之一时,求通道的宽;
(3)根据设计的要求,通道的宽不能超过8米,如果修建通道的总费用万元,花坛其绿化费用为每平方米万元,那么当通道的宽度为多少米时,所建花坛的总费用最少?最少费用是多少万元?
3.一大型商场经营某种品牌商品,该商品的进价为每件5元,根据市场调查发现,该商品每周的销售量y(件)与售价x(元/件)之间满足一次函数关系,表格记录的是某三周的有关数据:
x(元/件) 7 8 9
y(件) 8500 8000 7500
(1)求y与x的函数关系式(不求自变量的取值范围);
(2)在销售过程中要求销售单价不低于成本价,若某一周该商品的销售量不少于6000件,求这一周该商场销售这种商品获得的最大利润和售价分别为多少元?
(3)抗疫期间,该商场这种商品售价在不超过17元/件时,每销售一件商品便向某慈善机构捐赠m元(),捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.请直接写出m的取值范围.
4.如图,某校劳动实践基地用总长为80m的栅栏,围成一块一边靠墙的矩形实验田,墙长为42m.栅栏在安装过程中不重叠、无损耗,设矩形实验田与墙垂直的一边长为x(单位:m),与墙平行的一边长为y(单位:m),面积为S(单位:).
(1)直接写出y与x,S与x之间的函数解析式(不要求写x的取值范围);
(2)矩形实验田的面积S能达到吗?如果能,求x的值;如果不能,请说明理由.
(3)当x的值是多少时,矩形实验田的面积S最大?最大面积是多少?
5.抗击疫情期间,某商店购进了一种消毒用品,进价为每件8元,销售过程中发现,该商品每天的销售量y(件)与每件售价x(元)之间存在一次函数关系(其中,且x为整数),部分对应值如下表:
每件售价(元) 9 11 13
每天的销售量(件) 105 95 85
(1)求y与x的函数关系式.
(2)若该商店销售这种消毒用品每天获得425元的利润,则每件消毒用品的售价为多少元.
(3)设该商店销售这种消毒用品每天获利w(元),问:当每件消毒用品的售价为多少元时,每天的销售利润最大?最大利润是多少元?
6.某水果店包装一种果篮需要A,B两种水果,A种水果的单价比B种水果单价少2元,若用600元购进A种水果和用800元购进B种水果数量一样多,包装一盒果篮需要A种水果4斤和B种水果2斤,每盒还需包装费8元.市场调查发现:设每盒果篮的售价是x元(x是整数),该果篮每月的销量y(盒)与售价x(元)的关系式为:.
(1)求一盒果篮的成本(成本进价包装费);
(2)若每月的利润是w元,求w关于x的函数解析式(不需要写出自变量的取值范围);
(3)若每盒果篮的售价不超过m元(m是大于70的常数,且是整数),直接写出每月的最大利润.
7.某商店销售一种商品,小明经市场调查发现:该商品的周销售量(件)是售价(元件)的一次函数,其售价、周销售量、周销售利润(元)的三组对应值如表:
售价(元件)
周销售量(件)
周销售利润(元)
注:周销售利润周销售量(售价进价)
(1)求关于的函数解析式;(不要求写出自变量的取值范围)
(2)表格中,当时, ______ ,当时, ______ ;
(3)求当售价是多少时,周销售利润最大,最大利润是多少元.
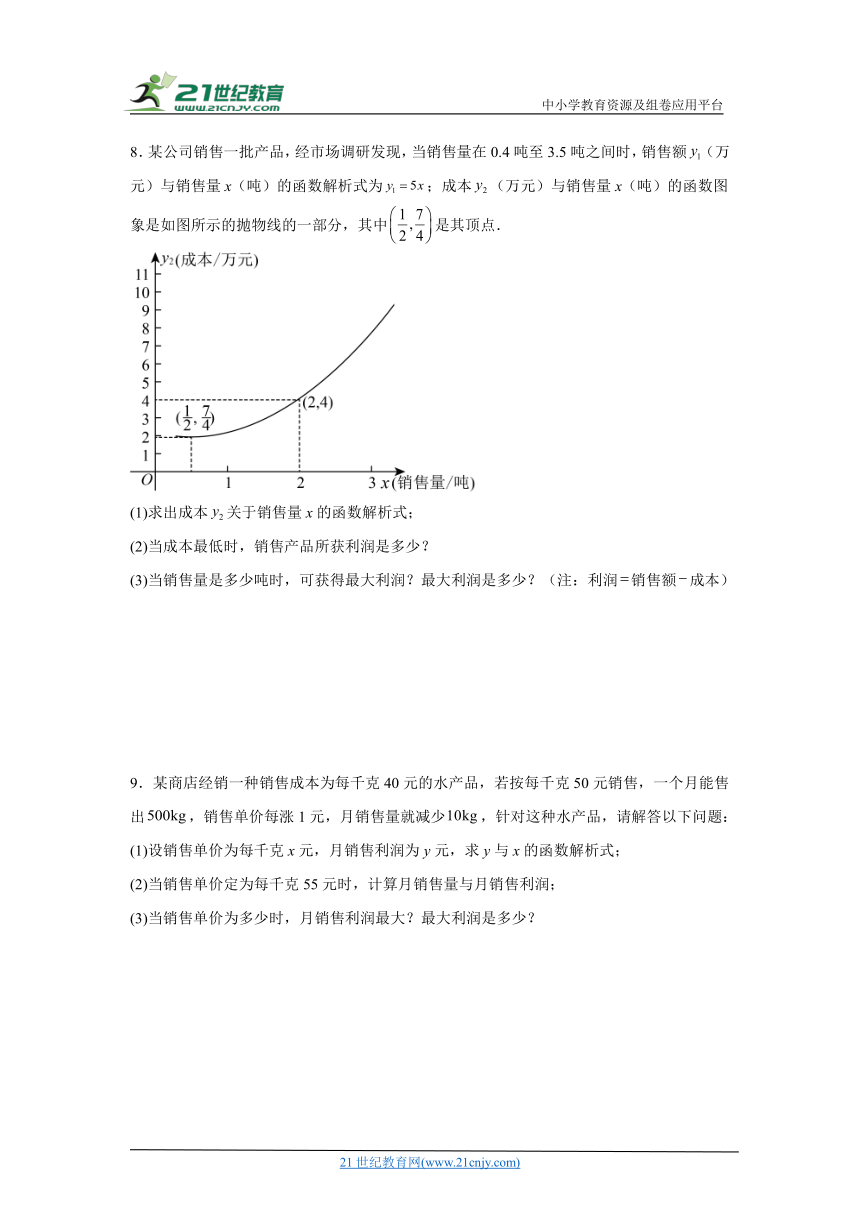
8.某公司销售一批产品,经市场调研发现,当销售量在0.4吨至3.5吨之间时,销售额(万元)与销售量x(吨)的函数解析式为;成本(万元)与销售量x(吨)的函数图象是如图所示的抛物线的一部分,其中是其顶点.
(1)求出成本关于销售量x的函数解析式;
(2)当成本最低时,销售产品所获利润是多少?
(3)当销售量是多少吨时,可获得最大利润?最大利润是多少?(注:利润销售额成本)
9.某商店经销一种销售成本为每千克40元的水产品,若按每千克50元销售,一个月能售出,销售单价每涨1元,月销售量就减少,针对这种水产品,请解答以下问题:
(1)设销售单价为每千克x元,月销售利润为y元,求y与x的函数解析式;
(2)当销售单价定为每千克55元时,计算月销售量与月销售利润;
(3)当销售单价为多少时,月销售利润最大?最大利润是多少?
10.经市场调研发现:某品牌童装平均每周可售出60件,每件盈利80元.在每件降价幅度不超过26元的情况下,若每件童装降价5元,则每周可多售出10件.
(1)降价15元后,每件童装盈利是______元,每周销售量是______件;
(2)要想每周销售这种童装盈利6000元,那么每件童装应降价多少元?
(3)若每周该品牌童装盈利为y元,不考虑其他因素,单纯从经济角度看,单价降低多少元时,每周盈利最多?最多盈利多少元?
11.如图,是篮球队员的一次投球,在图中的平面直角坐标系中,篮球运动的路线(抛物线)解析式为.
(1)求篮球运行过程中的最大高度;
(2)如果没有篮板、篮桩的阻挡,求篮球落地时所运行的水平距离;
(3)若篮圈的中心高度是3m,到投球点的水平距离是7m,则这次投球是否能命中?
12.某企业设计了一款工艺品,每件的成本是50元,为了合理定价,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)当销售单价为70元时,每天的销售利润是多少?
(2)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(3)如果该企业每天的总成本不超过7000元,那么销售单价为多少元时,每天的销售利润最大?最大利润是多少?(每天的总成本每件的成本每天的销售量)
13.为了拉动内需,让惠于农民,丰富农民的业余生活,鼓励送电脑下乡,国家决定实行政府补贴.规定每购买一台电脑,政府补贴若干元,经调查某商场销售电脑台数y(台)与补贴款额x(元)之间大致满足如图所示的一次函数关系,随着补贴款额x的不断增大,销售量也不断增加,但每台电脑的收益p(元)会相应降低且满足:.
(1)在政府补贴政策实施后,求出该商场销售电脑台数y与政府补贴款额x之间的函数关系式;
(2)在政府未出台补贴措施之前,该商场销售电脑的总收益额为多少元?
(3)要使该商场销售电脑的总收益最大,政府应将每台补贴款额x定为多少?并求出总收益的最大值.
14.心理学家发现,学生对概念的接受能力与提出概念所用的时间(分钟)之间满足函数,值越大,表示接受能力越强.
(1)在什么范围内,学生的接受能力逐步增强?在什么范围内,学生的接受能力逐步降低?
(2)第分钟时,学生的接受能力是多少?
(3)第几分钟时,学生的接受能力最强?
15.某影像公司经过市场调研,发现制作某种毕业相册的销量y(套)是售价x(元/套)的一次函数,其售价、销售量、销售利润w(元)的三组对应值如下表:
售价x(元/套) 130 150 180
销售量y(套) 210 150 60
销售利润w(元) 10500 10500 6000
注:销售利润销售量(售价成本价)
(1)求y关于x的函数解析式(不要求写出自变量的取值范围);
(2)求制作该毕业相册的成本价;
(3)当售价为多少元时,销售利润最大?最大利润是多少?
(4)已知影像公司在七月份为某校九年级制作这种毕业相册的过程中,尽可能让利于学生,最后所得利润为9600元,求这种毕业相册的售价.
16.实行垃圾分类,关系广大人民群众生活环境,关系节约使用资源,也是社会文明水平的一个重要体现.为改善城市生态环境,某公司为配合国家垃圾分类入户的倡议,设计了一款成本为元/个的多用途垃圾桶投放市场,经试销发现,销售量(个)与销售单价(元)符合一次函数关系:当时,;当时,.
(1)若该公司获得利润为元,试写出利润与销售单价之间的函数解析式;
(2)若物价部门限定该产品的销售单价不得超过30元/个,那么定价为多少元时才可获得最大利润?
17.小区一水果店购进一种新型蟠桃,蟠桃进价为每千克40元.水果店老板发现:销售量y(千克)与销售单价x(元/千克)之间的关系可近似地看作一次函数,且当时,;当时,,且.
(1)求y关于x的函数解析式:
(2)如果想要每月获得2400元的利润,那么销售单价应定为每千克多少元.
(3)当蟠桃售价每千克多少元时,利润最大,最大利润是多少元.
18.某公司销售一批产品,经市场调研发现,当销售量在0.4吨至3.5吨之间时,销售额(万元)与销售量x(吨)的函数解析式为;成本(万元)与销售量x(吨)的函数图象是如图所示的抛物线的一部分,其中是其顶点.
(1)求出成本关于销售量x的函数解析式;
(2)当成本最低时,销售产品所获利润是多少?
(3)当销售量是多少吨时,可获得最大利润?最大利润是多少?(注:利润=销售额成本)
19.《劳动教育》成为一门独立的课程,某校率先行动,在校园内开辟了一块劳动教育基地.八年级数学兴趣小组在课余时间里,利用一面学校的墙(墙的最大可用长度为22米),现用长为34米的篱笆(篱笆正好要全部用完,且不考虑接头的部分),围成中间隔有一道篱笆的长方形菜地,在菜地的前端各设计了两个宽1米的小门,供同学们进行劳动实践.设垂直于墙的篱笆边长为米.
(1)求当为何值时,围成的菜地面积为81平方米;
(2)要想围成菜地面积为120平方米,可能吗?请计算说明理由;
(3)围成菜地的最大面积为 平方米.
20.“端午节”吃粽子是中国传统习俗,在端午节来临前,某超市购进一种品牌粽子,每盒进价是40元,并规定每盒售价不得少于50元,日销售量不低于350盒,根据以往销售经验发现,当每盒定价为50元时,日销售量为500盒,每盒售价每提高1元,日销售量减少10盒,设每盒售价为x元,日销售量为P盒.
(1)当时,P等于______;
(2)当每盒售价定为多少元时,日销售利润W(元)最大?最大利润是多少?
(3)小强说:“当日销售利润最大时,日销售额不是最大.”小红说:“当日销售利润不低于8000元时,每盒售价x的范围为.”你认为他们的说法正确吗?
21.某超市购入一批进价为10元/盒的糖果进行销售,经市场调查发现:销售单价不低于进价时,日销售量y(盒)与销售单价x(元)是一次函数关系,下表是y与x的几组对应值.
销售单价x/元 … 12 14 16 18 20 …
销售量y/盒 … 56 52 48 44 40 …
(1)求y与x的函数表达式;
(2)糖果销售单价定为多少元时,所获日销售利润最大,最大利润是多少?
(3)若超市决定每销售一盒糖果向儿童福利院赠送一件价值为m元的礼品,赠送礼品后,为确保该种糖果日销售获得的最大利润为392元,求m的值.
22.某广场建了一座圆形音乐喷水池,在池中心竖直安装一根水管,安装在水管顶端A处的圆形喷头向四周喷水,且各个方向喷出的抛物线形水柱形状相同.如图1,以池中心O点为坐标原点,水平方向为x轴,所在的直线为y轴,建立平面直角坐标系.x轴上的点C,D为水柱的落水点,若落地直径,使喷出的抛物线形水柱在与池中心的水平距离为处达到最高.
(1)求图1中右边抛物线的解析式;
(2)计划在图1中的线段上的点B处竖立一座雕像,雕像高,若想雕像不碰到水柱,请求出线段的取值范围;
(3)圆形水池的直径为,喷水造型会随着音乐节奏起伏而变化,从而产生一组不同的抛物线(如图2),若右侧抛物线顶点始终在直线上,当喷出的抛物线水柱最大高度为时,水柱会喷到圆形水池之外吗?请说明理由.
23.某次军训中,借助小山坡的有利地势,优秀学员小华在教官的指导下用手榴弹(模拟手榴弹)进行一次试投:如图所示,把小华投出的手榴弹的运路线看成一条开口向下的抛物线,抛物线过原点,手榴弹飞行的最大高度为10米,此时它的水平飞行距离为20米,山坡的坡度为,坡顶A处的水平距离为30米.
(1)求这条抛物线的函数解析式(不要求写出自变量的取值范围);
(2)小华投出的手榴弹能否越过坡顶A?请说明理由;
(3)若,坡上趴着几位“敌军”同学,手榴弹落地后会爆炸,爆炸后距落地点米范围内会受波及,问手榴弹落地爆炸后是否会波及斜坡?请说明理由.
24.某工厂生产某种玩具的成本价为36元件,工厂决定采取电商销售和门店销售两种方式销售该玩具.前20天电商销售:售价为62元件;后20天门店销售:第20天售价为62元件,此后售价每天比前一天每件降低0.5元.已知两种销售方式第天的销售数量(件均满足且为整数).
(1)求门店销售方式每天的售价y(元/件)与x的函数关系式;
(2)该玩具销售过程中,在第几天获得的利润W(元)最大?最大利润是多少?
(3)该玩具销售过程中,请直接写出日销售利润不低于3510元的天数.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.(1)
(2)①当销售单价时,该花店销售鲜花礼盒每天获得的利润为5000元;②销售单价时,花店销售该鲜花礼盒每天获得的利润最大,最大利润为6000元
【分析】本题考查二次函数的实际应用、一元二次方程的实际应用、一次函数的实际应用,理解题意,正确求得相关的函数关系式及方程是解答的关键.
(1)根据题意求解函数关系式即可;
(2)①根据利润销售总价成本价日均销售量×单件利润列方程求解即可;
②根据利润日均销售量×单件利润得到函数关系式,利用二次函数的性质求解即可.
【详解】(1)解:由题意,,
即与的函数关系式为;
(2)解:由题意,,
∴,
①根据题意,得,
整理,得,
解得,,
∵,,
∴,
答:当销售单价时,该花店销售鲜花礼盒每天获得的利润为5000元;
②由题意,,
∵,,
∴当时,y有最大值,最大值为,
答:销售单价时,花店销售该鲜花礼盒每天获得的利润最大,最大利润为6000元.
2.(1)横向甬道的面积为
(2)甬道的宽为
(3)所以当通道的宽度为8米时,所建花坛的总费用最少,最少费用是万元
【分析】本题考查了二次函数的应用,掌握梯形的面积公式及二次函数的性质是解题的关键.
(1)根据梯形的面积公式求解;
(2)根据“三条通道的面积是梯形露营地面积的八分之一”列方程求解;
(3)先根据费用等于面积乘以单价,列出函数关系式,再根据二次函数的性质求解.
【详解】(1)解:横向甬道的面积为:;
答:横向甬道的面积为;
(2)依题意:,
整理得:,
(不符合题意,舍去),
答:甬道的宽为;
(3)设建设花坛的总费用为y万元,
则:,
即:,
,
随x的增大而减小,
,
当米时,总费用最少.
即最少费用为:万元,
所以当通道的宽度为8米时,所建花坛的总费用最少,最少费用是万元.
3.(1)
(2)这一周该商场销售这种商品获得的最大利润为元,售价为12元/件
(3)
【分析】此题主要考查二次函数的实际应用,解题的关键是熟知待定系数法的应用、根据题意找到数量关系列出函数关系式.
(1)根据待定系数法即可求出一次函数的解析式;
(2)先根据题意求出x的取值,再由利润的关系列出利润为w关于x的二次函数,化为顶点式即可求解;
(3)根据题意可知,再根据对称轴的特点列出关于m的不等式,故可求解.
【详解】(1)解:设y与x的函数关系式为:,
把和代入得
,
解得,
∴;
(2)解:根据“在销售过程中要求销售单价不低于成本价,若某一周该商品的销售量不少于件,
得:
解得,,
设利润为w元,根据题意得,
,
∵,
∴当时,w随x的增大而增大,
∵,且x为正整数,
∴当时,w取最大值为:,
答:这一周该商场销售这种商品获得的最大利润为元,售价为12元;
(3)解:根据题意得,,
∴对称轴为,
∵,
∴当时,w随x的增大而增大,
∵该商场这种商品售价不大于17元/件时,捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.
∴,解得,
∵,
∴.
4.(1),
(2)
(3)当时,实验田的面积S最大,最大面积是
【分析】本题考查了矩形的性质,二次函数的实际应用,计算的取值范围是解题的关键.
(1)根据,求出与的函数解析式,根据矩形面积公式求出与的函数解析式;
(2)先求出的取值范围,再将代入函数中,求出的值;
(3)将与的函数配成顶点式,求出的最大值.
【详解】(1)解:,
,
,
;
(2),
,
,
,
当时,,
,
,
,
当时,矩形实验田的面积能达到;
(3),
当时,有最大值.
5.(1)
(2)每件消毒用品的售价为 13 元
(3)当每件消毒用品的售价为 15 元时, 最大利润是 525 元
【分析】(1)待定系数法求解即可;
(2)依题意,利润,令,则,计算求解满足要求的值即可;
(3)根据二次函数的性质以及的取值范围进行求解即可.
【详解】(1)解:设与的函数关系式为 ,
将 代入得,
解得,
,
与的函数关系式为;
(2)解:利润,
令,
则,
解得或(不合题意,舍去),
每件消毒用品的售价为 13 元;
(3)解:由(2)知,
,
当时,随着的增大而增大,
当时,,此时利润最大,
当每件消毒用品的售价为15元时, 最大利润是525元.
【点睛】本题考查了代行系数法求一次函数的解析式,一元二次方程的实际应用,二次函数的应用,二次函数的图象与性质.解题的关键在于对相关知识的熟练掌握与灵活运用.
6.(1)一盒果篮的成本为48元
(2)
(3)每月的最大利润为12960元
【分析】此题考查了分式方程的应用,二次函数的应用,二次函数的性质,正确理解题意列得方程及函数关系式是解题的关键.
(1)设A种水果的单价为a元,则B种水果的单价为元,根据用600元购进A种水果和用800元购进B种水果数量一样多列分式方程解答;
(2)根据利润=每盒果篮的利润×销量得到函数解析式;
(3)当且m为整数时,根据函数的性质求解即可.
【详解】(1)解:设A种水果的单价为a元,则B种水果的单价为元.
依题意,得,
解得:,
经检验,是原分式方程的解,,
∴一盒果篮的成本为:(元);
(2)解:依题意,得;
(3)解:由(2)可知每月的利润,
可化简为,
当且m为整数时,
∵,
∴当时w最大,此时:,
∴每月的最大利润为12960元.
7.(1)
(2),
(3)当售价是元件时,周销售利润最大,最大利润是元
【分析】本题考查了待定系数法求一次函数的解析式及二次函数在实际问题中的应用,理清题中的数量关系并明确二次函数的性质是解题的关键.
(1)设关于的函数解析式为,用待定系数法求解即可;
(2)该商品进价等于周销售利润除以周销售量,再减去进价;
(3)根据周销售利润周销售量售价进价,列出关于的二次函数,根据二次函数的性质可得答案.
【详解】(1)解:设关于的函数解析式为,将,分别代入得:
,
解得.
关于的函数解析式为.
(2)解:∵该商品进价是元件;
当时,,当时,元,
故答案为:,;
(3)解:由题意得:
二次项系数,抛物线开口向下,
当售价是元件时,周销售利润最大,最大利润是元.
8.(1)
(2)销售产品所获利润是0.75万元
(3)当销售量3吨时,获得最大利润,最大利润为10.5万元
【分析】本题考查的是二次函数的实际应用:
(1)根据题意可设抛物线为:,再把代入,即可求解;
(2)根据二次函数的性质可得当时,成本最小值为,此时,即可求解;
(3)设销售利润为W万元,根据题意可得W关于x的函数关系式,再根据二次函数的性质,即可求解.
【详解】(1)解:根据题意可设抛物线为:,
把代入可得:,
解得:,
∴抛物线的解析式为;
(2)解:∵,
∴当时,成本最小值为,
此时,
∴销售产品所获利润是(万元);
(3)解:设销售利润为W万元,根据题意得:
∴,
∵,
∴当时,W的值最大,最大值为10.5,
即当销售量3吨时,获得最大利润,最大利润为10.5万元.
9.(1)
(2)月销售量为,月销售利润为6750元
(3)销售单价为70元时,获得的利润最大,最大利润是9000元
【分析】本题主要考查了二次函数的应用,能正确表示出月销售量是解题的关键.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法.
(1)利润销售量单位利润,单位利润为,销售量为,据此表示利润得关系式;
(2)结合(1)计算即可;
(3)根据(1)中函数关系式,配方,利用二次函数的性质可得到总利润的最大值.
【详解】(1)解:根据题意得:,
∴y与x的函数解析式为;
(2)解:当时,销售量:,
销售利润:,
答:销售量为,销售利润为6750元;
(3)解:,
∵,
∴当时,利润最大为9000元.
答:销售单价为70元时,获得的利润最大,最大利润是9000元.
10.(1)65;90
(2)每件童装降价20元
(3)当每件童装降价25元时,每周盈利最多,最多盈利6050元
【分析】本题考查了一元二次方程及二次函数的应用,掌握平均每天售出的件数×每件盈利=每天销售的利润的运用是解题的关键,读懂题题意,找出之间的数量关系列出方程(或函数解析式)即可.
(1)根据降价后的利润=原利润-降的钱;根据每件童装降价5元,则每周可多售出10件,即可表示出每天的销售数量;
(2)设每件童装应降价x元,根据题目中的等量关系列出方程解方程即可;
(3)设每周销售这种童装利润为y,列出y与x的函数关系式,利用二次函数的性质解决问题即可.
【详解】(1)降价15元后,每件童装盈利是:元;
每周销售量是∶件.
故答案为:65;90;
(2)设每件童装应降价x元,根据题意得:
,
解得,(不合题意,舍去),
答:每件童装降价20元;
(3)设设每件童装应降价x元,每周销售这种童装利润为y元,根据题意得:
,
当时,函数有最大值6050.
答:当每件童装降价25元时,每周盈利最多,最多盈利6050元.
11.(1)篮球运行过程中的最大高度是;
(2)篮球落地时所运行的水平距离为;
(3)这次投球能命中
【分析】本题主要考查二次函数的应用和一元二次方程的应用,关键是利用二次函数的性质解答.
(1)把函数解析式化为顶点式,由函数的性质求最值;
(2)令,解方程即可;
(3)把代入解析式求出的值即可判断.
【详解】(1)解:
,
,
当时,有最大值,最大值为4,
答:篮球运行过程中的最大高度是;
(2)解:令,则,
整理得:,
解得(舍去),,
答:篮球落地时所运行的水平距离为;
(3)解:当时,,
点在抛物线上,
答:这次投球能命中.
12.(1)4000元
(2)
(3)销售单价为82元时,每天的销售利润最大,最大利润为4480.
【分析】本题主要考查的是二次函数的应用,依据题意列出每天的销售利润y与定价x的函数关系式是解题的关键.
(1)根据题意先求得当单价为70元时的销售量,然后根据利润=销售量×每件的利润求解即可;
(2)依据销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件列出函数关系式即可;
(3)每天的总成本每件的成本每天的销售量列出一元一次不等式,从而可求得x的范围,然后利用二次函数的性质可求得最大值即可.
【详解】(1)解:当销售单价为70元时,每天的销售利润元;
答:每天的销售利润是4000元
(2)解:由题得.
∵销售单价不得低于成本,
∴.且销量,
∴,解得,
∴.
∴
(3)解:∵该企业每天的总成本不超过7000元
∴,解得.
由(2)可知,
∵抛物线的对称轴为且,
∴抛物线开口向下,在对称轴右侧.
∴当时,y有最大,最大值为4480,即销售单价为82元时,每天的销售利润最大,最大利润为4480元.
13.(1)
(2)元
(3)元,元
【分析】(1)依题意设,待定系数法求解即可;
(2)当时,,当时,,根据,计算求解即可;
(3)设总收益为W元,则,由,可知当时,W有最大值,计算求解即可.
【详解】(1)解:依题意设,
将,代入得,,
解得,
∴.
(2)解:当时,,
当时,,
∴;
答:在政府未出台补贴措施之前,该商场销售彩电的总收益额为元.
(3)解:设总收益为W元,则,
∵,
∴当时,W有最大值.
答:政府应将每台补贴款额定为元时,可获得最大利润元.
【点睛】本题考查了一次函数解析式,一次函数的应用,二次函数的应用,二次函数的最值等知识.熟练掌握一次函数解析式,一次函数的应用,二次函数的应用,二次函数的最值是解题的关键.
14.(1)时,学生的接受能力逐步增强;时,学生的接受能力逐步降低
(2)
(3)
【分析】本题考查了二次函数的性质,解题的关键是掌握二次函数的性质.
(1)根据题意可得该二次函数开口向下,则函数图像在对称轴的左边随的增大而增大,在对称轴的右边随的增大而减小,据此即可求解;
(2)求出时的值即可求解;
(3)根据函数的性质可得函数在顶点处有最大值.
【详解】(1)解:函数中,,对称轴为直线,
当时,随的增大而增大,当时,随的增大而减小,
即 时,学生的接受能力逐步增强;时,学生的接受能力逐步降低;
(2)当时,,
故第分钟时,学生的接受能力是;
(3)当时,值最大,是,
故第分钟时,学生的接受能力最强.
15.(1)y关于x的函数解析式为
(2)制作该毕业相册的成本价为80元/套
(3)当售价是140元时,销售利润最大,最大利润是10800元
(4)这种毕业相册的售价为120元/套
【分析】本题考查待定系数法求函数解析式,一次函数和二次函数的实际应用,一元二次方程的实际应用.
(1)设y关于x的函数解析式为,代入表中相关数据得二元一次方程组,求解即可;
(2)设制作该毕业相册的成本价为m元/套,则,代入表中相关数据,得到关于m的方程,求解即可;
(3)根据每件的利润乘以销售量等于销售利润,得关于x的二次函数,根据二次函数的性质可得答案;
(4)根据“当所得利润为9600元”即可列出一元二次方程,求解并结合题意取舍即可解答.
【详解】(1)解:由题意可设y关于x的函数解析式为,
由表格可知当时,;当时,,
∴
解得:
∴y关于x的函数解析式为;
(2)设制作该毕业相册的成本价为m元/套
由题意可知:
由表可得当时,,,
∴,
解得:
∴制作该毕业相册的成本价为80元/套;
(3)解:由题意可知:
∵
∴当时,w有最大值,最大值为10800
答:当售价是140元时,销售利润最大,最大利润是10800元.
(4)解:当所得利润为9600元,即时,
,
解得:,,
∵由于影像公司尽可能让利于学生,
∴,
∴这种毕业相册的售价为120元/套.
16.(1)
(2)当销售单价定为元时,商场可获最大利润,最大利润是元
【分析】本题考查了二次函数的应用,熟练掌握二次函数的性质是解题关键.
(1)根据利润=销售量×(销售单价-成本)得到与之间的函数关系式,
(2)利用二次函数的性质结合已知条件求解即可.
【详解】(1)解:设销售量y(个)与销售单价x(元)一次函数关系为,
当时,;当时,.
,解得
,
∴
,
(2)解:,
,抛物线开口向下,在的左侧,随的增大而增大,
时,有最大值,最大值为元.
答:当销售单价定为元时,商场可获最大利润,最大利润是元.
17.(1)
(2)销售单价应定为每千克60元或70元
(3)当蟠桃售价每千克65元时,利润最大,最大利润是2500元
【分析】本题考查一次函数解析式,一元二次方程的实际应用,二次函数的实际应用.
(1)设y关于x的函数解析式为,根据当时,;当时,,利用待定系数法求解即可;
(2)根据利润销售量(售价进价)建立方程求解即可;
(3)设利润为,根据利润销售量(售价进价)建立函数关系式,利用二次函数的性质即可解答.
【详解】(1)解:设y关于x的函数解析式为,
根据题意得:,
解得:,
y关于x的函数解析式为;
(2)解:根据题意得:,即,
解得:,
答:销售单价应定为每千克60元或70元;
(3)解:设利润为,根据题意得:
,即,
,
,
当时,有最大值,最大值为,
答:当蟠桃售价每千克65元时,利润最大,最大利润是2500元.
18.(1)
(2)销售产品所获利润是万元;
(3)当销售量吨时,获得最大利润,最大利润为:万元;
【分析】(1)设抛物线为:,再利用待定系数法求解即可;
(2)先求解当时,成本的最小值为,再计算销售额,从而可得答案;
(3)设销售利润为万元,可得,再利用二次函数的性质解题即可;
【详解】(1)解:∵成本(万元)与销售量x(吨)的函数图象是如图所示的抛物线的一部分,其中是其顶点.
∴设抛物线为:,
把代入可得:,
解得:,
∴抛物线为;
(2)解:∵,
∴当时,成本最小值为,
∴,
∴销售产品所获利润是(万元);
(3)解:设销售利润为万元,
∴
,
当时,获得最大利润,
最大利润为:(万元);
【点睛】本题考查的是二次函数的实际应用,一次函数的应用,二次函数的性质,待定系数法的含义,熟练的建立二次函数的关系式是解本题的关键.
19.(1)米
(2)不能,理由见详解
(3)108
【分析】本题考查了一元二次方程的应用和二次函数的性质.
(1)根据各边之间的关系,可知为米,根据围成的菜地面积为平方米,可得出关于的一元二次方程,解之取其符合题意的值即可;
(2)根据菜地面积若为平方米,即可得出关于的一元二次方程,利用根的判别式即可判断;
(3)利用二次函数的性质求其最大值即可.
【详解】(1)解:∵篱笆的总长为米,菜地的前端各设计了两个宽米的小门,且垂直于墙的篱笆边为米,
∴长为米.
根据题意得:,
整理得:,
解得:,,
当时,,不符合题意,舍去;
当时,,符合题意;
故当围成的菜地面积为平方米时,为米.
(2)解:不能围成面积为平方米的菜地,理由如下:
依题意得:,
整理得:,
∵,
∴该方程无实数根,
即不能围成面积为平方米的菜地.
(3),
则当时,,
故围成菜地的最大面积为108平方米.
20.(1)400;
(2)当时,取最大值,最大值为8750元;
(3)小红错误,理由见详解.
【分析】本题考查了二次函数的应用,一元一次不等式组的应用,一次函数的应用,熟练掌握知识点,正确理解题意是解题的关键.
(1)根据每盒售价每提高1元,每天要少卖出10盒,可以得到与之间的函数关系式,把代入解析式计算即可;
(2)根据每盒利润销售盒数总利润可得关于的关系式,由二次函数性质可得答案;
(3)根据题意,在正确的的范围中求出日销售额的最大值,判断小强是否正确,根据题意列出不等式,结合的范围求出不等式的解集,判断小红是否正确.
【详解】(1)解:由题意可得,
,
即每天的销售量(盒与每盒售价(元之间的函数关系式是,
当时,,
故答案为:400.
(2)解:由题意可得,
,
由题可知:每盒售价不得少于50元,日销售量不低于350盒,
,
即,解得.
当时,取得最大值,此时,
答:当每盒售价定为65元时,每天销售的利润(元最大,最大利润是8750元;
(3)解:小强:,
设日销售额为元,
,
当时,值最大,此时,
当时,值最大,此时,
小强正确.
小红:当日销售利润不低于8000元时,
即,
,解得:,
,
当日销售利润不低于8000元时,.
故小红错误,当日销售利润不低于8000元时,.
21.(1)
(2)糖果销售单价定为25元时,所获日销售利润最大,最大利润是450元
(3)2
【分析】本题考查了二次函数的应用,解题的关键是:
(1)利用待定系数法求解即可;
(2)设日销售利润为w元,根据利润=单件利润×销售量求出w关于x的函数表达式,然后利用二次函数的性质求解即可;
(3)设日销售利润为w元,根据利润=单件利润×销售量-m×销售量求出w关于x的函数表达式,然后利用二次函数的性质求解即可.
【详解】(1)解∶设y与x的函数表达式为,
把,;,代入,得,
解得,
∴y与x的函数表达式为;
(2)解:设日销售利润为w元,
根据题意,得
,
∴当时,有最大值为450,
∴糖果销售单价定为25元时,所获日销售利润最大,最大利润是450元;
(3)解:设日销售利润为w元,
根据题意,得
,
∴当时,有最大值为,
∵糖果日销售获得的最大利润为392元,
∴,
化简得
解得,
当时,,
则每盒的利润为:,舍去,
∴m的值为2.
22.(1)
(2)
(3)水柱会落在圆形水池外,理由见解析
【分析】本题考查的知识点是待定系数法求解析式、二次函数的实际应用,解题关键是理解题意求出正确的二次函数解析式.
(1)求出点和顶点坐标为,设顶点式,利用待定系数法解答即可;
(2)将代入即可求得线段的取值范围;
(3)求出点坐标,由题意设右侧喷出的最高抛物线解析式为,求出坐标解析式后可求抛物线喷出的最远距离,即可判断水柱是否会喷到圆形水池之外.
【详解】(1)解: ,
,
,
∵喷出的抛物线形水柱在与池中心的水平距离为处达到最高.
∴顶点坐标为,
设右侧抛物线的解析式为:,
把代入得到,,
解得,
∴图1中右边抛物线的解析式为;
(2)解:当时,,
解得(不合题意,舍去)
∴线段的取值范围为;
(3)解:水柱会落在圆形水池外,理由如下:
当时,,
∴点A的坐标为,
把代入
,
,
当右侧喷出的抛物线最大高度为时,
设抛物线的解析式为:,
又上述抛物线过点,则
则,
,
当时,,
,
,(舍去),
水柱会落在圆形水池之外.
23.(1)
(2)小华投出的手榴弹能越过坡顶,见解析
(3)手榴弹落地爆炸后不会波及斜坡,见解析
【分析】本题是二次函数的应用,关键是利用待定系数法求二次函数的解析式.
(1)根据顶点坐标和过原点求出抛物线的解析式;
(2)先利用坡度求出,再根据二次函数关系式求出当时,的值,再进行比较即可;
(3)令,解方程求出手榴弹落地点到原点的距离,再利用勾股定理求出,从而求出,然后用与比较即可.
【详解】(1)解:由题意得:顶点,且抛物线过原点,
所以设抛物线的解析式为:,
把代入得:,
解得,
∴抛物线的解析式为:;
(2)小华投出的手榴弹能越过坡顶,
理由:
由(1)知,
当时,,
∵山坡的坡度为米,
∴米,
∵,
∴小华投出的手榴弹能越过坡顶;
(3)手榴弹落地爆炸后不会波及斜坡,
理由:
令,则,
解得,
∴手榴弹的落地点距离原点040米,
∵米,米,
∴(米),
∴(米),
∵,
∴手榴弹落地爆炸后不会波及斜坡.
24.(1)
(2)第32天时利润最大,为4000元
(3)日销售利润不低于3510元的天数为22天
【分析】(1)门店销售方式每天的售价第20天的售价超过20天的天数;
(2)时,电商销售的利润电商销售每件玩具的利润销售量,进而根据函数的增减性和自变量的取值范围可得对应天数及此范围内的最大利润;当时,门店销售的利润门店销售每件玩具的利润销售量,整理成顶点式,可得此范围内的对应的天数及最大利润,比较后可得最大利润及对应天数;
(3)当时,令,求得的取值范围可得相应的天数;当时,令,求得的取值范围可得相应的天数,综合两种情况可得日销售利润不低于3510元的总天数.
本题考查一次函数的应用、二次函数的应用.分电商销售和门店销售两种情况探讨函数的最大值及日销售利润不低于3510元的天数是解决本题的难点.
【详解】(1)解:依题意,∵前20天电商销售:售价为62元件;后20天门店销售:第20天售价为62元件,此后售价每天比前一天每件降低0.5元
∴
.
(2)解:①当时,
.
,
随的增大而增大,
当时,最大.的最大值为:元;
②当时,
.
,
当时,有最大值4000元,
,
第32天时利润最大,为4000元.
(3)解:由(2)知,当时,
,
解得:,
共有2天;
当时,
,
,
,共20天,
综上,日销售利润不低于3510元的天数为22天.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
人教版九年级上册数学第二十二章二次函数应用题专题训练
1.每年5月的第二个星期日即为母亲节,“父母恩深重,恩怜无歇时”,许多市民喜欢在母亲节为母亲送鲜花,感恩母亲,祝福母亲. 节日前夕,某花店采购了一批鲜花礼盒,成本价为30元每件,分析上一年母亲节的鲜花礼盒销售情况发现,当售价为40元/件时,每天的销售量为300件,销售单价每增加10元,日均销售量减少50件.设销售单价为每件元,日均销售量为件.
(1)求出与的函数关系式;
(2)物价局要求,销售该鲜花礼盒获得的利润不得高于:
①当销售单价取何值时,该花店销售鲜花礼盒每天获得的利润为5000元 (利润销售总价成本价);
②试确定销售单价取何值时,花店销售该鲜花礼盒每天获得的利润(元)最大 并求出花店销售该鲜花礼盒每天获得的最大利润.
2.成都是一座休闲又充满幸福感的城市,眼下露营正成为成都人民一种新的周末休闲娱乐方式,经营户外用品店的小明决定设计一个等腰梯形的露营地(如图),露营地上底长120米,下底长180米,上下底相距80米,在两腰中点连接(虚线)处有一条横向通道,上下底之间有两条纵向通道,各通道的宽度相等,设通道的宽为米.(提示:两腰中点连接(虚线)是此等腰梯形中位线,其长是上下底之和的一半.)
(1)用含的式子表示横向通道的面积;
(2)当三条通道的面积是梯形露营地面积的八分之一时,求通道的宽;
(3)根据设计的要求,通道的宽不能超过8米,如果修建通道的总费用万元,花坛其绿化费用为每平方米万元,那么当通道的宽度为多少米时,所建花坛的总费用最少?最少费用是多少万元?
3.一大型商场经营某种品牌商品,该商品的进价为每件5元,根据市场调查发现,该商品每周的销售量y(件)与售价x(元/件)之间满足一次函数关系,表格记录的是某三周的有关数据:
x(元/件) 7 8 9
y(件) 8500 8000 7500
(1)求y与x的函数关系式(不求自变量的取值范围);
(2)在销售过程中要求销售单价不低于成本价,若某一周该商品的销售量不少于6000件,求这一周该商场销售这种商品获得的最大利润和售价分别为多少元?
(3)抗疫期间,该商场这种商品售价在不超过17元/件时,每销售一件商品便向某慈善机构捐赠m元(),捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.请直接写出m的取值范围.
4.如图,某校劳动实践基地用总长为80m的栅栏,围成一块一边靠墙的矩形实验田,墙长为42m.栅栏在安装过程中不重叠、无损耗,设矩形实验田与墙垂直的一边长为x(单位:m),与墙平行的一边长为y(单位:m),面积为S(单位:).
(1)直接写出y与x,S与x之间的函数解析式(不要求写x的取值范围);
(2)矩形实验田的面积S能达到吗?如果能,求x的值;如果不能,请说明理由.
(3)当x的值是多少时,矩形实验田的面积S最大?最大面积是多少?
5.抗击疫情期间,某商店购进了一种消毒用品,进价为每件8元,销售过程中发现,该商品每天的销售量y(件)与每件售价x(元)之间存在一次函数关系(其中,且x为整数),部分对应值如下表:
每件售价(元) 9 11 13
每天的销售量(件) 105 95 85
(1)求y与x的函数关系式.
(2)若该商店销售这种消毒用品每天获得425元的利润,则每件消毒用品的售价为多少元.
(3)设该商店销售这种消毒用品每天获利w(元),问:当每件消毒用品的售价为多少元时,每天的销售利润最大?最大利润是多少元?
6.某水果店包装一种果篮需要A,B两种水果,A种水果的单价比B种水果单价少2元,若用600元购进A种水果和用800元购进B种水果数量一样多,包装一盒果篮需要A种水果4斤和B种水果2斤,每盒还需包装费8元.市场调查发现:设每盒果篮的售价是x元(x是整数),该果篮每月的销量y(盒)与售价x(元)的关系式为:.
(1)求一盒果篮的成本(成本进价包装费);
(2)若每月的利润是w元,求w关于x的函数解析式(不需要写出自变量的取值范围);
(3)若每盒果篮的售价不超过m元(m是大于70的常数,且是整数),直接写出每月的最大利润.
7.某商店销售一种商品,小明经市场调查发现:该商品的周销售量(件)是售价(元件)的一次函数,其售价、周销售量、周销售利润(元)的三组对应值如表:
售价(元件)
周销售量(件)
周销售利润(元)
注:周销售利润周销售量(售价进价)
(1)求关于的函数解析式;(不要求写出自变量的取值范围)
(2)表格中,当时, ______ ,当时, ______ ;
(3)求当售价是多少时,周销售利润最大,最大利润是多少元.
8.某公司销售一批产品,经市场调研发现,当销售量在0.4吨至3.5吨之间时,销售额(万元)与销售量x(吨)的函数解析式为;成本(万元)与销售量x(吨)的函数图象是如图所示的抛物线的一部分,其中是其顶点.
(1)求出成本关于销售量x的函数解析式;
(2)当成本最低时,销售产品所获利润是多少?
(3)当销售量是多少吨时,可获得最大利润?最大利润是多少?(注:利润销售额成本)
9.某商店经销一种销售成本为每千克40元的水产品,若按每千克50元销售,一个月能售出,销售单价每涨1元,月销售量就减少,针对这种水产品,请解答以下问题:
(1)设销售单价为每千克x元,月销售利润为y元,求y与x的函数解析式;
(2)当销售单价定为每千克55元时,计算月销售量与月销售利润;
(3)当销售单价为多少时,月销售利润最大?最大利润是多少?
10.经市场调研发现:某品牌童装平均每周可售出60件,每件盈利80元.在每件降价幅度不超过26元的情况下,若每件童装降价5元,则每周可多售出10件.
(1)降价15元后,每件童装盈利是______元,每周销售量是______件;
(2)要想每周销售这种童装盈利6000元,那么每件童装应降价多少元?
(3)若每周该品牌童装盈利为y元,不考虑其他因素,单纯从经济角度看,单价降低多少元时,每周盈利最多?最多盈利多少元?
11.如图,是篮球队员的一次投球,在图中的平面直角坐标系中,篮球运动的路线(抛物线)解析式为.
(1)求篮球运行过程中的最大高度;
(2)如果没有篮板、篮桩的阻挡,求篮球落地时所运行的水平距离;
(3)若篮圈的中心高度是3m,到投球点的水平距离是7m,则这次投球是否能命中?
12.某企业设计了一款工艺品,每件的成本是50元,为了合理定价,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)当销售单价为70元时,每天的销售利润是多少?
(2)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(3)如果该企业每天的总成本不超过7000元,那么销售单价为多少元时,每天的销售利润最大?最大利润是多少?(每天的总成本每件的成本每天的销售量)
13.为了拉动内需,让惠于农民,丰富农民的业余生活,鼓励送电脑下乡,国家决定实行政府补贴.规定每购买一台电脑,政府补贴若干元,经调查某商场销售电脑台数y(台)与补贴款额x(元)之间大致满足如图所示的一次函数关系,随着补贴款额x的不断增大,销售量也不断增加,但每台电脑的收益p(元)会相应降低且满足:.
(1)在政府补贴政策实施后,求出该商场销售电脑台数y与政府补贴款额x之间的函数关系式;
(2)在政府未出台补贴措施之前,该商场销售电脑的总收益额为多少元?
(3)要使该商场销售电脑的总收益最大,政府应将每台补贴款额x定为多少?并求出总收益的最大值.
14.心理学家发现,学生对概念的接受能力与提出概念所用的时间(分钟)之间满足函数,值越大,表示接受能力越强.
(1)在什么范围内,学生的接受能力逐步增强?在什么范围内,学生的接受能力逐步降低?
(2)第分钟时,学生的接受能力是多少?
(3)第几分钟时,学生的接受能力最强?
15.某影像公司经过市场调研,发现制作某种毕业相册的销量y(套)是售价x(元/套)的一次函数,其售价、销售量、销售利润w(元)的三组对应值如下表:
售价x(元/套) 130 150 180
销售量y(套) 210 150 60
销售利润w(元) 10500 10500 6000
注:销售利润销售量(售价成本价)
(1)求y关于x的函数解析式(不要求写出自变量的取值范围);
(2)求制作该毕业相册的成本价;
(3)当售价为多少元时,销售利润最大?最大利润是多少?
(4)已知影像公司在七月份为某校九年级制作这种毕业相册的过程中,尽可能让利于学生,最后所得利润为9600元,求这种毕业相册的售价.
16.实行垃圾分类,关系广大人民群众生活环境,关系节约使用资源,也是社会文明水平的一个重要体现.为改善城市生态环境,某公司为配合国家垃圾分类入户的倡议,设计了一款成本为元/个的多用途垃圾桶投放市场,经试销发现,销售量(个)与销售单价(元)符合一次函数关系:当时,;当时,.
(1)若该公司获得利润为元,试写出利润与销售单价之间的函数解析式;
(2)若物价部门限定该产品的销售单价不得超过30元/个,那么定价为多少元时才可获得最大利润?
17.小区一水果店购进一种新型蟠桃,蟠桃进价为每千克40元.水果店老板发现:销售量y(千克)与销售单价x(元/千克)之间的关系可近似地看作一次函数,且当时,;当时,,且.
(1)求y关于x的函数解析式:
(2)如果想要每月获得2400元的利润,那么销售单价应定为每千克多少元.
(3)当蟠桃售价每千克多少元时,利润最大,最大利润是多少元.
18.某公司销售一批产品,经市场调研发现,当销售量在0.4吨至3.5吨之间时,销售额(万元)与销售量x(吨)的函数解析式为;成本(万元)与销售量x(吨)的函数图象是如图所示的抛物线的一部分,其中是其顶点.
(1)求出成本关于销售量x的函数解析式;
(2)当成本最低时,销售产品所获利润是多少?
(3)当销售量是多少吨时,可获得最大利润?最大利润是多少?(注:利润=销售额成本)
19.《劳动教育》成为一门独立的课程,某校率先行动,在校园内开辟了一块劳动教育基地.八年级数学兴趣小组在课余时间里,利用一面学校的墙(墙的最大可用长度为22米),现用长为34米的篱笆(篱笆正好要全部用完,且不考虑接头的部分),围成中间隔有一道篱笆的长方形菜地,在菜地的前端各设计了两个宽1米的小门,供同学们进行劳动实践.设垂直于墙的篱笆边长为米.
(1)求当为何值时,围成的菜地面积为81平方米;
(2)要想围成菜地面积为120平方米,可能吗?请计算说明理由;
(3)围成菜地的最大面积为 平方米.
20.“端午节”吃粽子是中国传统习俗,在端午节来临前,某超市购进一种品牌粽子,每盒进价是40元,并规定每盒售价不得少于50元,日销售量不低于350盒,根据以往销售经验发现,当每盒定价为50元时,日销售量为500盒,每盒售价每提高1元,日销售量减少10盒,设每盒售价为x元,日销售量为P盒.
(1)当时,P等于______;
(2)当每盒售价定为多少元时,日销售利润W(元)最大?最大利润是多少?
(3)小强说:“当日销售利润最大时,日销售额不是最大.”小红说:“当日销售利润不低于8000元时,每盒售价x的范围为.”你认为他们的说法正确吗?
21.某超市购入一批进价为10元/盒的糖果进行销售,经市场调查发现:销售单价不低于进价时,日销售量y(盒)与销售单价x(元)是一次函数关系,下表是y与x的几组对应值.
销售单价x/元 … 12 14 16 18 20 …
销售量y/盒 … 56 52 48 44 40 …
(1)求y与x的函数表达式;
(2)糖果销售单价定为多少元时,所获日销售利润最大,最大利润是多少?
(3)若超市决定每销售一盒糖果向儿童福利院赠送一件价值为m元的礼品,赠送礼品后,为确保该种糖果日销售获得的最大利润为392元,求m的值.
22.某广场建了一座圆形音乐喷水池,在池中心竖直安装一根水管,安装在水管顶端A处的圆形喷头向四周喷水,且各个方向喷出的抛物线形水柱形状相同.如图1,以池中心O点为坐标原点,水平方向为x轴,所在的直线为y轴,建立平面直角坐标系.x轴上的点C,D为水柱的落水点,若落地直径,使喷出的抛物线形水柱在与池中心的水平距离为处达到最高.
(1)求图1中右边抛物线的解析式;
(2)计划在图1中的线段上的点B处竖立一座雕像,雕像高,若想雕像不碰到水柱,请求出线段的取值范围;
(3)圆形水池的直径为,喷水造型会随着音乐节奏起伏而变化,从而产生一组不同的抛物线(如图2),若右侧抛物线顶点始终在直线上,当喷出的抛物线水柱最大高度为时,水柱会喷到圆形水池之外吗?请说明理由.
23.某次军训中,借助小山坡的有利地势,优秀学员小华在教官的指导下用手榴弹(模拟手榴弹)进行一次试投:如图所示,把小华投出的手榴弹的运路线看成一条开口向下的抛物线,抛物线过原点,手榴弹飞行的最大高度为10米,此时它的水平飞行距离为20米,山坡的坡度为,坡顶A处的水平距离为30米.
(1)求这条抛物线的函数解析式(不要求写出自变量的取值范围);
(2)小华投出的手榴弹能否越过坡顶A?请说明理由;
(3)若,坡上趴着几位“敌军”同学,手榴弹落地后会爆炸,爆炸后距落地点米范围内会受波及,问手榴弹落地爆炸后是否会波及斜坡?请说明理由.
24.某工厂生产某种玩具的成本价为36元件,工厂决定采取电商销售和门店销售两种方式销售该玩具.前20天电商销售:售价为62元件;后20天门店销售:第20天售价为62元件,此后售价每天比前一天每件降低0.5元.已知两种销售方式第天的销售数量(件均满足且为整数).
(1)求门店销售方式每天的售价y(元/件)与x的函数关系式;
(2)该玩具销售过程中,在第几天获得的利润W(元)最大?最大利润是多少?
(3)该玩具销售过程中,请直接写出日销售利润不低于3510元的天数.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.(1)
(2)①当销售单价时,该花店销售鲜花礼盒每天获得的利润为5000元;②销售单价时,花店销售该鲜花礼盒每天获得的利润最大,最大利润为6000元
【分析】本题考查二次函数的实际应用、一元二次方程的实际应用、一次函数的实际应用,理解题意,正确求得相关的函数关系式及方程是解答的关键.
(1)根据题意求解函数关系式即可;
(2)①根据利润销售总价成本价日均销售量×单件利润列方程求解即可;
②根据利润日均销售量×单件利润得到函数关系式,利用二次函数的性质求解即可.
【详解】(1)解:由题意,,
即与的函数关系式为;
(2)解:由题意,,
∴,
①根据题意,得,
整理,得,
解得,,
∵,,
∴,
答:当销售单价时,该花店销售鲜花礼盒每天获得的利润为5000元;
②由题意,,
∵,,
∴当时,y有最大值,最大值为,
答:销售单价时,花店销售该鲜花礼盒每天获得的利润最大,最大利润为6000元.
2.(1)横向甬道的面积为
(2)甬道的宽为
(3)所以当通道的宽度为8米时,所建花坛的总费用最少,最少费用是万元
【分析】本题考查了二次函数的应用,掌握梯形的面积公式及二次函数的性质是解题的关键.
(1)根据梯形的面积公式求解;
(2)根据“三条通道的面积是梯形露营地面积的八分之一”列方程求解;
(3)先根据费用等于面积乘以单价,列出函数关系式,再根据二次函数的性质求解.
【详解】(1)解:横向甬道的面积为:;
答:横向甬道的面积为;
(2)依题意:,
整理得:,
(不符合题意,舍去),
答:甬道的宽为;
(3)设建设花坛的总费用为y万元,
则:,
即:,
,
随x的增大而减小,
,
当米时,总费用最少.
即最少费用为:万元,
所以当通道的宽度为8米时,所建花坛的总费用最少,最少费用是万元.
3.(1)
(2)这一周该商场销售这种商品获得的最大利润为元,售价为12元/件
(3)
【分析】此题主要考查二次函数的实际应用,解题的关键是熟知待定系数法的应用、根据题意找到数量关系列出函数关系式.
(1)根据待定系数法即可求出一次函数的解析式;
(2)先根据题意求出x的取值,再由利润的关系列出利润为w关于x的二次函数,化为顶点式即可求解;
(3)根据题意可知,再根据对称轴的特点列出关于m的不等式,故可求解.
【详解】(1)解:设y与x的函数关系式为:,
把和代入得
,
解得,
∴;
(2)解:根据“在销售过程中要求销售单价不低于成本价,若某一周该商品的销售量不少于件,
得:
解得,,
设利润为w元,根据题意得,
,
∵,
∴当时,w随x的增大而增大,
∵,且x为正整数,
∴当时,w取最大值为:,
答:这一周该商场销售这种商品获得的最大利润为元,售价为12元;
(3)解:根据题意得,,
∴对称轴为,
∵,
∴当时,w随x的增大而增大,
∵该商场这种商品售价不大于17元/件时,捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.
∴,解得,
∵,
∴.
4.(1),
(2)
(3)当时,实验田的面积S最大,最大面积是
【分析】本题考查了矩形的性质,二次函数的实际应用,计算的取值范围是解题的关键.
(1)根据,求出与的函数解析式,根据矩形面积公式求出与的函数解析式;
(2)先求出的取值范围,再将代入函数中,求出的值;
(3)将与的函数配成顶点式,求出的最大值.
【详解】(1)解:,
,
,
;
(2),
,
,
,
当时,,
,
,
,
当时,矩形实验田的面积能达到;
(3),
当时,有最大值.
5.(1)
(2)每件消毒用品的售价为 13 元
(3)当每件消毒用品的售价为 15 元时, 最大利润是 525 元
【分析】(1)待定系数法求解即可;
(2)依题意,利润,令,则,计算求解满足要求的值即可;
(3)根据二次函数的性质以及的取值范围进行求解即可.
【详解】(1)解:设与的函数关系式为 ,
将 代入得,
解得,
,
与的函数关系式为;
(2)解:利润,
令,
则,
解得或(不合题意,舍去),
每件消毒用品的售价为 13 元;
(3)解:由(2)知,
,
当时,随着的增大而增大,
当时,,此时利润最大,
当每件消毒用品的售价为15元时, 最大利润是525元.
【点睛】本题考查了代行系数法求一次函数的解析式,一元二次方程的实际应用,二次函数的应用,二次函数的图象与性质.解题的关键在于对相关知识的熟练掌握与灵活运用.
6.(1)一盒果篮的成本为48元
(2)
(3)每月的最大利润为12960元
【分析】此题考查了分式方程的应用,二次函数的应用,二次函数的性质,正确理解题意列得方程及函数关系式是解题的关键.
(1)设A种水果的单价为a元,则B种水果的单价为元,根据用600元购进A种水果和用800元购进B种水果数量一样多列分式方程解答;
(2)根据利润=每盒果篮的利润×销量得到函数解析式;
(3)当且m为整数时,根据函数的性质求解即可.
【详解】(1)解:设A种水果的单价为a元,则B种水果的单价为元.
依题意,得,
解得:,
经检验,是原分式方程的解,,
∴一盒果篮的成本为:(元);
(2)解:依题意,得;
(3)解:由(2)可知每月的利润,
可化简为,
当且m为整数时,
∵,
∴当时w最大,此时:,
∴每月的最大利润为12960元.
7.(1)
(2),
(3)当售价是元件时,周销售利润最大,最大利润是元
【分析】本题考查了待定系数法求一次函数的解析式及二次函数在实际问题中的应用,理清题中的数量关系并明确二次函数的性质是解题的关键.
(1)设关于的函数解析式为,用待定系数法求解即可;
(2)该商品进价等于周销售利润除以周销售量,再减去进价;
(3)根据周销售利润周销售量售价进价,列出关于的二次函数,根据二次函数的性质可得答案.
【详解】(1)解:设关于的函数解析式为,将,分别代入得:
,
解得.
关于的函数解析式为.
(2)解:∵该商品进价是元件;
当时,,当时,元,
故答案为:,;
(3)解:由题意得:
二次项系数,抛物线开口向下,
当售价是元件时,周销售利润最大,最大利润是元.
8.(1)
(2)销售产品所获利润是0.75万元
(3)当销售量3吨时,获得最大利润,最大利润为10.5万元
【分析】本题考查的是二次函数的实际应用:
(1)根据题意可设抛物线为:,再把代入,即可求解;
(2)根据二次函数的性质可得当时,成本最小值为,此时,即可求解;
(3)设销售利润为W万元,根据题意可得W关于x的函数关系式,再根据二次函数的性质,即可求解.
【详解】(1)解:根据题意可设抛物线为:,
把代入可得:,
解得:,
∴抛物线的解析式为;
(2)解:∵,
∴当时,成本最小值为,
此时,
∴销售产品所获利润是(万元);
(3)解:设销售利润为W万元,根据题意得:
∴,
∵,
∴当时,W的值最大,最大值为10.5,
即当销售量3吨时,获得最大利润,最大利润为10.5万元.
9.(1)
(2)月销售量为,月销售利润为6750元
(3)销售单价为70元时,获得的利润最大,最大利润是9000元
【分析】本题主要考查了二次函数的应用,能正确表示出月销售量是解题的关键.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法.
(1)利润销售量单位利润,单位利润为,销售量为,据此表示利润得关系式;
(2)结合(1)计算即可;
(3)根据(1)中函数关系式,配方,利用二次函数的性质可得到总利润的最大值.
【详解】(1)解:根据题意得:,
∴y与x的函数解析式为;
(2)解:当时,销售量:,
销售利润:,
答:销售量为,销售利润为6750元;
(3)解:,
∵,
∴当时,利润最大为9000元.
答:销售单价为70元时,获得的利润最大,最大利润是9000元.
10.(1)65;90
(2)每件童装降价20元
(3)当每件童装降价25元时,每周盈利最多,最多盈利6050元
【分析】本题考查了一元二次方程及二次函数的应用,掌握平均每天售出的件数×每件盈利=每天销售的利润的运用是解题的关键,读懂题题意,找出之间的数量关系列出方程(或函数解析式)即可.
(1)根据降价后的利润=原利润-降的钱;根据每件童装降价5元,则每周可多售出10件,即可表示出每天的销售数量;
(2)设每件童装应降价x元,根据题目中的等量关系列出方程解方程即可;
(3)设每周销售这种童装利润为y,列出y与x的函数关系式,利用二次函数的性质解决问题即可.
【详解】(1)降价15元后,每件童装盈利是:元;
每周销售量是∶件.
故答案为:65;90;
(2)设每件童装应降价x元,根据题意得:
,
解得,(不合题意,舍去),
答:每件童装降价20元;
(3)设设每件童装应降价x元,每周销售这种童装利润为y元,根据题意得:
,
当时,函数有最大值6050.
答:当每件童装降价25元时,每周盈利最多,最多盈利6050元.
11.(1)篮球运行过程中的最大高度是;
(2)篮球落地时所运行的水平距离为;
(3)这次投球能命中
【分析】本题主要考查二次函数的应用和一元二次方程的应用,关键是利用二次函数的性质解答.
(1)把函数解析式化为顶点式,由函数的性质求最值;
(2)令,解方程即可;
(3)把代入解析式求出的值即可判断.
【详解】(1)解:
,
,
当时,有最大值,最大值为4,
答:篮球运行过程中的最大高度是;
(2)解:令,则,
整理得:,
解得(舍去),,
答:篮球落地时所运行的水平距离为;
(3)解:当时,,
点在抛物线上,
答:这次投球能命中.
12.(1)4000元
(2)
(3)销售单价为82元时,每天的销售利润最大,最大利润为4480.
【分析】本题主要考查的是二次函数的应用,依据题意列出每天的销售利润y与定价x的函数关系式是解题的关键.
(1)根据题意先求得当单价为70元时的销售量,然后根据利润=销售量×每件的利润求解即可;
(2)依据销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件列出函数关系式即可;
(3)每天的总成本每件的成本每天的销售量列出一元一次不等式,从而可求得x的范围,然后利用二次函数的性质可求得最大值即可.
【详解】(1)解:当销售单价为70元时,每天的销售利润元;
答:每天的销售利润是4000元
(2)解:由题得.
∵销售单价不得低于成本,
∴.且销量,
∴,解得,
∴.
∴
(3)解:∵该企业每天的总成本不超过7000元
∴,解得.
由(2)可知,
∵抛物线的对称轴为且,
∴抛物线开口向下,在对称轴右侧.
∴当时,y有最大,最大值为4480,即销售单价为82元时,每天的销售利润最大,最大利润为4480元.
13.(1)
(2)元
(3)元,元
【分析】(1)依题意设,待定系数法求解即可;
(2)当时,,当时,,根据,计算求解即可;
(3)设总收益为W元,则,由,可知当时,W有最大值,计算求解即可.
【详解】(1)解:依题意设,
将,代入得,,
解得,
∴.
(2)解:当时,,
当时,,
∴;
答:在政府未出台补贴措施之前,该商场销售彩电的总收益额为元.
(3)解:设总收益为W元,则,
∵,
∴当时,W有最大值.
答:政府应将每台补贴款额定为元时,可获得最大利润元.
【点睛】本题考查了一次函数解析式,一次函数的应用,二次函数的应用,二次函数的最值等知识.熟练掌握一次函数解析式,一次函数的应用,二次函数的应用,二次函数的最值是解题的关键.
14.(1)时,学生的接受能力逐步增强;时,学生的接受能力逐步降低
(2)
(3)
【分析】本题考查了二次函数的性质,解题的关键是掌握二次函数的性质.
(1)根据题意可得该二次函数开口向下,则函数图像在对称轴的左边随的增大而增大,在对称轴的右边随的增大而减小,据此即可求解;
(2)求出时的值即可求解;
(3)根据函数的性质可得函数在顶点处有最大值.
【详解】(1)解:函数中,,对称轴为直线,
当时,随的增大而增大,当时,随的增大而减小,
即 时,学生的接受能力逐步增强;时,学生的接受能力逐步降低;
(2)当时,,
故第分钟时,学生的接受能力是;
(3)当时,值最大,是,
故第分钟时,学生的接受能力最强.
15.(1)y关于x的函数解析式为
(2)制作该毕业相册的成本价为80元/套
(3)当售价是140元时,销售利润最大,最大利润是10800元
(4)这种毕业相册的售价为120元/套
【分析】本题考查待定系数法求函数解析式,一次函数和二次函数的实际应用,一元二次方程的实际应用.
(1)设y关于x的函数解析式为,代入表中相关数据得二元一次方程组,求解即可;
(2)设制作该毕业相册的成本价为m元/套,则,代入表中相关数据,得到关于m的方程,求解即可;
(3)根据每件的利润乘以销售量等于销售利润,得关于x的二次函数,根据二次函数的性质可得答案;
(4)根据“当所得利润为9600元”即可列出一元二次方程,求解并结合题意取舍即可解答.
【详解】(1)解:由题意可设y关于x的函数解析式为,
由表格可知当时,;当时,,
∴
解得:
∴y关于x的函数解析式为;
(2)设制作该毕业相册的成本价为m元/套
由题意可知:
由表可得当时,,,
∴,
解得:
∴制作该毕业相册的成本价为80元/套;
(3)解:由题意可知:
∵
∴当时,w有最大值,最大值为10800
答:当售价是140元时,销售利润最大,最大利润是10800元.
(4)解:当所得利润为9600元,即时,
,
解得:,,
∵由于影像公司尽可能让利于学生,
∴,
∴这种毕业相册的售价为120元/套.
16.(1)
(2)当销售单价定为元时,商场可获最大利润,最大利润是元
【分析】本题考查了二次函数的应用,熟练掌握二次函数的性质是解题关键.
(1)根据利润=销售量×(销售单价-成本)得到与之间的函数关系式,
(2)利用二次函数的性质结合已知条件求解即可.
【详解】(1)解:设销售量y(个)与销售单价x(元)一次函数关系为,
当时,;当时,.
,解得
,
∴
,
(2)解:,
,抛物线开口向下,在的左侧,随的增大而增大,
时,有最大值,最大值为元.
答:当销售单价定为元时,商场可获最大利润,最大利润是元.
17.(1)
(2)销售单价应定为每千克60元或70元
(3)当蟠桃售价每千克65元时,利润最大,最大利润是2500元
【分析】本题考查一次函数解析式,一元二次方程的实际应用,二次函数的实际应用.
(1)设y关于x的函数解析式为,根据当时,;当时,,利用待定系数法求解即可;
(2)根据利润销售量(售价进价)建立方程求解即可;
(3)设利润为,根据利润销售量(售价进价)建立函数关系式,利用二次函数的性质即可解答.
【详解】(1)解:设y关于x的函数解析式为,
根据题意得:,
解得:,
y关于x的函数解析式为;
(2)解:根据题意得:,即,
解得:,
答:销售单价应定为每千克60元或70元;
(3)解:设利润为,根据题意得:
,即,
,
,
当时,有最大值,最大值为,
答:当蟠桃售价每千克65元时,利润最大,最大利润是2500元.
18.(1)
(2)销售产品所获利润是万元;
(3)当销售量吨时,获得最大利润,最大利润为:万元;
【分析】(1)设抛物线为:,再利用待定系数法求解即可;
(2)先求解当时,成本的最小值为,再计算销售额,从而可得答案;
(3)设销售利润为万元,可得,再利用二次函数的性质解题即可;
【详解】(1)解:∵成本(万元)与销售量x(吨)的函数图象是如图所示的抛物线的一部分,其中是其顶点.
∴设抛物线为:,
把代入可得:,
解得:,
∴抛物线为;
(2)解:∵,
∴当时,成本最小值为,
∴,
∴销售产品所获利润是(万元);
(3)解:设销售利润为万元,
∴
,
当时,获得最大利润,
最大利润为:(万元);
【点睛】本题考查的是二次函数的实际应用,一次函数的应用,二次函数的性质,待定系数法的含义,熟练的建立二次函数的关系式是解本题的关键.
19.(1)米
(2)不能,理由见详解
(3)108
【分析】本题考查了一元二次方程的应用和二次函数的性质.
(1)根据各边之间的关系,可知为米,根据围成的菜地面积为平方米,可得出关于的一元二次方程,解之取其符合题意的值即可;
(2)根据菜地面积若为平方米,即可得出关于的一元二次方程,利用根的判别式即可判断;
(3)利用二次函数的性质求其最大值即可.
【详解】(1)解:∵篱笆的总长为米,菜地的前端各设计了两个宽米的小门,且垂直于墙的篱笆边为米,
∴长为米.
根据题意得:,
整理得:,
解得:,,
当时,,不符合题意,舍去;
当时,,符合题意;
故当围成的菜地面积为平方米时,为米.
(2)解:不能围成面积为平方米的菜地,理由如下:
依题意得:,
整理得:,
∵,
∴该方程无实数根,
即不能围成面积为平方米的菜地.
(3),
则当时,,
故围成菜地的最大面积为108平方米.
20.(1)400;
(2)当时,取最大值,最大值为8750元;
(3)小红错误,理由见详解.
【分析】本题考查了二次函数的应用,一元一次不等式组的应用,一次函数的应用,熟练掌握知识点,正确理解题意是解题的关键.
(1)根据每盒售价每提高1元,每天要少卖出10盒,可以得到与之间的函数关系式,把代入解析式计算即可;
(2)根据每盒利润销售盒数总利润可得关于的关系式,由二次函数性质可得答案;
(3)根据题意,在正确的的范围中求出日销售额的最大值,判断小强是否正确,根据题意列出不等式,结合的范围求出不等式的解集,判断小红是否正确.
【详解】(1)解:由题意可得,
,
即每天的销售量(盒与每盒售价(元之间的函数关系式是,
当时,,
故答案为:400.
(2)解:由题意可得,
,
由题可知:每盒售价不得少于50元,日销售量不低于350盒,
,
即,解得.
当时,取得最大值,此时,
答:当每盒售价定为65元时,每天销售的利润(元最大,最大利润是8750元;
(3)解:小强:,
设日销售额为元,
,
当时,值最大,此时,
当时,值最大,此时,
小强正确.
小红:当日销售利润不低于8000元时,
即,
,解得:,
,
当日销售利润不低于8000元时,.
故小红错误,当日销售利润不低于8000元时,.
21.(1)
(2)糖果销售单价定为25元时,所获日销售利润最大,最大利润是450元
(3)2
【分析】本题考查了二次函数的应用,解题的关键是:
(1)利用待定系数法求解即可;
(2)设日销售利润为w元,根据利润=单件利润×销售量求出w关于x的函数表达式,然后利用二次函数的性质求解即可;
(3)设日销售利润为w元,根据利润=单件利润×销售量-m×销售量求出w关于x的函数表达式,然后利用二次函数的性质求解即可.
【详解】(1)解∶设y与x的函数表达式为,
把,;,代入,得,
解得,
∴y与x的函数表达式为;
(2)解:设日销售利润为w元,
根据题意,得
,
∴当时,有最大值为450,
∴糖果销售单价定为25元时,所获日销售利润最大,最大利润是450元;
(3)解:设日销售利润为w元,
根据题意,得
,
∴当时,有最大值为,
∵糖果日销售获得的最大利润为392元,
∴,
化简得
解得,
当时,,
则每盒的利润为:,舍去,
∴m的值为2.
22.(1)
(2)
(3)水柱会落在圆形水池外,理由见解析
【分析】本题考查的知识点是待定系数法求解析式、二次函数的实际应用,解题关键是理解题意求出正确的二次函数解析式.
(1)求出点和顶点坐标为,设顶点式,利用待定系数法解答即可;
(2)将代入即可求得线段的取值范围;
(3)求出点坐标,由题意设右侧喷出的最高抛物线解析式为,求出坐标解析式后可求抛物线喷出的最远距离,即可判断水柱是否会喷到圆形水池之外.
【详解】(1)解: ,
,
,
∵喷出的抛物线形水柱在与池中心的水平距离为处达到最高.
∴顶点坐标为,
设右侧抛物线的解析式为:,
把代入得到,,
解得,
∴图1中右边抛物线的解析式为;
(2)解:当时,,
解得(不合题意,舍去)
∴线段的取值范围为;
(3)解:水柱会落在圆形水池外,理由如下:
当时,,
∴点A的坐标为,
把代入
,
,
当右侧喷出的抛物线最大高度为时,
设抛物线的解析式为:,
又上述抛物线过点,则
则,
,
当时,,
,
,(舍去),
水柱会落在圆形水池之外.
23.(1)
(2)小华投出的手榴弹能越过坡顶,见解析
(3)手榴弹落地爆炸后不会波及斜坡,见解析
【分析】本题是二次函数的应用,关键是利用待定系数法求二次函数的解析式.
(1)根据顶点坐标和过原点求出抛物线的解析式;
(2)先利用坡度求出,再根据二次函数关系式求出当时,的值,再进行比较即可;
(3)令,解方程求出手榴弹落地点到原点的距离,再利用勾股定理求出,从而求出,然后用与比较即可.
【详解】(1)解:由题意得:顶点,且抛物线过原点,
所以设抛物线的解析式为:,
把代入得:,
解得,
∴抛物线的解析式为:;
(2)小华投出的手榴弹能越过坡顶,
理由:
由(1)知,
当时,,
∵山坡的坡度为米,
∴米,
∵,
∴小华投出的手榴弹能越过坡顶;
(3)手榴弹落地爆炸后不会波及斜坡,
理由:
令,则,
解得,
∴手榴弹的落地点距离原点040米,
∵米,米,
∴(米),
∴(米),
∵,
∴手榴弹落地爆炸后不会波及斜坡.
24.(1)
(2)第32天时利润最大,为4000元
(3)日销售利润不低于3510元的天数为22天
【分析】(1)门店销售方式每天的售价第20天的售价超过20天的天数;
(2)时,电商销售的利润电商销售每件玩具的利润销售量,进而根据函数的增减性和自变量的取值范围可得对应天数及此范围内的最大利润;当时,门店销售的利润门店销售每件玩具的利润销售量,整理成顶点式,可得此范围内的对应的天数及最大利润,比较后可得最大利润及对应天数;
(3)当时,令,求得的取值范围可得相应的天数;当时,令,求得的取值范围可得相应的天数,综合两种情况可得日销售利润不低于3510元的总天数.
本题考查一次函数的应用、二次函数的应用.分电商销售和门店销售两种情况探讨函数的最大值及日销售利润不低于3510元的天数是解决本题的难点.
【详解】(1)解:依题意,∵前20天电商销售:售价为62元件;后20天门店销售:第20天售价为62元件,此后售价每天比前一天每件降低0.5元
∴
.
(2)解:①当时,
.
,
随的增大而增大,
当时,最大.的最大值为:元;
②当时,
.
,
当时,有最大值4000元,
,
第32天时利润最大,为4000元.
(3)解:由(2)知,当时,
,
解得:,
共有2天;
当时,
,
,
,共20天,
综上,日销售利润不低于3510元的天数为22天.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
