人教版九年级上册数学第二十一章一元二次方程应用题训练(含解析)
文档属性
| 名称 | 人教版九年级上册数学第二十一章一元二次方程应用题训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-11 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
人教版九年级上册数学第二十一章一元二次方程应用题训练
1.某工厂使用旧设备生产,每月生产收入是90万元,每月另需支付设备维护费5万元从今年1月份起使用新设备,生产收入提高且无设备维护费,使用当月生产收入达100万元,1至3月份累计收入达364万元,且2,3月份的生产收入保持相同的增长率,3月份后每月生产收入稳定在3月份的水平.
(1)求使用新设备后,2月3月生产收入的月增长率
(2)购进新设备需一次性支付640万元,则使用新设备几个月后,该厂所得累计利润不低于使用旧设备的累计利润?(累计利润是指累计生产收入减去旧设备维护费或新设备购进费)
2.我校新城校区新建一个三层停车楼,每一层布局如图所示.已知每层长为50米,宽20米.阴影部分设计为停车位,其余部分是等宽的通道,已知喷漆面积为736平方米.
(1)求通道的宽是多少米?
(2)据调查分析,停车场多余64个车位可以对外出租,当每个车位的月租金为200元时;当每个车位的月租金每上涨10元,就会少租出1个车位,既能优惠大众,又能使对外开放的月租金收入为14400元?
3.为防控“新冠”疫情,我巴南区启动新冠疫苗加强针接种工作.已知今年5月甲接种点平均每天接种加强针的人数比乙接种点平均每天接种加强针的人数多30%,两接种点平均每天共有460人接种加强针.
(1)求5月平均每天分别有多少人前往甲、乙两接种点接种加强针?
(2)6月份,甲接种点平均每天接种加强针的人数比5月少人,乙接种点平均每天接种加强针的人数比5月多20%,在天期间,甲、乙两接种点共有2250人接种加强针,求的值.
4.果农李明种植的草莓计划以每千克15元的单价对外批发销售,由于部分果农盲目扩大种植,造成该草莓滞销.李明为了加快销售,减少损失,对价格经过两次下调后,以每千克元的单价对外批发销售.
(1)求李明平均每次下调的百分率;
(2)小刘准备到李明处购买3吨该草莓,因数量多,李明决定再给予两种优惠方案以供其选择:方案一:打九折销售;方案二:不打折,每吨优惠现金400元.试问小刘选择哪种方案更优惠,请说明理由.
5.某农场要建一个长方形的养鸡场,鸡场的一边靠墙,(墙长)另外三边用木栏围成,木栏长.
(1)设平行于墙的一边长为x,垂直于墙的一边y,求y与x的函数关系式.
(2)若养鸡场面积为200平方米,求鸡场垂直于墙的一边长.
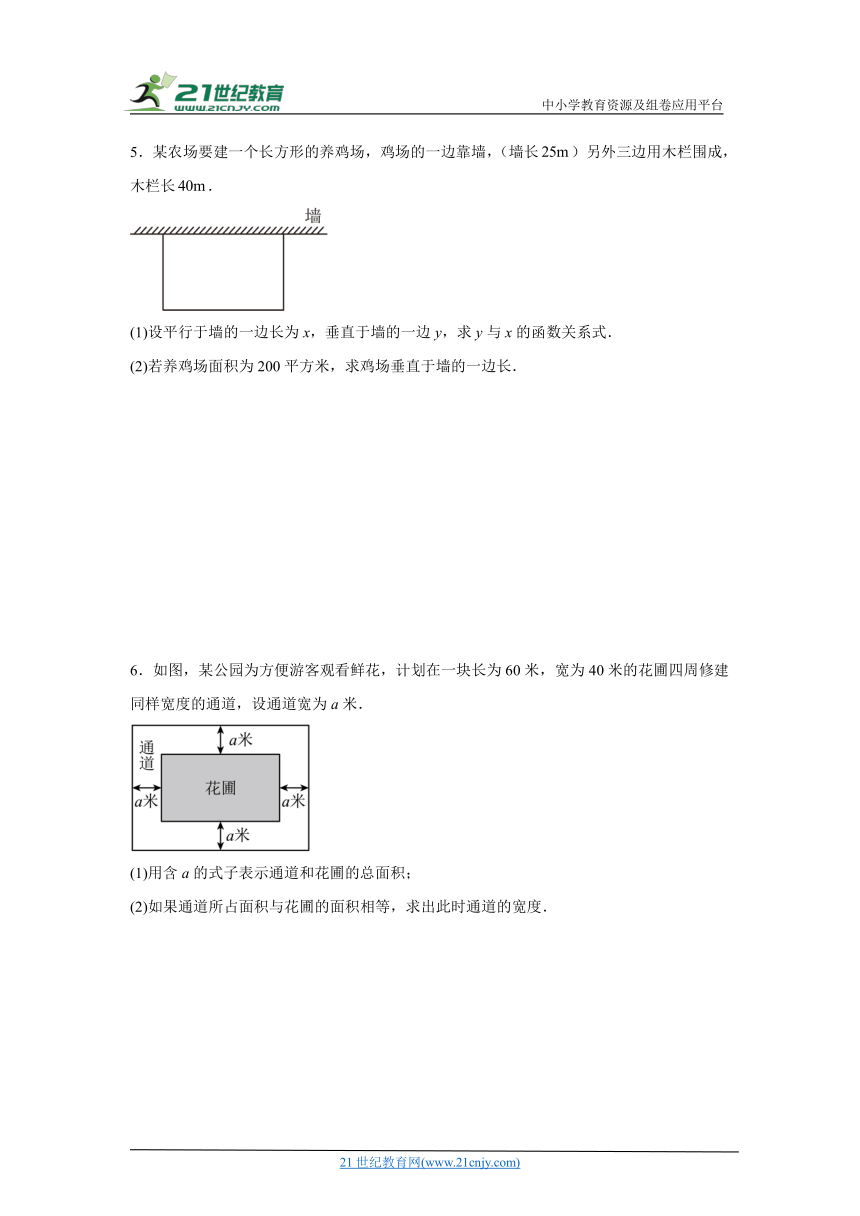
6.如图,某公园为方便游客观看鲜花,计划在一块长为60米,宽为40米的花圃四周修建同样宽度的通道,设通道宽为a米.
(1)用含a的式子表示通道和花圃的总面积;
(2)如果通道所占面积与花圃的面积相等,求出此时通道的宽度.
7.奥运会前夕,某超市在销售中发现:奥运会小饰品平均每天可售出200套,每件盈利20元.为了迎接奥运会,商场决定采取适当的降价措施,经市场调查发现:如果每套降价1元,那么平均每天就可多售出10套.
(1)当每套降价x元时,设每天销售数量为W,请直接写出W与x的函数关系式.
(2)要想平均每天在销售吉祥物上盈利3750元,那么每套应降价多少元?
8.如图,在一个边长为的正方形的四个角上分别剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),剩余的部分可以折成一个有盖的长方体盒子(纸板的厚度忽略不计),且折成的长方体盒子表面积是,设小正方形的边长为.
(1)请用x表示长方体的底面长和宽;
(2)长方体盒子的体积为多少?
9.如图,长方体的底面积为,长、宽、高的比为,则:
(1)这个长方体的长、宽、高分别是多少?
(2)长方体的表面积和体积分别是多少?
(3)若一只蚂蚁从顶点A沿长方体表面爬行到顶点B,直接写出从点A爬行到点B的最短路程是 .
10.某老牌造车企业为实现企业绿色低碳发展,通过技术改造升级,使新能源汽车项目的生产规模不断扩大,该企业9月,10月一共生产新能源汽车95000辆,其中10月份新能源汽车产量是9月份的倍少4000辆.(说明:生产的新能源汽车全部销售出去).
(1)求9月,10月新能源汽车产量各是多少辆
(2)若10月份每辆新能源汽车的利润为1万元,11月份新能源汽车产量比上月增加,11月份每辆新能源汽车的利润比上月增加,则11月份新能源汽车总利润达到66000万元,求m的值.
11.水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,这种水果每斤的售价每降低0.1元,每天可多售出20斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
12.近年来,电商平台直播带货成了一个火热的新兴职业,某主播带货图书《苏东坡传》,他用双语直播,风趣幽默,点燃了不同年龄者的读书热情.已知这本书的成本价为10元,规定销售单价不低于成本价,且不高于成本价的3倍,通过前几天的销售发现,该书每天的销售量y(本)与销售单价x(元/本)之间近似满足一次函数关系,部分对应数据如表:
x(元/本) … 15 25 …
y(本) … 600 400 …
(1)直接写出y关于x的函数关系式;
(2)若销售该书每天的利润为5000元,求该书的销售单价;
(3)销售该书每天的利润能否达到8000元?请说明理由.
13.振华商厦准备在月月销售一种多功能手机专用包,计划从厂家以每个元的价格进货,经过市场营销调查发现当每个手机专用包的售价为元时,月均销量为个,售价每增长元,月均销量就相应减少个.
(1)若使这种手机专用包的月均销量不低于个,每个手机专用包售价应不高于多少元?
(2)在()的条件下,当这种手机专用包销售单价为多少元时,月销售利润是元?
14.把一个足球垂直地面向上踢,t秒后该足球的高度h米适用公式,已知当足球踢出后4秒回到地面.
(1)求a的值.
(2)若该足球踢出t秒后和秒后,足球的高度相同,求t的值.
(3)是否有可能该足球踢出秒后的高度比踢出t秒后的高度高18米?通过计算说明.
15.某品牌纪念品每套成本为30元,当售价为40元时,平均每天的销售量为500套,经试销统计发现,如果该品牌纪念品售价每上涨1元,那么平均每天的销售量将减少10套,为了维护消费者利益,物价部门规定:该品牌纪念品售价不能超过进价的200%.设这种纪念品每套上涨x元.
(1)平均每天的销售量为______套(用含x的代数式表示):
(2)商家想要使这种纪念品的销售利润平均每天达到8000元,求每套纪念品应定价多少元?
16.士宝精品店以每件21元的价格购进一批商品,该商品可以自行定价,若每件商品售价为元,则可卖出件,但物价局限定每件商品的利润不得超过
(1)若商店计划要盈利400元,需要进货多少件?每件商品的售价应定为多少?
(2)在(1)的条件下,在实际销售的过程中,先将(1)中购进的商品卖出了部分后,决定将剩余商品打9折甩货,则至少先卖出多少件商品后再甩货才能保证利润不低于300元?
17.某商场销售一种学生用的计算器,进价为每台20元,售价为每台30元,每周可卖160台.根据市场调查,发现如果每台计算器的售价每上涨1元,每周就会少卖10台,但厂家规定最高每台售价不能超过33元.
(1)设每台售价上涨x元,每周的销售量为y台,则y与x之间的函数关系式为______;
(2)当计算器售价为多少元时,商场每周的利润恰好为1680元?(主要步骤列方程解答)
18.商场某种商品平均每天可销售件,每件盈利元.为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多售出2件,设每件商品降价x元,据此规律,请回答:
(1)商场日销售量增加______件,每件商品盈利(______)元;(用含x的代数式表示)
(2)在上述条件不变,销售正常情况下,每件商品降价多少元时,商场日盈利可达到元.
19.某商场经营一种成本为每千克40元的产品.
(1)已知四月份该产品的销售量为,经过适当调价后,6月份该产品的销量为,求月份该产品销售的月平均增长率.
(2)经市场调查发现,当该产品的售价为每千克50元时,月销售量为,每千克售价每涨价1元,月销售量将减少,该商场计划在月销售成本不超过10000元的情况下,要使月销售利润达到8000元,问销售该产品时每千克应涨多少元?
20.随着气温的逐步升高,空调成为了许多家庭的必需品,某商场最新推出的A、B两款空调凭借出色的性价比、智能互联功能以及时尚简约的设计风格,迅速赢得了年轻消费群体的青睐,已知A款空调的售价比B款空调的售价高600元,某商场在5月份销售了80台A款空调和100台B款空调,销售总金额为264000元.
(1)求A、B两款空调的销售单价分别为多少元?
(2)6月份的气温持续升高,商场抓住商机,对A款空调进行优惠促销,销售单价在5月份的基础上下降了m元,销售的数量比5月份增加了台,B款空调的销售单价不变,最终6月份两款空调一共销售了230台,销售金额比5月份增加了60000元.求m的值.
21.端午节吃粽子是中国人民的传统习俗.五月初利民副食店购进鲜肉粽、蜜枣粽两种粽子,其中鲜肉粽进价为15元/袋,售价为27元/袋,蜜枣粽进价为10元/袋,售价为19元/袋.利民副食店用660元购进鲜肉粽、蜜枣粽两种粽子共50袋.(注:利润=售价-进价)
(1)求购进鲜肉粽、蜜枣粽各多少袋?
(2)临近端午节,蜜枣粽售完,鲜肉粽还有剩余.副食店决定端午节当天对鲜肉粽降价销售,如果按原价销售,平均每天可售2袋.经调查发现,鲜肉粽每降价1元,平均每天可多售2袋.剩余的鲜肉粽在降价当天全部售完,50袋粽子共获利506元,每袋鲜肉粽应降价多少元?
22.第31届世界大学生夏季运动会在成都举办,其中大运会吉祥物蓉宝广受欢迎,成为热销商品.某商家以每套40元的价格购进一批蓉宝.当该商品每套的售价是50元时,每天可售出180套,若每套的售价每提高2元,则每天少卖4套.设蓉宝每套的售价定为x 元,该商品销售景y 套
(1)求y 与 x 之间的函数关系式;
(2)若每天销售所获的利润为4800元,求x的值.
23.“今天立夏,过来吃碗三虾面.”在百年老字号裕面堂内,一位老苏州说,苏州人立夏传统“尝三鲜”是蚕豆、苋菜、蒜苗,今年立夏提前吃碗夏令三虾面尝尝鲜.为了抓住这一商机,两商户决定生产预制面.据统计,甲商户每小时生产600包,乙商户每小时生产800包,甲乙两商户每天共生产16小时,且每天生产的三虾面总包数为11400包.
(1)甲、乙两商户每天分别生产多少小时?
(2)由于三虾面在网上直播热销,客户纷纷追加订单,两商户每天均增加了生产时间,其中甲商户比乙商户多增加2小时,在整个生产过程中,甲商户每小时产量不变,而乙商户由于机器损耗及人员不足,每增加一个小时,每小时产量将减少140包,这样两商户一天生产的面条总量将比原来多1200包.求:甲商户增加的生产时间为多少小时?
24.重庆市自发布“重庆市长江10年禁鱼通告”后,忠县内的黄钦水库自然生态养殖鱼在市场上热销,并被誉为“清凉五月天,黄钦自有贤”的美誉2024年五一假期依依同学旅游到此,并购买了若干桂花鱼和大罗非,她用840元买的桂花鱼的数量比用同样价钱买大罗非的数量多20斤,且大罗非的单价是桂花鱼的1.5倍,
(1)求桂花鱼、大罗非两种鱼的单价分别为多少元;
(2)两种鱼在得到一致好评后,依依决定再次购买这两种鱼作为“伴手礼”.由于商家对老顾客让利,其中桂花鱼按照原单价购买,大罗非的单价每斤降低m元,则购买的数量会比第一次购买大罗非的数量增加2m斤,第二次一共购买80斤鱼共用了1340元.求m的值.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.(1)每月的增长率是.
(2)使用新设备12个月后,该厂所得累计利润不低于使用旧设备的累计利润.
【分析】本题主要考查理一元二次方程的应用、一元一次不等式的应用等知识点,根据题意列出方程和不等式是解题的关键.
(1)设每月的增长率为x,那么2月份的生产收入为,三月份的生产收入为,根据1至3月份的生产收入累计可达364万元可列方程求解即可;
(2)设使用新设备y个月后,该厂所得累计利润不低于使用旧设备的累计利润,根据不等关系可列不等式求解即可.
【详解】(1)解:设每月的增长率为x,由题意得:,
解得或(不合题意舍去).
答:每月的增长率是.
(2)解:设使用新设备y个月后,该厂所得累计利润不低于使用旧设备的累计利润,依题意有,
解得.
答:使用新设备12个月后,该厂所得累计利润不低于使用旧设备的累计利润.
2.(1)通道的宽是2米
(2)每个车位的月租金应上涨40元
【分析】本题考查了一元二次方程的实际应用,解题的关键是设未知数,找出等量关系,正确列出方程.
(1)设通道的宽是x米,则每一层的停车位可合成长为米,宽为米的矩形,再根据喷漆面积列出方程求解即可;
(2)设每个车位的月租金上涨y元,则每个车位的月租金为元,少租出个车位,再根据月租金列出方程求解即可.
【详解】(1)解:设通道的宽是x米,则每一层的停车位可合成长为米,宽为米的长方形,
依题意得:,
整理得:,
解得:,(不符合题意,舍去).
答:通道的宽是2米.
(2)解:设每个车位的月租金上涨y元,则每个车位的月租金为元,少租出个车位,
依题意得:,
整理得:,
解得:,,
又∵要优惠大众,
.
答:每个车位的月租金应上涨40元.
3.(1)5月平均每天有260人前往甲接种点接种,200人前往乙接种点接种加强针
(2)的值为5
【分析】本题考查了一元一次方程的应用以及一元二次方程的应用,解题的关键是:找准等量关系,正确列出方程.
(1)设5月平均每天有人前往乙接种点接种加强针,则可以表示出前往甲接种点接种的人数,再根据两接种点的总人数列出方程即可;
(2)由5月份和6月份甲、乙两接种点的每天接种人数关系可以求出6月份的站点接种人数,再根据总的接种人数列出一元二次方程求解,此时解得的值有两个,再根据6月份甲接种点的人数判断值的取舍.
【详解】(1)解:设5月平均每天有人前往乙接种点接种加强针,则5月平均每天有人前往甲接种点接种,
由题意得:,
解得:,
∴人.
答:5月平均每天有260人前往甲接种点接种,200人前往乙接种点接种加强针;
(2)由题意得:6月平均每天有人前往甲接种点接种,有人前往乙接种点接种,
,
解得,
当时,,符合题意;
当时, ,不符合题意,舍去.
答:a的值为5.
4.(1)
(2)方案一,理由见解析
【分析】本题主要考查了一元二次方程的实际应用,有理数乘法的实际应用:
(1)设平均每次下调的百分率为x,根据经过两次下调后,以每千克元的单价对外批发销售列出方程求解即可;
(2)根据所给优惠方案分别求出两个方案的费用即可得到答案.
【详解】(1)解:设平均每次下调的百分率为x,
由题意,得,
解这个方程,得,
∵降价的百分率不可能大于1,
∴不符合题意,
符合题目要求的是,
答:平均每次下调的百分率是.
(2)解:小刘选择方案一购买更优惠,
理由:方案一所需费用为:(元),
方案二所需费用为:(元),
∵,
∴小刘选择方案一购买更优惠.
5.(1)
(2)
【分析】本题考查列一次函数解析式、一元二次方程的应用,(1)根据题意求解即可;
(2)根据长方形的面积公式列方程求解即可.
【详解】(1)解:由题意得,;
(2)解:由题意得,,
解得,
∴,
答:鸡场垂直于墙的一边长为.
6.(1)平方米
(2)10米
【分析】本题考查一元二次方程的实际应用:
(1)根据题意,得到总面积为长为,宽为的长方形的面积,列出代数式即可;
(2)根据题意,列出一元二次方程,进行求解即可.
【详解】(1)解:由题意,得,总面积为:平方米;
(2)由题意,得:,
解得:或(舍去);
∴通道的宽度为10米.
7.(1)
(2)每套应降价元
【分析】本题考查一元二次方程的运用,写出函数解析式,关键是看到降价和销售量的关系,然后根据利润可列方程求解.
(1)根据题干中降价和销售量的关系,写出函数解析式,即可解题;
(2)根据“平均每天在销售吉祥物上盈利3750元”列出方程求解,即可解题.
【详解】(1)解:根据题意可知;
(2)解:根据题意可知,
整理得,
解得,(舍去),
答:每套应降价元.
8.(1)长为,宽
(2)
【分析】本题考查了一元二次方程的应用、正方形与长方形面积的计算等知识,正确理解题意,找准数量关系列出一元二次方程是解题的关键.
(1)设剪去小正方形的边长为,则折成的长方体盒子的底面的长为,宽为;
(2)剩余的部分折成的长方体盒子的表面积是,列出一元二次方程,解方程即可.
【详解】(1)解:设剪去小正方形的边长为,
则折成的长方体盒子的底面的长为,宽为;
(2)解:由题意得:,
整理得:,
解得:或(不符合题意,舍去),
剪去小正方形的边长为,
长方体盒子的体积是,
则长方体盒子的体积为.
9.(1)这个长方体的长、宽、高分别是
(2)这个长方体的体积为,表面积为
(3)
【分析】本题考查了一元二次方程的实际应用,平面展开-最短路线问题,勾股定理应用.“化曲面为平面”是解决“怎样爬行最近”这类问题的关键.
(1)设这个长方体的长、宽、高分别是,根据长方体的底面积为,建立方程求解即可;
(2)由(1)中结果列式计算即可;
(3)把此长方体的一面展开,然后在平面内,利用勾股定理求点A和B点间的线段长,即可得到蚂蚁爬行的最短距离.应该是前面和上面展开,利用勾股定理可求得.
【详解】(1)解:设这个长方体的长、宽、高分别是,根据题意得:
,即,
(负值舍去)
这个长方体的长、宽、高分别是;
(2)解:由(1)知这个长方体的长、宽、高分别是,
这个长方体的体积为:,
这个长方体的表面积为:;
(3)解:平面展开图不唯一,故分情况分别计算,进行大、小比较,再从各个路线中确定最短的路线.
展开前面上面,由勾股定理得;
展开前面右面,由勾股定理得;
展开前面和左面,由勾股定理得.
,
最短路径的长为.
10.(1)9月新能源汽车的产量为45000辆,10月新能源汽车的产量为50000辆;
(2)m的值为20.
【分析】本题考查了一元一次方程的应用以及一元二次方程的应用,找准等量关系,正确列出方程是解题的关键.
(1)设9月新能源汽车的产量为x辆,则10月新能源汽车的产量为辆,根据该厂9,10月共生产新能源汽车95000辆,即可得出关于x的一元一次方程,解之即可求出x的值,再将其代入中即可求出10月新能源汽车的产量;
(2)利用月利润=每辆的利润×月产量,即可得出关于m的一元二次方程,解之取其正值即可得出结论.
【详解】(1)解:设9月新能源汽车的产量为x辆,则10月新能源汽车的产量为辆,
依题意得:,
解得:,
∴.
答:9月新能源汽车的产量为45000辆,10月新能源汽车的产量为50000辆;
(2)解:依题意得:,
整理得:,
解得:,(不合题意,舍去).
答:m的值为20.
11.(1)
(2)张阿姨需将每斤的售价降低1元或0.5元
【分析】本题考查理解题意的能力,第一问关键求出每千克的利润,求出总销售量,从而利润.第二问,根据售价和销售量的关系,以利润作为等量关系列方程求解.
(1)销售量原来销售量下降销售量,据此列式即可;
(2)根据销售量每斤利润总利润列出方程求解即可.
【详解】(1)将这种水果每斤的售价降低元,则每天的销售量是(斤,
故答案为:;
(2)根据题意得:,
解得:或,
答:张阿姨需将每斤的售价降低1元或0.5元.
12.(1)
(2)20元
(3)销售该书每天的利润不能达到8000元,理由见解析
【分析】本题考查一次函数的实际应用,一元二次方程的实际应用.掌握利用待定系数法求一次函数解析式和理解题意,找出等量关系,列出方程是解题关键.
(1)设y关于x的函数关系式为,再利用待定系数法求解即可;
(2)根据题意可列出关于x的一元二次方程,求解,再舍去不合题意的解即可;
(3)根据题意可列出关于x的一元二次方程,根据其根的判别式小于0,可判断其无解,即说明销售该书每天的利润不能达到8000元.
【详解】(1)解:设y关于x的函数关系式为,
根据题意得:,
解得:.
∵规定销售单价不低于成本价,且不高于成本价的3倍,
∴,
∴y关于x的函数关系式为;
(2)解:根据题意得:,即,,
整理得:,
解得:,(舍),
答:该书的销售单价为20元;
(3)解:根据题意得:,即,,
整理得:,
∵,
∴原方程无解,
∴销售该书每天的利润不能达到8000元.
13.(1)每个手机专用包售价应不高于元;
(2)当该这种手机专用包销售单价为元时,销售利润是元.
【分析】()设每个手机专用包售价为元,根据题意列出,然后求解即可;
()由题意列方程,然后解方程检验即可;
本题主要考查了一元二次方程的应用,一元一次不等式的应用,明确题意,准确得到数量关系是解题的关键.
【详解】(1)设每个手机专用包售价为元,
依题意得:
解得:,
∴的最大值为,
∴每个手机专用包售价应不高于元;
(2)依题意得:
整理得:,
解得:,(不符合题意,舍去),
∴当该这种手机专用包销售单价为元时,销售利润是元.
14.(1)20
(2)
(3)没有可能,计算见解析
【分析】本题考查了一元二次方程的应用,熟练掌握知识点,正确理解题意是解题的关键.
(1)取,代入公式可得的值;
(2)由踢出t秒后和秒后,足球的高度相同得,解方程即可;
(3)求得自变量为和时的函数值,相减为18,看求得的是否符合题意即可.
【详解】(1)解:由题意得:当时,.
.
解得:;
(2)解:由(1)得:,
∵踢出t秒后和秒后,足球的高度相同
∴,
解得:;
(3)解:由题意得:.
.
解得:(不合题意,舍去).
没有可能该足球踢出秒后的高度比踢出秒后的高度高18米.
15.(1)
(2)每套纪念品应定价50元.
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
(1)由题意即可得出结论;
(2)设这种纪念品每套上涨元,则每套纪念品应定价为元,平均每天的销售量为套,根据这种纪念品的销售利润平均每天达到8000元,列出一元二次方程,解之取符合题意的值即可.
【详解】(1)解:由题意可知,平均每天的销售量为套,
故答案为:;
(2)解:设这种纪念品每套上涨元,则每套纪念品应定价为元,平均每天的销售量为套,
由题意得:,
整理得:,
解得:,(不符合题意,舍去),
,
答:每套纪念品应定价50元.
16.(1)需要进货100件,每件商品应定价25元
(2)至少先卖出60件商品后再甩货才能保证利润不低于300元
【分析】本题考查了一元二次方程的应用及一元一次不等式的应用,熟练掌握利润的计算方法是解题的关键.
(1)利润=售价-进价,总利润=单件利润×总件数,注意限制条件的作用.
(2)设先卖出m件商品后再甩货才能保证利润不低于300元,根据题意列出不等式解决即可.
【详解】(1)解:依题意,
整理得,
解得,.
因为,
所以不合题意,舍去.
所以(件).
答:需要进货100件,每件商品应定价25元.
(2)设先卖出m件商品后再甩货才能保证利润不低于300元,由题意得:
,
解得:,
至少先卖出60件商品后再甩货才能保证利润不低于300元.
17.(1)
(2)当计算器定价为32元时,商场每周的利润恰好为1680元.
【分析】本题考查的是一次函数的实际应用,一元二次方程的实际应用,理解题意是解本题的关键;
(1)由实际销售量等于原来销量减去减少的销量即可得到关系式;
(2)由每件计算器的利润乘以销售数量建立方程求解即可;
【详解】(1)解:由题意可得:;
(2)解:由题意可得:,
∴,
解得,,,
∵,
∴符合题意,
∴此时计算器的售价为(元),
即当计算器定价为32元时,商场每周的利润恰好为1680元.
18.(1),
(2)元
【分析】本题考查了列代数式,一元二次方程的应用.熟练掌握列代数式,一元二次方程的应用是解题的关键.
(1)由题意知,每件商品降价x元,商场日销售量增加件,每件商品盈利元;
(2)依题意得,,整理得,,计算求出满足要求的解即可.
【详解】(1)解:由题意知,每件商品降价x元,商场日销售量增加件,每件商品盈利元,
故答案为:,;
(2)解:依题意得,,整理得,,
,
解得,或,
∵为了尽快减少库存,
∴,
∴每件商品降价元时,商场日盈利可达到元.
19.(1)月份该产品销售的月平均增长率为
(2)销售该产品时每千克应涨30元
【分析】此题考查的是一元二次方程的应用,读懂题意,找到合适的等量关系,然后设出未知数正确列出方程是解题的关键.
(1)设月份该产品销售的月平均增长率为x,列方程并解方程即可解决;
(2)根据销售单价每涨价1元,月销售量就减少10千克,结合月销售利润=每件利润×数量即可列出方程,解方程即可;
【详解】(1)解:设月份该产品销售的月平均增长率为x,由题意得:
,
解得:(不合题意舍去),
答:月份该产品销售的月平均增长率为;
(2)解:设销售该产品时每千克应涨y元,
,
解得:,
当时,月销售成本为,不合题意舍去,
当时,月销售成本为,符合题意,
∴,
答:销售该产品时每千克应涨30元.
20.(1)款空调的销售单价为1800元,款空调的销售单价为1200元
(2)的值为200
【分析】本题考查了一元二次方程的应用以及二元一次方程组的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)找准等量关系,正确列出一元二次方程.
(1)设款空调的销售单价为元,款空调的销售单价为元,根据款空调的售价比款空调的售价高600元,某商场在5月份销售了80台款空调和100台款空调,销售总金额为264000元.列出二元一次方程组,解方程组即可;
(2)根据最终6月份两款空调一共销售了230台,销售金额比5月份增加了60000元.列出一元二次方程,解之取符合题意的值即可.
【详解】(1)解:设款空调的销售单价为元,款空调的销售单价为元,
由题意得:,
解得:,
答:款空调的销售单价为1800元,款空调的销售单价为1200元;
(2)解:由题意得:,
整理得:,
解得:,(不符合题意,舍去),
答:的值为200.
21.(1)购进购进袋鲜肉粽,袋蜜枣粽
(2)每袋鲜肉粽应降价4元
【分析】本题考查了二元一次方程组的应用以及一元二次方程的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)找准等量关系,正确列出一元二次方程.
(1)设购进x袋鲜肉粽,y袋蜜枣粽,根据题意列出可列出关于x,y的二元一次方程组,解之即可得出结论;
(2)设每袋鲜肉粽应降价元,此时每一袋的利润为:元,则降价当天的销售量为:件,降价之前鲜肉粽的销量为:根据题意得,解方程即可作答.
【详解】(1)解:设购进x袋鲜肉粽,y袋蜜枣粽,
根据题意得:,
解得:.
答:购进购进袋鲜肉粽,袋蜜枣粽;
(2)解:设每袋鲜肉粽应降价元,此时每一袋的利润为:元,
则降价当天的销售量为:件,
∴降价之前鲜肉粽的销量为:
根据题意得,
整理得:,
解得:(负值舍去).
答:每袋鲜肉粽应降价4元.
22.(1)
(2)80或100
【分析】本题考查了一次函数的应用以及一元二次方程的应用,解题的关键是:(1)根据各数量之间的关系,找出与之间的函数关系式;(2)找准等量关系,正确列出一元二次方程.
(1)根据“该商品每套的售价是50元时,每天可售出180套;若每套售价提高2元,则每天少卖4套.”列出解析式,即可求解;
(2)利用总利润每套的销售利润日销售量,可列出关于的一元二次方程,解之即可得出结论.
【详解】(1)解:由题意得,,
即:.
(2)由题知,
整理得到,
解得:,.
答:的值为80或100.
23.(1)甲、乙两商户每天分别生产小时和小时
(2)甲商户增加的生产时间为3小时
【分析】本题考查二元一次方程组的实际应用,一元二次方程的应用,正确的列出方程组和一元二次方程,是解题的关键:
(1)设甲、乙两商户每天分别生产小时和小时,根据甲乙两商户每天共生产16小时,且每天生产的三虾面总包数为11400包,列出方程组进行求解即可;
(2)设甲商户增加的生产时间为小时,根据两商户一天生产的面条总量将比原来多1200包,列出方程进行求解即可.
【详解】(1)解:设甲、乙两商户每天分别生产小时和小时,
则:,解得:;
答:甲、乙两商户每天分别生产小时和小时;
(2)设甲商户增加的生产时间为小时,则:乙商户增加的生产时间为小时,由题意,得:,
解得:或(不合题意,舍去);
答:甲商户增加的生产时间为3小时.
24.(1)桂花鱼的单价是14元,大罗非的单价是21元;
(2)m的值为2
【分析】本题考查了分式方程的应用以及一元二次方程的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)找准等量关系,正确列出一元二次方程.
(1)设桂花鱼的单价是x元,则大罗非的单价是元,利用数量=总价÷单价,结合用840元买的桂花鱼的数量比用同样价钱买大罗非的数量多20斤,可列出关于x的分式方程,解之经检验后,可得出桂花鱼的单价,再将其代入中,即可得出大罗非的单价;
(2)利用数量=总价÷单价,可求出第一次购买大罗非的数量,再利用总价=单价×数量,可列出关于m的一元二次方程,解之取其符合题意的值,即可得出结论.
【详解】(1)解:设桂花鱼的单价是x元,则大罗非的单价是元,
根据题意得: ,
解得:,
经检验,是所列方程的解,且符合题意,
∴(元).
答:桂花鱼的单价是14元,大罗非的单价是21元;
(2)第一次购买大罗非的数量是(斤).
根据题意得:,
整理得:,
解得:,(不符合题意,舍去).
答:m的值为2.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
人教版九年级上册数学第二十一章一元二次方程应用题训练
1.某工厂使用旧设备生产,每月生产收入是90万元,每月另需支付设备维护费5万元从今年1月份起使用新设备,生产收入提高且无设备维护费,使用当月生产收入达100万元,1至3月份累计收入达364万元,且2,3月份的生产收入保持相同的增长率,3月份后每月生产收入稳定在3月份的水平.
(1)求使用新设备后,2月3月生产收入的月增长率
(2)购进新设备需一次性支付640万元,则使用新设备几个月后,该厂所得累计利润不低于使用旧设备的累计利润?(累计利润是指累计生产收入减去旧设备维护费或新设备购进费)
2.我校新城校区新建一个三层停车楼,每一层布局如图所示.已知每层长为50米,宽20米.阴影部分设计为停车位,其余部分是等宽的通道,已知喷漆面积为736平方米.
(1)求通道的宽是多少米?
(2)据调查分析,停车场多余64个车位可以对外出租,当每个车位的月租金为200元时;当每个车位的月租金每上涨10元,就会少租出1个车位,既能优惠大众,又能使对外开放的月租金收入为14400元?
3.为防控“新冠”疫情,我巴南区启动新冠疫苗加强针接种工作.已知今年5月甲接种点平均每天接种加强针的人数比乙接种点平均每天接种加强针的人数多30%,两接种点平均每天共有460人接种加强针.
(1)求5月平均每天分别有多少人前往甲、乙两接种点接种加强针?
(2)6月份,甲接种点平均每天接种加强针的人数比5月少人,乙接种点平均每天接种加强针的人数比5月多20%,在天期间,甲、乙两接种点共有2250人接种加强针,求的值.
4.果农李明种植的草莓计划以每千克15元的单价对外批发销售,由于部分果农盲目扩大种植,造成该草莓滞销.李明为了加快销售,减少损失,对价格经过两次下调后,以每千克元的单价对外批发销售.
(1)求李明平均每次下调的百分率;
(2)小刘准备到李明处购买3吨该草莓,因数量多,李明决定再给予两种优惠方案以供其选择:方案一:打九折销售;方案二:不打折,每吨优惠现金400元.试问小刘选择哪种方案更优惠,请说明理由.
5.某农场要建一个长方形的养鸡场,鸡场的一边靠墙,(墙长)另外三边用木栏围成,木栏长.
(1)设平行于墙的一边长为x,垂直于墙的一边y,求y与x的函数关系式.
(2)若养鸡场面积为200平方米,求鸡场垂直于墙的一边长.
6.如图,某公园为方便游客观看鲜花,计划在一块长为60米,宽为40米的花圃四周修建同样宽度的通道,设通道宽为a米.
(1)用含a的式子表示通道和花圃的总面积;
(2)如果通道所占面积与花圃的面积相等,求出此时通道的宽度.
7.奥运会前夕,某超市在销售中发现:奥运会小饰品平均每天可售出200套,每件盈利20元.为了迎接奥运会,商场决定采取适当的降价措施,经市场调查发现:如果每套降价1元,那么平均每天就可多售出10套.
(1)当每套降价x元时,设每天销售数量为W,请直接写出W与x的函数关系式.
(2)要想平均每天在销售吉祥物上盈利3750元,那么每套应降价多少元?
8.如图,在一个边长为的正方形的四个角上分别剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),剩余的部分可以折成一个有盖的长方体盒子(纸板的厚度忽略不计),且折成的长方体盒子表面积是,设小正方形的边长为.
(1)请用x表示长方体的底面长和宽;
(2)长方体盒子的体积为多少?
9.如图,长方体的底面积为,长、宽、高的比为,则:
(1)这个长方体的长、宽、高分别是多少?
(2)长方体的表面积和体积分别是多少?
(3)若一只蚂蚁从顶点A沿长方体表面爬行到顶点B,直接写出从点A爬行到点B的最短路程是 .
10.某老牌造车企业为实现企业绿色低碳发展,通过技术改造升级,使新能源汽车项目的生产规模不断扩大,该企业9月,10月一共生产新能源汽车95000辆,其中10月份新能源汽车产量是9月份的倍少4000辆.(说明:生产的新能源汽车全部销售出去).
(1)求9月,10月新能源汽车产量各是多少辆
(2)若10月份每辆新能源汽车的利润为1万元,11月份新能源汽车产量比上月增加,11月份每辆新能源汽车的利润比上月增加,则11月份新能源汽车总利润达到66000万元,求m的值.
11.水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,这种水果每斤的售价每降低0.1元,每天可多售出20斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
12.近年来,电商平台直播带货成了一个火热的新兴职业,某主播带货图书《苏东坡传》,他用双语直播,风趣幽默,点燃了不同年龄者的读书热情.已知这本书的成本价为10元,规定销售单价不低于成本价,且不高于成本价的3倍,通过前几天的销售发现,该书每天的销售量y(本)与销售单价x(元/本)之间近似满足一次函数关系,部分对应数据如表:
x(元/本) … 15 25 …
y(本) … 600 400 …
(1)直接写出y关于x的函数关系式;
(2)若销售该书每天的利润为5000元,求该书的销售单价;
(3)销售该书每天的利润能否达到8000元?请说明理由.
13.振华商厦准备在月月销售一种多功能手机专用包,计划从厂家以每个元的价格进货,经过市场营销调查发现当每个手机专用包的售价为元时,月均销量为个,售价每增长元,月均销量就相应减少个.
(1)若使这种手机专用包的月均销量不低于个,每个手机专用包售价应不高于多少元?
(2)在()的条件下,当这种手机专用包销售单价为多少元时,月销售利润是元?
14.把一个足球垂直地面向上踢,t秒后该足球的高度h米适用公式,已知当足球踢出后4秒回到地面.
(1)求a的值.
(2)若该足球踢出t秒后和秒后,足球的高度相同,求t的值.
(3)是否有可能该足球踢出秒后的高度比踢出t秒后的高度高18米?通过计算说明.
15.某品牌纪念品每套成本为30元,当售价为40元时,平均每天的销售量为500套,经试销统计发现,如果该品牌纪念品售价每上涨1元,那么平均每天的销售量将减少10套,为了维护消费者利益,物价部门规定:该品牌纪念品售价不能超过进价的200%.设这种纪念品每套上涨x元.
(1)平均每天的销售量为______套(用含x的代数式表示):
(2)商家想要使这种纪念品的销售利润平均每天达到8000元,求每套纪念品应定价多少元?
16.士宝精品店以每件21元的价格购进一批商品,该商品可以自行定价,若每件商品售价为元,则可卖出件,但物价局限定每件商品的利润不得超过
(1)若商店计划要盈利400元,需要进货多少件?每件商品的售价应定为多少?
(2)在(1)的条件下,在实际销售的过程中,先将(1)中购进的商品卖出了部分后,决定将剩余商品打9折甩货,则至少先卖出多少件商品后再甩货才能保证利润不低于300元?
17.某商场销售一种学生用的计算器,进价为每台20元,售价为每台30元,每周可卖160台.根据市场调查,发现如果每台计算器的售价每上涨1元,每周就会少卖10台,但厂家规定最高每台售价不能超过33元.
(1)设每台售价上涨x元,每周的销售量为y台,则y与x之间的函数关系式为______;
(2)当计算器售价为多少元时,商场每周的利润恰好为1680元?(主要步骤列方程解答)
18.商场某种商品平均每天可销售件,每件盈利元.为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多售出2件,设每件商品降价x元,据此规律,请回答:
(1)商场日销售量增加______件,每件商品盈利(______)元;(用含x的代数式表示)
(2)在上述条件不变,销售正常情况下,每件商品降价多少元时,商场日盈利可达到元.
19.某商场经营一种成本为每千克40元的产品.
(1)已知四月份该产品的销售量为,经过适当调价后,6月份该产品的销量为,求月份该产品销售的月平均增长率.
(2)经市场调查发现,当该产品的售价为每千克50元时,月销售量为,每千克售价每涨价1元,月销售量将减少,该商场计划在月销售成本不超过10000元的情况下,要使月销售利润达到8000元,问销售该产品时每千克应涨多少元?
20.随着气温的逐步升高,空调成为了许多家庭的必需品,某商场最新推出的A、B两款空调凭借出色的性价比、智能互联功能以及时尚简约的设计风格,迅速赢得了年轻消费群体的青睐,已知A款空调的售价比B款空调的售价高600元,某商场在5月份销售了80台A款空调和100台B款空调,销售总金额为264000元.
(1)求A、B两款空调的销售单价分别为多少元?
(2)6月份的气温持续升高,商场抓住商机,对A款空调进行优惠促销,销售单价在5月份的基础上下降了m元,销售的数量比5月份增加了台,B款空调的销售单价不变,最终6月份两款空调一共销售了230台,销售金额比5月份增加了60000元.求m的值.
21.端午节吃粽子是中国人民的传统习俗.五月初利民副食店购进鲜肉粽、蜜枣粽两种粽子,其中鲜肉粽进价为15元/袋,售价为27元/袋,蜜枣粽进价为10元/袋,售价为19元/袋.利民副食店用660元购进鲜肉粽、蜜枣粽两种粽子共50袋.(注:利润=售价-进价)
(1)求购进鲜肉粽、蜜枣粽各多少袋?
(2)临近端午节,蜜枣粽售完,鲜肉粽还有剩余.副食店决定端午节当天对鲜肉粽降价销售,如果按原价销售,平均每天可售2袋.经调查发现,鲜肉粽每降价1元,平均每天可多售2袋.剩余的鲜肉粽在降价当天全部售完,50袋粽子共获利506元,每袋鲜肉粽应降价多少元?
22.第31届世界大学生夏季运动会在成都举办,其中大运会吉祥物蓉宝广受欢迎,成为热销商品.某商家以每套40元的价格购进一批蓉宝.当该商品每套的售价是50元时,每天可售出180套,若每套的售价每提高2元,则每天少卖4套.设蓉宝每套的售价定为x 元,该商品销售景y 套
(1)求y 与 x 之间的函数关系式;
(2)若每天销售所获的利润为4800元,求x的值.
23.“今天立夏,过来吃碗三虾面.”在百年老字号裕面堂内,一位老苏州说,苏州人立夏传统“尝三鲜”是蚕豆、苋菜、蒜苗,今年立夏提前吃碗夏令三虾面尝尝鲜.为了抓住这一商机,两商户决定生产预制面.据统计,甲商户每小时生产600包,乙商户每小时生产800包,甲乙两商户每天共生产16小时,且每天生产的三虾面总包数为11400包.
(1)甲、乙两商户每天分别生产多少小时?
(2)由于三虾面在网上直播热销,客户纷纷追加订单,两商户每天均增加了生产时间,其中甲商户比乙商户多增加2小时,在整个生产过程中,甲商户每小时产量不变,而乙商户由于机器损耗及人员不足,每增加一个小时,每小时产量将减少140包,这样两商户一天生产的面条总量将比原来多1200包.求:甲商户增加的生产时间为多少小时?
24.重庆市自发布“重庆市长江10年禁鱼通告”后,忠县内的黄钦水库自然生态养殖鱼在市场上热销,并被誉为“清凉五月天,黄钦自有贤”的美誉2024年五一假期依依同学旅游到此,并购买了若干桂花鱼和大罗非,她用840元买的桂花鱼的数量比用同样价钱买大罗非的数量多20斤,且大罗非的单价是桂花鱼的1.5倍,
(1)求桂花鱼、大罗非两种鱼的单价分别为多少元;
(2)两种鱼在得到一致好评后,依依决定再次购买这两种鱼作为“伴手礼”.由于商家对老顾客让利,其中桂花鱼按照原单价购买,大罗非的单价每斤降低m元,则购买的数量会比第一次购买大罗非的数量增加2m斤,第二次一共购买80斤鱼共用了1340元.求m的值.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.(1)每月的增长率是.
(2)使用新设备12个月后,该厂所得累计利润不低于使用旧设备的累计利润.
【分析】本题主要考查理一元二次方程的应用、一元一次不等式的应用等知识点,根据题意列出方程和不等式是解题的关键.
(1)设每月的增长率为x,那么2月份的生产收入为,三月份的生产收入为,根据1至3月份的生产收入累计可达364万元可列方程求解即可;
(2)设使用新设备y个月后,该厂所得累计利润不低于使用旧设备的累计利润,根据不等关系可列不等式求解即可.
【详解】(1)解:设每月的增长率为x,由题意得:,
解得或(不合题意舍去).
答:每月的增长率是.
(2)解:设使用新设备y个月后,该厂所得累计利润不低于使用旧设备的累计利润,依题意有,
解得.
答:使用新设备12个月后,该厂所得累计利润不低于使用旧设备的累计利润.
2.(1)通道的宽是2米
(2)每个车位的月租金应上涨40元
【分析】本题考查了一元二次方程的实际应用,解题的关键是设未知数,找出等量关系,正确列出方程.
(1)设通道的宽是x米,则每一层的停车位可合成长为米,宽为米的矩形,再根据喷漆面积列出方程求解即可;
(2)设每个车位的月租金上涨y元,则每个车位的月租金为元,少租出个车位,再根据月租金列出方程求解即可.
【详解】(1)解:设通道的宽是x米,则每一层的停车位可合成长为米,宽为米的长方形,
依题意得:,
整理得:,
解得:,(不符合题意,舍去).
答:通道的宽是2米.
(2)解:设每个车位的月租金上涨y元,则每个车位的月租金为元,少租出个车位,
依题意得:,
整理得:,
解得:,,
又∵要优惠大众,
.
答:每个车位的月租金应上涨40元.
3.(1)5月平均每天有260人前往甲接种点接种,200人前往乙接种点接种加强针
(2)的值为5
【分析】本题考查了一元一次方程的应用以及一元二次方程的应用,解题的关键是:找准等量关系,正确列出方程.
(1)设5月平均每天有人前往乙接种点接种加强针,则可以表示出前往甲接种点接种的人数,再根据两接种点的总人数列出方程即可;
(2)由5月份和6月份甲、乙两接种点的每天接种人数关系可以求出6月份的站点接种人数,再根据总的接种人数列出一元二次方程求解,此时解得的值有两个,再根据6月份甲接种点的人数判断值的取舍.
【详解】(1)解:设5月平均每天有人前往乙接种点接种加强针,则5月平均每天有人前往甲接种点接种,
由题意得:,
解得:,
∴人.
答:5月平均每天有260人前往甲接种点接种,200人前往乙接种点接种加强针;
(2)由题意得:6月平均每天有人前往甲接种点接种,有人前往乙接种点接种,
,
解得,
当时,,符合题意;
当时, ,不符合题意,舍去.
答:a的值为5.
4.(1)
(2)方案一,理由见解析
【分析】本题主要考查了一元二次方程的实际应用,有理数乘法的实际应用:
(1)设平均每次下调的百分率为x,根据经过两次下调后,以每千克元的单价对外批发销售列出方程求解即可;
(2)根据所给优惠方案分别求出两个方案的费用即可得到答案.
【详解】(1)解:设平均每次下调的百分率为x,
由题意,得,
解这个方程,得,
∵降价的百分率不可能大于1,
∴不符合题意,
符合题目要求的是,
答:平均每次下调的百分率是.
(2)解:小刘选择方案一购买更优惠,
理由:方案一所需费用为:(元),
方案二所需费用为:(元),
∵,
∴小刘选择方案一购买更优惠.
5.(1)
(2)
【分析】本题考查列一次函数解析式、一元二次方程的应用,(1)根据题意求解即可;
(2)根据长方形的面积公式列方程求解即可.
【详解】(1)解:由题意得,;
(2)解:由题意得,,
解得,
∴,
答:鸡场垂直于墙的一边长为.
6.(1)平方米
(2)10米
【分析】本题考查一元二次方程的实际应用:
(1)根据题意,得到总面积为长为,宽为的长方形的面积,列出代数式即可;
(2)根据题意,列出一元二次方程,进行求解即可.
【详解】(1)解:由题意,得,总面积为:平方米;
(2)由题意,得:,
解得:或(舍去);
∴通道的宽度为10米.
7.(1)
(2)每套应降价元
【分析】本题考查一元二次方程的运用,写出函数解析式,关键是看到降价和销售量的关系,然后根据利润可列方程求解.
(1)根据题干中降价和销售量的关系,写出函数解析式,即可解题;
(2)根据“平均每天在销售吉祥物上盈利3750元”列出方程求解,即可解题.
【详解】(1)解:根据题意可知;
(2)解:根据题意可知,
整理得,
解得,(舍去),
答:每套应降价元.
8.(1)长为,宽
(2)
【分析】本题考查了一元二次方程的应用、正方形与长方形面积的计算等知识,正确理解题意,找准数量关系列出一元二次方程是解题的关键.
(1)设剪去小正方形的边长为,则折成的长方体盒子的底面的长为,宽为;
(2)剩余的部分折成的长方体盒子的表面积是,列出一元二次方程,解方程即可.
【详解】(1)解:设剪去小正方形的边长为,
则折成的长方体盒子的底面的长为,宽为;
(2)解:由题意得:,
整理得:,
解得:或(不符合题意,舍去),
剪去小正方形的边长为,
长方体盒子的体积是,
则长方体盒子的体积为.
9.(1)这个长方体的长、宽、高分别是
(2)这个长方体的体积为,表面积为
(3)
【分析】本题考查了一元二次方程的实际应用,平面展开-最短路线问题,勾股定理应用.“化曲面为平面”是解决“怎样爬行最近”这类问题的关键.
(1)设这个长方体的长、宽、高分别是,根据长方体的底面积为,建立方程求解即可;
(2)由(1)中结果列式计算即可;
(3)把此长方体的一面展开,然后在平面内,利用勾股定理求点A和B点间的线段长,即可得到蚂蚁爬行的最短距离.应该是前面和上面展开,利用勾股定理可求得.
【详解】(1)解:设这个长方体的长、宽、高分别是,根据题意得:
,即,
(负值舍去)
这个长方体的长、宽、高分别是;
(2)解:由(1)知这个长方体的长、宽、高分别是,
这个长方体的体积为:,
这个长方体的表面积为:;
(3)解:平面展开图不唯一,故分情况分别计算,进行大、小比较,再从各个路线中确定最短的路线.
展开前面上面,由勾股定理得;
展开前面右面,由勾股定理得;
展开前面和左面,由勾股定理得.
,
最短路径的长为.
10.(1)9月新能源汽车的产量为45000辆,10月新能源汽车的产量为50000辆;
(2)m的值为20.
【分析】本题考查了一元一次方程的应用以及一元二次方程的应用,找准等量关系,正确列出方程是解题的关键.
(1)设9月新能源汽车的产量为x辆,则10月新能源汽车的产量为辆,根据该厂9,10月共生产新能源汽车95000辆,即可得出关于x的一元一次方程,解之即可求出x的值,再将其代入中即可求出10月新能源汽车的产量;
(2)利用月利润=每辆的利润×月产量,即可得出关于m的一元二次方程,解之取其正值即可得出结论.
【详解】(1)解:设9月新能源汽车的产量为x辆,则10月新能源汽车的产量为辆,
依题意得:,
解得:,
∴.
答:9月新能源汽车的产量为45000辆,10月新能源汽车的产量为50000辆;
(2)解:依题意得:,
整理得:,
解得:,(不合题意,舍去).
答:m的值为20.
11.(1)
(2)张阿姨需将每斤的售价降低1元或0.5元
【分析】本题考查理解题意的能力,第一问关键求出每千克的利润,求出总销售量,从而利润.第二问,根据售价和销售量的关系,以利润作为等量关系列方程求解.
(1)销售量原来销售量下降销售量,据此列式即可;
(2)根据销售量每斤利润总利润列出方程求解即可.
【详解】(1)将这种水果每斤的售价降低元,则每天的销售量是(斤,
故答案为:;
(2)根据题意得:,
解得:或,
答:张阿姨需将每斤的售价降低1元或0.5元.
12.(1)
(2)20元
(3)销售该书每天的利润不能达到8000元,理由见解析
【分析】本题考查一次函数的实际应用,一元二次方程的实际应用.掌握利用待定系数法求一次函数解析式和理解题意,找出等量关系,列出方程是解题关键.
(1)设y关于x的函数关系式为,再利用待定系数法求解即可;
(2)根据题意可列出关于x的一元二次方程,求解,再舍去不合题意的解即可;
(3)根据题意可列出关于x的一元二次方程,根据其根的判别式小于0,可判断其无解,即说明销售该书每天的利润不能达到8000元.
【详解】(1)解:设y关于x的函数关系式为,
根据题意得:,
解得:.
∵规定销售单价不低于成本价,且不高于成本价的3倍,
∴,
∴y关于x的函数关系式为;
(2)解:根据题意得:,即,,
整理得:,
解得:,(舍),
答:该书的销售单价为20元;
(3)解:根据题意得:,即,,
整理得:,
∵,
∴原方程无解,
∴销售该书每天的利润不能达到8000元.
13.(1)每个手机专用包售价应不高于元;
(2)当该这种手机专用包销售单价为元时,销售利润是元.
【分析】()设每个手机专用包售价为元,根据题意列出,然后求解即可;
()由题意列方程,然后解方程检验即可;
本题主要考查了一元二次方程的应用,一元一次不等式的应用,明确题意,准确得到数量关系是解题的关键.
【详解】(1)设每个手机专用包售价为元,
依题意得:
解得:,
∴的最大值为,
∴每个手机专用包售价应不高于元;
(2)依题意得:
整理得:,
解得:,(不符合题意,舍去),
∴当该这种手机专用包销售单价为元时,销售利润是元.
14.(1)20
(2)
(3)没有可能,计算见解析
【分析】本题考查了一元二次方程的应用,熟练掌握知识点,正确理解题意是解题的关键.
(1)取,代入公式可得的值;
(2)由踢出t秒后和秒后,足球的高度相同得,解方程即可;
(3)求得自变量为和时的函数值,相减为18,看求得的是否符合题意即可.
【详解】(1)解:由题意得:当时,.
.
解得:;
(2)解:由(1)得:,
∵踢出t秒后和秒后,足球的高度相同
∴,
解得:;
(3)解:由题意得:.
.
解得:(不合题意,舍去).
没有可能该足球踢出秒后的高度比踢出秒后的高度高18米.
15.(1)
(2)每套纪念品应定价50元.
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
(1)由题意即可得出结论;
(2)设这种纪念品每套上涨元,则每套纪念品应定价为元,平均每天的销售量为套,根据这种纪念品的销售利润平均每天达到8000元,列出一元二次方程,解之取符合题意的值即可.
【详解】(1)解:由题意可知,平均每天的销售量为套,
故答案为:;
(2)解:设这种纪念品每套上涨元,则每套纪念品应定价为元,平均每天的销售量为套,
由题意得:,
整理得:,
解得:,(不符合题意,舍去),
,
答:每套纪念品应定价50元.
16.(1)需要进货100件,每件商品应定价25元
(2)至少先卖出60件商品后再甩货才能保证利润不低于300元
【分析】本题考查了一元二次方程的应用及一元一次不等式的应用,熟练掌握利润的计算方法是解题的关键.
(1)利润=售价-进价,总利润=单件利润×总件数,注意限制条件的作用.
(2)设先卖出m件商品后再甩货才能保证利润不低于300元,根据题意列出不等式解决即可.
【详解】(1)解:依题意,
整理得,
解得,.
因为,
所以不合题意,舍去.
所以(件).
答:需要进货100件,每件商品应定价25元.
(2)设先卖出m件商品后再甩货才能保证利润不低于300元,由题意得:
,
解得:,
至少先卖出60件商品后再甩货才能保证利润不低于300元.
17.(1)
(2)当计算器定价为32元时,商场每周的利润恰好为1680元.
【分析】本题考查的是一次函数的实际应用,一元二次方程的实际应用,理解题意是解本题的关键;
(1)由实际销售量等于原来销量减去减少的销量即可得到关系式;
(2)由每件计算器的利润乘以销售数量建立方程求解即可;
【详解】(1)解:由题意可得:;
(2)解:由题意可得:,
∴,
解得,,,
∵,
∴符合题意,
∴此时计算器的售价为(元),
即当计算器定价为32元时,商场每周的利润恰好为1680元.
18.(1),
(2)元
【分析】本题考查了列代数式,一元二次方程的应用.熟练掌握列代数式,一元二次方程的应用是解题的关键.
(1)由题意知,每件商品降价x元,商场日销售量增加件,每件商品盈利元;
(2)依题意得,,整理得,,计算求出满足要求的解即可.
【详解】(1)解:由题意知,每件商品降价x元,商场日销售量增加件,每件商品盈利元,
故答案为:,;
(2)解:依题意得,,整理得,,
,
解得,或,
∵为了尽快减少库存,
∴,
∴每件商品降价元时,商场日盈利可达到元.
19.(1)月份该产品销售的月平均增长率为
(2)销售该产品时每千克应涨30元
【分析】此题考查的是一元二次方程的应用,读懂题意,找到合适的等量关系,然后设出未知数正确列出方程是解题的关键.
(1)设月份该产品销售的月平均增长率为x,列方程并解方程即可解决;
(2)根据销售单价每涨价1元,月销售量就减少10千克,结合月销售利润=每件利润×数量即可列出方程,解方程即可;
【详解】(1)解:设月份该产品销售的月平均增长率为x,由题意得:
,
解得:(不合题意舍去),
答:月份该产品销售的月平均增长率为;
(2)解:设销售该产品时每千克应涨y元,
,
解得:,
当时,月销售成本为,不合题意舍去,
当时,月销售成本为,符合题意,
∴,
答:销售该产品时每千克应涨30元.
20.(1)款空调的销售单价为1800元,款空调的销售单价为1200元
(2)的值为200
【分析】本题考查了一元二次方程的应用以及二元一次方程组的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)找准等量关系,正确列出一元二次方程.
(1)设款空调的销售单价为元,款空调的销售单价为元,根据款空调的售价比款空调的售价高600元,某商场在5月份销售了80台款空调和100台款空调,销售总金额为264000元.列出二元一次方程组,解方程组即可;
(2)根据最终6月份两款空调一共销售了230台,销售金额比5月份增加了60000元.列出一元二次方程,解之取符合题意的值即可.
【详解】(1)解:设款空调的销售单价为元,款空调的销售单价为元,
由题意得:,
解得:,
答:款空调的销售单价为1800元,款空调的销售单价为1200元;
(2)解:由题意得:,
整理得:,
解得:,(不符合题意,舍去),
答:的值为200.
21.(1)购进购进袋鲜肉粽,袋蜜枣粽
(2)每袋鲜肉粽应降价4元
【分析】本题考查了二元一次方程组的应用以及一元二次方程的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)找准等量关系,正确列出一元二次方程.
(1)设购进x袋鲜肉粽,y袋蜜枣粽,根据题意列出可列出关于x,y的二元一次方程组,解之即可得出结论;
(2)设每袋鲜肉粽应降价元,此时每一袋的利润为:元,则降价当天的销售量为:件,降价之前鲜肉粽的销量为:根据题意得,解方程即可作答.
【详解】(1)解:设购进x袋鲜肉粽,y袋蜜枣粽,
根据题意得:,
解得:.
答:购进购进袋鲜肉粽,袋蜜枣粽;
(2)解:设每袋鲜肉粽应降价元,此时每一袋的利润为:元,
则降价当天的销售量为:件,
∴降价之前鲜肉粽的销量为:
根据题意得,
整理得:,
解得:(负值舍去).
答:每袋鲜肉粽应降价4元.
22.(1)
(2)80或100
【分析】本题考查了一次函数的应用以及一元二次方程的应用,解题的关键是:(1)根据各数量之间的关系,找出与之间的函数关系式;(2)找准等量关系,正确列出一元二次方程.
(1)根据“该商品每套的售价是50元时,每天可售出180套;若每套售价提高2元,则每天少卖4套.”列出解析式,即可求解;
(2)利用总利润每套的销售利润日销售量,可列出关于的一元二次方程,解之即可得出结论.
【详解】(1)解:由题意得,,
即:.
(2)由题知,
整理得到,
解得:,.
答:的值为80或100.
23.(1)甲、乙两商户每天分别生产小时和小时
(2)甲商户增加的生产时间为3小时
【分析】本题考查二元一次方程组的实际应用,一元二次方程的应用,正确的列出方程组和一元二次方程,是解题的关键:
(1)设甲、乙两商户每天分别生产小时和小时,根据甲乙两商户每天共生产16小时,且每天生产的三虾面总包数为11400包,列出方程组进行求解即可;
(2)设甲商户增加的生产时间为小时,根据两商户一天生产的面条总量将比原来多1200包,列出方程进行求解即可.
【详解】(1)解:设甲、乙两商户每天分别生产小时和小时,
则:,解得:;
答:甲、乙两商户每天分别生产小时和小时;
(2)设甲商户增加的生产时间为小时,则:乙商户增加的生产时间为小时,由题意,得:,
解得:或(不合题意,舍去);
答:甲商户增加的生产时间为3小时.
24.(1)桂花鱼的单价是14元,大罗非的单价是21元;
(2)m的值为2
【分析】本题考查了分式方程的应用以及一元二次方程的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)找准等量关系,正确列出一元二次方程.
(1)设桂花鱼的单价是x元,则大罗非的单价是元,利用数量=总价÷单价,结合用840元买的桂花鱼的数量比用同样价钱买大罗非的数量多20斤,可列出关于x的分式方程,解之经检验后,可得出桂花鱼的单价,再将其代入中,即可得出大罗非的单价;
(2)利用数量=总价÷单价,可求出第一次购买大罗非的数量,再利用总价=单价×数量,可列出关于m的一元二次方程,解之取其符合题意的值,即可得出结论.
【详解】(1)解:设桂花鱼的单价是x元,则大罗非的单价是元,
根据题意得: ,
解得:,
经检验,是所列方程的解,且符合题意,
∴(元).
答:桂花鱼的单价是14元,大罗非的单价是21元;
(2)第一次购买大罗非的数量是(斤).
根据题意得:,
整理得:,
解得:,(不符合题意,舍去).
答:m的值为2.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
