小升初模拟卷(试题)-六年级下册数学北师大版(含答案)
文档属性
| 名称 | 小升初模拟卷(试题)-六年级下册数学北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 69.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-10 12:17:36 | ||
图片预览



文档简介
小升初模拟卷(试题)
一、填空题。(共10题,每空1分,共17分)
1.2024年“五一”假期,全国国内旅游出游二亿七千四百万人次,横线上的数写作 人次;实现国内旅游收入148056000000元,省略亿后面的尾数是 亿元。
2. ÷10= =0.4= %
3.若用(5、2)表示第5列第2行的位置.那么(9,12)表示第 列第 行的位置。
4.在一座长800 m的大桥两边挂彩灯,起点和终点都挂,一共挂了202盏。若相邻两盏彩灯之间的距离相等,则相邻两盏彩灯之间的距离是 m。
5.花店购进一批鲜花,每10朵扎成一束或每14朵扎成一束都正好余下3朵,这批鲜花至少有 朵。
6.从一个长5分米,宽4分米的长方形木板上锯下一个最大的圆,圆的周长是 分米,剩下的面积是 平方分米.
7.一个圆柱体,已知高每增加1厘米,它的侧面就增加31.4平方厘米,如果高是16厘米,它的体积是 立方厘米。
8.一个旅游团队共有65人,在宾馆租住了双人间和三人间共25间,算一算,双人间住了 间,三人间住了 间。
9.等底等高的圆柱和圆锥的体积和是24立方米,这个圆柱的体积是 立方米,圆锥的体积是 立方米。
10.在比例尺是1:20000的地图上,量得甲、乙两地相距5厘米,甲、乙两地的实际距离是 千米。
二、选择题。(共6题,每小题1分,共6分)
11.低于正常水位0.16米记为-0.16米,高于正常水位0.02米记作( )米。
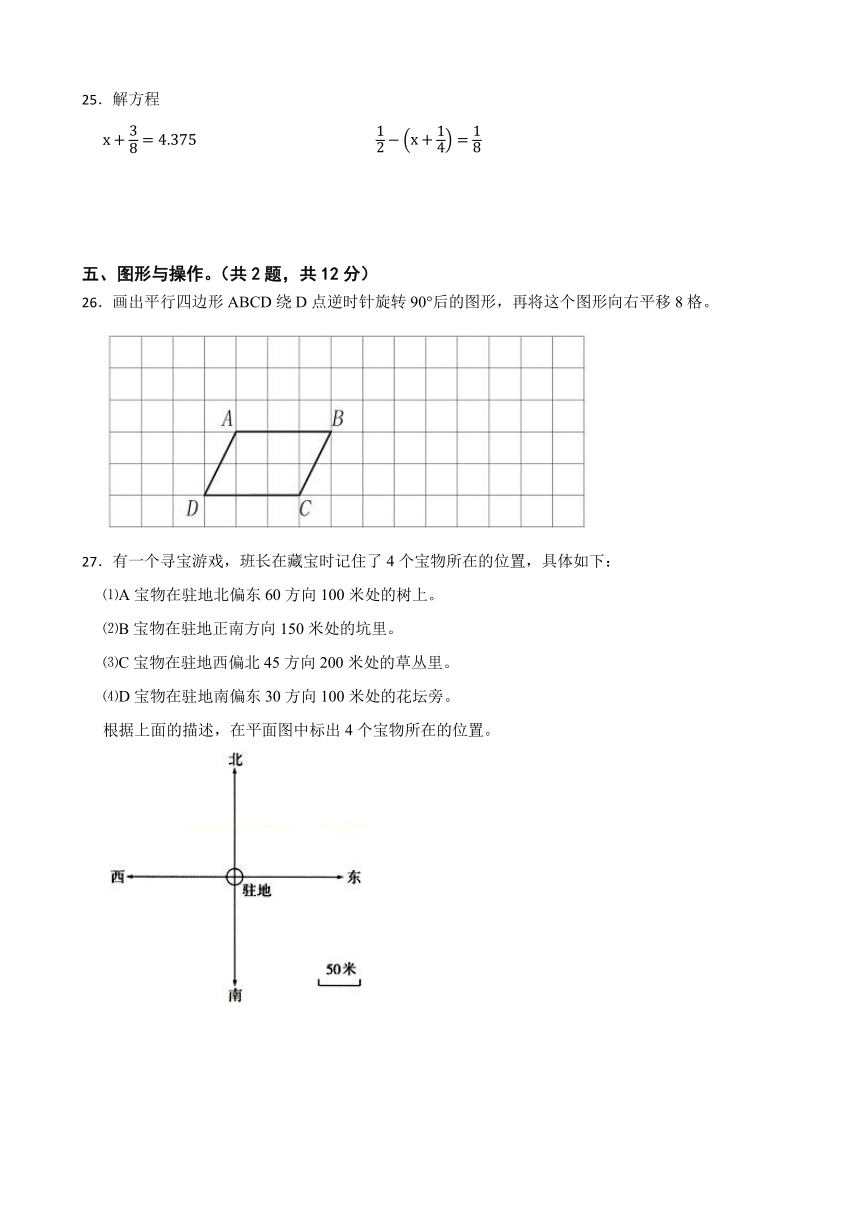
A.+0.02 B.-0.02 C.+0.18 D.-0.14
12.德国数学家哥德巴赫提出猜想:所有大于2的偶数,都可以表示为两个质数的和。该猜想成为数学中一个著名的难题,被称为“数学皇冠上的明珠”。下面符合这个猜想的是( )
A.20=2+18 B.15=2+13 C.18=3+15 D.12=5+7
13.要想清楚地反映某地区近年来经济发展变化情况,用( )统计图更合适。
A.条形 B.折线 C.扇形 D.复式
14.下图是一个长方体的展开图(单位:cm),这个长方体的体积是( )cm3。
A.180 B.216 C.288 D.864
15.如果一个三角形的三个内角度数之比为5:4:9,那么这个三角形是( )。
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
16.今年“五一”假期,某景区的门票收入比去年同期的门票收入增加三成五,去年“五一”假期的门票收入是270万元,求今年“五一”假期的门票收入是多少万元。下面列式正确的是( )。
A.270×35% B.270×(1+35%)
C.270÷35% D.270÷(1+35%)
三、判断题。(共6题,每题1分,共6分)
17. 4.698保留两位小数是4.70,可以写成4.7。( )
18.质数和质数的乘积还是质数。( )
19.假分数的分子一定比分母小.( )
20.钝角三角形中两个锐角的和一定小于 90°。( )
21.两个面积相等的梯形一定能拼出一个平行四边形。( )
22.圆柱的体积等于圆锥体积的3倍。( )
四、计算题。(共3题,共33分)
23.直接写得数。
+ = 469-197= = 12.5×= 23×498≈
3.48+6.52= 21÷ = 0.65÷1.3= 60÷6%= 632÷69≈
24.计算下面各题,能简算的要简算。
①1254﹣267﹣333 ②63×65+63×135
③900÷25÷4 ④1.28+1.1+0.72+8.9
25.解方程
五、图形与操作。(共2题,共12分)
26.画出平行四边形ABCD绕D点逆时针旋转90°后的图形,再将这个图形向右平移8格。
27.有一个寻宝游戏,班长在藏宝时记住了4个宝物所在的位置,具体如下:
⑴A宝物在驻地北偏东60方向100米处的树上。
⑵B宝物在驻地正南方向150米处的坑里。
⑶C宝物在驻地西偏北45方向200米处的草丛里。
⑷D宝物在驻地南偏东30方向100米处的花坛旁。
根据上面的描述,在平面图中标出4个宝物所在的位置。
六、解决问题。(共5题,共26分)
28.王奶奶把8000元存入银行,存期为三年定期,年利率为2.75%。到期时,王奶奶一共能取出多少钱
29.一个圆锥形小麦堆,底面直径为6米,高1.5米。如果每立方米小麦重0.75吨,这堆小麦约重多少吨?(得数保留一位小数)
30.有一些相同的房间需要粉刷,一天3名师傅去粉刷7个房间,结果其中有30m2墙面未来得及粉刷:同样的时间内5名徒弟粉刷了9个房间之外,还多粉刷了另外的10m墙面.每名师傅比徒弟一天多刷20m墙面.求每个房间需要粉刷的墙面面积。
31.佳运公司为了节约能源,使用新能源汽车代替燃油汽车。一辆新能源汽车每行驶300千米可节约燃油1.5升。照这样计算,这辆能源汽车每行驶300千米可节约燃油1.5升。照这样计算,这辆汽车每年大约要行驶28000千米,每年大约可节约燃油多少升?(用比例知识解答)
32.甲乙两种商品的原价之比是7:4,如果它们的价格分别上涨35元,那么价格之比变为8:5,则甲乙两种商品的原价分别是多少
参考答案
1.274000000;1481
2.4;2;40
3.9;12
4.8
5.73
6.12.56;7.44
7.1256
8.10;15
9.18;6
10.1
11.A
12.D
13.B
14.A
15.B
16.B
17.错误
18.错误
19.错误
20.正确
21.错误
22.错误
23.+=0.55;469-197=272;÷=;12.5×=10;23×498≈10000;
3.48+6.52=10;21÷=49;0.65÷1.3=0.5;60÷6%=1000;632÷69≈9。
24.解:①1254﹣267﹣333
=1254﹣(267+333)
=1254﹣600
=654
②63×65+63×135
=(65+135)×63
=200×63
=12600
③900÷25÷4
=900÷(25×4)
=900÷100
=9
④1.28+1.1+0.72+8.9
=(1.28+0.72)+(1.1+8.9)
=2+2
=4
25.
解: x=4.375-0.375
x=4 解: x+=-
x+=
x=-
26.
27.解:如图:
28.解:8000+8000×2.75%×3
=8000+220×3
=8000+660
=8660(元)
答:王奶奶一共能取出8660元。
29.解:×3.14×(6÷2)2×1.5×0.75
=×3.14×9×1.5×0.75
=3×3.14×1.5×0.75
=14.13×0.75
≈10.6(吨)
答:这堆小麦约重10.6吨。
30.解:设每个房间需要粉刷的墙面面积为xm2 则每名师傅每天粉刷墙壁,每名徒弟每天粉刷墙壁,则
35x-150-27x-30=300
8x-180=300
8x=480
x=60
答:每个房间需要粉刷的墙面面积为 。
31.解:设每年大约可节约燃油 x升。
1.5:300= x:28000
300 x =1.5×28000
300 x =42000
x=42000÷300
x=140
答:每年大约可节约燃油140升。
32.解:设甲原价为7x元,则乙原价为4x元。
(7x+35):(4x+35)=8:5
5×(7x+35)=8×(4x+35)
35x+175=32x+280
35x-32x=280-175
3x=105
x=35
甲:7x=35×7=245
乙:4x=35×4=140。
答:甲原价是245元,乙原价是140元。
一、填空题。(共10题,每空1分,共17分)
1.2024年“五一”假期,全国国内旅游出游二亿七千四百万人次,横线上的数写作 人次;实现国内旅游收入148056000000元,省略亿后面的尾数是 亿元。
2. ÷10= =0.4= %
3.若用(5、2)表示第5列第2行的位置.那么(9,12)表示第 列第 行的位置。
4.在一座长800 m的大桥两边挂彩灯,起点和终点都挂,一共挂了202盏。若相邻两盏彩灯之间的距离相等,则相邻两盏彩灯之间的距离是 m。
5.花店购进一批鲜花,每10朵扎成一束或每14朵扎成一束都正好余下3朵,这批鲜花至少有 朵。
6.从一个长5分米,宽4分米的长方形木板上锯下一个最大的圆,圆的周长是 分米,剩下的面积是 平方分米.
7.一个圆柱体,已知高每增加1厘米,它的侧面就增加31.4平方厘米,如果高是16厘米,它的体积是 立方厘米。
8.一个旅游团队共有65人,在宾馆租住了双人间和三人间共25间,算一算,双人间住了 间,三人间住了 间。
9.等底等高的圆柱和圆锥的体积和是24立方米,这个圆柱的体积是 立方米,圆锥的体积是 立方米。
10.在比例尺是1:20000的地图上,量得甲、乙两地相距5厘米,甲、乙两地的实际距离是 千米。
二、选择题。(共6题,每小题1分,共6分)
11.低于正常水位0.16米记为-0.16米,高于正常水位0.02米记作( )米。
A.+0.02 B.-0.02 C.+0.18 D.-0.14
12.德国数学家哥德巴赫提出猜想:所有大于2的偶数,都可以表示为两个质数的和。该猜想成为数学中一个著名的难题,被称为“数学皇冠上的明珠”。下面符合这个猜想的是( )
A.20=2+18 B.15=2+13 C.18=3+15 D.12=5+7
13.要想清楚地反映某地区近年来经济发展变化情况,用( )统计图更合适。
A.条形 B.折线 C.扇形 D.复式
14.下图是一个长方体的展开图(单位:cm),这个长方体的体积是( )cm3。
A.180 B.216 C.288 D.864
15.如果一个三角形的三个内角度数之比为5:4:9,那么这个三角形是( )。
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
16.今年“五一”假期,某景区的门票收入比去年同期的门票收入增加三成五,去年“五一”假期的门票收入是270万元,求今年“五一”假期的门票收入是多少万元。下面列式正确的是( )。
A.270×35% B.270×(1+35%)
C.270÷35% D.270÷(1+35%)
三、判断题。(共6题,每题1分,共6分)
17. 4.698保留两位小数是4.70,可以写成4.7。( )
18.质数和质数的乘积还是质数。( )
19.假分数的分子一定比分母小.( )
20.钝角三角形中两个锐角的和一定小于 90°。( )
21.两个面积相等的梯形一定能拼出一个平行四边形。( )
22.圆柱的体积等于圆锥体积的3倍。( )
四、计算题。(共3题,共33分)
23.直接写得数。
+ = 469-197= = 12.5×= 23×498≈
3.48+6.52= 21÷ = 0.65÷1.3= 60÷6%= 632÷69≈
24.计算下面各题,能简算的要简算。
①1254﹣267﹣333 ②63×65+63×135
③900÷25÷4 ④1.28+1.1+0.72+8.9
25.解方程
五、图形与操作。(共2题,共12分)
26.画出平行四边形ABCD绕D点逆时针旋转90°后的图形,再将这个图形向右平移8格。
27.有一个寻宝游戏,班长在藏宝时记住了4个宝物所在的位置,具体如下:
⑴A宝物在驻地北偏东60方向100米处的树上。
⑵B宝物在驻地正南方向150米处的坑里。
⑶C宝物在驻地西偏北45方向200米处的草丛里。
⑷D宝物在驻地南偏东30方向100米处的花坛旁。
根据上面的描述,在平面图中标出4个宝物所在的位置。
六、解决问题。(共5题,共26分)
28.王奶奶把8000元存入银行,存期为三年定期,年利率为2.75%。到期时,王奶奶一共能取出多少钱
29.一个圆锥形小麦堆,底面直径为6米,高1.5米。如果每立方米小麦重0.75吨,这堆小麦约重多少吨?(得数保留一位小数)
30.有一些相同的房间需要粉刷,一天3名师傅去粉刷7个房间,结果其中有30m2墙面未来得及粉刷:同样的时间内5名徒弟粉刷了9个房间之外,还多粉刷了另外的10m墙面.每名师傅比徒弟一天多刷20m墙面.求每个房间需要粉刷的墙面面积。
31.佳运公司为了节约能源,使用新能源汽车代替燃油汽车。一辆新能源汽车每行驶300千米可节约燃油1.5升。照这样计算,这辆能源汽车每行驶300千米可节约燃油1.5升。照这样计算,这辆汽车每年大约要行驶28000千米,每年大约可节约燃油多少升?(用比例知识解答)
32.甲乙两种商品的原价之比是7:4,如果它们的价格分别上涨35元,那么价格之比变为8:5,则甲乙两种商品的原价分别是多少
参考答案
1.274000000;1481
2.4;2;40
3.9;12
4.8
5.73
6.12.56;7.44
7.1256
8.10;15
9.18;6
10.1
11.A
12.D
13.B
14.A
15.B
16.B
17.错误
18.错误
19.错误
20.正确
21.错误
22.错误
23.+=0.55;469-197=272;÷=;12.5×=10;23×498≈10000;
3.48+6.52=10;21÷=49;0.65÷1.3=0.5;60÷6%=1000;632÷69≈9。
24.解:①1254﹣267﹣333
=1254﹣(267+333)
=1254﹣600
=654
②63×65+63×135
=(65+135)×63
=200×63
=12600
③900÷25÷4
=900÷(25×4)
=900÷100
=9
④1.28+1.1+0.72+8.9
=(1.28+0.72)+(1.1+8.9)
=2+2
=4
25.
解: x=4.375-0.375
x=4 解: x+=-
x+=
x=-
26.
27.解:如图:
28.解:8000+8000×2.75%×3
=8000+220×3
=8000+660
=8660(元)
答:王奶奶一共能取出8660元。
29.解:×3.14×(6÷2)2×1.5×0.75
=×3.14×9×1.5×0.75
=3×3.14×1.5×0.75
=14.13×0.75
≈10.6(吨)
答:这堆小麦约重10.6吨。
30.解:设每个房间需要粉刷的墙面面积为xm2 则每名师傅每天粉刷墙壁,每名徒弟每天粉刷墙壁,则
35x-150-27x-30=300
8x-180=300
8x=480
x=60
答:每个房间需要粉刷的墙面面积为 。
31.解:设每年大约可节约燃油 x升。
1.5:300= x:28000
300 x =1.5×28000
300 x =42000
x=42000÷300
x=140
答:每年大约可节约燃油140升。
32.解:设甲原价为7x元,则乙原价为4x元。
(7x+35):(4x+35)=8:5
5×(7x+35)=8×(4x+35)
35x+175=32x+280
35x-32x=280-175
3x=105
x=35
甲:7x=35×7=245
乙:4x=35×4=140。
答:甲原价是245元,乙原价是140元。
同课章节目录
