第二十二章二次函数 章节检测 (无答案)2024-2025学年人教版数学九年级上册
文档属性
| 名称 | 第二十二章二次函数 章节检测 (无答案)2024-2025学年人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 286.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-10 17:16:54 | ||
图片预览

文档简介
第二十二章二次函数 章节检测 2024-2025学年人教版数学九年级上册
一、单选题
1.二次函数y=﹣(x+3)2+2图象的开口方向、对称轴和顶点坐标分别为( )
A.向下,x=3,(3,2) B.向下,x=﹣3,(3,2)
C.向上,x=﹣3,(3,2) D.向下,x=﹣3,(﹣3,2)
2.在同一平面直角坐标系中,一次函数与的图像可能是( )
A. B.
C. D.
3.已知二次函数y=﹣x2﹣2bx+c,当x<2时,y的值随x的增大而增大,则实数b的取值范围是( )
A.b≥﹣1 B.b≤﹣1 C.b≥﹣2 D.b≤﹣2
4.下列二次函数的图象与x轴没有交点的是( )
A.y=-3x2+2x B.y=x2-3x-4
C.y=x2-4x+4 D.y=x2+4x+5
5.如图,抛物线的顶点在的边所在的直线上运动,的顶点的坐标为,点的坐标为,若抛物线与的边、都有公共点,则的取值范围是( )
A. B. C. D.
6.二次函数y=-3x2-6x+5的图像的顶点坐标是( )
A.(-1,8) B.(1,8) C.(-1,2) D.(1,-4)
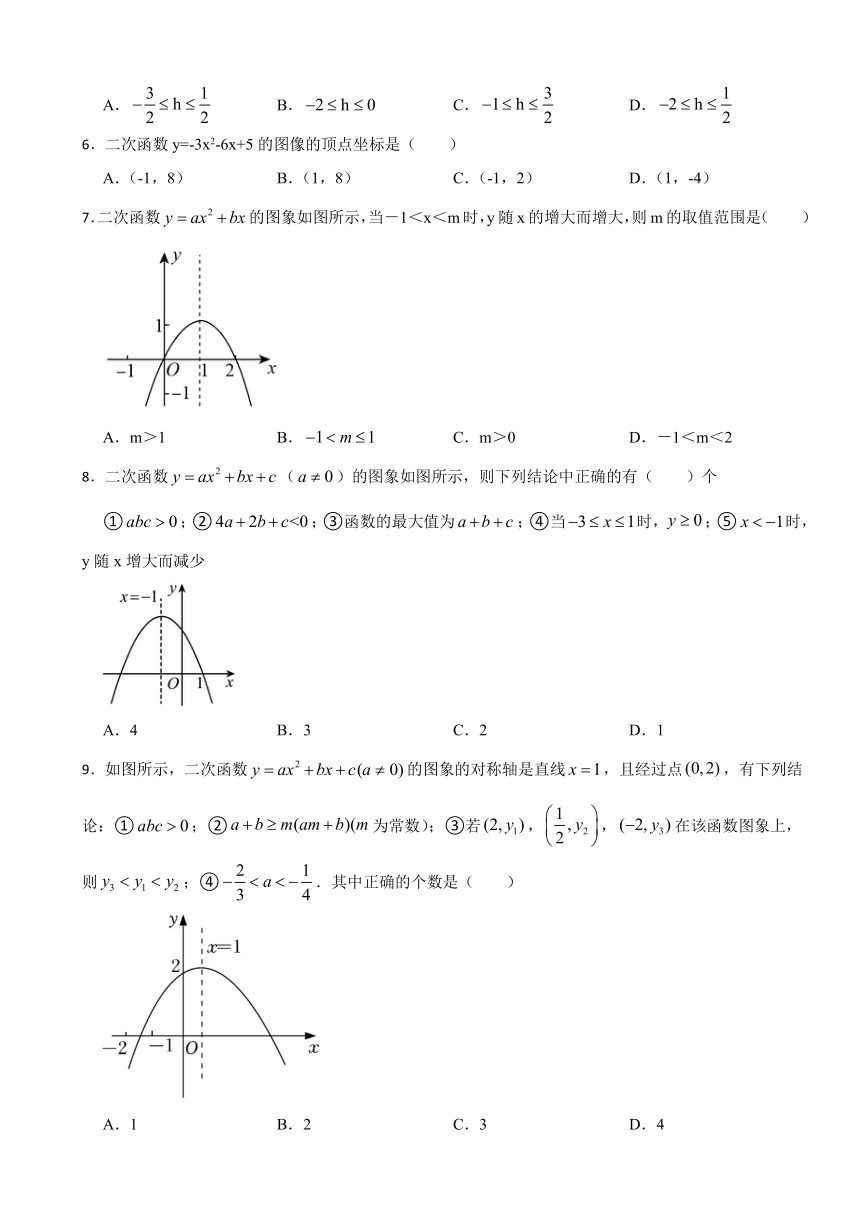
7.二次函数的图象如图所示,当-1<x<m时,y随x的增大而增大,则m的取值范围是( )
A.m>1 B. C.m>0 D.-1<m<2
8.二次函数()的图象如图所示,则下列结论中正确的有( )个
①;②;③函数的最大值为;④当时,;⑤时,y随x增大而减少
A.4 B.3 C.2 D.1
9.如图所示,二次函数的图象的对称轴是直线,且经过点,有下列结论:①;②为常数);③若,,在该函数图象上,则;④.其中正确的个数是( )
A.1 B.2 C.3 D.4
10.如图,在平面直角坐标系中,抛物线y=ax2+bx+3(a<0)交x轴于A,B两点(B在A左侧),交y轴于点C,且CO=AO,分别以BC,AC为边向外作正方形BCDE、正方形ACGH,记它们的面积分别为S1,S2,△ABC面积记为S3,当S1+S2=6S3时,b的值为( )
A. B. C. D.
二、填空题
11.抛物线 的对称轴为 。
12.点 是二次函数 图象上一点,则-3m2+6m的值为 .
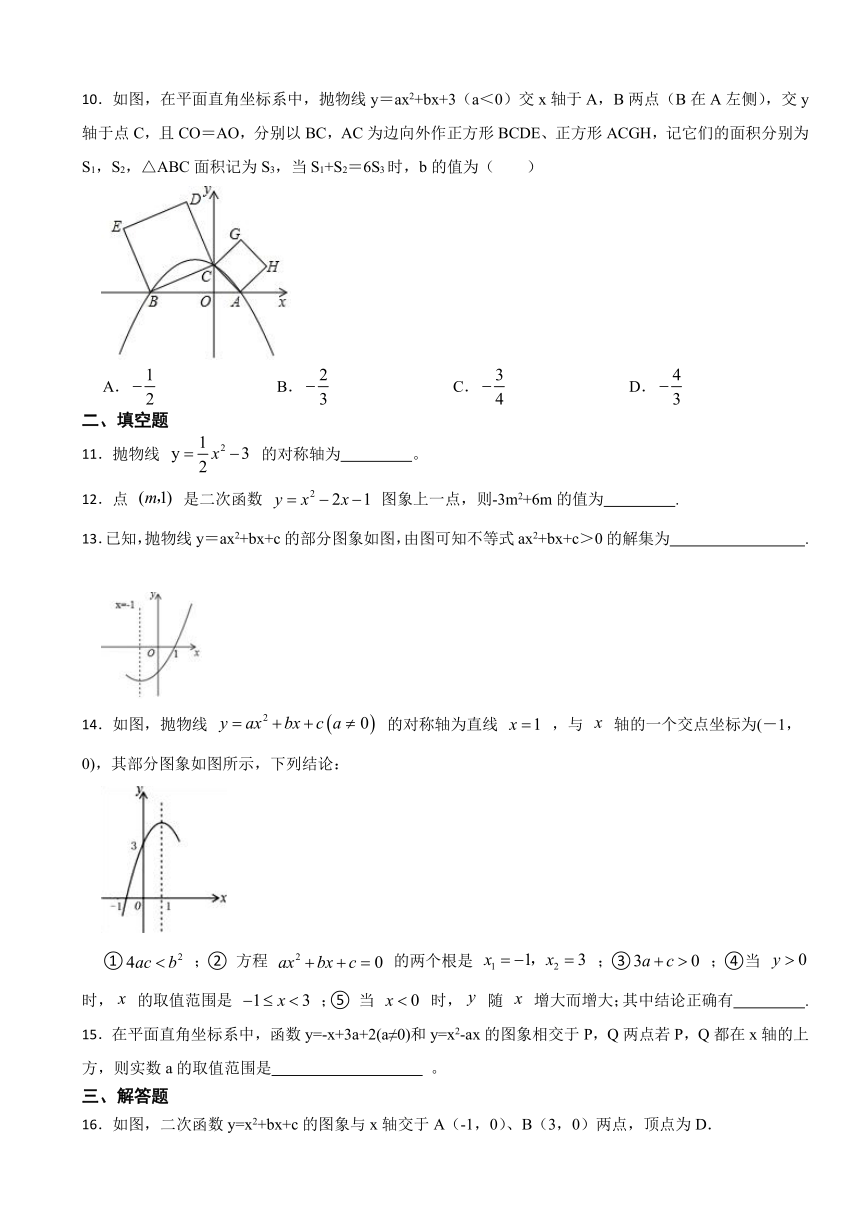
13.已知,抛物线y=ax2+bx+c的部分图象如图,由图可知不等式ax2+bx+c>0的解集为 .
14.如图,抛物线 的对称轴为直线 ,与 轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
① ;② 方程 的两个根是 ;③ ;④当 时, 的取值范围是 ;⑤ 当 时, 随 增大而增大;其中结论正确有 .
15.在平面直角坐标系中,函数y=-x+3a+2(a≠0)和y=x2-ax的图象相交于P,Q两点若P,Q都在x轴的上方,则实数a的取值范围是 。
三、解答题
16.如图,二次函数y=x2+bx+c的图象与x轴交于A(-1,0)、B(3,0)两点,顶点为D.
(1)求此二次函数的解析式;
(2)求△ABD的面积.
17.如图,用50m长的护栏全部用于建造一块靠墙的长方形花园,写出长方形花园的面积y(m2)与它与墙平行的边的长x(m)之间的函数.
18.如图,抛物线与x轴相交于两点(点在点的左侧),与轴相交于点.为抛物线上一点,横坐标为,且.
⑴求此抛物线的解析式;
⑵当点位于轴下方时,求面积的最大值;
⑶设此抛物线在点与点之间部分(含点和点)最高点与最低点的纵坐标之差为.
①求关于的函数解析式,并写出自变量的取值范围;
②当时,直接写出的面积.
19.某商家销售一款商品,该商品的进价为每件80元,现在的售价为每件145元,每天可销售40件.商场规定每销售一件需支付给商场管理费5元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件.若每件商品降价x元,每天的利润为y元,请完成以下问题的解答.
(Ⅰ)用含x的式子表示:①每件商品的售价为 ▲ 元;②每天的销售量为 ▲ 件;
(Ⅱ)求出y与x之间的函数关系式,并求出售价为多少时利润最大?最大利润是多少元?
20.小明利用暑假20天(8月5日至24日)参与了一家网店经营的社会实践.负责在网络上销售一种新款的SD卡,每张成本价为20元.第x天销售的相关信息如下表所示.
销售量p(张) p=50-x
销售单价q(元/张) q=30+x
(1)请计算哪一天SD卡的销售单价为35元?
(2)在这20天中,在网络上这款销售SD卡在哪一天获得利润最大?这一天赚了多少元?
21.如图,抛物线与轴相交于点,,与轴相交于点C.
(1)求抛物线的函数表达式;
(2)若点为该抛物线对称轴上的一个动点,当时,求点的坐标;
(3)点为该抛物线上的一点,连接,,当时,求点的坐标.
22.已知二次函数y=x2-2mx+m2+3(m是常数).
(1)求证:不论m为何值,该函数的图象与x轴没有公共点;
(2)把该函数的图象沿y轴向下平移多少个单位长度后,得到的函数的图象与x轴只有一个公共点
23.如图,抛物线y1=ax2+bx+与x轴交于点A(﹣3,0),点B,点D是抛物线y1的顶点,过点D作x轴的垂线,垂足为点C(﹣1,0).
(1)求抛物线y1所对应的函数解析式;
(2)如图1,点M是抛物线y1上一点,且位于x轴上方,横坐标为m,连接MC,若∠MCB=∠DAC,求m的值;
(3)如图2,将抛物线y1平移后得到顶点为B的抛物线y2.点P为抛物线y1上的一个动点,过点P作y轴的平行线,交抛物线y2于点Q,过点Q作x轴的平行线,交抛物线y2于点R.当以点P,Q,R为顶点的三角形与△ACD全等时,请直接写出点P的坐标.
一、单选题
1.二次函数y=﹣(x+3)2+2图象的开口方向、对称轴和顶点坐标分别为( )
A.向下,x=3,(3,2) B.向下,x=﹣3,(3,2)
C.向上,x=﹣3,(3,2) D.向下,x=﹣3,(﹣3,2)
2.在同一平面直角坐标系中,一次函数与的图像可能是( )
A. B.
C. D.
3.已知二次函数y=﹣x2﹣2bx+c,当x<2时,y的值随x的增大而增大,则实数b的取值范围是( )
A.b≥﹣1 B.b≤﹣1 C.b≥﹣2 D.b≤﹣2
4.下列二次函数的图象与x轴没有交点的是( )
A.y=-3x2+2x B.y=x2-3x-4
C.y=x2-4x+4 D.y=x2+4x+5
5.如图,抛物线的顶点在的边所在的直线上运动,的顶点的坐标为,点的坐标为,若抛物线与的边、都有公共点,则的取值范围是( )
A. B. C. D.
6.二次函数y=-3x2-6x+5的图像的顶点坐标是( )
A.(-1,8) B.(1,8) C.(-1,2) D.(1,-4)
7.二次函数的图象如图所示,当-1<x<m时,y随x的增大而增大,则m的取值范围是( )
A.m>1 B. C.m>0 D.-1<m<2
8.二次函数()的图象如图所示,则下列结论中正确的有( )个
①;②;③函数的最大值为;④当时,;⑤时,y随x增大而减少
A.4 B.3 C.2 D.1
9.如图所示,二次函数的图象的对称轴是直线,且经过点,有下列结论:①;②为常数);③若,,在该函数图象上,则;④.其中正确的个数是( )
A.1 B.2 C.3 D.4
10.如图,在平面直角坐标系中,抛物线y=ax2+bx+3(a<0)交x轴于A,B两点(B在A左侧),交y轴于点C,且CO=AO,分别以BC,AC为边向外作正方形BCDE、正方形ACGH,记它们的面积分别为S1,S2,△ABC面积记为S3,当S1+S2=6S3时,b的值为( )
A. B. C. D.
二、填空题
11.抛物线 的对称轴为 。
12.点 是二次函数 图象上一点,则-3m2+6m的值为 .
13.已知,抛物线y=ax2+bx+c的部分图象如图,由图可知不等式ax2+bx+c>0的解集为 .
14.如图,抛物线 的对称轴为直线 ,与 轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
① ;② 方程 的两个根是 ;③ ;④当 时, 的取值范围是 ;⑤ 当 时, 随 增大而增大;其中结论正确有 .
15.在平面直角坐标系中,函数y=-x+3a+2(a≠0)和y=x2-ax的图象相交于P,Q两点若P,Q都在x轴的上方,则实数a的取值范围是 。
三、解答题
16.如图,二次函数y=x2+bx+c的图象与x轴交于A(-1,0)、B(3,0)两点,顶点为D.
(1)求此二次函数的解析式;
(2)求△ABD的面积.
17.如图,用50m长的护栏全部用于建造一块靠墙的长方形花园,写出长方形花园的面积y(m2)与它与墙平行的边的长x(m)之间的函数.
18.如图,抛物线与x轴相交于两点(点在点的左侧),与轴相交于点.为抛物线上一点,横坐标为,且.
⑴求此抛物线的解析式;
⑵当点位于轴下方时,求面积的最大值;
⑶设此抛物线在点与点之间部分(含点和点)最高点与最低点的纵坐标之差为.
①求关于的函数解析式,并写出自变量的取值范围;
②当时,直接写出的面积.
19.某商家销售一款商品,该商品的进价为每件80元,现在的售价为每件145元,每天可销售40件.商场规定每销售一件需支付给商场管理费5元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件.若每件商品降价x元,每天的利润为y元,请完成以下问题的解答.
(Ⅰ)用含x的式子表示:①每件商品的售价为 ▲ 元;②每天的销售量为 ▲ 件;
(Ⅱ)求出y与x之间的函数关系式,并求出售价为多少时利润最大?最大利润是多少元?
20.小明利用暑假20天(8月5日至24日)参与了一家网店经营的社会实践.负责在网络上销售一种新款的SD卡,每张成本价为20元.第x天销售的相关信息如下表所示.
销售量p(张) p=50-x
销售单价q(元/张) q=30+x
(1)请计算哪一天SD卡的销售单价为35元?
(2)在这20天中,在网络上这款销售SD卡在哪一天获得利润最大?这一天赚了多少元?
21.如图,抛物线与轴相交于点,,与轴相交于点C.
(1)求抛物线的函数表达式;
(2)若点为该抛物线对称轴上的一个动点,当时,求点的坐标;
(3)点为该抛物线上的一点,连接,,当时,求点的坐标.
22.已知二次函数y=x2-2mx+m2+3(m是常数).
(1)求证:不论m为何值,该函数的图象与x轴没有公共点;
(2)把该函数的图象沿y轴向下平移多少个单位长度后,得到的函数的图象与x轴只有一个公共点
23.如图,抛物线y1=ax2+bx+与x轴交于点A(﹣3,0),点B,点D是抛物线y1的顶点,过点D作x轴的垂线,垂足为点C(﹣1,0).
(1)求抛物线y1所对应的函数解析式;
(2)如图1,点M是抛物线y1上一点,且位于x轴上方,横坐标为m,连接MC,若∠MCB=∠DAC,求m的值;
(3)如图2,将抛物线y1平移后得到顶点为B的抛物线y2.点P为抛物线y1上的一个动点,过点P作y轴的平行线,交抛物线y2于点Q,过点Q作x轴的平行线,交抛物线y2于点R.当以点P,Q,R为顶点的三角形与△ACD全等时,请直接写出点P的坐标.
同课章节目录
