第十一章 三角形 章节检测(无答案) 2024-2025学年人教版数学八年级上册
文档属性
| 名称 | 第十一章 三角形 章节检测(无答案) 2024-2025学年人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 309.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-10 00:00:00 | ||
图片预览

文档简介
第十一章 三角形 章节检测 2024-2025学年人教版数学八年级上册
一、单选题
1.如图所示,直线EFGH,射线分别交直线、于点和点,于点,如果,则( )
A. B. C. D.
2.下列四个命题中,真命题有( )
①两条直线被第三条直线所截,内错角相等;②如果 和 是对顶角,那么 ;③三角形的一个外角大于任何一个内角;④如果 ,那么 .
A.1 个 B.2 个 C.3 个 D.4 个
3.已知在一个凸多边形中,和一个内角相邻的外角与其余内角度数总和为600°,则这个多边形的边数是( )
A.5 B.6 C.7 D.5或6
4.如图,将一副直角三角板按图中所示的位置摆放,两条斜边互相平行,则∠1=( )
A. B. C. D.
5.下列正多边形不能实施平面镶嵌的是( ).
A.正方形 B.正五边形 C.正六边形 D.等边三角形
6.一个多边形的内角和是外角和的3倍,则这个多边形的边数为( )
A.6 B.5 C.4 D.8
7.若一个多边形的内角和是它的外角和的3倍,则该多边形的边数为( )
A.6 B.7 C.9 D.8
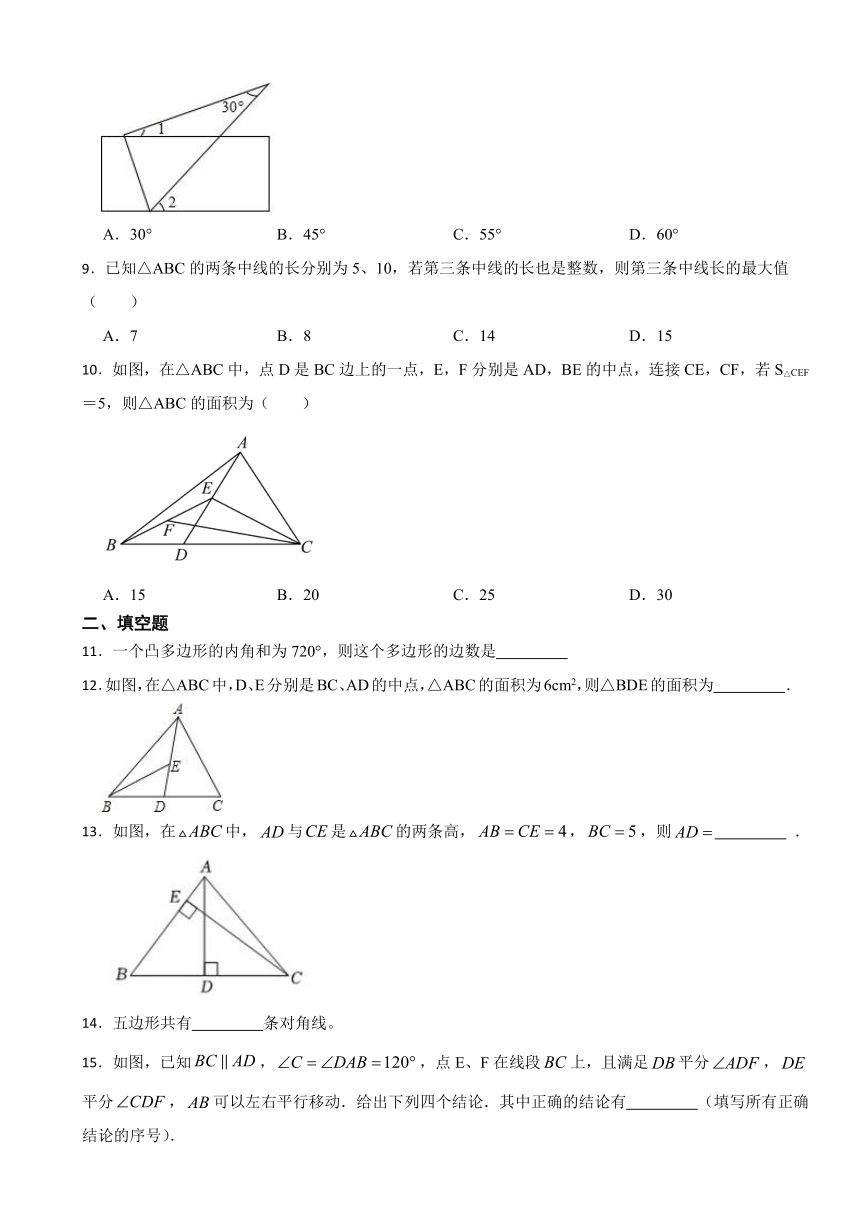
8.如图,将直尺与含30°角的三角尺放在一起,若∠1=25°,则∠2的度数是( )
A.30° B.45° C.55° D.60°
9.已知△ABC的两条中线的长分别为5、10,若第三条中线的长也是整数,则第三条中线长的最大值( )
A.7 B.8 C.14 D.15
10.如图,在△ABC中,点D是BC边上的一点,E,F分别是AD,BE的中点,连接CE,CF,若S△CEF=5,则△ABC的面积为( )
A.15 B.20 C.25 D.30
二、填空题
11.一个凸多边形的内角和为720°,则这个多边形的边数是
12.如图,在△ABC中,D、E分别是BC、AD的中点,△ABC的面积为6cm2,则△BDE的面积为 .
13.如图,在中,与是的两条高,,,则 .
14.五边形共有 条对角线。
15.如图,已知,,点E、F在线段上,且满足平分,平分,可以左右平行移动.给出下列四个结论.其中正确的结论有 (填写所有正确结论的序号).
①;
②;
③;
④
三、解答题
16.如图,,,,求的度数.
17.如图,在中,是的角平分线,,,求的度数.
18.如图,在中,,是的平分线,、、在同一直线上,,,求的度数.
请阅读下列材料,并完成相应任务.
在数学探究课上,老师出了这样一个题:如图,锐角内部有一点,在其两边和上各取任意一点,,连接,,求证:.
小丽的证法 小红的证法
证明: 如图,连接并延长至点,,(依据), 又∵,, ∴. 证明: ∵,,,(量角器测量所得), ∴,(计算所得). ∴(等量代换).
任务:
19.小丽证明过程中的“依据”是指数学定理:______;
20.下列说法正确的是______.
A.小丽的证法用严谨的推理证明了本题结论
B.小丽的证法还需要改变的大小,再进行证明,本题的证明才完整
C.小红的证法用特殊到一般的方法证明了本题结论
D.小红的证法只要将点在的内部任意移动次,重新测量进行验证,就能证明本题结论
21.如图,若点在锐角外部,与相交于点,其余条件不变,原题中结论还成立吗?若成立,请说明理由;若不成立,请写出,,,之间的关系并证明.
22.如图,在 ABC中,AD⊥BC于D,AE平分∠BAC.若∠B=70°,∠C=40°,求∠DAE的度数.
23.已知一个三角形最长边的长为10,另外两边的长分别为和4,周长为,求和的取值范围.
24.如图,在五边形ABCDE中,,求x的值.
25.如图,∠AOB=40°,OC平分∠AOB,点D,E在射线OA,OC上,点P是射线OB上的一个动点,连接DP交射线OC于点F,设∠ODP=x°.
(1)如图1,若DE∥OB.
①∠DEO的度数是 °,当DP⊥OE时,x= ;
②若∠EDF=∠EFD,求x的值;
(2)如图2,若DE⊥OA,是否存在这样的x的值,使得∠EFD=4∠EDF?若存在,求出x的值;若不存在,说明理由.
一、单选题
1.如图所示,直线EFGH,射线分别交直线、于点和点,于点,如果,则( )
A. B. C. D.
2.下列四个命题中,真命题有( )
①两条直线被第三条直线所截,内错角相等;②如果 和 是对顶角,那么 ;③三角形的一个外角大于任何一个内角;④如果 ,那么 .
A.1 个 B.2 个 C.3 个 D.4 个
3.已知在一个凸多边形中,和一个内角相邻的外角与其余内角度数总和为600°,则这个多边形的边数是( )
A.5 B.6 C.7 D.5或6
4.如图,将一副直角三角板按图中所示的位置摆放,两条斜边互相平行,则∠1=( )
A. B. C. D.
5.下列正多边形不能实施平面镶嵌的是( ).
A.正方形 B.正五边形 C.正六边形 D.等边三角形
6.一个多边形的内角和是外角和的3倍,则这个多边形的边数为( )
A.6 B.5 C.4 D.8
7.若一个多边形的内角和是它的外角和的3倍,则该多边形的边数为( )
A.6 B.7 C.9 D.8
8.如图,将直尺与含30°角的三角尺放在一起,若∠1=25°,则∠2的度数是( )
A.30° B.45° C.55° D.60°
9.已知△ABC的两条中线的长分别为5、10,若第三条中线的长也是整数,则第三条中线长的最大值( )
A.7 B.8 C.14 D.15
10.如图,在△ABC中,点D是BC边上的一点,E,F分别是AD,BE的中点,连接CE,CF,若S△CEF=5,则△ABC的面积为( )
A.15 B.20 C.25 D.30
二、填空题
11.一个凸多边形的内角和为720°,则这个多边形的边数是
12.如图,在△ABC中,D、E分别是BC、AD的中点,△ABC的面积为6cm2,则△BDE的面积为 .
13.如图,在中,与是的两条高,,,则 .
14.五边形共有 条对角线。
15.如图,已知,,点E、F在线段上,且满足平分,平分,可以左右平行移动.给出下列四个结论.其中正确的结论有 (填写所有正确结论的序号).
①;
②;
③;
④
三、解答题
16.如图,,,,求的度数.
17.如图,在中,是的角平分线,,,求的度数.
18.如图,在中,,是的平分线,、、在同一直线上,,,求的度数.
请阅读下列材料,并完成相应任务.
在数学探究课上,老师出了这样一个题:如图,锐角内部有一点,在其两边和上各取任意一点,,连接,,求证:.
小丽的证法 小红的证法
证明: 如图,连接并延长至点,,(依据), 又∵,, ∴. 证明: ∵,,,(量角器测量所得), ∴,(计算所得). ∴(等量代换).
任务:
19.小丽证明过程中的“依据”是指数学定理:______;
20.下列说法正确的是______.
A.小丽的证法用严谨的推理证明了本题结论
B.小丽的证法还需要改变的大小,再进行证明,本题的证明才完整
C.小红的证法用特殊到一般的方法证明了本题结论
D.小红的证法只要将点在的内部任意移动次,重新测量进行验证,就能证明本题结论
21.如图,若点在锐角外部,与相交于点,其余条件不变,原题中结论还成立吗?若成立,请说明理由;若不成立,请写出,,,之间的关系并证明.
22.如图,在 ABC中,AD⊥BC于D,AE平分∠BAC.若∠B=70°,∠C=40°,求∠DAE的度数.
23.已知一个三角形最长边的长为10,另外两边的长分别为和4,周长为,求和的取值范围.
24.如图,在五边形ABCDE中,,求x的值.
25.如图,∠AOB=40°,OC平分∠AOB,点D,E在射线OA,OC上,点P是射线OB上的一个动点,连接DP交射线OC于点F,设∠ODP=x°.
(1)如图1,若DE∥OB.
①∠DEO的度数是 °,当DP⊥OE时,x= ;
②若∠EDF=∠EFD,求x的值;
(2)如图2,若DE⊥OA,是否存在这样的x的值,使得∠EFD=4∠EDF?若存在,求出x的值;若不存在,说明理由.
