北师大版数学六年级上册 4 圆的周长 课件(共32张PPT)
文档属性
| 名称 | 北师大版数学六年级上册 4 圆的周长 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 20.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-15 00:00:00 | ||
图片预览








文档简介
(共32张PPT)
圆的周长
瞭望宇宙边缘的天眼,位于贵州省,直径约500米,差不多30个足球场那么大。
车轮直径60厘米
车轮直径40厘米
骑着自行车绕天眼一周,车轮各转几圈呢?怎么求?
几圈即
天眼周长是车轮周长的几倍
圆的周长
预学成果
1. 长方形的周长由( )决定。
2. 正方形的周长由( )决定。
3. 等边三角形的周长由( )决定。
由此猜想:圆的周长可能由( )决定。
预学成果
关键要素
周长
直径、半径
圆的周长 ?
决定
决定
预学成果
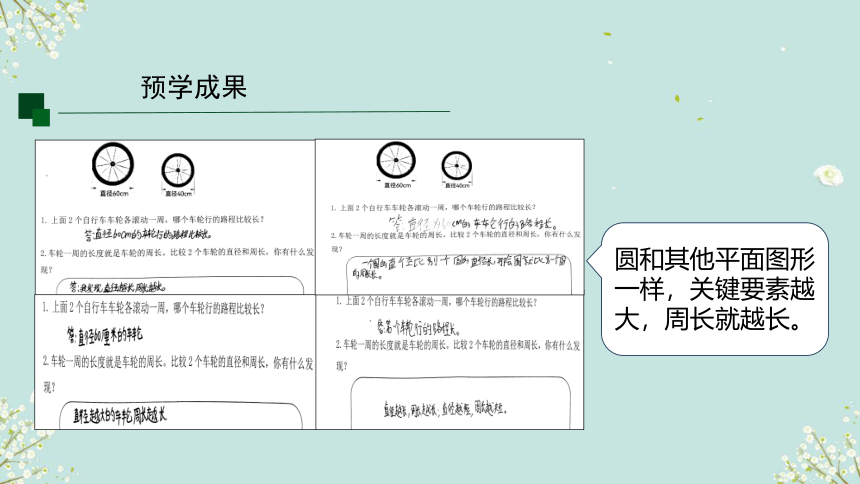
1.上面2个自行车车轮各滚动一周,
哪个车轮行的路程比较长?
2.车轮一周的长度就是车轮的周长。
比较2个车轮的直径和周长,你有什么发现?
预学成果
圆和其他平面图形一样,关键要素越大,周长就越长。
预学成果
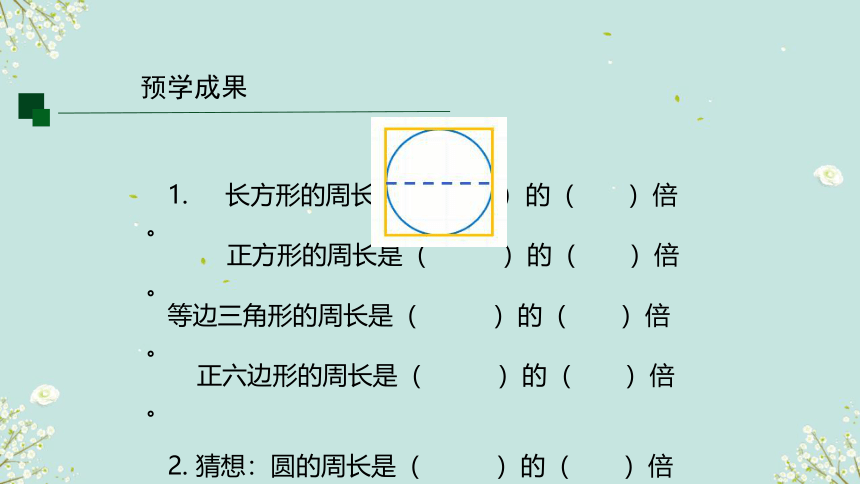
1. 长方形的周长是( )的( )倍。
正方形的周长是( )的( )倍。
等边三角形的周长是( )的( )倍。
正六边形的周长是( )的( )倍。
2. 猜想:圆的周长是( )的( )倍。
预学成果
周长和关键要素有着倍数关系。
活动一:图形相关,推理区间
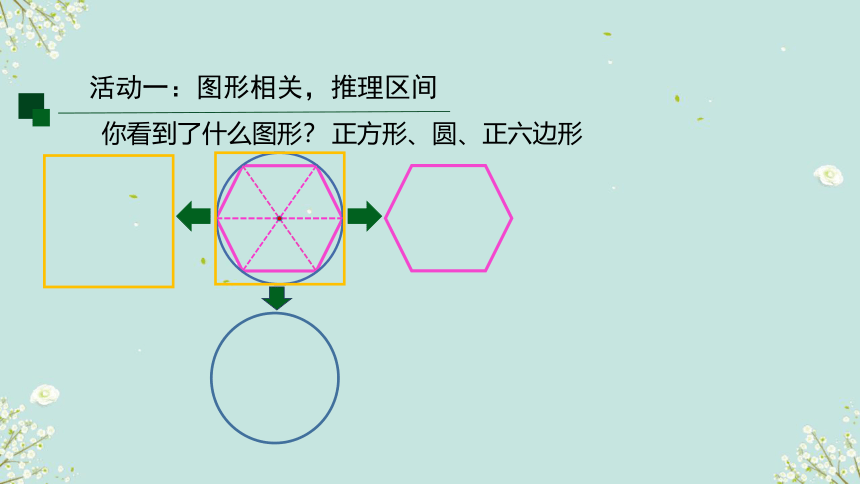
你看到了什么图形?
正方形、圆、正六边形
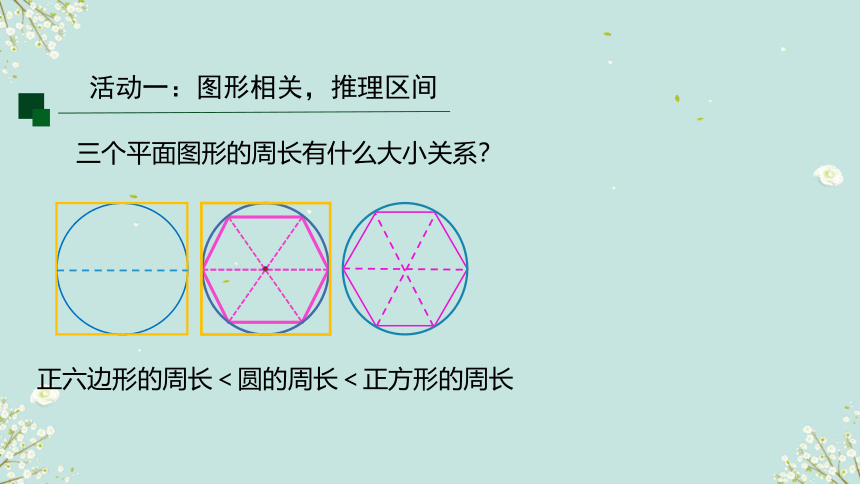
三个平面图形的周长有什么大小关系?
正六边形的周长<圆的周长<正方形的周长
活动一:图形相关,推理区间
各自的关键要素之间有什么关系?
正六边形的边长×6<圆的周长<正方形的边长×4
正方形的边长=圆的直径
正六边形的边长=圆的半径
正六边形的周长=正六边形的边长×6
正方形的周长=正方形的边长×4
活动一:图形相关,推理区间
正六边形的边长×6<圆的周长<正方形的边长×4
( )<圆的周长<( )
正方形的边长=圆的直径
正六边形的边长=圆的半径
三个平面图形关键要素之间的关系:
小支架
半径×6
直径×4
直径×3 <圆的周长<直径×4
正六边形的边长替换为圆的半径
正方形的边长替换为圆的直径
圆的周长是直径的3~4倍
活动一:图形相关,推理区间
圆的周长是直径的3.14倍
d=6cm
d=4cm
活动一:图形相关,推理区间
研究问题:圆的周长是其直径的几倍?
活动要求:
1.测量圆的周长。(测量结果以厘米为单位,保留一位小数)
2.计算出圆的周长是直径的几倍。(结果保留两位小数)
3.将测量和计算结果填入表格。
活动二:实践操作,逐步逼近
序号 直径/cm 周长/cm 周长÷直径
(保留两位小数)
3.14倍
拿一根没弹性的绳子绕圆一周,再量绳子的长度就是圆的周长。
活动二:实践操作,逐步逼近
还可以让圆在尺子上滚,看滚了多远就是圆的周长。
活动二:实践操作,逐步逼近
化曲为直
活动二:实践操作,逐步逼近
研究问题:圆的周长是其直径的几倍?
活动要求:
1.测量圆的周长。(测量结果以厘米为单位,保留一位小数)
2.计算出圆的周长是直径的几倍。(结果保留两位小数)
3.将测量和计算结果填入表格。
活动二:实践操作,逐步逼近
序号 直径/cm 周长/cm 周长÷直径
(保留两位小数)
3.14倍
研究问题:圆的周长是其直径的几倍?
可能是因为绳子没拉紧,松动有误差。
3.14倍
活动二:实践操作,逐步逼近
序号 直径/cm 周长/cm 周长÷直径
(保留两位小数)
1 6 22.3 3.72
2 6 19.3 3.22
3 4 12.1 3.04
研究问题:圆的周长是其直径的几倍?
3.14倍
活动二:实践操作,逐步逼近
序号 直径/cm 周长/cm 周长÷直径
(保留两位小数)
1 6 22.3 3.72
2 6 19.3 3.22
3 4 12.1 3.04
无弹性绳子要拉紧,严丝合缝贴紧圆。
研究问题:圆的周长是其直径的几倍?
序号 直径/cm 周长/cm 周长÷直径
(保留两位小数)
1 6 22.3 3.72
2 6 19.3 3.22
3 4 12.1 3.04
还有可能是滚圆时滑动了,或者滚的超过或不足一周。
3.14倍
活动二:实践操作,逐步逼近
研究问题:圆的周长是其直径的几倍?
在起点画个点作标记,紧紧贴着尺子滚。
3.14倍
活动二:实践操作,逐步逼近
研究问题:圆的周长是其直径的几倍?
活动要求:
1.测量圆的周长。(测量结果以厘米为单位,保留一位小数)
2.计算出圆的周长是直径的几倍。(结果保留两位小数)
3.将测量和计算结果填入表格。
活动二:实践操作,逐步逼近
序号 直径/cm 周长/cm 周长÷直径
(保留两位小数)
3.14倍
研究问题:圆的周长是其直径的几倍?
序号 直径/cm 周长/cm 周长÷直径
(保留两位小数)
4 6 19 3.17
5 4 12.7 3.18
6 6 18.8 3.13
3.14倍
活动二:实践操作,逐步逼近
三倍多一些
研究问题:圆的周长是其直径的几倍?
3.14倍
周三径一
周三径一而有余
刘徽
割圆术
祖冲之
算到小数点后第7位
计算机
活动二:实践操作,逐步逼近
任何一个圆的周长除以直径的商都是一个固定的数,
我们把它叫作圆周率,用字母π表示。
还没有。
π≈3.14
活动二:实践操作,逐步逼近
到现在为止,π算完了吗?
π是一个无限不循环小数
任何一个圆的周长除以直径的商都是一个固定的数,我们把它叫作圆周率,用字母π表示。
圆的周长是直径的π倍
C=πd 或 C=2πr
活动二:实践操作,逐步逼近
骑着自行车绕天眼一周,车轮各转几圈?
车轮直径60厘米
车轮直径40厘米
天眼周长:
3.14×500=1570(米)
大车轮周长:
60×3.14=188.4(厘米)
188.4厘米=1.884米
大车轮转的圈数:
1570÷1.884≈833(圈)
小车轮周长:
40×3.14=125.6(厘米)
125.6厘米=1.256米
小车轮转的圈数:
1570÷1.256=1250(圈)
活动三:运用公式,解决问题
天眼直径500米
πd÷πd1=d÷d1
直接用直径除以直径
商不变规律。
直径是圆的关键要素!
活动三:运用公式,解决问题
骑着自行车绕天眼一周,车轮各转几圈?
小结
圆的周长公式:C=πd 或 C=2πr
正六边形的边长×6<圆的周长<正方形的边长×4
<圆的周长<
半径×6
直径×4
直径×3 <圆的周长<直径×4
正六边形的周长<圆的周长<正方形的周长
圆的周长是直径的三倍多一些
圆的周长是直径的 π 倍
π≈3.14
圆的周长
r
d
圆的周长
瞭望宇宙边缘的天眼,位于贵州省,直径约500米,差不多30个足球场那么大。
车轮直径60厘米
车轮直径40厘米
骑着自行车绕天眼一周,车轮各转几圈呢?怎么求?
几圈即
天眼周长是车轮周长的几倍
圆的周长
预学成果
1. 长方形的周长由( )决定。
2. 正方形的周长由( )决定。
3. 等边三角形的周长由( )决定。
由此猜想:圆的周长可能由( )决定。
预学成果
关键要素
周长
直径、半径
圆的周长 ?
决定
决定
预学成果
1.上面2个自行车车轮各滚动一周,
哪个车轮行的路程比较长?
2.车轮一周的长度就是车轮的周长。
比较2个车轮的直径和周长,你有什么发现?
预学成果
圆和其他平面图形一样,关键要素越大,周长就越长。
预学成果
1. 长方形的周长是( )的( )倍。
正方形的周长是( )的( )倍。
等边三角形的周长是( )的( )倍。
正六边形的周长是( )的( )倍。
2. 猜想:圆的周长是( )的( )倍。
预学成果
周长和关键要素有着倍数关系。
活动一:图形相关,推理区间
你看到了什么图形?
正方形、圆、正六边形
三个平面图形的周长有什么大小关系?
正六边形的周长<圆的周长<正方形的周长
活动一:图形相关,推理区间
各自的关键要素之间有什么关系?
正六边形的边长×6<圆的周长<正方形的边长×4
正方形的边长=圆的直径
正六边形的边长=圆的半径
正六边形的周长=正六边形的边长×6
正方形的周长=正方形的边长×4
活动一:图形相关,推理区间
正六边形的边长×6<圆的周长<正方形的边长×4
( )<圆的周长<( )
正方形的边长=圆的直径
正六边形的边长=圆的半径
三个平面图形关键要素之间的关系:
小支架
半径×6
直径×4
直径×3 <圆的周长<直径×4
正六边形的边长替换为圆的半径
正方形的边长替换为圆的直径
圆的周长是直径的3~4倍
活动一:图形相关,推理区间
圆的周长是直径的3.14倍
d=6cm
d=4cm
活动一:图形相关,推理区间
研究问题:圆的周长是其直径的几倍?
活动要求:
1.测量圆的周长。(测量结果以厘米为单位,保留一位小数)
2.计算出圆的周长是直径的几倍。(结果保留两位小数)
3.将测量和计算结果填入表格。
活动二:实践操作,逐步逼近
序号 直径/cm 周长/cm 周长÷直径
(保留两位小数)
3.14倍
拿一根没弹性的绳子绕圆一周,再量绳子的长度就是圆的周长。
活动二:实践操作,逐步逼近
还可以让圆在尺子上滚,看滚了多远就是圆的周长。
活动二:实践操作,逐步逼近
化曲为直
活动二:实践操作,逐步逼近
研究问题:圆的周长是其直径的几倍?
活动要求:
1.测量圆的周长。(测量结果以厘米为单位,保留一位小数)
2.计算出圆的周长是直径的几倍。(结果保留两位小数)
3.将测量和计算结果填入表格。
活动二:实践操作,逐步逼近
序号 直径/cm 周长/cm 周长÷直径
(保留两位小数)
3.14倍
研究问题:圆的周长是其直径的几倍?
可能是因为绳子没拉紧,松动有误差。
3.14倍
活动二:实践操作,逐步逼近
序号 直径/cm 周长/cm 周长÷直径
(保留两位小数)
1 6 22.3 3.72
2 6 19.3 3.22
3 4 12.1 3.04
研究问题:圆的周长是其直径的几倍?
3.14倍
活动二:实践操作,逐步逼近
序号 直径/cm 周长/cm 周长÷直径
(保留两位小数)
1 6 22.3 3.72
2 6 19.3 3.22
3 4 12.1 3.04
无弹性绳子要拉紧,严丝合缝贴紧圆。
研究问题:圆的周长是其直径的几倍?
序号 直径/cm 周长/cm 周长÷直径
(保留两位小数)
1 6 22.3 3.72
2 6 19.3 3.22
3 4 12.1 3.04
还有可能是滚圆时滑动了,或者滚的超过或不足一周。
3.14倍
活动二:实践操作,逐步逼近
研究问题:圆的周长是其直径的几倍?
在起点画个点作标记,紧紧贴着尺子滚。
3.14倍
活动二:实践操作,逐步逼近
研究问题:圆的周长是其直径的几倍?
活动要求:
1.测量圆的周长。(测量结果以厘米为单位,保留一位小数)
2.计算出圆的周长是直径的几倍。(结果保留两位小数)
3.将测量和计算结果填入表格。
活动二:实践操作,逐步逼近
序号 直径/cm 周长/cm 周长÷直径
(保留两位小数)
3.14倍
研究问题:圆的周长是其直径的几倍?
序号 直径/cm 周长/cm 周长÷直径
(保留两位小数)
4 6 19 3.17
5 4 12.7 3.18
6 6 18.8 3.13
3.14倍
活动二:实践操作,逐步逼近
三倍多一些
研究问题:圆的周长是其直径的几倍?
3.14倍
周三径一
周三径一而有余
刘徽
割圆术
祖冲之
算到小数点后第7位
计算机
活动二:实践操作,逐步逼近
任何一个圆的周长除以直径的商都是一个固定的数,
我们把它叫作圆周率,用字母π表示。
还没有。
π≈3.14
活动二:实践操作,逐步逼近
到现在为止,π算完了吗?
π是一个无限不循环小数
任何一个圆的周长除以直径的商都是一个固定的数,我们把它叫作圆周率,用字母π表示。
圆的周长是直径的π倍
C=πd 或 C=2πr
活动二:实践操作,逐步逼近
骑着自行车绕天眼一周,车轮各转几圈?
车轮直径60厘米
车轮直径40厘米
天眼周长:
3.14×500=1570(米)
大车轮周长:
60×3.14=188.4(厘米)
188.4厘米=1.884米
大车轮转的圈数:
1570÷1.884≈833(圈)
小车轮周长:
40×3.14=125.6(厘米)
125.6厘米=1.256米
小车轮转的圈数:
1570÷1.256=1250(圈)
活动三:运用公式,解决问题
天眼直径500米
πd÷πd1=d÷d1
直接用直径除以直径
商不变规律。
直径是圆的关键要素!
活动三:运用公式,解决问题
骑着自行车绕天眼一周,车轮各转几圈?
小结
圆的周长公式:C=πd 或 C=2πr
正六边形的边长×6<圆的周长<正方形的边长×4
<圆的周长<
半径×6
直径×4
直径×3 <圆的周长<直径×4
正六边形的周长<圆的周长<正方形的周长
圆的周长是直径的三倍多一些
圆的周长是直径的 π 倍
π≈3.14
圆的周长
r
d
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
