小升初分班考高频考点检测卷-数学六年级下册苏教版南京市适用(含解析)
文档属性
| 名称 | 小升初分班考高频考点检测卷-数学六年级下册苏教版南京市适用(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 681.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-11 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
小升初分班考高频考点检测卷-数学六年级下册苏教版南京市适用
一、选择题
1.文文记录自己零用钱的收支情况,收到50元,记作﹢50,支出20元,记作( )。
A.﹢20 B.﹣20 C.﹢30 D.﹣30
2.x=1.5是下列方程中( )的解。
A.x+0.3=1.2 B.1-x=0.5 C.10x+3=18 D.2x-x=3
3.甲杯中有200毫升水,乙杯中有400毫升水。把12克糖放入甲、乙两个杯中,使两杯糖水的含糖率相同。那么应该在甲杯中放入多少克糖?( )
A.6克 B.4克 C.3克 D.2克
4.一个正方体的棱长总和是60厘米,则它的表面积是( )平方厘米。
A.90 B.150 C.135 D.125
5.王奶奶把元钱按年利率存入银行,存期三年。计算到期后她所得的利息,列式应是( )。
A. B.
C. D.
6.阿基米德是古希腊著名的数学家。他发现当“圆柱容球”时,球的体积正好是圆柱体积的,球的表面积也是圆柱表面积的,如图,这个球的表面积是( )。
A. B. C. D.
二、填空题
7.=6∶( )=( )÷24=( )%=0.75。
8.全班46人去公园划船,租12只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船共坐( )人,租的小船共坐( )人。
9.李明的身高是1.5米,他爸爸的身高是1.8米。量得他爸爸在合影照中的身高是7.5厘米,这张合影照的比例尺是( ),合影照中,他爸爸与李明的身高比是( )。
10.把一根长2.4米的圆柱体木材截成同样长的三个圆柱体,表面积增加了12平方分米,这根木料的体积是( )立方米。
11.客车和货车的速度比是7∶5,两车分别从甲、乙两地同时出发,相向而行,经过2.5小时相遇。如果两车分别从甲、乙两地同时出发,同向而行,客车追上货车要用( )小时。
12.为了确保通信安全,信息需要加密传输。现规定加密规则:明文(m,n)加密成密文后是(3m+1,mn)。按照这样的加密规则,明文(2,5)加密后是( , ),密文(10,21)的明文是( , )。
13.有一个电子钟,每到整点响铃一次,每过8分钟亮灯一次。如果这个电子钟在中午12时整的时候既响铃又亮灯,那么下一次既响铃又亮灯的时刻是下午( )时。
14.用小棒按照如下方式摆图形,用2024根小棒可摆( )个正八边形。
三、判断题
15.一个三角形中最小的角是46°,这个三角形一定是锐角三角形。( )
16.两筐芒果相差5千克,正好各卖出10%,现在剩下的仍相差5千克。( )
17.一架飞机从某机场向北偏东50°方向飞行了1200千米,原路返回时要向南偏西50°方向飞行1200千米。( )
18.一批零件,师傅单独做要6小时完成,徒弟单独做要9小时完成。师傅和徒弟的工作效率的最简单的整数比是2∶3。( )
19.一杯纯果汁,小明先喝了半杯,觉得有些甜,就兑满了水,接着他又喝了杯,小明一共喝杯纯果汁和杯水。( )
四、计算题
20.直接写出得数。
860-298= 5.6+1.04= 2-= -= 5×÷5×=
0.8÷1%= = 10÷12= 12.5×2.4= +×2=
21.求未知数x。
9(x+3.7)=49.5
22.灵活计算下面各题。
23.求下面图形阴影部分的面积。(单位:厘米,圆周率取3.14)
五、解答题
24.地球是距离太阳1.5亿公里的第三颗行星,也是人类已知的唯一孕育和支持生命的天体。地球上的海洋面积约为3.6亿平方千米,比陆地面积的2倍还多0.6亿平方千米。地球上的陆地面积约为多少亿平方千米?(用方程解)
25.六三班为庆祝“六一”儿童节装饰教室,按4∶3∶2的比例购买红、黄、绿三种气球共计270个,三种气球各买了多少个?
26.妈妈买了一套850元的服装,裤子的单价是上衣的,上衣和裤子的单价各是多少元?(列方程解答)
27.星星小学美术组把一个长4分米,宽4分米,高6分米的长方体石膏,削成一个最大的圆柱模型,这个圆柱模型的体积是多少立方分米?
28.在比例尺是1∶8000000的地图上,量得A、B两地间的距离是6厘米。甲、乙两辆汽车分别从两地同时出发,相向而行,3小时后相遇。已知甲车平均每小时行驶85千米,乙车平均每小时行驶多少千米?
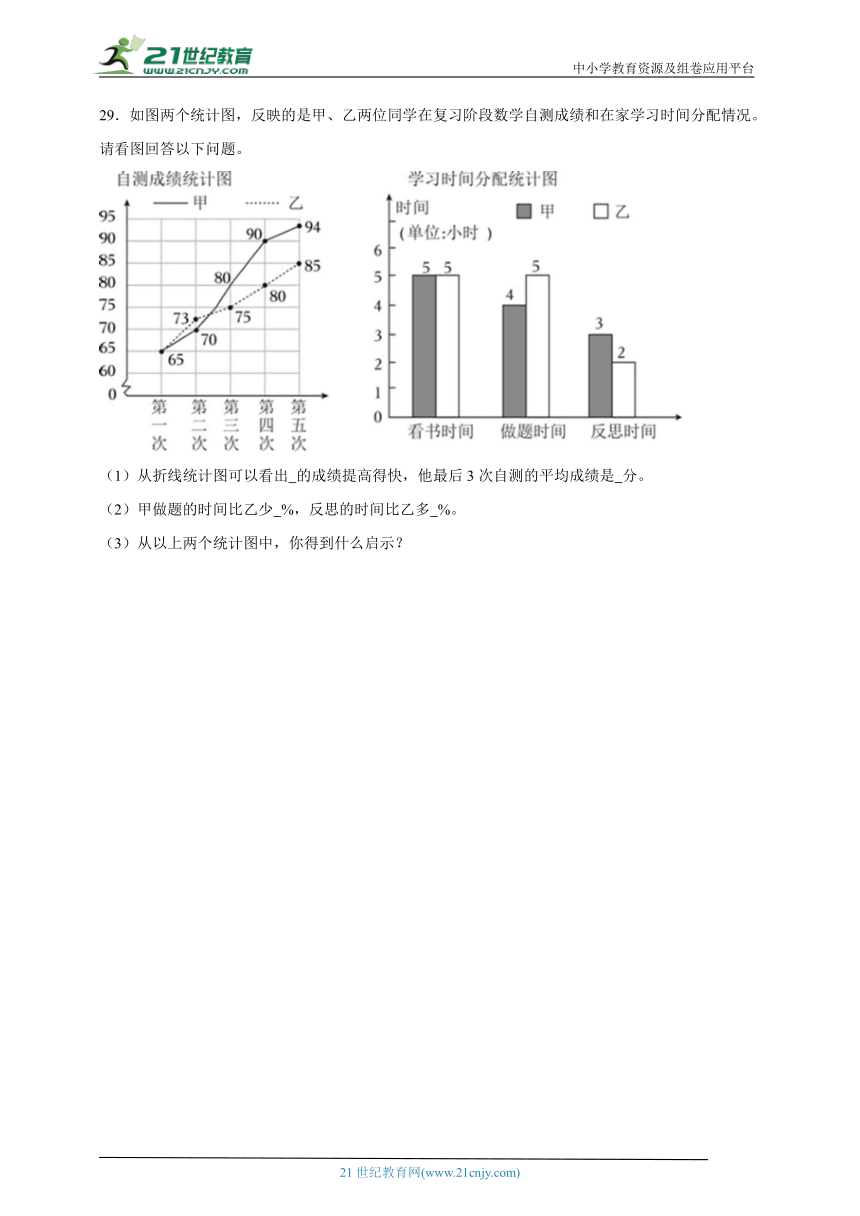
29.如图两个统计图,反映的是甲、乙两位同学在复习阶段数学自测成绩和在家学习时间分配情况。请看图回答以下问题。
(1)从折线统计图可以看出 的成绩提高得快,他最后3次自测的平均成绩是 分。
(2)甲做题的时间比乙少 %,反思的时间比乙多 %。
(3)从以上两个统计图中,你得到什么启示?
参考答案:
1.B
【分析】负数表示和正数意义相反的量。当正数表示收入时,支出应记为负数。
【详解】支出20元,记作﹣20。
故答案为:B
2.C
【分析】把x=1.5分别代入各选项中的方程,如果能使方程成立,说明是该方程的解,否则不是该方程的解。据此解答。
【详解】A.把x=1.5代入方程x+0.3=1.2,左边得:1.5+0.3=1.8,而方程的右边等于1.2,左边不等于右边,所以x=1.5不是方程x+0.3=1.2的解;
B.把x=1.5代入方程1-x=0.5,左边得:1-1.5<0,而方程的右边等于0.5,左边不等于右边,所以x=1.5不是方程1-x=0.5的解;
C.把x=1.5代入方程10x+3=18,左边得:10×1.5+3=18,方程的左边等于右边,所以x=1.5是方程10x+3=18的解;
D.把x=1.5代入方程2x-x=3,左边得:2×1.5-1.5=1.5,而方程的右边等于3,左边不等于右边,所以x=1.5不是方程2x-x=3的解。
故答案为:C
3.B
【分析】含糖率表示糖占糖水的百分之几。从题意可知:甲杯水∶乙杯水=200∶400=1∶2,只要甲杯糖∶乙杯糖=1∶2,就能使两杯糖水的含糖率相同。因此甲杯糖占糖总量的,根据求一个数的几分之几是多少,用乘法计算,用12×即可求出甲杯中放入多少克糖。据此解答。
【详解】200∶400=1∶2
12×
=12×
=4(克)
那么应该在甲杯中放入4克糖。
故答案为:B
4.B
【分析】正方体棱长和=棱长×12,将棱长和除以12,求出棱长。根据正方体表面积=棱长×棱长×6,列式求出它的表面积即可。
【详解】60÷12=5(厘米)
5×5×6=150(平方厘米)
所以,这个正方体的表面积是150平方厘米。
故答案为:B
5.D
【分析】利息=本金×存期×利率,已知本金10000元,年利率2.75%,存期三年,可计算出利息。
【详解】计算到期后她所得的利息,列式应是10000×2.75%×3。
故答案为:D
6.A
【分析】根据圆柱表面积=底面积×2+侧面积,侧面积=底面周长×高,求出圆柱表面积,圆柱表面积×=球的表面积,列式计算即可。
【详解】(πr2×2+2πr×2r)×
=(2πr2+4πr2)×
=6πr2×
=4πr2
这个球的表面积是4πr2。
故答案为:A
7.32;8;18;75
【分析】根据分数化小数的方法是通过将分子除以分母来得到小数形式;分数和比的关系:分子表示比的前项,分母表示比的后项;根据商×除数=被除数这一公式,可以算出被除数;小数和百分数的互化,即小数乘上百分号。
【详解】24÷0.75=32
==(24÷4)÷(32÷4)=6÷8=6∶8
6∶8=(6×3)∶(8×3)=18∶24
0.75×100%=75%
=6∶8=18÷24=75%=0.75。
8. 25 21
【分析】假设12只船全是大船,那么一共可以坐:12×5=60人,这比实际46人多出了:60-46=14人,1只大船比1只小船多坐:5-3=2人,由此即可求得小船有:14÷2=7只,进而再求得大船的只数;最后用船的只数乘每只船能坐的人数,分别求出大船和小船共坐了多少人。
【详解】假设全是大船,则小船有:
(12×5-46)÷(5 3)
=(60-46)÷2
=14÷2
=7(只)
则大船有:12-7=5(只)
5×5=25(人)
7×3=21(人)
租的大船共坐25人,租的小船共坐21人。
9. 1∶24 6∶5
【分析】根据比例尺=图上距离∶实际距离,先求出比例尺,根据图上距离=实际距离×比例尺,求出李明在合照中的身高,即可用他爸爸的身高比上他的身高。
【详解】1.8米=180厘米
1.5米=150厘米
7.5∶180
=(7.5÷7.5)∶(180÷7.5)
=1∶24
150×=6.25(厘米)
7.5∶6.25
=(7.5÷1.25)∶(6.25÷1.25)
=6∶5
所以这张合影照的比例尺是1∶24,合影照中,他爸爸与李明的身高比是6∶5。
10.0.072/
【分析】根据题意可知,截成同样长的三个圆柱体,总共切了2次,则增加了(2×2)个底面积,用12÷(2×2),即可求出一个底面积的面积,再根据公式:圆柱的体积=底面积×高,代入数据即可解答。
【详解】12÷(2×2)
=12÷4
=3(平方分米)
3平方分米=0.03平方米
0.03×2.4=0.072(立方分米)=(立方分米)
即这根木料的体积是0.072(或)立方米。
11.15
【分析】由题可知,客车和货车的速度比是7∶5,则把客车的速度看作7x,货车的速度看作5x,根据路程=速度×时间,用货车和客车的速度和乘相遇的时间,算出甲、乙两地的路程,再用甲、乙两地的总路程除以它们的速度差即可求出客车追上货车要用多少小时。
【详解】(7x+5x)×2.5÷(7x-5x)
=12x×2.5÷2x
=30x÷2x
=15(小时)
客车追上货车要用15小时。
【点睛】熟练掌握路程、速度和时间的关系式,是解答此题的关键。
12. 7 10 3 7
【分析】求明文(2,5)加密后的密文,把m=2,n=5代入3m+1和mn计算即可;求密文(10,21)的明文是多少,可得3m+1=10,求出m的值,再把m的值代入mn=21,求出n的值。
【详解】把m=2,n=5代入3m+1和mn,
3×2+1
=6+1
=7
2×5=10
明文(2,5)加密后是(7,10);
3m+1=10
解:3m+1-1=10-1
3m=9
3m÷3=9÷3
m=3
mn=21
解:3n=21
3n÷3=21÷3
n=7
密文(10,21)的明文是(3,7)。
13.2
【分析】已知电子钟,每到整点响铃一次,每过8分钟亮灯一次,也就是每60分钟响铃一次,现在中午12时整的时候既响铃又亮灯,说明下一次同时响铃又亮灯的间隔时间是60分钟和8分钟的最小公倍数,求两个数的最小公倍数,先将这两个数分别分解质因数,最小公倍数是两个数公有的质因数和各自独有的质因数的乘积。再用起始时间加上经过的时间,即可推算出下一次既响铃又亮灯的时刻。
【详解】60=2×2×3×5
8=2×2×2
60和8的最小公倍数是2×2×2×3×5=120
120分钟=2小时
12时+2小时=14时
14时就是下午2时。
下一次既响铃又亮灯的时刻是下午2时。
14.289
【分析】摆1个正八边形需要的小棒数为8根,即7×1+1;摆2个正八边形需要的小棒数为15根,即7×2+1;摆3个正八边形需要的小棒数为22根,即7×3+1;……摆n个正八边形需要的小棒数为:7n+1。求用2024根小棒可摆多少个正八边形,就是当7n+1=2024时,求n的值。
【详解】摆n个正八边形需要的小棒数为:7n+1,由此列方程得:
7n+1=2024
解:7n+1-1=2024-1
7n=2023
7n÷7=2023÷7
n=289
所以用2024根小棒可摆289个正八边形。
15.√
【分析】有一个角是直角的三角形是直角三角形;三个角都是锐角的三角形是锐角三角形;有一个角是钝角的三角形是钝角三角形;
根据题意可知,该三角形中最小的角是46°,而三角形内角和为180°,一个三角形中至少有两个锐角,所以另外一个锐角一定不小于46°,同时另外一个锐角越小,剩下的那个角就越大,依据最大的角的度数进行判断三角形类别即可。
【详解】由分析可得:
在一个三角形中至少有两个锐角,同时该三角形中最小的角是46°,另外一个锐角一定不小于46°,则46°+46°=92°,三角形内角和为180°,180°-92°=88°,所以这个三角形不可能是直角三角形,也不可能是钝角三角形,其一定是锐角三角形。
故答案为:√
16.×
【分析】两筐芒果相差5千克,可以假设一筐芒果是10千克,则另外一筐芒果为10+5=15(千克),分别将两筐芒果的千克数看作单位“1”,各自卖出10%,则剩下的都为各自千克数的(1-10%),根据百分数乘法的意义,求一个数的百分之几是多少用乘法,即分别用两筐芒果的千克数乘(1-10%)可求出此时两筐芒果剩下的千克数,再相减即为相差的千克数,和5千克比较即可。
【详解】由分析可得:
假设一筐芒果千克数为10千克,则另外一筐芒果为10+5=15(千克),
10×(1-10%)
=10×0.9
=9(千克)
15×(1-10%)
=15×0.9
=13.5(千克)
13.5-9=4.5(千克)
4.5千克≠5千克
故答案为:×
17.√
【分析】根据位置的相对性可知:位置相对的两个物体所在的方向相反、角度相同、距离不变;据此解答。
【详解】由分析可得:一架飞机从某机场向北偏东50°方向飞行了1200千米,原路返回时要向南偏西50°方向飞行1200千米,原题说法正确。
故答案为:√
18.×
【分析】根据题意,把工作总量看作单位“1”,结合工作效率=工作总量÷工作时间,分别算出师傅和徒弟的工作效率,用师傅的工作效率比上徒弟的工作效率即可。
【详解】师傅的工作效率:1÷6=
徒弟的工作效率:1÷9=
∶
=
=9∶6
=(9÷3)∶(6÷3)
=3∶2
所以师傅和徒弟的工作效率的最简单的整数比是3∶2。原题说法错误。
故答案为:×
19.√
【分析】把这杯果汁的量看作单位“1”,喝了半杯,即喝了杯纯果汁;兑满水,接着又喝了半杯,这时喝了纯果汁的杯的,即(×)杯,同理,也喝了(×)杯水。再把两次喝的果汁杯数相加。
【详解】+×
=+
=(杯)
×=(杯)
即,小明一共喝杯纯果汁和杯水,原题说法正确。
故答案为:√
20.562;6.64;;0.05;;
80;6;;30;
【详解】略
21.x=1.8;x=
【分析】根据等式的性质2,方程两边同时除以9,再根据等式的性质1,方程两边同时减去3.7;
根据比例的基本性质,先把比例化为方程:x=,再根据等式的性质2,方程两边同时乘3。
【详解】9(x+3.7)=49.5
解:x+3.7=49.5÷9
x+3.7=5.5
x=5.5-3.7
x=1.8
解:x=
x=
x=×3
x=
22.12
【解析】略
23.10.75平方厘米
【分析】阴影部分的面积等于三角形的面积减去三个扇形的面积,三角形内角和是180度,所以三个扇形的面积可以拼在一起形成一个圆心角为180度的扇形(即半圆),根据三角形面积公式:面积=底×高÷2,圆的面积公式:面积=π×半径2,代入数据,即可解答。
【详解】(5+5)×(5+5)÷2-3.14×52÷2
=10×10÷2-3.14×25÷2
=100÷2-78.5÷2
=50-39.25
=10.75(平方厘米)
阴影部分面积是10.75平方厘米。
24.1.5亿平方千米
【分析】设地球上的陆地面积约为x亿平方千米,根据等量关系:地球上的陆地面积×2+0.6=3.6亿平方千米,列方程解答即可。
【详解】解:设地球上的陆地面积约为x亿平方千米。
2x+0.6=3.6
2x+0.6-0.6=3.6-0.6
2x=3
2x÷2=3÷2
x=1.5
答:地球上的陆地面积约为1.5亿平方千米。
25.120个;90个;60个
【分析】以气球总个数为单位“1”, 红、黄、绿三种气球分别各占气球总个数的、、。根据求一个数的几分之几是多少,用乘法计算。用气球总个数分别乘红、黄、绿的对应分率,即可求出红、黄、绿的个数各是多少。据此解答。
【详解】红色:
270×
=270×
=120(个)
黄色:
270×
=270×
=90(个)
绿色:
270×
=270×
=60(个)
答:红色120个,黄色90个,绿色60个。
26.上衣510元;裤子340元
【分析】裤子的单价是上衣的,设上衣为元,则裤子为元,一共850元,可以列出方程+=850,根据等式的性质,两边同时除以一个数等式不变,解方程求出上衣的单价,再用850减去上衣的单价求出裤子的单价即可。
【详解】解:设上衣单价是元。
+=850
=850
=510
裤子单价:850-510=340(元)
答:上衣的单价是510元,裤子的单价是340元。
27.75.36立方分米
【分析】长方体的长4分米,宽4分米,所以长方体的底面是正方形,因此要将长方体削成一个最大的圆柱,这个圆柱的底面直经等于长方体的底面边长,圆柱的高等于长方体的高,根据圆柱的体积公式:V=πr2h,把数据代入公式解答即可。
【详解】半径:4÷2=2(分米)
圆柱体积为:
3.14×22×6
=3.14×4×6
=12.56×6
=75.36(立方分米)
答:这个圆柱模型的最大体积是75.36立方分米。
28.75千米
【分析】图上距离和比例尺已知,依据“图上距离÷比例尺=实际距离”即可求出两地的实际距离。再根据“速度和=路程÷相遇时间”即可求出两车的速度和,再减甲车的速度,即可求出乙车的速度,据此解答。
【详解】6÷=48000000(厘米)
48000000厘米=480千米
480÷3=160(千米/时)
160-85=75(千米/时)
答:乙车平均每小时行驶75千米。
29.(1)甲;88
(2)20;50
(3)见详解
【分析】(1)从折线统计图可以看出甲的成绩提高得快,然后把最后3次自测的成绩相加求和,再除以3,即可求出他最后3次自测的平均成绩是多少分;
(2)用甲做题时间与乙做题时间的差除以乙做题的时间,即可求出甲做题的时间比乙少百分之几;用乙反思的时间与甲反思的时间的差除以乙反思的时间,即可求出反思的时间比乙多百分之几;
(3)从以上两个统计图中可以看出甲的成绩提高得快,因为甲用来反思的时间多,这样就能找出自己存在的问题并改正。(答案不唯一)
【详解】(1)(80+90+94)÷3
=(170+94)÷3
=264÷3
=88(分)
从折线统计图可以看出甲的成绩提高得快。他最后3次自测的平均成绩是88分。
(2)(5-4)÷5
=1÷5
=20%
(3-2)÷2
=1÷2
=50%
甲做题的时间比乙少20%,反思的时间比乙多50%。
(3)从以上两个统计图中,我得到的启示是:多思考,成绩提高得快,因为多反思能找出自己存在的问题并改正。(答案不唯一)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
小升初分班考高频考点检测卷-数学六年级下册苏教版南京市适用
一、选择题
1.文文记录自己零用钱的收支情况,收到50元,记作﹢50,支出20元,记作( )。
A.﹢20 B.﹣20 C.﹢30 D.﹣30
2.x=1.5是下列方程中( )的解。
A.x+0.3=1.2 B.1-x=0.5 C.10x+3=18 D.2x-x=3
3.甲杯中有200毫升水,乙杯中有400毫升水。把12克糖放入甲、乙两个杯中,使两杯糖水的含糖率相同。那么应该在甲杯中放入多少克糖?( )
A.6克 B.4克 C.3克 D.2克
4.一个正方体的棱长总和是60厘米,则它的表面积是( )平方厘米。
A.90 B.150 C.135 D.125
5.王奶奶把元钱按年利率存入银行,存期三年。计算到期后她所得的利息,列式应是( )。
A. B.
C. D.
6.阿基米德是古希腊著名的数学家。他发现当“圆柱容球”时,球的体积正好是圆柱体积的,球的表面积也是圆柱表面积的,如图,这个球的表面积是( )。
A. B. C. D.
二、填空题
7.=6∶( )=( )÷24=( )%=0.75。
8.全班46人去公园划船,租12只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船共坐( )人,租的小船共坐( )人。
9.李明的身高是1.5米,他爸爸的身高是1.8米。量得他爸爸在合影照中的身高是7.5厘米,这张合影照的比例尺是( ),合影照中,他爸爸与李明的身高比是( )。
10.把一根长2.4米的圆柱体木材截成同样长的三个圆柱体,表面积增加了12平方分米,这根木料的体积是( )立方米。
11.客车和货车的速度比是7∶5,两车分别从甲、乙两地同时出发,相向而行,经过2.5小时相遇。如果两车分别从甲、乙两地同时出发,同向而行,客车追上货车要用( )小时。
12.为了确保通信安全,信息需要加密传输。现规定加密规则:明文(m,n)加密成密文后是(3m+1,mn)。按照这样的加密规则,明文(2,5)加密后是( , ),密文(10,21)的明文是( , )。
13.有一个电子钟,每到整点响铃一次,每过8分钟亮灯一次。如果这个电子钟在中午12时整的时候既响铃又亮灯,那么下一次既响铃又亮灯的时刻是下午( )时。
14.用小棒按照如下方式摆图形,用2024根小棒可摆( )个正八边形。
三、判断题
15.一个三角形中最小的角是46°,这个三角形一定是锐角三角形。( )
16.两筐芒果相差5千克,正好各卖出10%,现在剩下的仍相差5千克。( )
17.一架飞机从某机场向北偏东50°方向飞行了1200千米,原路返回时要向南偏西50°方向飞行1200千米。( )
18.一批零件,师傅单独做要6小时完成,徒弟单独做要9小时完成。师傅和徒弟的工作效率的最简单的整数比是2∶3。( )
19.一杯纯果汁,小明先喝了半杯,觉得有些甜,就兑满了水,接着他又喝了杯,小明一共喝杯纯果汁和杯水。( )
四、计算题
20.直接写出得数。
860-298= 5.6+1.04= 2-= -= 5×÷5×=
0.8÷1%= = 10÷12= 12.5×2.4= +×2=
21.求未知数x。
9(x+3.7)=49.5
22.灵活计算下面各题。
23.求下面图形阴影部分的面积。(单位:厘米,圆周率取3.14)
五、解答题
24.地球是距离太阳1.5亿公里的第三颗行星,也是人类已知的唯一孕育和支持生命的天体。地球上的海洋面积约为3.6亿平方千米,比陆地面积的2倍还多0.6亿平方千米。地球上的陆地面积约为多少亿平方千米?(用方程解)
25.六三班为庆祝“六一”儿童节装饰教室,按4∶3∶2的比例购买红、黄、绿三种气球共计270个,三种气球各买了多少个?
26.妈妈买了一套850元的服装,裤子的单价是上衣的,上衣和裤子的单价各是多少元?(列方程解答)
27.星星小学美术组把一个长4分米,宽4分米,高6分米的长方体石膏,削成一个最大的圆柱模型,这个圆柱模型的体积是多少立方分米?
28.在比例尺是1∶8000000的地图上,量得A、B两地间的距离是6厘米。甲、乙两辆汽车分别从两地同时出发,相向而行,3小时后相遇。已知甲车平均每小时行驶85千米,乙车平均每小时行驶多少千米?
29.如图两个统计图,反映的是甲、乙两位同学在复习阶段数学自测成绩和在家学习时间分配情况。请看图回答以下问题。
(1)从折线统计图可以看出 的成绩提高得快,他最后3次自测的平均成绩是 分。
(2)甲做题的时间比乙少 %,反思的时间比乙多 %。
(3)从以上两个统计图中,你得到什么启示?
参考答案:
1.B
【分析】负数表示和正数意义相反的量。当正数表示收入时,支出应记为负数。
【详解】支出20元,记作﹣20。
故答案为:B
2.C
【分析】把x=1.5分别代入各选项中的方程,如果能使方程成立,说明是该方程的解,否则不是该方程的解。据此解答。
【详解】A.把x=1.5代入方程x+0.3=1.2,左边得:1.5+0.3=1.8,而方程的右边等于1.2,左边不等于右边,所以x=1.5不是方程x+0.3=1.2的解;
B.把x=1.5代入方程1-x=0.5,左边得:1-1.5<0,而方程的右边等于0.5,左边不等于右边,所以x=1.5不是方程1-x=0.5的解;
C.把x=1.5代入方程10x+3=18,左边得:10×1.5+3=18,方程的左边等于右边,所以x=1.5是方程10x+3=18的解;
D.把x=1.5代入方程2x-x=3,左边得:2×1.5-1.5=1.5,而方程的右边等于3,左边不等于右边,所以x=1.5不是方程2x-x=3的解。
故答案为:C
3.B
【分析】含糖率表示糖占糖水的百分之几。从题意可知:甲杯水∶乙杯水=200∶400=1∶2,只要甲杯糖∶乙杯糖=1∶2,就能使两杯糖水的含糖率相同。因此甲杯糖占糖总量的,根据求一个数的几分之几是多少,用乘法计算,用12×即可求出甲杯中放入多少克糖。据此解答。
【详解】200∶400=1∶2
12×
=12×
=4(克)
那么应该在甲杯中放入4克糖。
故答案为:B
4.B
【分析】正方体棱长和=棱长×12,将棱长和除以12,求出棱长。根据正方体表面积=棱长×棱长×6,列式求出它的表面积即可。
【详解】60÷12=5(厘米)
5×5×6=150(平方厘米)
所以,这个正方体的表面积是150平方厘米。
故答案为:B
5.D
【分析】利息=本金×存期×利率,已知本金10000元,年利率2.75%,存期三年,可计算出利息。
【详解】计算到期后她所得的利息,列式应是10000×2.75%×3。
故答案为:D
6.A
【分析】根据圆柱表面积=底面积×2+侧面积,侧面积=底面周长×高,求出圆柱表面积,圆柱表面积×=球的表面积,列式计算即可。
【详解】(πr2×2+2πr×2r)×
=(2πr2+4πr2)×
=6πr2×
=4πr2
这个球的表面积是4πr2。
故答案为:A
7.32;8;18;75
【分析】根据分数化小数的方法是通过将分子除以分母来得到小数形式;分数和比的关系:分子表示比的前项,分母表示比的后项;根据商×除数=被除数这一公式,可以算出被除数;小数和百分数的互化,即小数乘上百分号。
【详解】24÷0.75=32
==(24÷4)÷(32÷4)=6÷8=6∶8
6∶8=(6×3)∶(8×3)=18∶24
0.75×100%=75%
=6∶8=18÷24=75%=0.75。
8. 25 21
【分析】假设12只船全是大船,那么一共可以坐:12×5=60人,这比实际46人多出了:60-46=14人,1只大船比1只小船多坐:5-3=2人,由此即可求得小船有:14÷2=7只,进而再求得大船的只数;最后用船的只数乘每只船能坐的人数,分别求出大船和小船共坐了多少人。
【详解】假设全是大船,则小船有:
(12×5-46)÷(5 3)
=(60-46)÷2
=14÷2
=7(只)
则大船有:12-7=5(只)
5×5=25(人)
7×3=21(人)
租的大船共坐25人,租的小船共坐21人。
9. 1∶24 6∶5
【分析】根据比例尺=图上距离∶实际距离,先求出比例尺,根据图上距离=实际距离×比例尺,求出李明在合照中的身高,即可用他爸爸的身高比上他的身高。
【详解】1.8米=180厘米
1.5米=150厘米
7.5∶180
=(7.5÷7.5)∶(180÷7.5)
=1∶24
150×=6.25(厘米)
7.5∶6.25
=(7.5÷1.25)∶(6.25÷1.25)
=6∶5
所以这张合影照的比例尺是1∶24,合影照中,他爸爸与李明的身高比是6∶5。
10.0.072/
【分析】根据题意可知,截成同样长的三个圆柱体,总共切了2次,则增加了(2×2)个底面积,用12÷(2×2),即可求出一个底面积的面积,再根据公式:圆柱的体积=底面积×高,代入数据即可解答。
【详解】12÷(2×2)
=12÷4
=3(平方分米)
3平方分米=0.03平方米
0.03×2.4=0.072(立方分米)=(立方分米)
即这根木料的体积是0.072(或)立方米。
11.15
【分析】由题可知,客车和货车的速度比是7∶5,则把客车的速度看作7x,货车的速度看作5x,根据路程=速度×时间,用货车和客车的速度和乘相遇的时间,算出甲、乙两地的路程,再用甲、乙两地的总路程除以它们的速度差即可求出客车追上货车要用多少小时。
【详解】(7x+5x)×2.5÷(7x-5x)
=12x×2.5÷2x
=30x÷2x
=15(小时)
客车追上货车要用15小时。
【点睛】熟练掌握路程、速度和时间的关系式,是解答此题的关键。
12. 7 10 3 7
【分析】求明文(2,5)加密后的密文,把m=2,n=5代入3m+1和mn计算即可;求密文(10,21)的明文是多少,可得3m+1=10,求出m的值,再把m的值代入mn=21,求出n的值。
【详解】把m=2,n=5代入3m+1和mn,
3×2+1
=6+1
=7
2×5=10
明文(2,5)加密后是(7,10);
3m+1=10
解:3m+1-1=10-1
3m=9
3m÷3=9÷3
m=3
mn=21
解:3n=21
3n÷3=21÷3
n=7
密文(10,21)的明文是(3,7)。
13.2
【分析】已知电子钟,每到整点响铃一次,每过8分钟亮灯一次,也就是每60分钟响铃一次,现在中午12时整的时候既响铃又亮灯,说明下一次同时响铃又亮灯的间隔时间是60分钟和8分钟的最小公倍数,求两个数的最小公倍数,先将这两个数分别分解质因数,最小公倍数是两个数公有的质因数和各自独有的质因数的乘积。再用起始时间加上经过的时间,即可推算出下一次既响铃又亮灯的时刻。
【详解】60=2×2×3×5
8=2×2×2
60和8的最小公倍数是2×2×2×3×5=120
120分钟=2小时
12时+2小时=14时
14时就是下午2时。
下一次既响铃又亮灯的时刻是下午2时。
14.289
【分析】摆1个正八边形需要的小棒数为8根,即7×1+1;摆2个正八边形需要的小棒数为15根,即7×2+1;摆3个正八边形需要的小棒数为22根,即7×3+1;……摆n个正八边形需要的小棒数为:7n+1。求用2024根小棒可摆多少个正八边形,就是当7n+1=2024时,求n的值。
【详解】摆n个正八边形需要的小棒数为:7n+1,由此列方程得:
7n+1=2024
解:7n+1-1=2024-1
7n=2023
7n÷7=2023÷7
n=289
所以用2024根小棒可摆289个正八边形。
15.√
【分析】有一个角是直角的三角形是直角三角形;三个角都是锐角的三角形是锐角三角形;有一个角是钝角的三角形是钝角三角形;
根据题意可知,该三角形中最小的角是46°,而三角形内角和为180°,一个三角形中至少有两个锐角,所以另外一个锐角一定不小于46°,同时另外一个锐角越小,剩下的那个角就越大,依据最大的角的度数进行判断三角形类别即可。
【详解】由分析可得:
在一个三角形中至少有两个锐角,同时该三角形中最小的角是46°,另外一个锐角一定不小于46°,则46°+46°=92°,三角形内角和为180°,180°-92°=88°,所以这个三角形不可能是直角三角形,也不可能是钝角三角形,其一定是锐角三角形。
故答案为:√
16.×
【分析】两筐芒果相差5千克,可以假设一筐芒果是10千克,则另外一筐芒果为10+5=15(千克),分别将两筐芒果的千克数看作单位“1”,各自卖出10%,则剩下的都为各自千克数的(1-10%),根据百分数乘法的意义,求一个数的百分之几是多少用乘法,即分别用两筐芒果的千克数乘(1-10%)可求出此时两筐芒果剩下的千克数,再相减即为相差的千克数,和5千克比较即可。
【详解】由分析可得:
假设一筐芒果千克数为10千克,则另外一筐芒果为10+5=15(千克),
10×(1-10%)
=10×0.9
=9(千克)
15×(1-10%)
=15×0.9
=13.5(千克)
13.5-9=4.5(千克)
4.5千克≠5千克
故答案为:×
17.√
【分析】根据位置的相对性可知:位置相对的两个物体所在的方向相反、角度相同、距离不变;据此解答。
【详解】由分析可得:一架飞机从某机场向北偏东50°方向飞行了1200千米,原路返回时要向南偏西50°方向飞行1200千米,原题说法正确。
故答案为:√
18.×
【分析】根据题意,把工作总量看作单位“1”,结合工作效率=工作总量÷工作时间,分别算出师傅和徒弟的工作效率,用师傅的工作效率比上徒弟的工作效率即可。
【详解】师傅的工作效率:1÷6=
徒弟的工作效率:1÷9=
∶
=
=9∶6
=(9÷3)∶(6÷3)
=3∶2
所以师傅和徒弟的工作效率的最简单的整数比是3∶2。原题说法错误。
故答案为:×
19.√
【分析】把这杯果汁的量看作单位“1”,喝了半杯,即喝了杯纯果汁;兑满水,接着又喝了半杯,这时喝了纯果汁的杯的,即(×)杯,同理,也喝了(×)杯水。再把两次喝的果汁杯数相加。
【详解】+×
=+
=(杯)
×=(杯)
即,小明一共喝杯纯果汁和杯水,原题说法正确。
故答案为:√
20.562;6.64;;0.05;;
80;6;;30;
【详解】略
21.x=1.8;x=
【分析】根据等式的性质2,方程两边同时除以9,再根据等式的性质1,方程两边同时减去3.7;
根据比例的基本性质,先把比例化为方程:x=,再根据等式的性质2,方程两边同时乘3。
【详解】9(x+3.7)=49.5
解:x+3.7=49.5÷9
x+3.7=5.5
x=5.5-3.7
x=1.8
解:x=
x=
x=×3
x=
22.12
【解析】略
23.10.75平方厘米
【分析】阴影部分的面积等于三角形的面积减去三个扇形的面积,三角形内角和是180度,所以三个扇形的面积可以拼在一起形成一个圆心角为180度的扇形(即半圆),根据三角形面积公式:面积=底×高÷2,圆的面积公式:面积=π×半径2,代入数据,即可解答。
【详解】(5+5)×(5+5)÷2-3.14×52÷2
=10×10÷2-3.14×25÷2
=100÷2-78.5÷2
=50-39.25
=10.75(平方厘米)
阴影部分面积是10.75平方厘米。
24.1.5亿平方千米
【分析】设地球上的陆地面积约为x亿平方千米,根据等量关系:地球上的陆地面积×2+0.6=3.6亿平方千米,列方程解答即可。
【详解】解:设地球上的陆地面积约为x亿平方千米。
2x+0.6=3.6
2x+0.6-0.6=3.6-0.6
2x=3
2x÷2=3÷2
x=1.5
答:地球上的陆地面积约为1.5亿平方千米。
25.120个;90个;60个
【分析】以气球总个数为单位“1”, 红、黄、绿三种气球分别各占气球总个数的、、。根据求一个数的几分之几是多少,用乘法计算。用气球总个数分别乘红、黄、绿的对应分率,即可求出红、黄、绿的个数各是多少。据此解答。
【详解】红色:
270×
=270×
=120(个)
黄色:
270×
=270×
=90(个)
绿色:
270×
=270×
=60(个)
答:红色120个,黄色90个,绿色60个。
26.上衣510元;裤子340元
【分析】裤子的单价是上衣的,设上衣为元,则裤子为元,一共850元,可以列出方程+=850,根据等式的性质,两边同时除以一个数等式不变,解方程求出上衣的单价,再用850减去上衣的单价求出裤子的单价即可。
【详解】解:设上衣单价是元。
+=850
=850
=510
裤子单价:850-510=340(元)
答:上衣的单价是510元,裤子的单价是340元。
27.75.36立方分米
【分析】长方体的长4分米,宽4分米,所以长方体的底面是正方形,因此要将长方体削成一个最大的圆柱,这个圆柱的底面直经等于长方体的底面边长,圆柱的高等于长方体的高,根据圆柱的体积公式:V=πr2h,把数据代入公式解答即可。
【详解】半径:4÷2=2(分米)
圆柱体积为:
3.14×22×6
=3.14×4×6
=12.56×6
=75.36(立方分米)
答:这个圆柱模型的最大体积是75.36立方分米。
28.75千米
【分析】图上距离和比例尺已知,依据“图上距离÷比例尺=实际距离”即可求出两地的实际距离。再根据“速度和=路程÷相遇时间”即可求出两车的速度和,再减甲车的速度,即可求出乙车的速度,据此解答。
【详解】6÷=48000000(厘米)
48000000厘米=480千米
480÷3=160(千米/时)
160-85=75(千米/时)
答:乙车平均每小时行驶75千米。
29.(1)甲;88
(2)20;50
(3)见详解
【分析】(1)从折线统计图可以看出甲的成绩提高得快,然后把最后3次自测的成绩相加求和,再除以3,即可求出他最后3次自测的平均成绩是多少分;
(2)用甲做题时间与乙做题时间的差除以乙做题的时间,即可求出甲做题的时间比乙少百分之几;用乙反思的时间与甲反思的时间的差除以乙反思的时间,即可求出反思的时间比乙多百分之几;
(3)从以上两个统计图中可以看出甲的成绩提高得快,因为甲用来反思的时间多,这样就能找出自己存在的问题并改正。(答案不唯一)
【详解】(1)(80+90+94)÷3
=(170+94)÷3
=264÷3
=88(分)
从折线统计图可以看出甲的成绩提高得快。他最后3次自测的平均成绩是88分。
(2)(5-4)÷5
=1÷5
=20%
(3-2)÷2
=1÷2
=50%
甲做题的时间比乙少20%,反思的时间比乙多50%。
(3)从以上两个统计图中,我得到的启示是:多思考,成绩提高得快,因为多反思能找出自己存在的问题并改正。(答案不唯一)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
