人教版九年级上册数学第二十二章二次函数应用题训练(含解析)
文档属性
| 名称 | 人教版九年级上册数学第二十二章二次函数应用题训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-11 07:01:12 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
人教版九年级上册数学第二十二章二次函数应用题训练
1.超市销售某品牌洗手液,进价为每瓶元在销售过程中发现,每天销售量瓶与每瓶售价元之间满足一次函数关系其中,且为整数,当每瓶洗手液的售价是元时,每天销售量为瓶;当每瓶洗手液的售价是元时,每天销售量为瓶.
(1)求与之间的函数关系式;
(2)超市要想使该品牌洗手液的销售利润平均每天达到元,每瓶洗手液的定价应为多少元?
(3)设超市销售该品牌洗手液每天销售利润为元,当每瓶洗手液的售价定为多少元时,超市销售该品牌洗手液每天销售利润最大,最大利润是多少元?
2.消毒洗手液与百姓生活息息相关,某药店的消毒洗手液很畅销.已知该消毒洗手液的进价为每瓶22元,经市场调查,每天洗手液的销售量y(瓶)与销售单价x(元/瓶)之间满足一次函数关系,部分数据记录如表所示:
x(元/瓶) 22 24 26 27
y(瓶) 90 80 70 65
(1)直接写出y与x之间的函数关系式;(不需要写自变量x的取值范围)
(2)若该药店每天想从这批消毒洗手液的销售中获利325元,又想尽量给顾客实惠,问这批消毒洗手液每瓶的售价为多少元?
(3)该药店上级主管部门规定,消毒洗手液的每瓶利润不允许高于进价的,设这种消毒洗手液每天的总利润为w元,那么售价定为多少元时该药店可获得的利润最大?最大利润是多少元?
3.如图某桥拱截面可视为抛物线的一部分,在某一时刻,桥拱内的水面宽,桥拱顶点到水面的距离是.
(1)按如图所示的坐标系,求该桥拱的函数表达式;
(2)要保证高米的小船能够通过此桥(船顶与桥拱的距离不小于米),求小船的最大宽度是多少?
(3)如图,桥拱所在的函数图象的抛物线的轴下方部分与桥拱在平静水面中的倒影组成一个新函数图象.现将新函数图象向右平移()个单位长度,使得平移后的函数图象在之间,且随的增大而减小,请直接写出的取值范围.
4.为鼓励大学毕业生自主创业,某市政府出台了相关政策;由政府协调,本而企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.小柳按照政策投资销售本市生产的一种网红螺蛳粉.已知这种网红螺蛳粉的成本价为每箱80元,出厂价为每箱100元,每月销售量(箱)与销售单价(元)之间满足函数关系:.
(1)小柳在开始销售的第1月将螺蛳粉的销售单价定为120元,这个月他销售该螺蛳粉可获利________元.
(2)设小柳销售螺蛳粉获得的月利润为(元),当销售单价为多少元时,月利润最大,最大利润是多少元?
(3)物价部门规定,这种网红螺蛳粉的销售单价不得高于150元,那么政府每个月为他承担的总差价最少为多少元?
5.界首市公安交警部门提醒市民,骑车出行必须严格遵守“一盔一带”的规定.某头盔经销商统计了某品牌头盔4月份到6月份的销量,该品牌头盔4月份销售150个,6月份销售216个,且从4月份到6月份销售量的月增长率相同.
(1)求该品牌头盔销售量的月增长率;
(2)若此种头盔的进价为30元/个,经测算在市场中,当售价为40元/个时,月销售量为600个,若在此基础上售价每上涨1元,则月销售量将减少10个.
①为使月销售利润达到10000元,而且尽可能让顾客得到实惠,则该品牌头盔的实际售价应定为多少元/个 .
②要使销售该品牌头盔每月获得的利润最大,则该品牌头盔每个的售价为 元
6.学校要建一个矩形花圃,其中一边靠墙,另外三边用篱笆围成.已知墙长42m,篱笆长.设垂直于墙的边长为米,平行于墙的边为米,围成的矩形面积为.
(1)求与与的关系式.
(2)围成的矩形花圃面积能否为,若能,求出的值.
(3)围成的矩形花圃面积是否存在最大值?若存在,求出这个最大值,并求出此时的值.
7.某公司销售一种产品,经分析发现月销售量y(万件)与月份x(月)的关系如下表所示,每件产品的利润z(元)与月份x(月)满足关系式(,且x为整数).
x 1 2 3 4 5 6 7 8 9 10 11 12
y 28 32 36 40 44 48 52 52 52 52 52 52
(1)请你根据表格分别求出当和(x为整数)时,销售量y(万件)与月份x(月)的关系式;
(2)求当x为何值时,月利润(万元)有最大值,最大值为多少
(3)求该公司月利润不少于660万元的月份是哪几个月
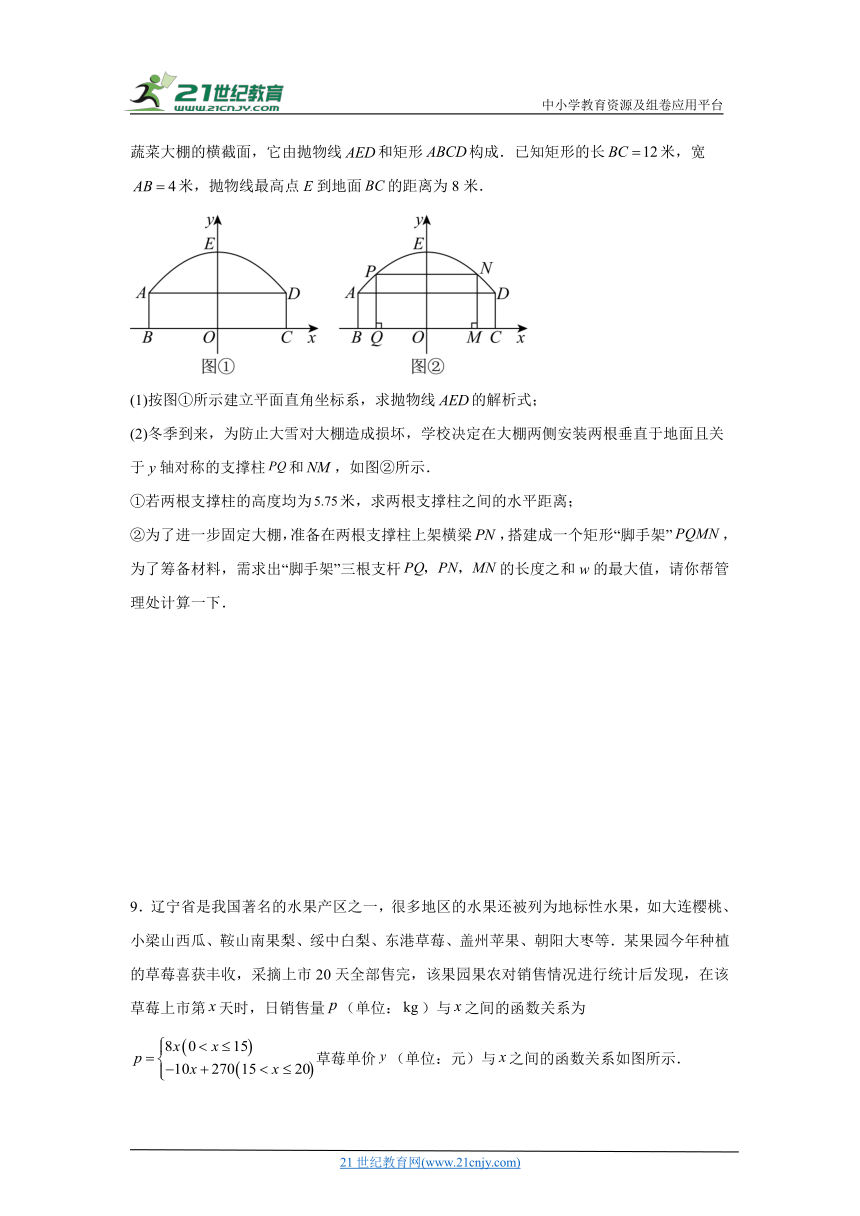
8.为培养学生劳动实践能力,某学校在校西南角开辟出一块劳动实践基地.如图①是其中蔬菜大棚的横截面,它由抛物线和矩形构成.已知矩形的长米,宽米,抛物线最高点E到地面的距离为8米.
(1)按图①所示建立平面直角坐标系,求抛物线的解析式;
(2)冬季到来,为防止大雪对大棚造成损坏,学校决定在大棚两侧安装两根垂直于地面且关于y轴对称的支撑柱和,如图②所示.
①若两根支撑柱的高度均为米,求两根支撑柱之间的水平距离;
②为了进一步固定大棚,准备在两根支撑柱上架横梁,搭建成一个矩形“脚手架”,为了筹备材料,需求出“脚手架”三根支杆的长度之和w的最大值,请你帮管理处计算一下.
9.辽宁省是我国著名的水果产区之一,很多地区的水果还被列为地标性水果,如大连樱桃、小梁山西瓜、鞍山南果梨、绥中白梨、东港草莓、盖州苹果、朝阳大枣等.某果园今年种植的草莓喜获丰收,采摘上市20天全部售完,该果园果农对销售情况进行统计后发现,在该草莓上市第天时,日销售量(单位:)与之间的函数关系为草莓单价(单位:元)与之间的函数关系如图所示.
(1)求第18天的日销售量;
(2)当时,求与之间的函数关系式;
(3)设日销售额为元,当时,求的最大值.
10.学校图书馆计划购进A、B两种图书共计200本,其中A种图书m本(m为整数),且A种图书的数量不超过B种图书的.根据调查,A、B两种图书原价分别为15元/本、20元/本,且有如下优惠方式:购买A种图书的单价 (元/本)关于购买数量x的函数关系为(且x为整数),若购买数量超过64本,则所购全部图书的单价与购买64本时的单价相同;购买B种图书的单价 (元/本)关于购买数量x的函数关系为(且x为整数),若购买数量超过100本,则所购全部图书单价与购买100本时的单价相同.
(1)若购买B种图书100本,则单价为 元/本;
(2)求m的取值范围;
(3)设图书馆购进A、B两种图书共支出w元,则A种图书购买数量m为多少时,支出费用w最低?最低费用为多少?
11.小明不仅是一名羽毛球运动爱好者,还喜欢运用数学知识对羽毛球比赛进行技术分析,下面是他对击球线路的分析,如图,在平面直角坐标系中,点A在x轴上,球网与y轴的水平距离,点C在点A的右侧,,击球点P在y轴上,若选择扣球,羽毛球的飞行高度y(m)与水平距离x(m)近似满足一次函数关系;若选择吊球,羽毛球的飞行高度y(m)与水平距离x(m)近似满足二次函数关系.
(1)求点P的坐标和a的值;
(2)小明分析发现,上面两种击球方式均能使球过网.要使球的落地点到点C的距离更近,请通过计算判断应该选择哪种击球方式;
(3)小明发现选择吊球更容易赢得比赛,所以重新设计抛物线,此时羽毛球的飞行高度y(m)与水平距离x(m)近似满足二次函数关系(),当时,y的最大值为4,求b的值.
12.某文具店最近有、两款纪念册比较畅销.款纪念册每本的进价为元,款纪念册每本的进价为元.在销售中发现:款纪念册售价为元本时,每天的销售量为本,每降低元可多售出本;款纪念册售价为元本时,每天的销售量为本,款纪念册每天的销售量与售价之间满足一次函数关系,其部分对应数据如下表所示:
售价(元/本) … …
每天销售量(本) … …
该店准备降低每本款纪念册的利润,同时提高每本款纪念册的利润,且这两款纪念册每天销售总数不变,设款纪念册每本降价元.
(1)直接写出款纪念册每天的销售量(用含的代数式表示);
(2)求出款纪念册每天的销售单价(用含的代数式表示);
(3)当款纪念册售价为多少元时,该店每天所获利润最大,最大利润是多少?
13.小明妈妈商店经销一种商品,根据以往的经验,每年进入了4月,这种商品需求量就会增大,妈妈让小明帮忙制定一个销售方案,小明查阅去年妈妈销售这种商品的记录,发现:该商品的进价为每件20元,去年3月份售价为每件30元.4月1日至19日每天在前一天的基础上涨价1元,4月20日至30日价格稳定在每件50元.3月31日销售这种商品160件,以后每天比上一天减少4件.设进入4月的第x天销售该商品的销售量为p,利润为y元.(每天利润=每天销售量×单件利润)
(1)分别求出p与x的函数关系式及y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于2400元?
14.2024年4月23日上午,山东青岛市莱西姜山工业园一企业厂房突发大火,导致该月我市某工业产品价格呈上升趋势,其前四周每周的平均销售价格变化如下表:
周数x
价格y(元/千克)
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接写出月份与的函数关系式;
(2)进入月,由于进口工业产品的上市,此种工业产品的平均销售价格(元千克)从月第周的元千克下降至第周的元千克,且与周数的变化情况满足二次函数,请求出月份与的函数关系式
(3)若月份此种工业产品的进价(元千克)与周数所满足的函数关系为,月份此种工业产品的进价(元千克)与周数所满足的函数关系为.试问月份与月份分别在哪一周销售此种工业产品一千克的利润最大?且最大利润分别是多少?
15.网络直播销售已经成为一种热门的销售方式,某生产商在一销售平台上进行直播销售板栗.已知板栗的成本价为6元/ ,每日销售量y()与销售单价x(元/ )满足一次函数关系,下表记录的是有关数据,经销售发现,销售单价不低于成本价且不高于元/ .设公司销售板栗的日获利为w(元).
x(元/ ) 7 8 9
y()
(1)直接写出日销售量y与销售单价x之间的函数关系式为______;(不用写自变量的取值范围)
(2)当销售单价定为多少时,销售这种板栗日获利w最大?最大利润为多少元?
(3)当销售单价在什么范围内时,日获利w不低于元?
16.为了振兴乡村经济,增加村民收入,某村委会干部带领村民在网上直播推销农产品,在试销售的30天中,第x天(且x为整数)的售价p(元/千克)与x的函数关系式(且x为整数),销量q(千克)与x的函数关系式为,已知第5天售价为50元/千克,第10天售价为40元/千克,设第x天的销售额为W元.
(1)______,______;
(2)求销售额W元与x之间的函数关系式,并求第x天时,销售额W最大;
(3)在试销售的30天中,销售额超过1000元的共有______天.
17.端午节快到了,光明企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该企业招收了新工人,设新工人李芹第x天生产的粽子数量为y只,y与x满足关系式.
如图,设第x天每只粽子的成本是p元,p与x之间的关系可用图中的函数图象来刻画.
(1)直接写出p与x之间的函数表达式;
(2)若李芹第x天创造的利润为w元.
①求w与x之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价-成本)
②设第m天利润达到最大值,若要使第天的利润比第m天的利润至少多72元,则第天每只粽子至少应提价几元?
18.保康县2024年大力推广一种成本为10元/斤的农产品,该产品售价不低于15元/斤,不高于30元/斤.
(1)每日销售量y(斤)与售价x(元/斤)之间满足如图函数关系式,求y与x之间的函数关系式;
(2)若每日销售利润为w(元),当售价定为多少时,每天销售利润最大?最大利润是多少?
(3)县科技助农队帮助果农降低种植成本,成本每斤减少m元,已知每日最大利润为2592元,求m的值.
19.九年级数学兴趣小组经过市场调查,整理出某种商品在第(且为整数)天的售价与销售量的相关信息如下表:
时间(天)
售价(元件)
每天销售量(件)
已知该商品的进价为每件元.请根据上面信息解答下面问题:
(1)销售该商品第几天时,当天销售利润为元?
(2)销售该商品第几天时,当天销售利润最大?最大利润是多少?
20.某商品每件进价25元,在试销阶段该商品的日销售量y(件)与每件商品的日销售价x(元)之间的关系如图中的折线所示(物价局规定,该商品每件的销售价不得低于进价且不得高于50元).
(1)直接写出y与x的函数关系式;
(2)若日销售单价x(元)为整数,则当日销售单价x(元)为多少时,该商品每天的销售利润最大?最大利润是多少;
(3)若该商品每天的销售利润不低于1200元,求销售单价x的取值范围.
21.随着家用小轿车的普及,交通安全已经成为千家万户关注的焦点,保持安全车距是预防交通事故的关键.已知某型号汽车刹车时速度为米秒,设刹车后行驶的时间为秒,刹车后速度为米秒,刹车后行驶的距离为米.已测得刹车后的运动速度与运动时间之间满足关系式:.刹车后行驶的距离与的函数图像如下图所示,该图像是抛物线,为常数,的一部分.
(1)当该汽车刹车后速度为米秒时,求刹车后行驶的时间.
(2)求、的值,以及该汽车刹车后行驶的最大距离.
(3)一司机驾驶该型号汽车,在以米秒的速度行驶中,突然发现导航提示前面米处路面变窄,于是立即刹车.为确保安全通过窄路,需要将车速降低到米秒以下.请通过计算说明该司机能否在到达窄路时将车速降低到米秒以下?
22.天气渐热,某商家购进一种冰镇饮料,每瓶进价是4元,并规定每瓶售价不得少于6元,日销售量不低于40瓶,根据以往销售经验发现,当每瓶售价定为6元时,日销售量为60瓶,每瓶售价每提高1元,日销售量减少5瓶,设每瓶售价为x元,日销售量为p瓶.
(1)当时,______;
(2)当每瓶售价定为多少元时,日销售利润w(元)最大?最大利润是多少?
(3)判断命题:“日销售额最大时,日销售利润不是最大”是______命题(填“真”或“假”),并说明理由.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.(1)
(2)每瓶洗手液的定价应为元或元
(3)当每瓶洗手液的售价定为元时,超市销售该品牌洗手液每天销售利润最大,最大利润是元
【分析】(1)设与之间的函数关系式为,利用待定系数法求解析式即可;
(2)根据销售数量乘以每千克的利润等于总利润列方程求解即可;
(3)设每天的销售利润为元,列函数关系式,根据二次函数的性质解答.
本题考查了一次函数的应用,二次函数的应用,一元二次方程的应用,正确理解题意是解题的关键.
【详解】(1)设与之间的函数关系式为,根据题意,得:
,
解得,
与之间的函数关系式为;
(2),
解得,,
,
,,
答:每瓶洗手液的定价应为元或元.
(3)设每天的销售利润为元,则有:
,
,
开口向下,
当时,随的增大而增大,
,且为整数.
当时,有最大值,最大值为元.
答:当每瓶洗手液的售价定为元时,超市销售该品牌洗手液每天销售利润最大,最大利润是元.
2.(1)与之间的函数关系式为
(2)这批消毒洗手液每瓶的售价为27元
(3)售价定为31元时该药店可获得的利润最大,最大利润是405元
【分析】本题主要考查了求一次函数的表达式,一元二次方程的实际应用,二次函数的实际应用,解题的关键是熟练掌握用待定系数法求解函数表达式的方法,根据题意找出等量关系,正确列出利润的表达式.
(1)设与之间的函数关系式为,将表格中的数据代入求解即可;
(2)根据总利润=单个利润×数量,列出方程求解即可,
(3)根据题意,列出总利润的函数表达式,化为顶点式,再根据每瓶利润不允许高于进价的确定自变量的取值,即可求解.
【详解】(1)解:设与之间的函数关系式为,
将时,和时代入得,
,
解得:,
∴与之间的函数关系式为.
(2)由(1)可知,每瓶售价为x元,每天销售量为y瓶,
,
∵,
∴,
整理得:,
解得:,,
∵尽量给顾客实惠,
∴.
答:这批消毒洗手液每瓶的售价为27元.
(3)
,
∵每瓶利润不允许高于进价的,
∴,
解得:,
∴当时,总利润为最大,此时(元).
∴售价定为31元时该药店可获得的利润最大,最大利润是405元.
3.(1)
(2)小船的最大宽度为米
(3)或
【分析】(1)先求出顶点的坐标,再根据待定系数法求解即可得解;
(2)二次函数的表达式中,令得,求解该方程即可得解;
(3)根据平移规律得到点平移后的对应点为,对称轴平移后的对称轴为,点平移后的对应点为,从而得或上,满足随的增大而减小,解不等式组即可得解.
【详解】(1)解:∵,且点在轴上,
∴,
根据抛物线的特点确定抛物线的对称轴为直线,
∴点,
设抛物线的解析式为,把原点代入得
,
解得,
∴此二次函数的表达式.
(2)解:∵二次函数的表达式,
∴令得:
,
解得:,,
∴小船的最大宽度为:米.
(3)解:根据平移规律得到点平移后的对应点为,对称轴平移后的对称轴为,点平移后的对应点为,根据图像性质,得到函数在或上,满足随的增大而减小,
∴或,
解得或,
故的取值范围是或.
【点睛】本题考查了抛物线的解析式,抛物线的平移,函数的增减性,解不等式组,抛物线的应用,熟练掌握抛物线的平移,函数的增减性,抛物线的应用是解题的关键.
4.(1)6400
(2)140元;最大利润7200元
(3)最少2000元
【分析】本题主要考查了一次函数与二次函数的综合应用,解题的关键是理清“成本价”、“出厂价”、“销售价”、“利润”之间的关系.
(1)先算出销售量,然后再算出获利多少元.注意:利润=销售量(销售价-成本价)
(2)根据题意列出月利润的二次函数关系式,整理成顶点式,可求得最大值.
(3)从销售单价的限额范围入手,表示出销售量的范围,最后再表示出政府承担的总差价即可得到结论.
【详解】(1)解:销售单价时,销售量,
共获利:(元),
故答案为:.
(2)设销售单价为x元时,月利润最大,
根据题意得: ,
当时,w值最大,最大值为7200,
答:销售单价为140元时,月利润最大,最大利润是7200元.
(3)依据题意知,销售单价,则销售量,
∴政府每个月为他承担的总差价:
答:那么政府每个月为他承担的总差价最少为2000元.
5.(1)该品牌头盔销售量的月增长率为
(2)①该品牌头盔的实际售价应定为50元;②65
【分析】(1)设该品牌头盔销售量的月增长率为,根据“从4月份到6月份销售量的月增长率相同”列一元二次方程,求解即可;
(2)①设该品牌头盔的实际售价为a元/个,根据月销售利润每个头盔的利润月销售量,即可得出关于a的一元二次方程,解之即可求出答案.
②设该品牌头盔每月获得的利润为y元,则,根据二次函数的性质即可求解.
【详解】(1)解:设该品牌头盔销售量的月增长率为x,
根据题意可得,,
解得,(舍去),
答:该品牌头盔销售量的月增长率为;
(2)解:①设该品牌头盔的实际售价应定为a元,
由题意得,
整理得,
解得,,
∵尽可能让顾客得到实惠,
∴,
∴该品牌头盔的实际售价应定为50元.
②设该品牌头盔每月获得的利润为y元,则
,
,抛物线开口向下,
∴当时,y有最大值,最大值为12250.
∴该品牌头盔每个的售价为65元.
故答案为:65
【点睛】本题考查了列一元二次方程解决增长率问题和利润问题,以及根据二次函数的性质求最大值问题.找出等量关系且熟练掌握解一元二次方程是解题的关键.
6.(1);
(2)能,
(3)的最大值为800,此时
【分析】本题主要考查一元二次方程的应用和二次函数的实际应用:
(1)根据可求出与之间的关系,根据墙的长度可确定的范围;根据面积公式可确立二次函数关系式;
(2)令,得一元二次方程,判断此方程有解,再解方程即可 ;
(3)根据自变量的取值范围和二次函数的性质确定函数的最大值即可.
【详解】(1)解:∵篱笆长,
∴,
∵
∴
∴
∵墙长42m,
∴,
解得,,
∴;
又矩形面积
;
(2)解:令,则,
整理得:,
此时,,
所以,一元二次方程有两个不相等的实数根,
∴围成的矩形花圃面积能为;
∴
∴
∵,
∴;
(3)解:
∵
∴有最大值,
又,
∴当时,取得最大值,此时,
即当时,的最大值为800
7.(1)(,x为整数),(,x为整数)
(2)当,月利润(万元)有最大值,最大值为676万元
(3)5,6,7月
【分析】(1)当时,设,用待定系数法求解即可,而当时,不变,且为52,因此;
(2)当,为整数时,,转化为二次函数求最值问题即可;当,为整数时,,根据一次函数的性质即可求解,最后再比较最大值即可;
(3)当,为整数时,令,解得,结合函数图像得到当,为整数时,月利润不少于660万元,当,为整数时,,故可得月利润不少于660万元的月份是5,6,7月.
【详解】(1)解:根据表格可知,当时,设,
当,,
则,
解得:,
∴,
当时,,
综上可得:(,x为整数),(,x为整数);
(2)解:当,为整数时,,
∵,且对称轴为直线,
∴随着x的增大而增大,
∴当,月利润(万元)有最大值,最大值为676万元;
当,为整数时,,
∵,
∴当,随着x的增大而减小,
∴当时,有最大值,元,
综上可得:当,月利润(万元)有最大值,最大值为676万元;
(3)解:当,为整数时,则,
化简得:,
令,
当时,即,
解得,
∴结合如下图像:当时,
得,而,
∴当,为整数时,月利润不少于660万元,
当,为整数时,,
综上所述,月利润不少于660万元的月份是5,6,7月.
【点睛】本题考查了一次函数与二次函数的实际应用,待定系数法求一次函数解析式,一次函数的性质,二次函数的最值,二次函数图像与不等式的关系,熟练掌握知识点,正确理解题意是解题的关键.
8.(1)抛物线的解析式为:
(2)①两根支撑柱之间的水平距离为9米;②“脚手架”三根支杆的长度之和w的最大值为米.
【分析】本题主要考查了待定系数法求二次函数的解析式、二次函数的性质、求二次函数的最值等知识点,熟练掌握待定系数法求二次函数的解析式是解题的关键.
(1)由题意得、、,设抛物线的解析式为,将代入解析式求得a即可解答;
(2)①根据题意可得,解方程即可得到,从而即可算出两根支撑柱之间的水平距离;②设N点坐标为,则,,进而得到,然后根据二次函数的性质求最值即可.
【详解】(1)解:∵四边形是矩形,
∴(米),,
∴点,点,
根据题意和图象可得,顶点E的坐标为,
∴可设抛物线的解析式为:,
把点代入解析式可得:,解得:,
∴抛物线的解析式为:.
(2)解:①当时,,解得,
(米),
∴两根支撑柱之间的水平距离为9米;
②设N点坐标为,则,,
∴,
∵,,
∴当时,w有最大值,最大值为,
∴“脚手架”三根支杆的长度之和w的最大值为米.
9.(1)第18天的日销售量为
(2)
(3)的最大值为1560
【分析】本题主要考查了一次函数和二次函数的应用,解题的关键是理解题意,熟练掌握待定系数法.
(1)把代入求出结果即可;
(2)用待定系数法求出与之间的函数关系式即可;
(3)分两种情况:当时,当时,分别求出的最大值,然后进行判断即可.
【详解】(1)解:当时,,
∴第18天的日销售量为.
(2)解:当时,设与之间的函数关系式为,
将点,代入,得,
解得,
∴与之间的函数关系式为.
(3)解:当时,,
∵,随的增大而增大,
∴当时,取得最大值,最大值为.
当时,
,
∵,
∴当时,随的增大而增大,
∴当时,取得最大值,最大值为:
.
∵,
∴当时,的最大值为1560.
10.(1)10
(2) (m为整数)
(3)m为50时,支出费用w最低,w最低费用为1937.5元
【分析】本题主要考查二次函数的实际应用、一次函数的实际应用、不等式的实际应用能力,根据题意准确抓住相等关系或不等关系是解题的根本和关键.
(1)将代入中求解,即可解题;
(2)根据问题是实际意义,以及“A种图书的数量不超过B种图书的”建立不等式求解,即可解题;
(3)根据题意列出支出费用w关于的表达式,再根据二次函数的图象与性质求解,即可解题.
【详解】(1)解:,
当时,,
购买B种图书100本,则单价为元/本;
故答案为:.
(2)解:由题知,A种图书m本(m为整数),则B种图书本,
A种图书的数量不超过B种图书的.
,
解得,
m的取值范围是 (m为整数);
(3)解:由题知,,
,
,
,
,,
当m为50时,支出费用w最低,w最低费用为元.
11.(1),;
(2)应选择吊球;
(3).
【分析】本题考查了二次函数的实际应用;
(1)依据题意,对于一次函数,令,可求得y值,即为P点坐标,将P点坐标代入二次函数中,可解得a的值,即可求解;
(2)依据题意,分别计算一次函数、二次函数与x轴的交点,比较两点到C点的距离,可得选择哪种击球方式使球的落地点到点C的距离更近,即可求解;
(3)依据题意,由,又,从而当时,y随x的增大而增大;当时,y随x的增大而减小,再由,进而根据二次函数的性质进行分类讨论①当时,②当时,③当时,即可求解.
理解、表示的实际意义,掌握待定系数法及二次函数的性质,能根据二次函数的性质进行分类讨论是解题的关键.
【详解】(1)解:由题意得,
对于一次函数,
令,则,
,
将P点坐标代入二次函数中,
,
.
(2)解:由题意得,
对于一次函数,
令,
,
解得:,
对于二次函数,
令,(),
,
,,
,
,
应选择吊球.
(3)解:由题意得
,
当时,,
当时,,
当时,,
,
当时,y随x的增大而增大;
当时,y随x的增大而减小.
①当时,
,
当时,y最大,即,
;
②当时,
,
当时,y最大,
即,
,
故此时无解;
③当时,
,
当时,y最大,
即.
,
此时不合题意.
综上所述:.
12.(1)
(2)
(3)当款纪念册售价为元时,该店每天所获利润最大,最大利润是元
【分析】本题考查一次函数及二次函数的应用;
(1)设A款纪念册每本降价元,根据这两款纪念册每天销售总数不变,则款纪念册销售量为本;
(2)设款纪念册每天的销售量与售价之间满足的一次函数关系是,根据表格得出一次函数关系式,即可求解;
(3)设该店每天所获利润是元.根据每周的利润每本的利润每周的销售数量,再根据二次函数的性质可得答案.
【详解】(1)设款纪念册每本降价元,
则款纪念册销售量为本,售价为元,则每册利润为(元),
这两款纪念册每天销售总数不变,
款纪念册销售量为本;
(2)设款纪念册每天的销售量与售价之间满足的一次函数关系是.
根据表格,可得,
解得.
所以.
当时,,即款纪念册每天的销售量为本时,每本售价是元.
(3)设该店每天所获利润是元.
由题意,得.
因为,所以当时,取最大值,最大值为元.
此时款纪念册售价为(元)
答:当款纪念册售价为元时,该店每天所获利润最大,最大利润是元.
13.(1);
(2)第15天时,当天的销售利润最大,最大利润为2500元.
(3)11天
【分析】本题主要考查二次函数、一次函数的应用能力:
(1)根据题意写出p与x的函数关系式及y与x的函数关系式即可;
(2)分和求出相应的函数解析式,求出各自最大利润值,然后再比较可得结论;
(3)令,可得前19天中有10天每天销售利润不低于2400元,后11天中,只有1天达到2400元,故可得结论
【详解】(1)解:,
当时,,
当时,,
综上:;
(2)解:当时,,
∵,
∴当时,y有最大值,最大值为2500元.
当时,,
∵,
∴y随x的增大而减小,
∴当时,y有最大值,最大值为2400元,
综上可知,当时,当天的销售利润最大,最大利润为2500元;
(3)解:令,
解得,(,舍去),
∴前19天中有10天每天销售利润不低于2400元,后11天中,只有1天达到2400元,
∴共有11天每天销售利润不低于2400元.
答:共有11天每天销售利润不低于2400元.
14.(1)
(2)
(3)月份在第一周的工业产品一千克的利润最大,最大利润为0.55元;月份在第一周的工业产品一千克的利润最大,最大利润为1元
【分析】本题考查了一次函数,二次函数解析式求法及二次函数的实际应用.
(1)从表格看出,x每增加1,y就增加0.2,由此可确定是一次函数关系式,继而代入两点可得出解析式;
(2)将代入,可求b,c的值,确定二次函数解析式;
(3)根据一次函数,二次函数的性质及自变量的取值范围,求最大利润
【详解】(1)解:通过观察可知,每增加一周,价格增加0.2元,
∴四月份周数y与x 的符合一次函数关系式,
设这个关系式为:,
则,
解得:,
∴4月份y与x 的函数关系式为;
(2)将代入.
可得:
解得:
即;
(3)4月份此种工业产品利润可表示为:,即: ;
由函数解析式可知,四月份的利润随周数的增大而减小,所以应在第一周的利润最大,最大为:(元/千克),
5月份此种工业产品利润可表示为:,
即:,
由函数解析式可知,五月份的利润随周数变化符合二次函数且对称轴为: ,
即在第1至4周的利润随周数的增大而减小,
所以应在第一周的利润最大,最大为:(元/千克).
15.(1)
(2)当销售单价定为元时,日获利w最大,最大利润为元
(3)
【分析】(1)设日销售量y与销售单价x之间的函数关系式,将,,代入得,,计算求解,进而可得结果;
(2)依题意得,,由,,可知当时,日获利w最大,最大利润为元;
(3)令,则,可求或,由,可得,由,可得.
【详解】(1)解:设日销售量y与销售单价x之间的函数关系式,
将,,代入得,,
解得,,
∴日销售量y与销售单价x之间的函数关系式;
(2)解:依题意得,,
∵,,
∴当时,日获利w最大,最大利润为元;
(3)解:令,则,
解得,或,
∵,
∴,
又∵,
∴.
【点睛】本题考查了一次函数的应用,二次函数的应用,二次函数的图象与性质,二次函数与一元二次方程的关系等知识.熟练掌握一次函数的应用,二次函数的应用,二次函数的图象与性质,二次函数与一元二次方程的关系是解题的关键.
16.(1);60
(2);第30天时,销售额W最大
(3)7
【分析】本题考查一次函数和二次函数的应用,解题的关键是读懂题意,列出函数关系式.
(1)用待定系数法可得,的值;
(2)由销售额,分两种情况可得函数关系式,再分别 根据函数值比较即可得答案;
(3)分两种情况,结合(2)可列出方程解得答案.
【详解】(1)解:把,代入得:
,
解得,
故答案为:,60;
(2)解:由(1)可得,
当时,;
当时,;
;
当,,
∵,
∴当时,W有最大值,最大值为800;
当时,,
∵,
∴W随x增大而增大,
∴时,W有最大值,最大值为,
∵,
∴第30天时,销售额W最大.
(3)解:在中,令得:,
整理得,
方程无实数解;
由得,
整数,
可取24,25,26,27,28,29,30,
销售额超过1000元的共有7天.
17.(1)当时,;当时,
(2)①当时,w有最大值,最大值为864元;②第9天每只粽子至少应提价0.2元
【分析】本题考查的是二次函数在实际生活中的应用,主要考查了利用二次函数的增减性求最值问题,利用一次函数的增减性求最值等知识点,
(1)由图象知当时,,当时,利用待定系数法即可得解;
(2)①分和)两种情况讨论即可得解;②设第9天提价a元,由题意得列出不等式,解不等式即可得解;
读懂题目信息,列出相关的函数关系式是解题关键.
【详解】(1)由图象得,当时,;
当时,图象是一条直线,经过,,
∴可设直线解析式为,
∴,
∴,
∴,
∴p与x之间的函数表达式为:;
(2)①(Ⅰ)若,则,
∴当时,(元);
(Ⅱ)若,,
,
∴当时,(元);
综上,当时,w有最大值,最大值为864元;
②由①可知,,
设第9天提价a元,由题意得,,
,解得,
答:第9天每只粽子至少应提价元.
18.(1)
(2)当售价定为25时,每天销售利润最大,最大利润是1800元
(3)
【分析】本题考查了一次函数及二次函数的应用,待定系数法求函数解析式,利用函数解决实际问题时,要注意自变量的取值范围,这也是解决实际问题的难点和关键
(1)由图象可知函数为一次函数,设函数关系式为,待定系数法求出函数解析式即可;
(2)设每日销售利润为w元,根据x的取值范围,利用二次函数模型即可求出最大利润;
(3)设成本每斤减少m元后每日销售利润为Q元,由和确定当时,利润最大,从而得出关于的方程,解出方程即可求得m值.
【详解】(1)解:由图象可知函数为一次函数,设函数关系式为,
当时,,当时,,
,解得:,
与x之间的函数关系式为;
(2)根据题意得:,
,
,
抛物线开口方向向下,
对称轴,,
当时,利润最大,
元;
(3)设成本每斤减少m后每日销售利润为Q元,
则,
抛物线对称轴为,
,
,
,
当时,利润最大,
,
解得:,(不合题意舍去),
答:m的值为6.
19.(1)销售该商品第天或第天时,当天销售利润为元
(2)销售该商品第天时,当天销售利润最大,最大利润是元
【分析】()分和两种情况列出方程解答即可求解;
()分和两种情况列出与之间的函数关系式,再根据函数的性质解答即可求解;
本题考查了二元一次方程的应用,一元一次方程的应用,二次函数和一次函数的应用,根据题意,正确列出方程和函数解析式是解题的关键.
【详解】(1)解:当时,,
整理得,,
解得,(不合,舍去),
∴;
当时,,
解得;
答:销售该商品第天或第天时,当天销售利润为元;
(2)解:当时,
,
∵,,
∴当时,当天销售利润最大,元;
当时,,
∵,,
∴当时,当天销售利润最大,;
∵,
∴销售该商品第天时,当天销售利润最大,最大利润是元.
20.(1)
(2)当日销售单价为42元或43元时,每天的销售利润最大,最大利润为1224元
(3)
【分析】本题考查一次函数的实际应用,二次函数的实际应用,从图象中有效的获取信息,正确的求出函数解析式是解题的关键:
(1)分2段,待定系数法求出函数解析式即可;
(2)设销售利润为W元,根据总利润等于单件利润乘以销量列出函数关系式,利用二次函数的性质,求最值即可;
(3)根据该商品每天的销售利润不低于1200元,列出不等式,利用图象法解不等式即可.
【详解】(1)设段的解析式为:,
由图可知:图象经过,
则:,解得:,
∴;
设段的解析式为:,
由图可知:图象经过,
则:,解得:,
∴
∴.
(2)设销售利润为W元,则
①当时,,
∴时,元.
②当时,,
∵x为整数,
∴或43时,W取最大值,.
∵,
∴当日销售单价为42元或43元时,每天的销售利润最大,最大利润为1224元.
(3)由(2)知,当时,该商品每天的最大销售利润为1000元;
∴只有在时,每天的销售利润才可能不低于1200元;
∴,
当,解得:,
∵,
∴的解集为.
21.(1)秒
(2),,米
(3)能
【分析】本题考查了一次函数与二次函数的应用;
(1)把代入,即可求解;
(2)待定系数法求解析式,即可求解;
(3)把代入得,,当时,求得,即可求解.
【详解】(1)把代入,
得,解得
(2)把,代入得
解得
因为
当时,最大,最大值为
即,,刹车后行驶的最大距离为米.
(3)由题意:把代入得,
一,解得
当时,
所以,该司机到达窄路时可将车速降低到米秒以下.
22.(1)50
(2)当每瓶售价时,日销售量最大,最大利润为240元
(3)真,详见解析
【分析】本题考查了二次函数的实际应用,解决问题的关键是弄清题意,列出函数解析式并求出x的取值范围.
(1)根据每瓶售价每提高1元,日销售量减少5瓶,当时,售价提高2元,则日销售量减少10瓶,即可得出结论;
(2)根据每瓶利润×日销售量=总利润,可得w关于x的关系式,再根据题意求出自变量的取值范围,由二次函数性质可得答案;
(3)设日销售额为y元,根据日销售额=销售单价×销售量列出函数解析式,根据函数的性质求出y取最大值时x的值,再求出此时的利润即可判断.
【详解】(1)解:,
故答案为:50;
(2)由题意可得,,
则,
∵每瓶售价不得少于6元,日销售量不低于40瓶,
∴,
解得,
∵,
∴当时,w有最大值,最大利润为240,
答:当每瓶售价定为10元时,日销售利润w(元)最大,最大利润是240元;
(3)设日销售额为y元,
则,
∵,,
∴当时,日销售额y有最大值为405元,
而此时日销售利润w为225元,不是最大,
所以原命题是真命题,
故答案为:真.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
人教版九年级上册数学第二十二章二次函数应用题训练
1.超市销售某品牌洗手液,进价为每瓶元在销售过程中发现,每天销售量瓶与每瓶售价元之间满足一次函数关系其中,且为整数,当每瓶洗手液的售价是元时,每天销售量为瓶;当每瓶洗手液的售价是元时,每天销售量为瓶.
(1)求与之间的函数关系式;
(2)超市要想使该品牌洗手液的销售利润平均每天达到元,每瓶洗手液的定价应为多少元?
(3)设超市销售该品牌洗手液每天销售利润为元,当每瓶洗手液的售价定为多少元时,超市销售该品牌洗手液每天销售利润最大,最大利润是多少元?
2.消毒洗手液与百姓生活息息相关,某药店的消毒洗手液很畅销.已知该消毒洗手液的进价为每瓶22元,经市场调查,每天洗手液的销售量y(瓶)与销售单价x(元/瓶)之间满足一次函数关系,部分数据记录如表所示:
x(元/瓶) 22 24 26 27
y(瓶) 90 80 70 65
(1)直接写出y与x之间的函数关系式;(不需要写自变量x的取值范围)
(2)若该药店每天想从这批消毒洗手液的销售中获利325元,又想尽量给顾客实惠,问这批消毒洗手液每瓶的售价为多少元?
(3)该药店上级主管部门规定,消毒洗手液的每瓶利润不允许高于进价的,设这种消毒洗手液每天的总利润为w元,那么售价定为多少元时该药店可获得的利润最大?最大利润是多少元?
3.如图某桥拱截面可视为抛物线的一部分,在某一时刻,桥拱内的水面宽,桥拱顶点到水面的距离是.
(1)按如图所示的坐标系,求该桥拱的函数表达式;
(2)要保证高米的小船能够通过此桥(船顶与桥拱的距离不小于米),求小船的最大宽度是多少?
(3)如图,桥拱所在的函数图象的抛物线的轴下方部分与桥拱在平静水面中的倒影组成一个新函数图象.现将新函数图象向右平移()个单位长度,使得平移后的函数图象在之间,且随的增大而减小,请直接写出的取值范围.
4.为鼓励大学毕业生自主创业,某市政府出台了相关政策;由政府协调,本而企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.小柳按照政策投资销售本市生产的一种网红螺蛳粉.已知这种网红螺蛳粉的成本价为每箱80元,出厂价为每箱100元,每月销售量(箱)与销售单价(元)之间满足函数关系:.
(1)小柳在开始销售的第1月将螺蛳粉的销售单价定为120元,这个月他销售该螺蛳粉可获利________元.
(2)设小柳销售螺蛳粉获得的月利润为(元),当销售单价为多少元时,月利润最大,最大利润是多少元?
(3)物价部门规定,这种网红螺蛳粉的销售单价不得高于150元,那么政府每个月为他承担的总差价最少为多少元?
5.界首市公安交警部门提醒市民,骑车出行必须严格遵守“一盔一带”的规定.某头盔经销商统计了某品牌头盔4月份到6月份的销量,该品牌头盔4月份销售150个,6月份销售216个,且从4月份到6月份销售量的月增长率相同.
(1)求该品牌头盔销售量的月增长率;
(2)若此种头盔的进价为30元/个,经测算在市场中,当售价为40元/个时,月销售量为600个,若在此基础上售价每上涨1元,则月销售量将减少10个.
①为使月销售利润达到10000元,而且尽可能让顾客得到实惠,则该品牌头盔的实际售价应定为多少元/个 .
②要使销售该品牌头盔每月获得的利润最大,则该品牌头盔每个的售价为 元
6.学校要建一个矩形花圃,其中一边靠墙,另外三边用篱笆围成.已知墙长42m,篱笆长.设垂直于墙的边长为米,平行于墙的边为米,围成的矩形面积为.
(1)求与与的关系式.
(2)围成的矩形花圃面积能否为,若能,求出的值.
(3)围成的矩形花圃面积是否存在最大值?若存在,求出这个最大值,并求出此时的值.
7.某公司销售一种产品,经分析发现月销售量y(万件)与月份x(月)的关系如下表所示,每件产品的利润z(元)与月份x(月)满足关系式(,且x为整数).
x 1 2 3 4 5 6 7 8 9 10 11 12
y 28 32 36 40 44 48 52 52 52 52 52 52
(1)请你根据表格分别求出当和(x为整数)时,销售量y(万件)与月份x(月)的关系式;
(2)求当x为何值时,月利润(万元)有最大值,最大值为多少
(3)求该公司月利润不少于660万元的月份是哪几个月
8.为培养学生劳动实践能力,某学校在校西南角开辟出一块劳动实践基地.如图①是其中蔬菜大棚的横截面,它由抛物线和矩形构成.已知矩形的长米,宽米,抛物线最高点E到地面的距离为8米.
(1)按图①所示建立平面直角坐标系,求抛物线的解析式;
(2)冬季到来,为防止大雪对大棚造成损坏,学校决定在大棚两侧安装两根垂直于地面且关于y轴对称的支撑柱和,如图②所示.
①若两根支撑柱的高度均为米,求两根支撑柱之间的水平距离;
②为了进一步固定大棚,准备在两根支撑柱上架横梁,搭建成一个矩形“脚手架”,为了筹备材料,需求出“脚手架”三根支杆的长度之和w的最大值,请你帮管理处计算一下.
9.辽宁省是我国著名的水果产区之一,很多地区的水果还被列为地标性水果,如大连樱桃、小梁山西瓜、鞍山南果梨、绥中白梨、东港草莓、盖州苹果、朝阳大枣等.某果园今年种植的草莓喜获丰收,采摘上市20天全部售完,该果园果农对销售情况进行统计后发现,在该草莓上市第天时,日销售量(单位:)与之间的函数关系为草莓单价(单位:元)与之间的函数关系如图所示.
(1)求第18天的日销售量;
(2)当时,求与之间的函数关系式;
(3)设日销售额为元,当时,求的最大值.
10.学校图书馆计划购进A、B两种图书共计200本,其中A种图书m本(m为整数),且A种图书的数量不超过B种图书的.根据调查,A、B两种图书原价分别为15元/本、20元/本,且有如下优惠方式:购买A种图书的单价 (元/本)关于购买数量x的函数关系为(且x为整数),若购买数量超过64本,则所购全部图书的单价与购买64本时的单价相同;购买B种图书的单价 (元/本)关于购买数量x的函数关系为(且x为整数),若购买数量超过100本,则所购全部图书单价与购买100本时的单价相同.
(1)若购买B种图书100本,则单价为 元/本;
(2)求m的取值范围;
(3)设图书馆购进A、B两种图书共支出w元,则A种图书购买数量m为多少时,支出费用w最低?最低费用为多少?
11.小明不仅是一名羽毛球运动爱好者,还喜欢运用数学知识对羽毛球比赛进行技术分析,下面是他对击球线路的分析,如图,在平面直角坐标系中,点A在x轴上,球网与y轴的水平距离,点C在点A的右侧,,击球点P在y轴上,若选择扣球,羽毛球的飞行高度y(m)与水平距离x(m)近似满足一次函数关系;若选择吊球,羽毛球的飞行高度y(m)与水平距离x(m)近似满足二次函数关系.
(1)求点P的坐标和a的值;
(2)小明分析发现,上面两种击球方式均能使球过网.要使球的落地点到点C的距离更近,请通过计算判断应该选择哪种击球方式;
(3)小明发现选择吊球更容易赢得比赛,所以重新设计抛物线,此时羽毛球的飞行高度y(m)与水平距离x(m)近似满足二次函数关系(),当时,y的最大值为4,求b的值.
12.某文具店最近有、两款纪念册比较畅销.款纪念册每本的进价为元,款纪念册每本的进价为元.在销售中发现:款纪念册售价为元本时,每天的销售量为本,每降低元可多售出本;款纪念册售价为元本时,每天的销售量为本,款纪念册每天的销售量与售价之间满足一次函数关系,其部分对应数据如下表所示:
售价(元/本) … …
每天销售量(本) … …
该店准备降低每本款纪念册的利润,同时提高每本款纪念册的利润,且这两款纪念册每天销售总数不变,设款纪念册每本降价元.
(1)直接写出款纪念册每天的销售量(用含的代数式表示);
(2)求出款纪念册每天的销售单价(用含的代数式表示);
(3)当款纪念册售价为多少元时,该店每天所获利润最大,最大利润是多少?
13.小明妈妈商店经销一种商品,根据以往的经验,每年进入了4月,这种商品需求量就会增大,妈妈让小明帮忙制定一个销售方案,小明查阅去年妈妈销售这种商品的记录,发现:该商品的进价为每件20元,去年3月份售价为每件30元.4月1日至19日每天在前一天的基础上涨价1元,4月20日至30日价格稳定在每件50元.3月31日销售这种商品160件,以后每天比上一天减少4件.设进入4月的第x天销售该商品的销售量为p,利润为y元.(每天利润=每天销售量×单件利润)
(1)分别求出p与x的函数关系式及y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于2400元?
14.2024年4月23日上午,山东青岛市莱西姜山工业园一企业厂房突发大火,导致该月我市某工业产品价格呈上升趋势,其前四周每周的平均销售价格变化如下表:
周数x
价格y(元/千克)
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接写出月份与的函数关系式;
(2)进入月,由于进口工业产品的上市,此种工业产品的平均销售价格(元千克)从月第周的元千克下降至第周的元千克,且与周数的变化情况满足二次函数,请求出月份与的函数关系式
(3)若月份此种工业产品的进价(元千克)与周数所满足的函数关系为,月份此种工业产品的进价(元千克)与周数所满足的函数关系为.试问月份与月份分别在哪一周销售此种工业产品一千克的利润最大?且最大利润分别是多少?
15.网络直播销售已经成为一种热门的销售方式,某生产商在一销售平台上进行直播销售板栗.已知板栗的成本价为6元/ ,每日销售量y()与销售单价x(元/ )满足一次函数关系,下表记录的是有关数据,经销售发现,销售单价不低于成本价且不高于元/ .设公司销售板栗的日获利为w(元).
x(元/ ) 7 8 9
y()
(1)直接写出日销售量y与销售单价x之间的函数关系式为______;(不用写自变量的取值范围)
(2)当销售单价定为多少时,销售这种板栗日获利w最大?最大利润为多少元?
(3)当销售单价在什么范围内时,日获利w不低于元?
16.为了振兴乡村经济,增加村民收入,某村委会干部带领村民在网上直播推销农产品,在试销售的30天中,第x天(且x为整数)的售价p(元/千克)与x的函数关系式(且x为整数),销量q(千克)与x的函数关系式为,已知第5天售价为50元/千克,第10天售价为40元/千克,设第x天的销售额为W元.
(1)______,______;
(2)求销售额W元与x之间的函数关系式,并求第x天时,销售额W最大;
(3)在试销售的30天中,销售额超过1000元的共有______天.
17.端午节快到了,光明企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该企业招收了新工人,设新工人李芹第x天生产的粽子数量为y只,y与x满足关系式.
如图,设第x天每只粽子的成本是p元,p与x之间的关系可用图中的函数图象来刻画.
(1)直接写出p与x之间的函数表达式;
(2)若李芹第x天创造的利润为w元.
①求w与x之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价-成本)
②设第m天利润达到最大值,若要使第天的利润比第m天的利润至少多72元,则第天每只粽子至少应提价几元?
18.保康县2024年大力推广一种成本为10元/斤的农产品,该产品售价不低于15元/斤,不高于30元/斤.
(1)每日销售量y(斤)与售价x(元/斤)之间满足如图函数关系式,求y与x之间的函数关系式;
(2)若每日销售利润为w(元),当售价定为多少时,每天销售利润最大?最大利润是多少?
(3)县科技助农队帮助果农降低种植成本,成本每斤减少m元,已知每日最大利润为2592元,求m的值.
19.九年级数学兴趣小组经过市场调查,整理出某种商品在第(且为整数)天的售价与销售量的相关信息如下表:
时间(天)
售价(元件)
每天销售量(件)
已知该商品的进价为每件元.请根据上面信息解答下面问题:
(1)销售该商品第几天时,当天销售利润为元?
(2)销售该商品第几天时,当天销售利润最大?最大利润是多少?
20.某商品每件进价25元,在试销阶段该商品的日销售量y(件)与每件商品的日销售价x(元)之间的关系如图中的折线所示(物价局规定,该商品每件的销售价不得低于进价且不得高于50元).
(1)直接写出y与x的函数关系式;
(2)若日销售单价x(元)为整数,则当日销售单价x(元)为多少时,该商品每天的销售利润最大?最大利润是多少;
(3)若该商品每天的销售利润不低于1200元,求销售单价x的取值范围.
21.随着家用小轿车的普及,交通安全已经成为千家万户关注的焦点,保持安全车距是预防交通事故的关键.已知某型号汽车刹车时速度为米秒,设刹车后行驶的时间为秒,刹车后速度为米秒,刹车后行驶的距离为米.已测得刹车后的运动速度与运动时间之间满足关系式:.刹车后行驶的距离与的函数图像如下图所示,该图像是抛物线,为常数,的一部分.
(1)当该汽车刹车后速度为米秒时,求刹车后行驶的时间.
(2)求、的值,以及该汽车刹车后行驶的最大距离.
(3)一司机驾驶该型号汽车,在以米秒的速度行驶中,突然发现导航提示前面米处路面变窄,于是立即刹车.为确保安全通过窄路,需要将车速降低到米秒以下.请通过计算说明该司机能否在到达窄路时将车速降低到米秒以下?
22.天气渐热,某商家购进一种冰镇饮料,每瓶进价是4元,并规定每瓶售价不得少于6元,日销售量不低于40瓶,根据以往销售经验发现,当每瓶售价定为6元时,日销售量为60瓶,每瓶售价每提高1元,日销售量减少5瓶,设每瓶售价为x元,日销售量为p瓶.
(1)当时,______;
(2)当每瓶售价定为多少元时,日销售利润w(元)最大?最大利润是多少?
(3)判断命题:“日销售额最大时,日销售利润不是最大”是______命题(填“真”或“假”),并说明理由.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.(1)
(2)每瓶洗手液的定价应为元或元
(3)当每瓶洗手液的售价定为元时,超市销售该品牌洗手液每天销售利润最大,最大利润是元
【分析】(1)设与之间的函数关系式为,利用待定系数法求解析式即可;
(2)根据销售数量乘以每千克的利润等于总利润列方程求解即可;
(3)设每天的销售利润为元,列函数关系式,根据二次函数的性质解答.
本题考查了一次函数的应用,二次函数的应用,一元二次方程的应用,正确理解题意是解题的关键.
【详解】(1)设与之间的函数关系式为,根据题意,得:
,
解得,
与之间的函数关系式为;
(2),
解得,,
,
,,
答:每瓶洗手液的定价应为元或元.
(3)设每天的销售利润为元,则有:
,
,
开口向下,
当时,随的增大而增大,
,且为整数.
当时,有最大值,最大值为元.
答:当每瓶洗手液的售价定为元时,超市销售该品牌洗手液每天销售利润最大,最大利润是元.
2.(1)与之间的函数关系式为
(2)这批消毒洗手液每瓶的售价为27元
(3)售价定为31元时该药店可获得的利润最大,最大利润是405元
【分析】本题主要考查了求一次函数的表达式,一元二次方程的实际应用,二次函数的实际应用,解题的关键是熟练掌握用待定系数法求解函数表达式的方法,根据题意找出等量关系,正确列出利润的表达式.
(1)设与之间的函数关系式为,将表格中的数据代入求解即可;
(2)根据总利润=单个利润×数量,列出方程求解即可,
(3)根据题意,列出总利润的函数表达式,化为顶点式,再根据每瓶利润不允许高于进价的确定自变量的取值,即可求解.
【详解】(1)解:设与之间的函数关系式为,
将时,和时代入得,
,
解得:,
∴与之间的函数关系式为.
(2)由(1)可知,每瓶售价为x元,每天销售量为y瓶,
,
∵,
∴,
整理得:,
解得:,,
∵尽量给顾客实惠,
∴.
答:这批消毒洗手液每瓶的售价为27元.
(3)
,
∵每瓶利润不允许高于进价的,
∴,
解得:,
∴当时,总利润为最大,此时(元).
∴售价定为31元时该药店可获得的利润最大,最大利润是405元.
3.(1)
(2)小船的最大宽度为米
(3)或
【分析】(1)先求出顶点的坐标,再根据待定系数法求解即可得解;
(2)二次函数的表达式中,令得,求解该方程即可得解;
(3)根据平移规律得到点平移后的对应点为,对称轴平移后的对称轴为,点平移后的对应点为,从而得或上,满足随的增大而减小,解不等式组即可得解.
【详解】(1)解:∵,且点在轴上,
∴,
根据抛物线的特点确定抛物线的对称轴为直线,
∴点,
设抛物线的解析式为,把原点代入得
,
解得,
∴此二次函数的表达式.
(2)解:∵二次函数的表达式,
∴令得:
,
解得:,,
∴小船的最大宽度为:米.
(3)解:根据平移规律得到点平移后的对应点为,对称轴平移后的对称轴为,点平移后的对应点为,根据图像性质,得到函数在或上,满足随的增大而减小,
∴或,
解得或,
故的取值范围是或.
【点睛】本题考查了抛物线的解析式,抛物线的平移,函数的增减性,解不等式组,抛物线的应用,熟练掌握抛物线的平移,函数的增减性,抛物线的应用是解题的关键.
4.(1)6400
(2)140元;最大利润7200元
(3)最少2000元
【分析】本题主要考查了一次函数与二次函数的综合应用,解题的关键是理清“成本价”、“出厂价”、“销售价”、“利润”之间的关系.
(1)先算出销售量,然后再算出获利多少元.注意:利润=销售量(销售价-成本价)
(2)根据题意列出月利润的二次函数关系式,整理成顶点式,可求得最大值.
(3)从销售单价的限额范围入手,表示出销售量的范围,最后再表示出政府承担的总差价即可得到结论.
【详解】(1)解:销售单价时,销售量,
共获利:(元),
故答案为:.
(2)设销售单价为x元时,月利润最大,
根据题意得: ,
当时,w值最大,最大值为7200,
答:销售单价为140元时,月利润最大,最大利润是7200元.
(3)依据题意知,销售单价,则销售量,
∴政府每个月为他承担的总差价:
答:那么政府每个月为他承担的总差价最少为2000元.
5.(1)该品牌头盔销售量的月增长率为
(2)①该品牌头盔的实际售价应定为50元;②65
【分析】(1)设该品牌头盔销售量的月增长率为,根据“从4月份到6月份销售量的月增长率相同”列一元二次方程,求解即可;
(2)①设该品牌头盔的实际售价为a元/个,根据月销售利润每个头盔的利润月销售量,即可得出关于a的一元二次方程,解之即可求出答案.
②设该品牌头盔每月获得的利润为y元,则,根据二次函数的性质即可求解.
【详解】(1)解:设该品牌头盔销售量的月增长率为x,
根据题意可得,,
解得,(舍去),
答:该品牌头盔销售量的月增长率为;
(2)解:①设该品牌头盔的实际售价应定为a元,
由题意得,
整理得,
解得,,
∵尽可能让顾客得到实惠,
∴,
∴该品牌头盔的实际售价应定为50元.
②设该品牌头盔每月获得的利润为y元,则
,
,抛物线开口向下,
∴当时,y有最大值,最大值为12250.
∴该品牌头盔每个的售价为65元.
故答案为:65
【点睛】本题考查了列一元二次方程解决增长率问题和利润问题,以及根据二次函数的性质求最大值问题.找出等量关系且熟练掌握解一元二次方程是解题的关键.
6.(1);
(2)能,
(3)的最大值为800,此时
【分析】本题主要考查一元二次方程的应用和二次函数的实际应用:
(1)根据可求出与之间的关系,根据墙的长度可确定的范围;根据面积公式可确立二次函数关系式;
(2)令,得一元二次方程,判断此方程有解,再解方程即可 ;
(3)根据自变量的取值范围和二次函数的性质确定函数的最大值即可.
【详解】(1)解:∵篱笆长,
∴,
∵
∴
∴
∵墙长42m,
∴,
解得,,
∴;
又矩形面积
;
(2)解:令,则,
整理得:,
此时,,
所以,一元二次方程有两个不相等的实数根,
∴围成的矩形花圃面积能为;
∴
∴
∵,
∴;
(3)解:
∵
∴有最大值,
又,
∴当时,取得最大值,此时,
即当时,的最大值为800
7.(1)(,x为整数),(,x为整数)
(2)当,月利润(万元)有最大值,最大值为676万元
(3)5,6,7月
【分析】(1)当时,设,用待定系数法求解即可,而当时,不变,且为52,因此;
(2)当,为整数时,,转化为二次函数求最值问题即可;当,为整数时,,根据一次函数的性质即可求解,最后再比较最大值即可;
(3)当,为整数时,令,解得,结合函数图像得到当,为整数时,月利润不少于660万元,当,为整数时,,故可得月利润不少于660万元的月份是5,6,7月.
【详解】(1)解:根据表格可知,当时,设,
当,,
则,
解得:,
∴,
当时,,
综上可得:(,x为整数),(,x为整数);
(2)解:当,为整数时,,
∵,且对称轴为直线,
∴随着x的增大而增大,
∴当,月利润(万元)有最大值,最大值为676万元;
当,为整数时,,
∵,
∴当,随着x的增大而减小,
∴当时,有最大值,元,
综上可得:当,月利润(万元)有最大值,最大值为676万元;
(3)解:当,为整数时,则,
化简得:,
令,
当时,即,
解得,
∴结合如下图像:当时,
得,而,
∴当,为整数时,月利润不少于660万元,
当,为整数时,,
综上所述,月利润不少于660万元的月份是5,6,7月.
【点睛】本题考查了一次函数与二次函数的实际应用,待定系数法求一次函数解析式,一次函数的性质,二次函数的最值,二次函数图像与不等式的关系,熟练掌握知识点,正确理解题意是解题的关键.
8.(1)抛物线的解析式为:
(2)①两根支撑柱之间的水平距离为9米;②“脚手架”三根支杆的长度之和w的最大值为米.
【分析】本题主要考查了待定系数法求二次函数的解析式、二次函数的性质、求二次函数的最值等知识点,熟练掌握待定系数法求二次函数的解析式是解题的关键.
(1)由题意得、、,设抛物线的解析式为,将代入解析式求得a即可解答;
(2)①根据题意可得,解方程即可得到,从而即可算出两根支撑柱之间的水平距离;②设N点坐标为,则,,进而得到,然后根据二次函数的性质求最值即可.
【详解】(1)解:∵四边形是矩形,
∴(米),,
∴点,点,
根据题意和图象可得,顶点E的坐标为,
∴可设抛物线的解析式为:,
把点代入解析式可得:,解得:,
∴抛物线的解析式为:.
(2)解:①当时,,解得,
(米),
∴两根支撑柱之间的水平距离为9米;
②设N点坐标为,则,,
∴,
∵,,
∴当时,w有最大值,最大值为,
∴“脚手架”三根支杆的长度之和w的最大值为米.
9.(1)第18天的日销售量为
(2)
(3)的最大值为1560
【分析】本题主要考查了一次函数和二次函数的应用,解题的关键是理解题意,熟练掌握待定系数法.
(1)把代入求出结果即可;
(2)用待定系数法求出与之间的函数关系式即可;
(3)分两种情况:当时,当时,分别求出的最大值,然后进行判断即可.
【详解】(1)解:当时,,
∴第18天的日销售量为.
(2)解:当时,设与之间的函数关系式为,
将点,代入,得,
解得,
∴与之间的函数关系式为.
(3)解:当时,,
∵,随的增大而增大,
∴当时,取得最大值,最大值为.
当时,
,
∵,
∴当时,随的增大而增大,
∴当时,取得最大值,最大值为:
.
∵,
∴当时,的最大值为1560.
10.(1)10
(2) (m为整数)
(3)m为50时,支出费用w最低,w最低费用为1937.5元
【分析】本题主要考查二次函数的实际应用、一次函数的实际应用、不等式的实际应用能力,根据题意准确抓住相等关系或不等关系是解题的根本和关键.
(1)将代入中求解,即可解题;
(2)根据问题是实际意义,以及“A种图书的数量不超过B种图书的”建立不等式求解,即可解题;
(3)根据题意列出支出费用w关于的表达式,再根据二次函数的图象与性质求解,即可解题.
【详解】(1)解:,
当时,,
购买B种图书100本,则单价为元/本;
故答案为:.
(2)解:由题知,A种图书m本(m为整数),则B种图书本,
A种图书的数量不超过B种图书的.
,
解得,
m的取值范围是 (m为整数);
(3)解:由题知,,
,
,
,
,,
当m为50时,支出费用w最低,w最低费用为元.
11.(1),;
(2)应选择吊球;
(3).
【分析】本题考查了二次函数的实际应用;
(1)依据题意,对于一次函数,令,可求得y值,即为P点坐标,将P点坐标代入二次函数中,可解得a的值,即可求解;
(2)依据题意,分别计算一次函数、二次函数与x轴的交点,比较两点到C点的距离,可得选择哪种击球方式使球的落地点到点C的距离更近,即可求解;
(3)依据题意,由,又,从而当时,y随x的增大而增大;当时,y随x的增大而减小,再由,进而根据二次函数的性质进行分类讨论①当时,②当时,③当时,即可求解.
理解、表示的实际意义,掌握待定系数法及二次函数的性质,能根据二次函数的性质进行分类讨论是解题的关键.
【详解】(1)解:由题意得,
对于一次函数,
令,则,
,
将P点坐标代入二次函数中,
,
.
(2)解:由题意得,
对于一次函数,
令,
,
解得:,
对于二次函数,
令,(),
,
,,
,
,
应选择吊球.
(3)解:由题意得
,
当时,,
当时,,
当时,,
,
当时,y随x的增大而增大;
当时,y随x的增大而减小.
①当时,
,
当时,y最大,即,
;
②当时,
,
当时,y最大,
即,
,
故此时无解;
③当时,
,
当时,y最大,
即.
,
此时不合题意.
综上所述:.
12.(1)
(2)
(3)当款纪念册售价为元时,该店每天所获利润最大,最大利润是元
【分析】本题考查一次函数及二次函数的应用;
(1)设A款纪念册每本降价元,根据这两款纪念册每天销售总数不变,则款纪念册销售量为本;
(2)设款纪念册每天的销售量与售价之间满足的一次函数关系是,根据表格得出一次函数关系式,即可求解;
(3)设该店每天所获利润是元.根据每周的利润每本的利润每周的销售数量,再根据二次函数的性质可得答案.
【详解】(1)设款纪念册每本降价元,
则款纪念册销售量为本,售价为元,则每册利润为(元),
这两款纪念册每天销售总数不变,
款纪念册销售量为本;
(2)设款纪念册每天的销售量与售价之间满足的一次函数关系是.
根据表格,可得,
解得.
所以.
当时,,即款纪念册每天的销售量为本时,每本售价是元.
(3)设该店每天所获利润是元.
由题意,得.
因为,所以当时,取最大值,最大值为元.
此时款纪念册售价为(元)
答:当款纪念册售价为元时,该店每天所获利润最大,最大利润是元.
13.(1);
(2)第15天时,当天的销售利润最大,最大利润为2500元.
(3)11天
【分析】本题主要考查二次函数、一次函数的应用能力:
(1)根据题意写出p与x的函数关系式及y与x的函数关系式即可;
(2)分和求出相应的函数解析式,求出各自最大利润值,然后再比较可得结论;
(3)令,可得前19天中有10天每天销售利润不低于2400元,后11天中,只有1天达到2400元,故可得结论
【详解】(1)解:,
当时,,
当时,,
综上:;
(2)解:当时,,
∵,
∴当时,y有最大值,最大值为2500元.
当时,,
∵,
∴y随x的增大而减小,
∴当时,y有最大值,最大值为2400元,
综上可知,当时,当天的销售利润最大,最大利润为2500元;
(3)解:令,
解得,(,舍去),
∴前19天中有10天每天销售利润不低于2400元,后11天中,只有1天达到2400元,
∴共有11天每天销售利润不低于2400元.
答:共有11天每天销售利润不低于2400元.
14.(1)
(2)
(3)月份在第一周的工业产品一千克的利润最大,最大利润为0.55元;月份在第一周的工业产品一千克的利润最大,最大利润为1元
【分析】本题考查了一次函数,二次函数解析式求法及二次函数的实际应用.
(1)从表格看出,x每增加1,y就增加0.2,由此可确定是一次函数关系式,继而代入两点可得出解析式;
(2)将代入,可求b,c的值,确定二次函数解析式;
(3)根据一次函数,二次函数的性质及自变量的取值范围,求最大利润
【详解】(1)解:通过观察可知,每增加一周,价格增加0.2元,
∴四月份周数y与x 的符合一次函数关系式,
设这个关系式为:,
则,
解得:,
∴4月份y与x 的函数关系式为;
(2)将代入.
可得:
解得:
即;
(3)4月份此种工业产品利润可表示为:,即: ;
由函数解析式可知,四月份的利润随周数的增大而减小,所以应在第一周的利润最大,最大为:(元/千克),
5月份此种工业产品利润可表示为:,
即:,
由函数解析式可知,五月份的利润随周数变化符合二次函数且对称轴为: ,
即在第1至4周的利润随周数的增大而减小,
所以应在第一周的利润最大,最大为:(元/千克).
15.(1)
(2)当销售单价定为元时,日获利w最大,最大利润为元
(3)
【分析】(1)设日销售量y与销售单价x之间的函数关系式,将,,代入得,,计算求解,进而可得结果;
(2)依题意得,,由,,可知当时,日获利w最大,最大利润为元;
(3)令,则,可求或,由,可得,由,可得.
【详解】(1)解:设日销售量y与销售单价x之间的函数关系式,
将,,代入得,,
解得,,
∴日销售量y与销售单价x之间的函数关系式;
(2)解:依题意得,,
∵,,
∴当时,日获利w最大,最大利润为元;
(3)解:令,则,
解得,或,
∵,
∴,
又∵,
∴.
【点睛】本题考查了一次函数的应用,二次函数的应用,二次函数的图象与性质,二次函数与一元二次方程的关系等知识.熟练掌握一次函数的应用,二次函数的应用,二次函数的图象与性质,二次函数与一元二次方程的关系是解题的关键.
16.(1);60
(2);第30天时,销售额W最大
(3)7
【分析】本题考查一次函数和二次函数的应用,解题的关键是读懂题意,列出函数关系式.
(1)用待定系数法可得,的值;
(2)由销售额,分两种情况可得函数关系式,再分别 根据函数值比较即可得答案;
(3)分两种情况,结合(2)可列出方程解得答案.
【详解】(1)解:把,代入得:
,
解得,
故答案为:,60;
(2)解:由(1)可得,
当时,;
当时,;
;
当,,
∵,
∴当时,W有最大值,最大值为800;
当时,,
∵,
∴W随x增大而增大,
∴时,W有最大值,最大值为,
∵,
∴第30天时,销售额W最大.
(3)解:在中,令得:,
整理得,
方程无实数解;
由得,
整数,
可取24,25,26,27,28,29,30,
销售额超过1000元的共有7天.
17.(1)当时,;当时,
(2)①当时,w有最大值,最大值为864元;②第9天每只粽子至少应提价0.2元
【分析】本题考查的是二次函数在实际生活中的应用,主要考查了利用二次函数的增减性求最值问题,利用一次函数的增减性求最值等知识点,
(1)由图象知当时,,当时,利用待定系数法即可得解;
(2)①分和)两种情况讨论即可得解;②设第9天提价a元,由题意得列出不等式,解不等式即可得解;
读懂题目信息,列出相关的函数关系式是解题关键.
【详解】(1)由图象得,当时,;
当时,图象是一条直线,经过,,
∴可设直线解析式为,
∴,
∴,
∴,
∴p与x之间的函数表达式为:;
(2)①(Ⅰ)若,则,
∴当时,(元);
(Ⅱ)若,,
,
∴当时,(元);
综上,当时,w有最大值,最大值为864元;
②由①可知,,
设第9天提价a元,由题意得,,
,解得,
答:第9天每只粽子至少应提价元.
18.(1)
(2)当售价定为25时,每天销售利润最大,最大利润是1800元
(3)
【分析】本题考查了一次函数及二次函数的应用,待定系数法求函数解析式,利用函数解决实际问题时,要注意自变量的取值范围,这也是解决实际问题的难点和关键
(1)由图象可知函数为一次函数,设函数关系式为,待定系数法求出函数解析式即可;
(2)设每日销售利润为w元,根据x的取值范围,利用二次函数模型即可求出最大利润;
(3)设成本每斤减少m元后每日销售利润为Q元,由和确定当时,利润最大,从而得出关于的方程,解出方程即可求得m值.
【详解】(1)解:由图象可知函数为一次函数,设函数关系式为,
当时,,当时,,
,解得:,
与x之间的函数关系式为;
(2)根据题意得:,
,
,
抛物线开口方向向下,
对称轴,,
当时,利润最大,
元;
(3)设成本每斤减少m后每日销售利润为Q元,
则,
抛物线对称轴为,
,
,
,
当时,利润最大,
,
解得:,(不合题意舍去),
答:m的值为6.
19.(1)销售该商品第天或第天时,当天销售利润为元
(2)销售该商品第天时,当天销售利润最大,最大利润是元
【分析】()分和两种情况列出方程解答即可求解;
()分和两种情况列出与之间的函数关系式,再根据函数的性质解答即可求解;
本题考查了二元一次方程的应用,一元一次方程的应用,二次函数和一次函数的应用,根据题意,正确列出方程和函数解析式是解题的关键.
【详解】(1)解:当时,,
整理得,,
解得,(不合,舍去),
∴;
当时,,
解得;
答:销售该商品第天或第天时,当天销售利润为元;
(2)解:当时,
,
∵,,
∴当时,当天销售利润最大,元;
当时,,
∵,,
∴当时,当天销售利润最大,;
∵,
∴销售该商品第天时,当天销售利润最大,最大利润是元.
20.(1)
(2)当日销售单价为42元或43元时,每天的销售利润最大,最大利润为1224元
(3)
【分析】本题考查一次函数的实际应用,二次函数的实际应用,从图象中有效的获取信息,正确的求出函数解析式是解题的关键:
(1)分2段,待定系数法求出函数解析式即可;
(2)设销售利润为W元,根据总利润等于单件利润乘以销量列出函数关系式,利用二次函数的性质,求最值即可;
(3)根据该商品每天的销售利润不低于1200元,列出不等式,利用图象法解不等式即可.
【详解】(1)设段的解析式为:,
由图可知:图象经过,
则:,解得:,
∴;
设段的解析式为:,
由图可知:图象经过,
则:,解得:,
∴
∴.
(2)设销售利润为W元,则
①当时,,
∴时,元.
②当时,,
∵x为整数,
∴或43时,W取最大值,.
∵,
∴当日销售单价为42元或43元时,每天的销售利润最大,最大利润为1224元.
(3)由(2)知,当时,该商品每天的最大销售利润为1000元;
∴只有在时,每天的销售利润才可能不低于1200元;
∴,
当,解得:,
∵,
∴的解集为.
21.(1)秒
(2),,米
(3)能
【分析】本题考查了一次函数与二次函数的应用;
(1)把代入,即可求解;
(2)待定系数法求解析式,即可求解;
(3)把代入得,,当时,求得,即可求解.
【详解】(1)把代入,
得,解得
(2)把,代入得
解得
因为
当时,最大,最大值为
即,,刹车后行驶的最大距离为米.
(3)由题意:把代入得,
一,解得
当时,
所以,该司机到达窄路时可将车速降低到米秒以下.
22.(1)50
(2)当每瓶售价时,日销售量最大,最大利润为240元
(3)真,详见解析
【分析】本题考查了二次函数的实际应用,解决问题的关键是弄清题意,列出函数解析式并求出x的取值范围.
(1)根据每瓶售价每提高1元,日销售量减少5瓶,当时,售价提高2元,则日销售量减少10瓶,即可得出结论;
(2)根据每瓶利润×日销售量=总利润,可得w关于x的关系式,再根据题意求出自变量的取值范围,由二次函数性质可得答案;
(3)设日销售额为y元,根据日销售额=销售单价×销售量列出函数解析式,根据函数的性质求出y取最大值时x的值,再求出此时的利润即可判断.
【详解】(1)解:,
故答案为:50;
(2)由题意可得,,
则,
∵每瓶售价不得少于6元,日销售量不低于40瓶,
∴,
解得,
∵,
∴当时,w有最大值,最大利润为240,
答:当每瓶售价定为10元时,日销售利润w(元)最大,最大利润是240元;
(3)设日销售额为y元,
则,
∵,,
∴当时,日销售额y有最大值为405元,
而此时日销售利润w为225元,不是最大,
所以原命题是真命题,
故答案为:真.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
