九年级数学上点拨与训练 第二十一章 一元二次方程小结与复习 同步学案(含解析)
文档属性
| 名称 | 九年级数学上点拨与训练 第二十一章 一元二次方程小结与复习 同步学案(含解析) | 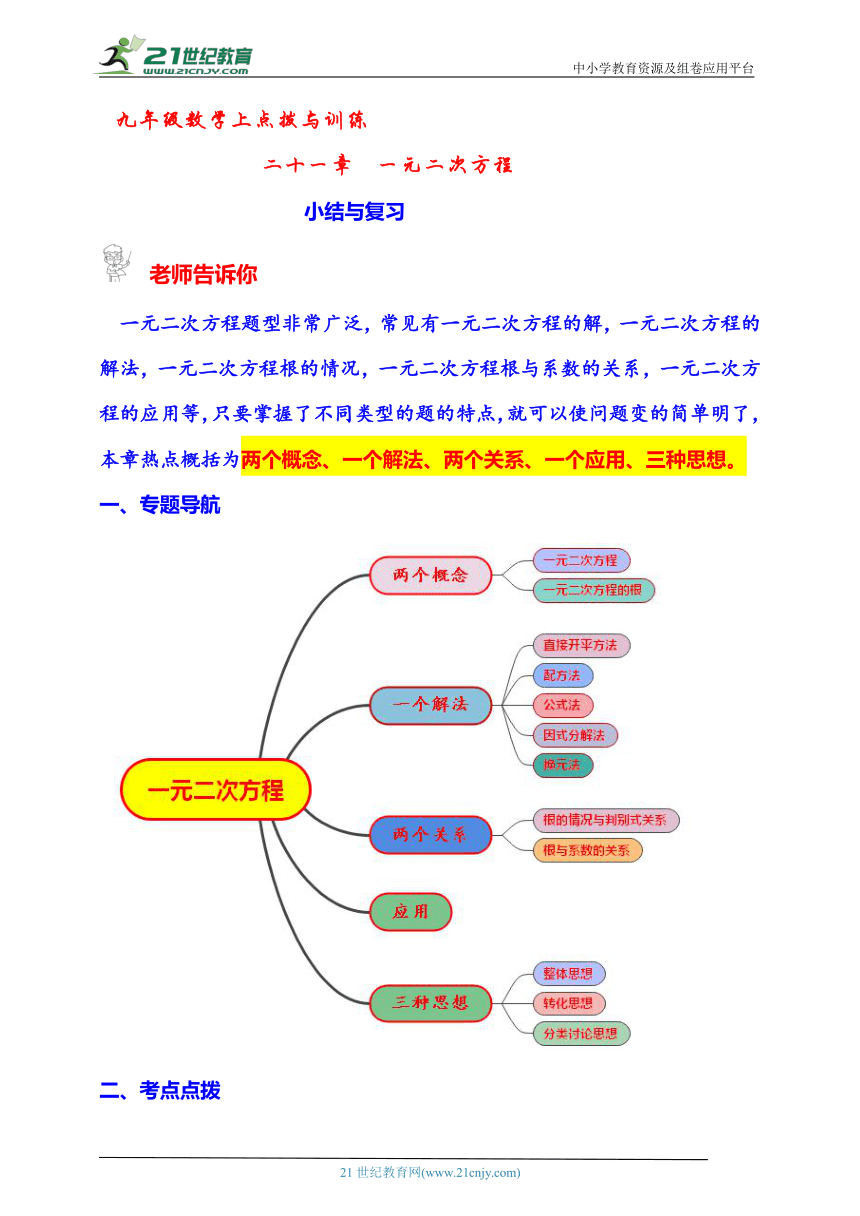 | |
| 格式 | doc | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-11 09:33:54 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
九年级数学上点拨与训练
二十一章 一元二次方程
小结与复习
老师告诉你
一元二次方程题型非常广泛,常见有一元二次方程的解,一元二次方程的解法,一元二次方程根的情况,一元二次方程根与系数的关系,一元二次方程的应用等,只要掌握了不同类型的题的特点,就可以使问题变的简单明了,本章热点概括为两个概念、一个解法、两个关系、一个应用、三种思想。
一、专题导航
二、考点点拨
考点1 两个概念
概念1一元二次方程的定义
典例剖析1
典例1.若方程是关于x的一元二次方程,则m的值为______________.
针对练习1
1.已知是关于x的一元二次方程,则___________.
2.若方程是关于x的一元二次方程,则m的值为( )
A.2 B.-2 C.2或-2 D.0
3.如果方程是关于x的一元二次方程,那么m的值为( )
A.±3 B.3 C.-3 D.都不对
概念2一元二次方程的根
典例剖析2
典例2.若关于x的一元二次方程有一个根是1,则m的值为( )
A.4 B.3 C.2 D.
针对练习2
1.已知关于x的一元二次方程.
(1)若.求证:必是该方程的一个根.
(2)当a,b,c之间的关系是_________时,方程必有一根是.
2.已知实数a是一元二次方程的一个根,求代数式的值.
3.若是关于x的方程的解,则的值为__________.
考点2 一个解法----一元二次方程的解法
典例剖析3
典例3.用适当的方法解下列方程.
(1);
(2);
(3).
针对练习3
1.解方程:
(1)(公式法);
(2)(配方法);
(3);
(4).
2.下面是小明解一元二次方程的过程,请认真阅读并完成相应的任务.
二次系数化为1,得………………………………第一步移项,得.……………………………………第二步配方,得,即……………………第三步由此,可得……………………………………第四步所以,,……………………第五步
任务:
(1)上面小明同学的解法中运用“配方法”将该一元二次方程“降次”为两个一元一次方程,体现的数学思想是,其中“配方法”所依据的一个数学公式是;
(2)“第二步”变形的依据是;
(3)上面小明同学解题过程中,从第____步开始出现错误,请直接写出正确的解;
(4)请你根据平时学习经验,就解一元二次方程时还需要注意的事项为其他同学提一条意见.
3.阅读下面的材料,回答问题:
要解方程,我们发现这是一个一元四次方程,不容易直接求解,如果注意到,根据该方程的特点,我们可以这样做:
解析:设,
那么,
于是原方程可变为,
解得,.
当时,,
;
当时,,
;
原方程有四个根,,,.
我们把以上这种解决问题的方法叫做换元法.
任务:
(1)上述解方程的过程体现的数学思想主要是( )
A.分类讨论思想 B.转化思想 C.数形结合思想 D.公理化思想
(2)仿照上面的方法,解方程;
(3)若实数m、n满足,则的值是__________.
考点3 两个关系
关系1一元二次方程的根与判别式的关系
典例剖析4
典例4.若关于x的一元二次方程有两个不相等的实数根,则k的取值范围是( )
A. B.,且 C.,且 D.
针对练习4
1.已知关于x的一元二次方程,其中m,n在数轴上对应的点如图所示,则这个方程的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
2.已知关于x的一元二次方程有两个相等的实数根,则的值等于( )
A.0 B.1 C.2 D.无法确定
3.关于x的一元二次方程有实根,则m的最大整数解是( )
A.2 B.3 C.4 D.5
4.已知关于x的一元二次方程,其中a、b、c分别为三边的长.
(1)如果是方程的根,试判断的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断的形状,并说明理由;
(3)如果是等边三角形,试求这个一元二次方程的根.
关系2一元二次方程根与系数的关系
典例剖析5
典例5.如果x、y是两个实数()且,,则的值等于( )
A. B. C. D.2023
针对练习5
1.若与是方程的两个实数根,则_________.
2.已知关于x的一元二次方程.
(1)求证:无论m取何值,该方程都有两个不相等的实数根.
(2)设方程的两个根分别为,,且,若,求m的值.
3.阅读材料:材料1 若一元二次方程的两根为、,则,
材料2:已知实数、满足、,且,求的值.
解:由题知、是方程的两个不相等的实数根,根据材料1得,
根据上述材料解决下面问题:
(1)一元二次方程的两根为、,则=_____,=_____.
(2)已知实数、满足、,且,求的值.
(3)已知实数、满足、,且,求的值.
4.已知,是一元二次方程的两个实数根.
(1)求k的取值范围;
(2)是否存在实数k,使得等式成立?如果存在,请求出k的值,如果不存在,请说明理由.
考点4 一个应用---一元二次方程的应用
典例剖析6
典例6.如图,老李想用长为的栅栏,再借助房屋的外墙(外墙足够长)围成一个矩形羊圈,并在边上留一个宽的门(建在处,另用其他材料).
(1)当羊圈的长和宽分别为多少米时,能围成一个面积为的羊圈?
(2)羊圈的面积能达到吗?如果能,请你给出设计方案;如果不能,请说明理由.
针对练习6
1.某商场销售一批衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,商场采取了降价措施.假设在一定范围内,衬衫的单价每降1元,商场平均每天可多售出2件.如果降价后商场销售这批衬衫每天盈利1250元,那么衬衫的单价降了多少元?
2.有一人患了流感,经过两轮传染后共有144人患了流感.
(1)求每轮传染中平均一个人传染了几个人.
(2)如果不及时控制,三轮传染后,患流感的有多少人?
.
3.某市计划举办青少年足球比赛,赛制采取双循环形式(即每两队之间都要打两场比赛),一共组织30场比赛.计分规则为胜一场得3分,平一场得1分,负一场得0分.
(1)该市举办方应该邀请多少支球队参赛?
(2)此次比赛结束后,如果其中一支参赛球队共平了4场,负了2场,则该球队此次比赛的总积分是多少?
4.甲、乙两个机器人分别从相距70米的A,B两个位置同时出发,相向运动.甲第1分钟走了2米,且以后每分钟比前1分钟多走1米,乙每分钟走5米.
(1)甲、乙开始运动多少分钟后第一次相遇?
(2)如果甲、乙到达B或A后立即折返,甲继续每分钟比前1分钟多走1米,乙继续按照每分钟5米的速度行走,那么它们开始运动多少分钟后第二次相遇?
考点5 三种思想
思想1 整体思想
典例剖析7
典例7.若α,β是方程x2+2x-2005=0的两个实数根,则α2+3α+β的值为( )
A. 2005 B. 2003 C. -2005 D. 4010
针对练习7
1.已知是方程的两个根,则的值为( )
A. 9 B. 10 C. 12 D. 15
2.已知m,n是一元二次方程x2+3x-6=0的两个根,则m2+mn+3m的值为( )
A. 0 B. 3 C. 6 D. 13
3.阅读材料,解答问题:
已知实数m,n满足m2-m-1=0,n2-n-1=0,且m≠n,则m,n是方程x2-x-1=0的两个不相等的实数根,由韦达定理可知m+n=1,mn=-1.
根据上述材料,解决以下问题:
(1)直接应用:
已知实数a,b满足:a2-7a+1=0,b2-7b+1=0且a≠b,则a+b=_____,ab=_____;
(2)间接应用:
在(1)的条件下,求的值;
(3)拓展应用:
已知实数m,n满足:,n2-n=7且mn≠-1,求的值.
4.阅读材料,解答问题:
材料1
为了解方程(x2)2-13x2+36=0,如果我们把x2看作一个整体,然后设y=x2,则原方程可化为y2-13y+36=0,经过运算,原方程的解为x1,2=±2,x3,4=±3.我们把以上这种解决问题的方法通常叫做换元法.
材料2
已知实数m,n满足m2-m-1=0,n2-n-1=0,且m≠n,显然m,n是方程x2-x-1=0的两个不相等的实数根,由韦达定理可知m+n=1,mn=-1.
根据上述材料,解决以下问题:
(1)直接应用:
方程x4-5x2+6=0的解为 _____;
(2)间接应用:
已知实数a,b满足:2a4-7a2+1=0,2b4-7b2+1=0且a≠b,求a4+b4的值;
(3)拓展应用:
已知实数m,n满足:+=7,n2-n=7且n>0,求+n2的值.
思想2 转化思想
典例剖析8
典例8.已知关于y的一元二次方程(m+1)y2-3my-9=0的根都是整数,且m满足等式,则满足条件的所有整数m的和是( )
A. -5 B. -4 C. 0 D. -6
针对练习8
1.一张桌子的桌面长为6m,宽为4m,台布面积是桌面面积的2倍,如果将台布铺在桌子上,各边垂下的长度相同.求这块台布的长和宽.
2.如图,在宽为20m,长为32m的矩形地上,修筑同样宽的三条道路,把耕地分成大小不等的六块,要使耕地面积为570m2,求道路的宽为多少米?
3.在北京2008年第29届奥运会前夕,某超市在销售中发现:奥运会吉祥物“福娃”平均每天可售出20套,每件盈利40元.为了迎接奥运会,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存,经市场调查发现:如果每套降价1元,那么平均每天就可多售出2套.要想平均每天在销售吉祥物上盈利1200元,那么每套应降价多少?
思想3 分类讨论思想
典例剖析9
典例9.定义:已知,是关于x的一元二次方程的两个实数根,若,且,则称这个方程为“限根方程”.如:一元二次方程的两根为,,因,,所以一元二次方程为“限根方程”.
请阅读以上材料,回答下列问题:
(1)判断一元二次方程是否为“限根方程”,并说明理由;
(2)若关于x的一元二次方程是“限根方程”,且两根、满足,求k的值;
(3)若关于x的一元二次方程是“限根方程”,求m的取值范围.
针对练习9
1.已知关于x的一元二次方程.
(1)求证:不论k取何值,方程总有两个不相等的实数根;
(2)若方程两根的和比两根的积大1,求k的值;
(3)若的两边a,b的长是这个方程的两个实数根,第三边c的长为2,当是等腰三角形时,求k的值.
2.已知关于x的方程.
(1)若是方程的一个根,求m的值和方程的另一根;
(2)当m为何实数时,方程有实数根;
(3)若,是方程的两个根,且,试求实数m的值.
九年级数学上点拨与训练
二十一章 一元二次方程
小结与复习
老师告诉你
一元二次方程题型非常广泛,常见有一元二次方程的解,一元二次方程的解法,一元二次方程根的情况,一元二次方程根与系数的关系,一元二次方程的应用等,只要掌握了不同类型的题的特点,就可以使问题变的简单明了,本章热点概括为两个概念、一个解法、两个关系、一个应用、三种思想。
一、专题导航
二、考点点拨
考点1 两个概念
概念1一元二次方程的定义
典例剖析1
典例1.若方程是关于x的一元二次方程,则m的值为______________.
答案:
解析:方程是关于x的一元二次方程,
,
解得,
故答案为:.
针对练习1
1.已知是关于x的一元二次方程,则___________.
答案:-1
解析:方程是关于x的一元二次方程,
,,
解得:.
故答案为: 1.
2.若方程是关于x的一元二次方程,则m的值为( )
A.2 B.-2 C.2或-2 D.0
答案:B
解析:由题意得:,解得.
故选:B.
3.如果方程是关于x的一元二次方程,那么m的值为( )
A.±3 B.3 C.-3 D.都不对
答案:C
解析:由题意得:,且,
解得:.
故选:C.
概念2一元二次方程的根
典例剖析2
典例2.若关于x的一元二次方程有一个根是1,则m的值为( )
A.4 B.3 C.2 D.
答案:B
解析:把代入方程得:,解得:.
故选B.
针对练习2
1.已知关于x的一元二次方程.
(1)若.求证:必是该方程的一个根.
(2)当a,b,c之间的关系是_________时,方程必有一根是.
答案:(1)证明见解析
(2)
解析:(1)证明:,,
当时,,
必是该方程的一个根.
(2)当时,,
当时,方程必有一根是.
故答案为.
2.已知实数a是一元二次方程的一个根,求代数式的值.
答案:实数a是一元二次方程的一个根,
,
,
.
3.若是关于x的方程的解,则的值为__________.
答案:2019
解析:把代入方程,得,即,则原式.
考点2 一个解法----一元二次方程的解法
典例剖析3
典例3.用适当的方法解下列方程.
(1);
(2);
(3).
答案:(1),
(2),
(3),
解析:(1)
,
或,
,;
(2)
或,
,;
(3)
或
,.
针对练习3
1.解方程:
(1)(公式法);
(2)(配方法);
(3);
(4).
答案:(1)
(2),
(3),
(4),
解析:(1),
,
解得,,
,;
(2),
,
,
解得,
,;
(3),
,
,
或,
解得,,;
(4),
,
,
,
或,
解得,,.
2.下面是小明解一元二次方程的过程,请认真阅读并完成相应的任务.
二次系数化为1,得………………………………第一步移项,得.……………………………………第二步配方,得,即……………………第三步由此,可得……………………………………第四步所以,,……………………第五步
任务:
(1)上面小明同学的解法中运用“配方法”将该一元二次方程“降次”为两个一元一次方程,体现的数学思想是,其中“配方法”所依据的一个数学公式是;
(2)“第二步”变形的依据是;
(3)上面小明同学解题过程中,从第____步开始出现错误,请直接写出正确的解;
(4)请你根据平时学习经验,就解一元二次方程时还需要注意的事项为其他同学提一条意见.
答案:(1)转化;完全平方公式
(2)等式的基本性质
(3)三;,;
(4)移项要变号
解析:(1)小明同学的解法中运用“配方法”将该一元二次方程“降次”为两个一元一次方程,体现的数学思想是转化思想,其中“配方法”所依据的一个数学公式是完全平方公式;
故答案为:转化;完全平方公式(或填);
(2)“第二步”变形的依据是等式的性质1;
故答案为:等式的性质1;
(3)上面小明同学解题过程中,从第三步开始出现错误;
正确的解是:
配方,得,
即,
,,
故答案为:三;,;
(4)解一元二次方程时需要注意的事项:先把方程化为一般形式、移项要变号、正确运用完全平方公式、解要化为最简(答案不唯一).
3.阅读下面的材料,回答问题:
要解方程,我们发现这是一个一元四次方程,不容易直接求解,如果注意到,根据该方程的特点,我们可以这样做:
解析:设,
那么,
于是原方程可变为,
解得,.
当时,,
;
当时,,
;
原方程有四个根,,,.
我们把以上这种解决问题的方法叫做换元法.
任务:
(1)上述解方程的过程体现的数学思想主要是( )
A.分类讨论思想 B.转化思想 C.数形结合思想 D.公理化思想
(2)仿照上面的方法,解方程;
(3)若实数m、n满足,则的值是__________.
答案:(1)B
(2),,,
(3)4
解析:(1)B.
(2)原方程可以变形为,
设,则原方程可化为,
解得,.
当时,,;
当时,,;
原方程有四个根,,,.
或:设,则原方程可化为,即,
解得,.
当时,,;
当时,,.
原方程有四个根,,,.
(3)4.
考点3 两个关系
关系1一元二次方程的根与判别式的关系
典例剖析4
典例4.若关于x的一元二次方程有两个不相等的实数根,则k的取值范围是( )
A. B.,且 C.,且 D.
答案:B
解析:∵关于x的一元二次方程方程有两个不相等的实数根,
∴,即,
解得:且.
故选:B.
针对练习4
1.已知关于x的一元二次方程,其中m,n在数轴上对应的点如图所示,则这个方程的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
答案:A
解析:由题中数轴得,,,,,
方程有两个不相等的实数根.故选A.
2.已知关于x的一元二次方程有两个相等的实数根,则的值等于( )
A.0 B.1 C.2 D.无法确定
答案:C
解析:关于x的一元二次方程有两个相等的实数根,,,,.故选C.
3.关于x的一元二次方程有实根,则m的最大整数解是( )
A.2 B.3 C.4 D.5
答案:C
解析:关于x的一元二次方程有实根,
且,
解得:且,
m的最大整数解为4,
故选C.
4.已知关于x的一元二次方程,其中a、b、c分别为三边的长.
(1)如果是方程的根,试判断的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断的形状,并说明理由;
(3)如果是等边三角形,试求这个一元二次方程的根.
(1)答案:是等腰三角形,理由见解析
解析:是等腰三角形;
理由:是方程的根,
,
,
,
,
是等腰三角形;
(2)答案:是直角三角形,理由见解析
解析:方程有两个相等的实数根,
,
,
,
是直角三角形;
(3)答案:,
解析:当是等边三角形,
,可整理为:,
,
解得:,.
关系2一元二次方程根与系数的关系
典例剖析5
典例5.如果x、y是两个实数()且,,则的值等于( )
A. B. C. D.2023
答案:C
解析:∵,
∴,
∴,而,,
∴x,是方程的两个根,
∴,,
∴;
故选C.
针对练习5
1.若与是方程的两个实数根,则_________.
答案:4
解析:∵与是方程的两个实数根,
∴,,
∴.
故答案为:4.
2.已知关于x的一元二次方程.
(1)求证:无论m取何值,该方程都有两个不相等的实数根.
(2)设方程的两个根分别为,,且,若,求m的值.
答案:(1)证明见解析
(2)或
解析:(1)证明:由题意得.
无论m取何值,该方程都有两个不相等的实数根.
(2)的两个根分别为,,且,
,,
,,
即,,
解得或.
3.阅读材料:材料1 若一元二次方程的两根为、,则,
材料2:已知实数、满足、,且,求的值.
解:由题知、是方程的两个不相等的实数根,根据材料1得,
根据上述材料解决下面问题:
(1)一元二次方程的两根为、,则=_____,=_____.
(2)已知实数、满足、,且,求的值.
(3)已知实数、满足、,且,求的值.
答案:(1)-2,
(2)-
(3)45
解析:(1)-2,
(2)由题意知:m、n是方程3x2-3x-1=0的两个不相等的实数根,
∴m+n=1,mn=-,
∴m2n+mn2=mn(m+n)=-×1=-.
(3),
,即.
又,即,
∴p、2q是方程的两个不相等的实数根,
,,
.
4.已知,是一元二次方程的两个实数根.
(1)求k的取值范围;
(2)是否存在实数k,使得等式成立?如果存在,请求出k的值,如果不存在,请说明理由.
(1)答案:
解析:一元二次方程有两个实数根,
解得;
(2)答案:
解析:由一元二次方程根与系数关系,,,
,
,
即,解得.
又由(1)知:,
.
考点4 一个应用---一元二次方程的应用
典例剖析6
典例6.如图,老李想用长为的栅栏,再借助房屋的外墙(外墙足够长)围成一个矩形羊圈,并在边上留一个宽的门(建在处,另用其他材料).
(1)当羊圈的长和宽分别为多少米时,能围成一个面积为的羊圈?
(2)羊圈的面积能达到吗?如果能,请你给出设计方案;如果不能,请说明理由.
答案:(1)当羊圈的长为,宽为或长为,宽为时,能围成一个面积为的羊圈
(2)不能,理由见解析
解析:(1)设矩形的边,则边.
根据题意,得.
化简,得.
解得,.
当时,;
当时,.
答:当羊圈的长为,宽为或长为,宽为时,能围成一个面积为的羊圈.
(2)不能,理由如下:
由题意,得.
化简,得.
∵,
∴一元二次方程没有实数根.
∴羊圈的面积不能达到.
针对练习6
1.某商场销售一批衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,商场采取了降价措施.假设在一定范围内,衬衫的单价每降1元,商场平均每天可多售出2件.如果降价后商场销售这批衬衫每天盈利1250元,那么衬衫的单价降了多少元?
答案:衬衫的单价降了15元
解析:设衬衫的单价降了x元.根据题意,得
,
解得:,
答:衬衫的单价降了15元.
2.有一人患了流感,经过两轮传染后共有144人患了流感.
(1)求每轮传染中平均一个人传染了几个人.
(2)如果不及时控制,三轮传染后,患流感的有多少人?
答案:(1)11个人
(2)1728人
解析:(1)设每轮传染中平均一个人传染了x个人,
根据题意,得
解得,(不合题意,舍去).
答:每轮传染中平均一个人传染了11个人.
(2)(人).
答:三轮传染后,患流感的有1728人.
3.某市计划举办青少年足球比赛,赛制采取双循环形式(即每两队之间都要打两场比赛),一共组织30场比赛.计分规则为胜一场得3分,平一场得1分,负一场得0分.
(1)该市举办方应该邀请多少支球队参赛?
(2)此次比赛结束后,如果其中一支参赛球队共平了4场,负了2场,则该球队此次比赛的总积分是多少?
答案:(1)该市举办方应邀请6支球队参赛
(2)该球队此次比赛的总积分是16分
解析:(1)设该市举办方应邀请x支球队参赛.
由题意,得,
解得,(不合题意,舍去).
答:该市举办方应邀请6支球队参赛.
(2)由(1),得30场比赛共6支球队参赛,因此每支球队共比赛10场.
(分).
答:该球队此次比赛的总积分是16分.
4.甲、乙两个机器人分别从相距70米的A,B两个位置同时出发,相向运动.甲第1分钟走了2米,且以后每分钟比前1分钟多走1米,乙每分钟走5米.
(1)甲、乙开始运动多少分钟后第一次相遇?
(2)如果甲、乙到达B或A后立即折返,甲继续每分钟比前1分钟多走1米,乙继续按照每分钟5米的速度行走,那么它们开始运动多少分钟后第二次相遇?
答案:(1)甲、乙开始运动7分钟后第一次相遇
(2)它们开始运动15分钟后第二次相遇
解析:(1)设甲、乙开始运动m分钟后第一次相遇.
依题意,得,
整理,得,
解得,(不合题意,舍去).
答:甲、乙开始运动7分钟后第一次相遇.
(2)设它们开始运动n分钟后第二次相遇.
依题意,得,
整理,得,
解得,(不合题意,舍去).
答:它们开始运动15分钟后第二次相遇.
考点5 三种思想
思想1 整体思想
典例剖析7
典例7.若α,β是方程x2+2x-2005=0的两个实数根,则α2+3α+β的值为( )
A. 2005 B. 2003 C. -2005 D. 4010
【答案】B
【解析】根据一元二次方程根的定义和根与系数的关系求解则可.设x1,x2是关于x的一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的两个实数根,则x1+x2=,x1x2=.而α2+3α+β=α2+2α+(α+β),即可求解.
解:α,β是方程x2+2x-2005=0的两个实数根,则有α+β=-2.
α是方程x2+2x-2005=0的根,得α2+2α-2005=0,即:α2+2α=2005.
所以α2+3α+β=α2+2α+(α+β)=α2+2α-2=2005-2=2003.
故选:B.
针对练习7
1.已知是方程的两个根,则的值为( )
A. 9 B. 10 C. 12 D. 15
【答案】A
【解析】由α、β是方程x2+2017x+1=0的两个根,可得α2+2017α+1=0,β2+2017β+1=0,α+β=-2017,αβ=1,在将(1+2020α+α2)(1+2020β+β2)进行适当的变形,即可求出结果.
∵α,β是方程x2+2017x+1=0的两个根,
∴α2+2017α+1=0,β2+2017β+1=0,α+β=-2017,αβ=1,
∴(1+2020α+α2)(1+2020β+β2)
=(1+2017α+α2+3α)(1+2017β+β2+3β)
=9αβ
=9,
故选:A.
【点睛】考查一元二次方程的根的意义、根与系数的关系,将要求的代数式进行适当的变形,利用整体代入是常用的方法,也是最有效的方法.
2.已知m,n是一元二次方程x2+3x-6=0的两个根,则m2+mn+3m的值为( )
A. 0 B. 3 C. 6 D. 13
【答案】A
【解析】先根据一元二次方程根的定义得到m2+3m=6,根与系数的关系得到mn=-6,然后利用整体代入的方法计算即可.
解:∵m、n是一元二次方程x2+3x-6=0的根,
∴m2+3m-6=0,mn=-6,
即m2+3m=6,
∴m2+mn+3m=m2+3m+mn=6-6=0,
故选:A.
3.阅读材料,解答问题:
已知实数m,n满足m2-m-1=0,n2-n-1=0,且m≠n,则m,n是方程x2-x-1=0的两个不相等的实数根,由韦达定理可知m+n=1,mn=-1.
根据上述材料,解决以下问题:
(1)直接应用:
已知实数a,b满足:a2-7a+1=0,b2-7b+1=0且a≠b,则a+b=_____,ab=_____;
(2)间接应用:
在(1)的条件下,求的值;
(3)拓展应用:
已知实数m,n满足:,n2-n=7且mn≠-1,求的值.
【答案】(1)7;(2)1;
【解析】(1)由韦达定理即可求解;
(2)结合(1)的过程,将平方后变形为+,再代入数据即可得出结论;
(3)令,-n=b,则a2+a-7=0,b2+b-7=0,可得a,b是方程x2+x-7=0的两个不相等的实数根,可得∴,将其代入即可求解.
解:(1)∵实数a,b满足:a2-7a+1=0,b2-7b+1=0且a≠b,
∴a,b是方程x2-7x+1=0的两个不相等的实数根,
∴a+b=7,ab=1.
故答案为:7,1;
(2)由(1)得,()2=++=+=7+2=9,
∴(取正);
(3)令,-n=b,则a2+a-7=0,b2+b-7=0,
∵mn≠-1,
∴,即a≠b,
∴a,b是方程x2+x-7=0的两个不相等的实数根,
∴,
故.
4.阅读材料,解答问题:
材料1
为了解方程(x2)2-13x2+36=0,如果我们把x2看作一个整体,然后设y=x2,则原方程可化为y2-13y+36=0,经过运算,原方程的解为x1,2=±2,x3,4=±3.我们把以上这种解决问题的方法通常叫做换元法.
材料2
已知实数m,n满足m2-m-1=0,n2-n-1=0,且m≠n,显然m,n是方程x2-x-1=0的两个不相等的实数根,由韦达定理可知m+n=1,mn=-1.
根据上述材料,解决以下问题:
(1)直接应用:
方程x4-5x2+6=0的解为 _____;
(2)间接应用:
已知实数a,b满足:2a4-7a2+1=0,2b4-7b2+1=0且a≠b,求a4+b4的值;
(3)拓展应用:
已知实数m,n满足:+=7,n2-n=7且n>0,求+n2的值.
【答案】x1=,x2=-,x3=,x4=-
【解析】(1)利用换元法降次解决问题;
(2)模仿例题解决问题即可;
(3)令=a,-n=b,则a2+a-7=0,b2+b-0,再模仿例题解决问题.
解:(1)令y=x2,则有y2-5y+6=0,
∴(y-2)(y-3)=0,
∴y1=2,y2=3,
∴x2=2或3,
∴x1=,x2=-,x3=,x4=-;
故答案为:x1=,x2=-,x3=,x4=-;
(2)∵a≠b,
∴a2≠b2或a2=b2,
①当a2≠b2时,令a2=m,b2=n.
∴m≠n,则2m2-7m+1=0,2n2-7n+1=0,
∴m,n是方程2x2-7x+1=0的两个不相等的实数根,
∴,
此时a4+b4=m2+n2=(m+n)2-2mn=.
②当a2=b2(a=-b)时,a2=b2=,此时a4+b4=2a4=2(a2)2=,
综上所述,a4+b4=或.
(3)令=a,-n=b,则a2+a-7=0,b2+b-7=0,
∵n>0,
∴≠-n,即a≠b,
∴a,b是方程x2+x-7=0的两个不相等的实数根,
∴,
故+n2=a2+b2=(a+b)2-2ab=15.
思想2 转化思想
典例剖析8
典例8.已知关于y的一元二次方程(m+1)y2-3my-9=0的根都是整数,且m满足等式,则满足条件的所有整数m的和是( )
A. -5 B. -4 C. 0 D. -6
【答案】D
【解析】根据二次根式有意义的条件,根据因式分解法得到方程的解,进一步得到满足条件的所有整数m的和.
解:∵m满足等式,
∴1-m≥0,
解得m≤1,
(m+1)y2-3my-9=0,
(y-3)[(m+1)y+3]=0,
解得y1=3,y2=-,
∵关于y的一元二次方程(m+1)y2-3my-9=0的根都是整数,
∴m=0,-2,-4,
∴满足条件的所有整数m的和是0-2-4=-6.
故选:D.
针对练习8
1.一张桌子的桌面长为6m,宽为4m,台布面积是桌面面积的2倍,如果将台布铺在桌子上,各边垂下的长度相同.求这块台布的长和宽.
【解析】设台布各边垂下的长度是xm,根据“台布面积是桌面面积的2倍”作为相等关系列方程(6+2x)(4+2x)=2×4×6,解方程即可求解.
解:设台布各边垂下的长度是xm,依题意得(6+2x)(4+2x)=2×4×6,
解得x1=-6(不合题意,舍去),x2=1,
所以6+2x=8,
4+2x=6.
答:这块台布的长和宽分别是8m和6m.
2.如图,在宽为20m,长为32m的矩形地上,修筑同样宽的三条道路,把耕地分成大小不等的六块,要使耕地面积为570m2,求道路的宽为多少米?
【解析】把修筑的三条道路分别平移到矩形的最左边和最上边,则剩余的耕地也是一个矩形,设道路的宽为x米,根据矩形面积公式列方程,然后求出解.
解:设道路的宽为x米,
依题意得(32-2x)(20-x)=570,
解得x1=1 x2=35(不符合题意舍去).
答:道路的宽为1米.
3.在北京2008年第29届奥运会前夕,某超市在销售中发现:奥运会吉祥物“福娃”平均每天可售出20套,每件盈利40元.为了迎接奥运会,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存,经市场调查发现:如果每套降价1元,那么平均每天就可多售出2套.要想平均每天在销售吉祥物上盈利1200元,那么每套应降价多少?
【解析】设每套降价x元,那么就多卖出2x套,根据扩大销售量,增加盈利,尽快减少库存,每天在销售吉祥物上盈利1200元,可列方程求解.
解:设每套降价x元,
由题意得:(40-x)(20+2x)=1200
即2x2-60x+400=0,
∴x2-30x+200=0,
∴(x-10)(x-20)=0,
解之得:x=10或x=20
为了减少库存,所以x=20.
每套应降价20元.
思想3 分类讨论思想
典例剖析9
典例9.定义:已知,是关于x的一元二次方程的两个实数根,若,且,则称这个方程为“限根方程”.如:一元二次方程的两根为,,因,,所以一元二次方程为“限根方程”.
请阅读以上材料,回答下列问题:
(1)判断一元二次方程是否为“限根方程”,并说明理由;
(2)若关于x的一元二次方程是“限根方程”,且两根、满足,求k的值;
(3)若关于x的一元二次方程是“限根方程”,求m的取值范围.
答案:(1)此方程为“限根方程”,理由见解析
(2)k的值为2
(3)m的取值范围为或
解析:(1),
,
∴或,
∴,.
∵,,
∴此方程为“限根方程”;
(2)∵方程的两个根分比为、,
∴,.
∵,
∴,
解得:,.
分类讨论:①当时,原方程为,
∴,,
∴,,
∴此时方程是“限根方程”,
∴符合题意;
②当时,原方程为,
∴,,
∴,,
∴此时方程不是“限根方程”,
∴不符合题意.
综上可知k的值为2;
(3),
,
∴或,
∴,或,.
∵此方程为“限根方程”,
∴此方程有两个不相等的实数根,
∴,且,
∴,即,
∴且.
分类讨论:①当时,
∴,,
∵,
∴,
解得:;
②当时,
∴,,
∵,
∴,
解得:.
综上所述,m的取值范围为或.
针对练习9
1.已知关于x的一元二次方程.
(1)求证:不论k取何值,方程总有两个不相等的实数根;
(2)若方程两根的和比两根的积大1,求k的值;
(3)若的两边a,b的长是这个方程的两个实数根,第三边c的长为2,当是等腰三角形时,求k的值.
答案:(1)见解析
(2)k的值为1或2
(3)k的值为2或3
解析:(1)证明:,
,
不论k取何值,方程总有两个不相等的实数根;
(2)设,是关于x的一元二次方程的两个实数根,
,,
方程两根的和比两根的积大1,
,即,
解得或,
故k的值为1或2;
(3)原方程分解因式得:,
,,
的边,,
是等腰三角形,第三边c的长为2,
或,
或3.
,或,,
当,,时,,能构成三角形;
当,,时,,能构成三角形;
故k的值为2或3.
2.已知关于x的方程.
(1)若是方程的一个根,求m的值和方程的另一根;
(2)当m为何实数时,方程有实数根;
(3)若,是方程的两个根,且,试求实数m的值.
答案:(1)另一根为
(2)
(3).
解析:(1)将代入原方程得,
解得:,
设方程的另一根是x,则,
另一根为.
(2)分情况讨论:
当时,方程是一元一次方程,,此时的实数解为;
当m不等于1时,原方程为一元二次方程,要使方程有实数根,
则有,
.
解得:.
即当时,方程有实数根.
(3),.
.
解得:,,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学上点拨与训练
二十一章 一元二次方程
小结与复习
老师告诉你
一元二次方程题型非常广泛,常见有一元二次方程的解,一元二次方程的解法,一元二次方程根的情况,一元二次方程根与系数的关系,一元二次方程的应用等,只要掌握了不同类型的题的特点,就可以使问题变的简单明了,本章热点概括为两个概念、一个解法、两个关系、一个应用、三种思想。
一、专题导航
二、考点点拨
考点1 两个概念
概念1一元二次方程的定义
典例剖析1
典例1.若方程是关于x的一元二次方程,则m的值为______________.
针对练习1
1.已知是关于x的一元二次方程,则___________.
2.若方程是关于x的一元二次方程,则m的值为( )
A.2 B.-2 C.2或-2 D.0
3.如果方程是关于x的一元二次方程,那么m的值为( )
A.±3 B.3 C.-3 D.都不对
概念2一元二次方程的根
典例剖析2
典例2.若关于x的一元二次方程有一个根是1,则m的值为( )
A.4 B.3 C.2 D.
针对练习2
1.已知关于x的一元二次方程.
(1)若.求证:必是该方程的一个根.
(2)当a,b,c之间的关系是_________时,方程必有一根是.
2.已知实数a是一元二次方程的一个根,求代数式的值.
3.若是关于x的方程的解,则的值为__________.
考点2 一个解法----一元二次方程的解法
典例剖析3
典例3.用适当的方法解下列方程.
(1);
(2);
(3).
针对练习3
1.解方程:
(1)(公式法);
(2)(配方法);
(3);
(4).
2.下面是小明解一元二次方程的过程,请认真阅读并完成相应的任务.
二次系数化为1,得………………………………第一步移项,得.……………………………………第二步配方,得,即……………………第三步由此,可得……………………………………第四步所以,,……………………第五步
任务:
(1)上面小明同学的解法中运用“配方法”将该一元二次方程“降次”为两个一元一次方程,体现的数学思想是,其中“配方法”所依据的一个数学公式是;
(2)“第二步”变形的依据是;
(3)上面小明同学解题过程中,从第____步开始出现错误,请直接写出正确的解;
(4)请你根据平时学习经验,就解一元二次方程时还需要注意的事项为其他同学提一条意见.
3.阅读下面的材料,回答问题:
要解方程,我们发现这是一个一元四次方程,不容易直接求解,如果注意到,根据该方程的特点,我们可以这样做:
解析:设,
那么,
于是原方程可变为,
解得,.
当时,,
;
当时,,
;
原方程有四个根,,,.
我们把以上这种解决问题的方法叫做换元法.
任务:
(1)上述解方程的过程体现的数学思想主要是( )
A.分类讨论思想 B.转化思想 C.数形结合思想 D.公理化思想
(2)仿照上面的方法,解方程;
(3)若实数m、n满足,则的值是__________.
考点3 两个关系
关系1一元二次方程的根与判别式的关系
典例剖析4
典例4.若关于x的一元二次方程有两个不相等的实数根,则k的取值范围是( )
A. B.,且 C.,且 D.
针对练习4
1.已知关于x的一元二次方程,其中m,n在数轴上对应的点如图所示,则这个方程的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
2.已知关于x的一元二次方程有两个相等的实数根,则的值等于( )
A.0 B.1 C.2 D.无法确定
3.关于x的一元二次方程有实根,则m的最大整数解是( )
A.2 B.3 C.4 D.5
4.已知关于x的一元二次方程,其中a、b、c分别为三边的长.
(1)如果是方程的根,试判断的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断的形状,并说明理由;
(3)如果是等边三角形,试求这个一元二次方程的根.
关系2一元二次方程根与系数的关系
典例剖析5
典例5.如果x、y是两个实数()且,,则的值等于( )
A. B. C. D.2023
针对练习5
1.若与是方程的两个实数根,则_________.
2.已知关于x的一元二次方程.
(1)求证:无论m取何值,该方程都有两个不相等的实数根.
(2)设方程的两个根分别为,,且,若,求m的值.
3.阅读材料:材料1 若一元二次方程的两根为、,则,
材料2:已知实数、满足、,且,求的值.
解:由题知、是方程的两个不相等的实数根,根据材料1得,
根据上述材料解决下面问题:
(1)一元二次方程的两根为、,则=_____,=_____.
(2)已知实数、满足、,且,求的值.
(3)已知实数、满足、,且,求的值.
4.已知,是一元二次方程的两个实数根.
(1)求k的取值范围;
(2)是否存在实数k,使得等式成立?如果存在,请求出k的值,如果不存在,请说明理由.
考点4 一个应用---一元二次方程的应用
典例剖析6
典例6.如图,老李想用长为的栅栏,再借助房屋的外墙(外墙足够长)围成一个矩形羊圈,并在边上留一个宽的门(建在处,另用其他材料).
(1)当羊圈的长和宽分别为多少米时,能围成一个面积为的羊圈?
(2)羊圈的面积能达到吗?如果能,请你给出设计方案;如果不能,请说明理由.
针对练习6
1.某商场销售一批衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,商场采取了降价措施.假设在一定范围内,衬衫的单价每降1元,商场平均每天可多售出2件.如果降价后商场销售这批衬衫每天盈利1250元,那么衬衫的单价降了多少元?
2.有一人患了流感,经过两轮传染后共有144人患了流感.
(1)求每轮传染中平均一个人传染了几个人.
(2)如果不及时控制,三轮传染后,患流感的有多少人?
.
3.某市计划举办青少年足球比赛,赛制采取双循环形式(即每两队之间都要打两场比赛),一共组织30场比赛.计分规则为胜一场得3分,平一场得1分,负一场得0分.
(1)该市举办方应该邀请多少支球队参赛?
(2)此次比赛结束后,如果其中一支参赛球队共平了4场,负了2场,则该球队此次比赛的总积分是多少?
4.甲、乙两个机器人分别从相距70米的A,B两个位置同时出发,相向运动.甲第1分钟走了2米,且以后每分钟比前1分钟多走1米,乙每分钟走5米.
(1)甲、乙开始运动多少分钟后第一次相遇?
(2)如果甲、乙到达B或A后立即折返,甲继续每分钟比前1分钟多走1米,乙继续按照每分钟5米的速度行走,那么它们开始运动多少分钟后第二次相遇?
考点5 三种思想
思想1 整体思想
典例剖析7
典例7.若α,β是方程x2+2x-2005=0的两个实数根,则α2+3α+β的值为( )
A. 2005 B. 2003 C. -2005 D. 4010
针对练习7
1.已知是方程的两个根,则的值为( )
A. 9 B. 10 C. 12 D. 15
2.已知m,n是一元二次方程x2+3x-6=0的两个根,则m2+mn+3m的值为( )
A. 0 B. 3 C. 6 D. 13
3.阅读材料,解答问题:
已知实数m,n满足m2-m-1=0,n2-n-1=0,且m≠n,则m,n是方程x2-x-1=0的两个不相等的实数根,由韦达定理可知m+n=1,mn=-1.
根据上述材料,解决以下问题:
(1)直接应用:
已知实数a,b满足:a2-7a+1=0,b2-7b+1=0且a≠b,则a+b=_____,ab=_____;
(2)间接应用:
在(1)的条件下,求的值;
(3)拓展应用:
已知实数m,n满足:,n2-n=7且mn≠-1,求的值.
4.阅读材料,解答问题:
材料1
为了解方程(x2)2-13x2+36=0,如果我们把x2看作一个整体,然后设y=x2,则原方程可化为y2-13y+36=0,经过运算,原方程的解为x1,2=±2,x3,4=±3.我们把以上这种解决问题的方法通常叫做换元法.
材料2
已知实数m,n满足m2-m-1=0,n2-n-1=0,且m≠n,显然m,n是方程x2-x-1=0的两个不相等的实数根,由韦达定理可知m+n=1,mn=-1.
根据上述材料,解决以下问题:
(1)直接应用:
方程x4-5x2+6=0的解为 _____;
(2)间接应用:
已知实数a,b满足:2a4-7a2+1=0,2b4-7b2+1=0且a≠b,求a4+b4的值;
(3)拓展应用:
已知实数m,n满足:+=7,n2-n=7且n>0,求+n2的值.
思想2 转化思想
典例剖析8
典例8.已知关于y的一元二次方程(m+1)y2-3my-9=0的根都是整数,且m满足等式,则满足条件的所有整数m的和是( )
A. -5 B. -4 C. 0 D. -6
针对练习8
1.一张桌子的桌面长为6m,宽为4m,台布面积是桌面面积的2倍,如果将台布铺在桌子上,各边垂下的长度相同.求这块台布的长和宽.
2.如图,在宽为20m,长为32m的矩形地上,修筑同样宽的三条道路,把耕地分成大小不等的六块,要使耕地面积为570m2,求道路的宽为多少米?
3.在北京2008年第29届奥运会前夕,某超市在销售中发现:奥运会吉祥物“福娃”平均每天可售出20套,每件盈利40元.为了迎接奥运会,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存,经市场调查发现:如果每套降价1元,那么平均每天就可多售出2套.要想平均每天在销售吉祥物上盈利1200元,那么每套应降价多少?
思想3 分类讨论思想
典例剖析9
典例9.定义:已知,是关于x的一元二次方程的两个实数根,若,且,则称这个方程为“限根方程”.如:一元二次方程的两根为,,因,,所以一元二次方程为“限根方程”.
请阅读以上材料,回答下列问题:
(1)判断一元二次方程是否为“限根方程”,并说明理由;
(2)若关于x的一元二次方程是“限根方程”,且两根、满足,求k的值;
(3)若关于x的一元二次方程是“限根方程”,求m的取值范围.
针对练习9
1.已知关于x的一元二次方程.
(1)求证:不论k取何值,方程总有两个不相等的实数根;
(2)若方程两根的和比两根的积大1,求k的值;
(3)若的两边a,b的长是这个方程的两个实数根,第三边c的长为2,当是等腰三角形时,求k的值.
2.已知关于x的方程.
(1)若是方程的一个根,求m的值和方程的另一根;
(2)当m为何实数时,方程有实数根;
(3)若,是方程的两个根,且,试求实数m的值.
九年级数学上点拨与训练
二十一章 一元二次方程
小结与复习
老师告诉你
一元二次方程题型非常广泛,常见有一元二次方程的解,一元二次方程的解法,一元二次方程根的情况,一元二次方程根与系数的关系,一元二次方程的应用等,只要掌握了不同类型的题的特点,就可以使问题变的简单明了,本章热点概括为两个概念、一个解法、两个关系、一个应用、三种思想。
一、专题导航
二、考点点拨
考点1 两个概念
概念1一元二次方程的定义
典例剖析1
典例1.若方程是关于x的一元二次方程,则m的值为______________.
答案:
解析:方程是关于x的一元二次方程,
,
解得,
故答案为:.
针对练习1
1.已知是关于x的一元二次方程,则___________.
答案:-1
解析:方程是关于x的一元二次方程,
,,
解得:.
故答案为: 1.
2.若方程是关于x的一元二次方程,则m的值为( )
A.2 B.-2 C.2或-2 D.0
答案:B
解析:由题意得:,解得.
故选:B.
3.如果方程是关于x的一元二次方程,那么m的值为( )
A.±3 B.3 C.-3 D.都不对
答案:C
解析:由题意得:,且,
解得:.
故选:C.
概念2一元二次方程的根
典例剖析2
典例2.若关于x的一元二次方程有一个根是1,则m的值为( )
A.4 B.3 C.2 D.
答案:B
解析:把代入方程得:,解得:.
故选B.
针对练习2
1.已知关于x的一元二次方程.
(1)若.求证:必是该方程的一个根.
(2)当a,b,c之间的关系是_________时,方程必有一根是.
答案:(1)证明见解析
(2)
解析:(1)证明:,,
当时,,
必是该方程的一个根.
(2)当时,,
当时,方程必有一根是.
故答案为.
2.已知实数a是一元二次方程的一个根,求代数式的值.
答案:实数a是一元二次方程的一个根,
,
,
.
3.若是关于x的方程的解,则的值为__________.
答案:2019
解析:把代入方程,得,即,则原式.
考点2 一个解法----一元二次方程的解法
典例剖析3
典例3.用适当的方法解下列方程.
(1);
(2);
(3).
答案:(1),
(2),
(3),
解析:(1)
,
或,
,;
(2)
或,
,;
(3)
或
,.
针对练习3
1.解方程:
(1)(公式法);
(2)(配方法);
(3);
(4).
答案:(1)
(2),
(3),
(4),
解析:(1),
,
解得,,
,;
(2),
,
,
解得,
,;
(3),
,
,
或,
解得,,;
(4),
,
,
,
或,
解得,,.
2.下面是小明解一元二次方程的过程,请认真阅读并完成相应的任务.
二次系数化为1,得………………………………第一步移项,得.……………………………………第二步配方,得,即……………………第三步由此,可得……………………………………第四步所以,,……………………第五步
任务:
(1)上面小明同学的解法中运用“配方法”将该一元二次方程“降次”为两个一元一次方程,体现的数学思想是,其中“配方法”所依据的一个数学公式是;
(2)“第二步”变形的依据是;
(3)上面小明同学解题过程中,从第____步开始出现错误,请直接写出正确的解;
(4)请你根据平时学习经验,就解一元二次方程时还需要注意的事项为其他同学提一条意见.
答案:(1)转化;完全平方公式
(2)等式的基本性质
(3)三;,;
(4)移项要变号
解析:(1)小明同学的解法中运用“配方法”将该一元二次方程“降次”为两个一元一次方程,体现的数学思想是转化思想,其中“配方法”所依据的一个数学公式是完全平方公式;
故答案为:转化;完全平方公式(或填);
(2)“第二步”变形的依据是等式的性质1;
故答案为:等式的性质1;
(3)上面小明同学解题过程中,从第三步开始出现错误;
正确的解是:
配方,得,
即,
,,
故答案为:三;,;
(4)解一元二次方程时需要注意的事项:先把方程化为一般形式、移项要变号、正确运用完全平方公式、解要化为最简(答案不唯一).
3.阅读下面的材料,回答问题:
要解方程,我们发现这是一个一元四次方程,不容易直接求解,如果注意到,根据该方程的特点,我们可以这样做:
解析:设,
那么,
于是原方程可变为,
解得,.
当时,,
;
当时,,
;
原方程有四个根,,,.
我们把以上这种解决问题的方法叫做换元法.
任务:
(1)上述解方程的过程体现的数学思想主要是( )
A.分类讨论思想 B.转化思想 C.数形结合思想 D.公理化思想
(2)仿照上面的方法,解方程;
(3)若实数m、n满足,则的值是__________.
答案:(1)B
(2),,,
(3)4
解析:(1)B.
(2)原方程可以变形为,
设,则原方程可化为,
解得,.
当时,,;
当时,,;
原方程有四个根,,,.
或:设,则原方程可化为,即,
解得,.
当时,,;
当时,,.
原方程有四个根,,,.
(3)4.
考点3 两个关系
关系1一元二次方程的根与判别式的关系
典例剖析4
典例4.若关于x的一元二次方程有两个不相等的实数根,则k的取值范围是( )
A. B.,且 C.,且 D.
答案:B
解析:∵关于x的一元二次方程方程有两个不相等的实数根,
∴,即,
解得:且.
故选:B.
针对练习4
1.已知关于x的一元二次方程,其中m,n在数轴上对应的点如图所示,则这个方程的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
答案:A
解析:由题中数轴得,,,,,
方程有两个不相等的实数根.故选A.
2.已知关于x的一元二次方程有两个相等的实数根,则的值等于( )
A.0 B.1 C.2 D.无法确定
答案:C
解析:关于x的一元二次方程有两个相等的实数根,,,,.故选C.
3.关于x的一元二次方程有实根,则m的最大整数解是( )
A.2 B.3 C.4 D.5
答案:C
解析:关于x的一元二次方程有实根,
且,
解得:且,
m的最大整数解为4,
故选C.
4.已知关于x的一元二次方程,其中a、b、c分别为三边的长.
(1)如果是方程的根,试判断的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断的形状,并说明理由;
(3)如果是等边三角形,试求这个一元二次方程的根.
(1)答案:是等腰三角形,理由见解析
解析:是等腰三角形;
理由:是方程的根,
,
,
,
,
是等腰三角形;
(2)答案:是直角三角形,理由见解析
解析:方程有两个相等的实数根,
,
,
,
是直角三角形;
(3)答案:,
解析:当是等边三角形,
,可整理为:,
,
解得:,.
关系2一元二次方程根与系数的关系
典例剖析5
典例5.如果x、y是两个实数()且,,则的值等于( )
A. B. C. D.2023
答案:C
解析:∵,
∴,
∴,而,,
∴x,是方程的两个根,
∴,,
∴;
故选C.
针对练习5
1.若与是方程的两个实数根,则_________.
答案:4
解析:∵与是方程的两个实数根,
∴,,
∴.
故答案为:4.
2.已知关于x的一元二次方程.
(1)求证:无论m取何值,该方程都有两个不相等的实数根.
(2)设方程的两个根分别为,,且,若,求m的值.
答案:(1)证明见解析
(2)或
解析:(1)证明:由题意得.
无论m取何值,该方程都有两个不相等的实数根.
(2)的两个根分别为,,且,
,,
,,
即,,
解得或.
3.阅读材料:材料1 若一元二次方程的两根为、,则,
材料2:已知实数、满足、,且,求的值.
解:由题知、是方程的两个不相等的实数根,根据材料1得,
根据上述材料解决下面问题:
(1)一元二次方程的两根为、,则=_____,=_____.
(2)已知实数、满足、,且,求的值.
(3)已知实数、满足、,且,求的值.
答案:(1)-2,
(2)-
(3)45
解析:(1)-2,
(2)由题意知:m、n是方程3x2-3x-1=0的两个不相等的实数根,
∴m+n=1,mn=-,
∴m2n+mn2=mn(m+n)=-×1=-.
(3),
,即.
又,即,
∴p、2q是方程的两个不相等的实数根,
,,
.
4.已知,是一元二次方程的两个实数根.
(1)求k的取值范围;
(2)是否存在实数k,使得等式成立?如果存在,请求出k的值,如果不存在,请说明理由.
(1)答案:
解析:一元二次方程有两个实数根,
解得;
(2)答案:
解析:由一元二次方程根与系数关系,,,
,
,
即,解得.
又由(1)知:,
.
考点4 一个应用---一元二次方程的应用
典例剖析6
典例6.如图,老李想用长为的栅栏,再借助房屋的外墙(外墙足够长)围成一个矩形羊圈,并在边上留一个宽的门(建在处,另用其他材料).
(1)当羊圈的长和宽分别为多少米时,能围成一个面积为的羊圈?
(2)羊圈的面积能达到吗?如果能,请你给出设计方案;如果不能,请说明理由.
答案:(1)当羊圈的长为,宽为或长为,宽为时,能围成一个面积为的羊圈
(2)不能,理由见解析
解析:(1)设矩形的边,则边.
根据题意,得.
化简,得.
解得,.
当时,;
当时,.
答:当羊圈的长为,宽为或长为,宽为时,能围成一个面积为的羊圈.
(2)不能,理由如下:
由题意,得.
化简,得.
∵,
∴一元二次方程没有实数根.
∴羊圈的面积不能达到.
针对练习6
1.某商场销售一批衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,商场采取了降价措施.假设在一定范围内,衬衫的单价每降1元,商场平均每天可多售出2件.如果降价后商场销售这批衬衫每天盈利1250元,那么衬衫的单价降了多少元?
答案:衬衫的单价降了15元
解析:设衬衫的单价降了x元.根据题意,得
,
解得:,
答:衬衫的单价降了15元.
2.有一人患了流感,经过两轮传染后共有144人患了流感.
(1)求每轮传染中平均一个人传染了几个人.
(2)如果不及时控制,三轮传染后,患流感的有多少人?
答案:(1)11个人
(2)1728人
解析:(1)设每轮传染中平均一个人传染了x个人,
根据题意,得
解得,(不合题意,舍去).
答:每轮传染中平均一个人传染了11个人.
(2)(人).
答:三轮传染后,患流感的有1728人.
3.某市计划举办青少年足球比赛,赛制采取双循环形式(即每两队之间都要打两场比赛),一共组织30场比赛.计分规则为胜一场得3分,平一场得1分,负一场得0分.
(1)该市举办方应该邀请多少支球队参赛?
(2)此次比赛结束后,如果其中一支参赛球队共平了4场,负了2场,则该球队此次比赛的总积分是多少?
答案:(1)该市举办方应邀请6支球队参赛
(2)该球队此次比赛的总积分是16分
解析:(1)设该市举办方应邀请x支球队参赛.
由题意,得,
解得,(不合题意,舍去).
答:该市举办方应邀请6支球队参赛.
(2)由(1),得30场比赛共6支球队参赛,因此每支球队共比赛10场.
(分).
答:该球队此次比赛的总积分是16分.
4.甲、乙两个机器人分别从相距70米的A,B两个位置同时出发,相向运动.甲第1分钟走了2米,且以后每分钟比前1分钟多走1米,乙每分钟走5米.
(1)甲、乙开始运动多少分钟后第一次相遇?
(2)如果甲、乙到达B或A后立即折返,甲继续每分钟比前1分钟多走1米,乙继续按照每分钟5米的速度行走,那么它们开始运动多少分钟后第二次相遇?
答案:(1)甲、乙开始运动7分钟后第一次相遇
(2)它们开始运动15分钟后第二次相遇
解析:(1)设甲、乙开始运动m分钟后第一次相遇.
依题意,得,
整理,得,
解得,(不合题意,舍去).
答:甲、乙开始运动7分钟后第一次相遇.
(2)设它们开始运动n分钟后第二次相遇.
依题意,得,
整理,得,
解得,(不合题意,舍去).
答:它们开始运动15分钟后第二次相遇.
考点5 三种思想
思想1 整体思想
典例剖析7
典例7.若α,β是方程x2+2x-2005=0的两个实数根,则α2+3α+β的值为( )
A. 2005 B. 2003 C. -2005 D. 4010
【答案】B
【解析】根据一元二次方程根的定义和根与系数的关系求解则可.设x1,x2是关于x的一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的两个实数根,则x1+x2=,x1x2=.而α2+3α+β=α2+2α+(α+β),即可求解.
解:α,β是方程x2+2x-2005=0的两个实数根,则有α+β=-2.
α是方程x2+2x-2005=0的根,得α2+2α-2005=0,即:α2+2α=2005.
所以α2+3α+β=α2+2α+(α+β)=α2+2α-2=2005-2=2003.
故选:B.
针对练习7
1.已知是方程的两个根,则的值为( )
A. 9 B. 10 C. 12 D. 15
【答案】A
【解析】由α、β是方程x2+2017x+1=0的两个根,可得α2+2017α+1=0,β2+2017β+1=0,α+β=-2017,αβ=1,在将(1+2020α+α2)(1+2020β+β2)进行适当的变形,即可求出结果.
∵α,β是方程x2+2017x+1=0的两个根,
∴α2+2017α+1=0,β2+2017β+1=0,α+β=-2017,αβ=1,
∴(1+2020α+α2)(1+2020β+β2)
=(1+2017α+α2+3α)(1+2017β+β2+3β)
=9αβ
=9,
故选:A.
【点睛】考查一元二次方程的根的意义、根与系数的关系,将要求的代数式进行适当的变形,利用整体代入是常用的方法,也是最有效的方法.
2.已知m,n是一元二次方程x2+3x-6=0的两个根,则m2+mn+3m的值为( )
A. 0 B. 3 C. 6 D. 13
【答案】A
【解析】先根据一元二次方程根的定义得到m2+3m=6,根与系数的关系得到mn=-6,然后利用整体代入的方法计算即可.
解:∵m、n是一元二次方程x2+3x-6=0的根,
∴m2+3m-6=0,mn=-6,
即m2+3m=6,
∴m2+mn+3m=m2+3m+mn=6-6=0,
故选:A.
3.阅读材料,解答问题:
已知实数m,n满足m2-m-1=0,n2-n-1=0,且m≠n,则m,n是方程x2-x-1=0的两个不相等的实数根,由韦达定理可知m+n=1,mn=-1.
根据上述材料,解决以下问题:
(1)直接应用:
已知实数a,b满足:a2-7a+1=0,b2-7b+1=0且a≠b,则a+b=_____,ab=_____;
(2)间接应用:
在(1)的条件下,求的值;
(3)拓展应用:
已知实数m,n满足:,n2-n=7且mn≠-1,求的值.
【答案】(1)7;(2)1;
【解析】(1)由韦达定理即可求解;
(2)结合(1)的过程,将平方后变形为+,再代入数据即可得出结论;
(3)令,-n=b,则a2+a-7=0,b2+b-7=0,可得a,b是方程x2+x-7=0的两个不相等的实数根,可得∴,将其代入即可求解.
解:(1)∵实数a,b满足:a2-7a+1=0,b2-7b+1=0且a≠b,
∴a,b是方程x2-7x+1=0的两个不相等的实数根,
∴a+b=7,ab=1.
故答案为:7,1;
(2)由(1)得,()2=++=+=7+2=9,
∴(取正);
(3)令,-n=b,则a2+a-7=0,b2+b-7=0,
∵mn≠-1,
∴,即a≠b,
∴a,b是方程x2+x-7=0的两个不相等的实数根,
∴,
故.
4.阅读材料,解答问题:
材料1
为了解方程(x2)2-13x2+36=0,如果我们把x2看作一个整体,然后设y=x2,则原方程可化为y2-13y+36=0,经过运算,原方程的解为x1,2=±2,x3,4=±3.我们把以上这种解决问题的方法通常叫做换元法.
材料2
已知实数m,n满足m2-m-1=0,n2-n-1=0,且m≠n,显然m,n是方程x2-x-1=0的两个不相等的实数根,由韦达定理可知m+n=1,mn=-1.
根据上述材料,解决以下问题:
(1)直接应用:
方程x4-5x2+6=0的解为 _____;
(2)间接应用:
已知实数a,b满足:2a4-7a2+1=0,2b4-7b2+1=0且a≠b,求a4+b4的值;
(3)拓展应用:
已知实数m,n满足:+=7,n2-n=7且n>0,求+n2的值.
【答案】x1=,x2=-,x3=,x4=-
【解析】(1)利用换元法降次解决问题;
(2)模仿例题解决问题即可;
(3)令=a,-n=b,则a2+a-7=0,b2+b-0,再模仿例题解决问题.
解:(1)令y=x2,则有y2-5y+6=0,
∴(y-2)(y-3)=0,
∴y1=2,y2=3,
∴x2=2或3,
∴x1=,x2=-,x3=,x4=-;
故答案为:x1=,x2=-,x3=,x4=-;
(2)∵a≠b,
∴a2≠b2或a2=b2,
①当a2≠b2时,令a2=m,b2=n.
∴m≠n,则2m2-7m+1=0,2n2-7n+1=0,
∴m,n是方程2x2-7x+1=0的两个不相等的实数根,
∴,
此时a4+b4=m2+n2=(m+n)2-2mn=.
②当a2=b2(a=-b)时,a2=b2=,此时a4+b4=2a4=2(a2)2=,
综上所述,a4+b4=或.
(3)令=a,-n=b,则a2+a-7=0,b2+b-7=0,
∵n>0,
∴≠-n,即a≠b,
∴a,b是方程x2+x-7=0的两个不相等的实数根,
∴,
故+n2=a2+b2=(a+b)2-2ab=15.
思想2 转化思想
典例剖析8
典例8.已知关于y的一元二次方程(m+1)y2-3my-9=0的根都是整数,且m满足等式,则满足条件的所有整数m的和是( )
A. -5 B. -4 C. 0 D. -6
【答案】D
【解析】根据二次根式有意义的条件,根据因式分解法得到方程的解,进一步得到满足条件的所有整数m的和.
解:∵m满足等式,
∴1-m≥0,
解得m≤1,
(m+1)y2-3my-9=0,
(y-3)[(m+1)y+3]=0,
解得y1=3,y2=-,
∵关于y的一元二次方程(m+1)y2-3my-9=0的根都是整数,
∴m=0,-2,-4,
∴满足条件的所有整数m的和是0-2-4=-6.
故选:D.
针对练习8
1.一张桌子的桌面长为6m,宽为4m,台布面积是桌面面积的2倍,如果将台布铺在桌子上,各边垂下的长度相同.求这块台布的长和宽.
【解析】设台布各边垂下的长度是xm,根据“台布面积是桌面面积的2倍”作为相等关系列方程(6+2x)(4+2x)=2×4×6,解方程即可求解.
解:设台布各边垂下的长度是xm,依题意得(6+2x)(4+2x)=2×4×6,
解得x1=-6(不合题意,舍去),x2=1,
所以6+2x=8,
4+2x=6.
答:这块台布的长和宽分别是8m和6m.
2.如图,在宽为20m,长为32m的矩形地上,修筑同样宽的三条道路,把耕地分成大小不等的六块,要使耕地面积为570m2,求道路的宽为多少米?
【解析】把修筑的三条道路分别平移到矩形的最左边和最上边,则剩余的耕地也是一个矩形,设道路的宽为x米,根据矩形面积公式列方程,然后求出解.
解:设道路的宽为x米,
依题意得(32-2x)(20-x)=570,
解得x1=1 x2=35(不符合题意舍去).
答:道路的宽为1米.
3.在北京2008年第29届奥运会前夕,某超市在销售中发现:奥运会吉祥物“福娃”平均每天可售出20套,每件盈利40元.为了迎接奥运会,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存,经市场调查发现:如果每套降价1元,那么平均每天就可多售出2套.要想平均每天在销售吉祥物上盈利1200元,那么每套应降价多少?
【解析】设每套降价x元,那么就多卖出2x套,根据扩大销售量,增加盈利,尽快减少库存,每天在销售吉祥物上盈利1200元,可列方程求解.
解:设每套降价x元,
由题意得:(40-x)(20+2x)=1200
即2x2-60x+400=0,
∴x2-30x+200=0,
∴(x-10)(x-20)=0,
解之得:x=10或x=20
为了减少库存,所以x=20.
每套应降价20元.
思想3 分类讨论思想
典例剖析9
典例9.定义:已知,是关于x的一元二次方程的两个实数根,若,且,则称这个方程为“限根方程”.如:一元二次方程的两根为,,因,,所以一元二次方程为“限根方程”.
请阅读以上材料,回答下列问题:
(1)判断一元二次方程是否为“限根方程”,并说明理由;
(2)若关于x的一元二次方程是“限根方程”,且两根、满足,求k的值;
(3)若关于x的一元二次方程是“限根方程”,求m的取值范围.
答案:(1)此方程为“限根方程”,理由见解析
(2)k的值为2
(3)m的取值范围为或
解析:(1),
,
∴或,
∴,.
∵,,
∴此方程为“限根方程”;
(2)∵方程的两个根分比为、,
∴,.
∵,
∴,
解得:,.
分类讨论:①当时,原方程为,
∴,,
∴,,
∴此时方程是“限根方程”,
∴符合题意;
②当时,原方程为,
∴,,
∴,,
∴此时方程不是“限根方程”,
∴不符合题意.
综上可知k的值为2;
(3),
,
∴或,
∴,或,.
∵此方程为“限根方程”,
∴此方程有两个不相等的实数根,
∴,且,
∴,即,
∴且.
分类讨论:①当时,
∴,,
∵,
∴,
解得:;
②当时,
∴,,
∵,
∴,
解得:.
综上所述,m的取值范围为或.
针对练习9
1.已知关于x的一元二次方程.
(1)求证:不论k取何值,方程总有两个不相等的实数根;
(2)若方程两根的和比两根的积大1,求k的值;
(3)若的两边a,b的长是这个方程的两个实数根,第三边c的长为2,当是等腰三角形时,求k的值.
答案:(1)见解析
(2)k的值为1或2
(3)k的值为2或3
解析:(1)证明:,
,
不论k取何值,方程总有两个不相等的实数根;
(2)设,是关于x的一元二次方程的两个实数根,
,,
方程两根的和比两根的积大1,
,即,
解得或,
故k的值为1或2;
(3)原方程分解因式得:,
,,
的边,,
是等腰三角形,第三边c的长为2,
或,
或3.
,或,,
当,,时,,能构成三角形;
当,,时,,能构成三角形;
故k的值为2或3.
2.已知关于x的方程.
(1)若是方程的一个根,求m的值和方程的另一根;
(2)当m为何实数时,方程有实数根;
(3)若,是方程的两个根,且,试求实数m的值.
答案:(1)另一根为
(2)
(3).
解析:(1)将代入原方程得,
解得:,
设方程的另一根是x,则,
另一根为.
(2)分情况讨论:
当时,方程是一元一次方程,,此时的实数解为;
当m不等于1时,原方程为一元二次方程,要使方程有实数根,
则有,
.
解得:.
即当时,方程有实数根.
(3),.
.
解得:,,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
