七年级数学上册3.5 二元一次方程组的应用 导学案(知识清单 典型例题 巩固提升)
文档属性
| 名称 | 七年级数学上册3.5 二元一次方程组的应用 导学案(知识清单 典型例题 巩固提升) |

|
|
| 格式 | docx | ||
| 文件大小 | 529.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-11 12:28:07 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
3.5 二元一次方程组的应用 导学案
(一)学习目标:
1使学生会借助二元一次方程组解决简单的实际问题,再次体会二元一次方程组与现实生活的联系和作用
2通过应用题教学使学生进一步使用代数中的方程去反映现实世界中等量关系,体会代数方法的优越性
3体会列方程组比列一元一次方程容易
4进一步培养化实际问题为数学问题的能力和分析问题,解决问题的能力
(二)学习重难点:
1.以方程组为工具分析、解决含有多个未知数的实际问题
2.正确找出问题中的两个等量关系,并根据题意列二元一次方程组
阅读课本,识记知识:
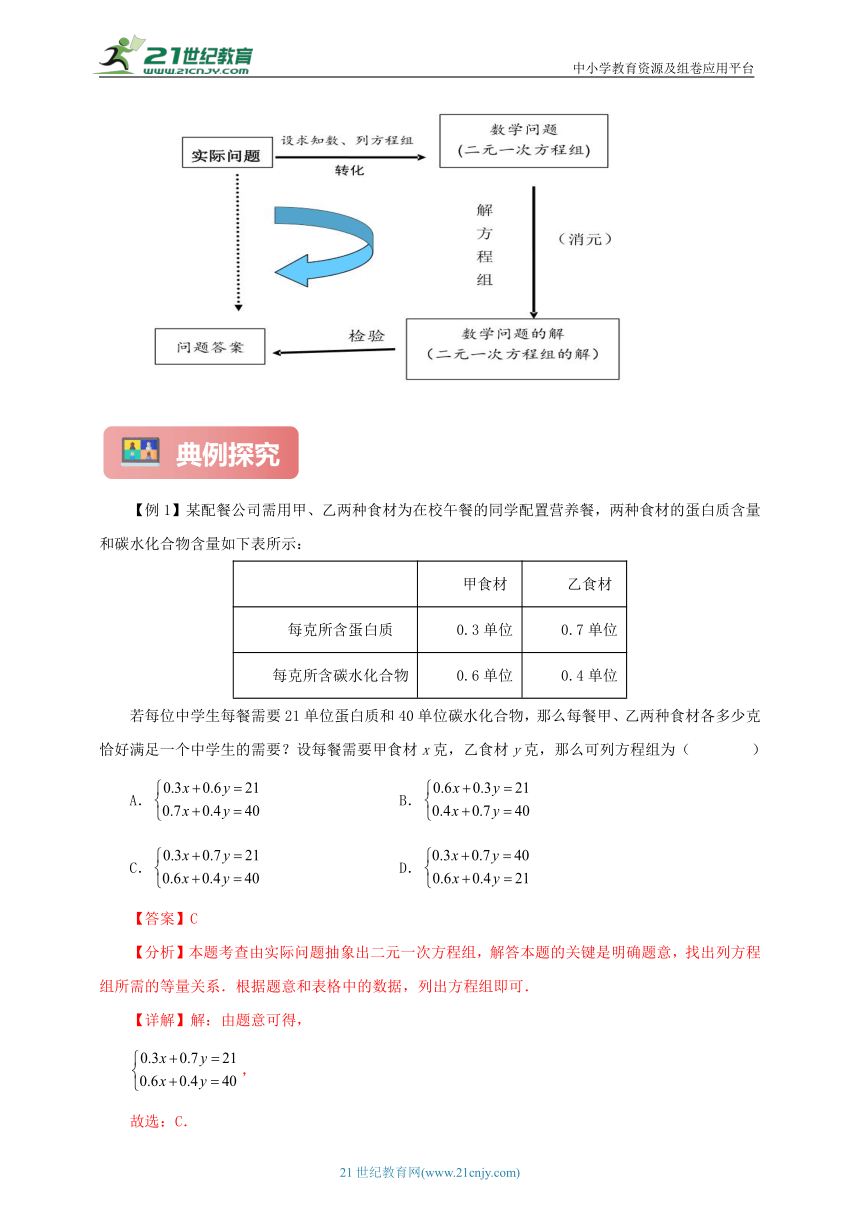
列二元一次方程解决实际问题的一般步骤:
1.审:确定已知量和未知量
2.设:用字母表示题目中的两个未知数。
3.列:根据题意找到两等量关系并列出方程组。
4.解:解方程组,求出未知数的值。
5.答:检验所求的解,写出答案。
注意:应用题审题是前提,找等量关系是关键;单位一定要统一;“设”、“答”两步,都要写清单位名称。
【例1】某配餐公司需用甲、乙两种食材为在校午餐的同学配置营养餐,两种食材的蛋白质含量和碳水化合物含量如下表所示:
甲食材 乙食材
每克所含蛋白质 0.3单位 0.7单位
每克所含碳水化合物 0.6单位 0.4单位
若每位中学生每餐需要21单位蛋白质和40单位碳水化合物,那么每餐甲、乙两种食材各多少克恰好满足一个中学生的需要?设每餐需要甲食材x克,乙食材y克,那么可列方程组为( )
A. B.
C. D.
【答案】C
【分析】本题考查由实际问题抽象出二元一次方程组,解答本题的关键是明确题意,找出列方程组所需的等量关系.根据题意和表格中的数据,列出方程组即可.
【详解】解:由题意可得,
,
故选:C.
【例2】 一停车场上有辆车,其中一辆汽车有个轮子,一辆摩托车有个轮子,且停车场只有汽车和摩托车,这些车共有个轮子,那么摩托车应为( )
A.辆 B.辆 C.辆 D.辆
【答案】D
【分析】本题考查了二元一次方程组的实际应用,读懂题意,根据题目给出的条件,找到合适的等量关系,列出方程组,求解方程组,是解答本题的关键.
根据题意,设摩托车应为辆,汽车辆,由此列出二元一次方程组,解出方程组,得到答案.
【详解】解:根据题意设:
摩托车应为辆,汽车辆,
则,
解得,
摩托车应为辆,
故答案为:.
选择题
1.《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木头的长、绳子还剩余尺;将绳子对折再量木头,则木头还剩余1尺,问木头长多少尺?可设木头长为x尺,绳子长为y尺,则所列方程组正确的是( )
A. B.
C. D.
2.甲、乙两地相距100千米,一艘轮船往返两地,顺流用4小时,逆流用5小时,那么这艘轮船在静水中的航速与水速分别是( )
A.24千米/时,8千米/时 B.22.5千米/时,2.5千米/时
C.18千米/时,24千米/时 D.12.5千米/时,1.5千米/时
3.两位同学在解方程组时,甲同学正确地解出,乙同学因把c抄错了解得,则a、b、c正确的值应为( )
A. B.
C. D.
4.某班为了奖励取得较大进步的同学,花了 元购买了甲、乙两种奖品共30件,其中甲种奖品每件16元,乙种奖品每件12元. 求甲、乙两种奖品各买了多少件?若设买了甲种奖品件,乙种奖品件,则下列所列方程组中正确的是( )
A. B.
C. D.
5.某个体商店在一次买卖中同时卖出两件上衣,每件都是以135元卖出,若按成本计算,其中一件赢利25%,另一件亏损25%,则这家商店在这次买卖中( )
A.不赔不赚 B.赚9元 C.赔8元 D.赔18元
6.作业本中有这样一道题:“小明去郊游,上午8时30分从家中出发,先走平路,然后登山,中午12时到达山顶,原地休息后沿原路返回,正好下午3时到家.若他平路每小时走,登山每小时走,下山每小时走,求小明家到山顶的路程.”小李查看解答时发现答案中的方程组中有污损:则答案中另一个方程应为( )
A. B.
C. D.
7.已知甲、乙两数之和是42,甲数的3倍等于乙数的4倍,求甲、乙两数.若设甲数为x,乙数为y,由题意得方程组( )
A. B.
C. D.
8.现有一段长为5000米的马路需要整修,由甲、乙两个工程小组先后接力完成,甲工程小组每天整修200米,乙工程小组每天整修250米,共用时22天.设甲工程小组整修马路米,乙工程小组整修马路米,依题意可列方程组( )
A. B.
C. D.
9.2023年杭州亚运会期间,吉祥物琼琼、宸宸、莲莲因其灵动可爱的形象受到了大家的喜爱.为了提高销量,某店家推出了吉祥物套装礼盒,一个套装礼盒里包含1个吉祥物宸宸玩偶和2个其他吉祥物的钥匙扣.已知一个玩偶的进价为60元,一个钥匙扣的进价为20元,该店家计划用5000元购进一批玩偶和钥匙扣,使得刚好配套,设购进x个玩偶,y个钥匙扣,则下列方程组正确的是( )
A. B.
C. D.
10.将浓度为的酒精与浓度为的酒精混合,制成了浓度为的酒精,设浓度为的酒精需要,浓度为的酒精需要,则列出的方程组为( )
A. B.
C. D.
填空题
11. 如图是由7个形状、大小都相同的小长方形和阴影部分无缝隙拼合而成的一个大长方形,则图中阴影部分的面积为 .
12.一个两位数,个位上的数比十位上的数的2倍多1,若将十位数字与个位数字调换位置,则比原两位数的2倍还多2,则原两位数是。
13.上学年初一某班的学生都是两人一桌,其中男生与女生同桌,这些女生占全班女生的.本学年该班新转入4个男生后,男女生刚好一样多.设上学年该班有男生x人,女生y人,则列方程组为 .
14.端午节时,王老师用72元钱买了荷包和五彩绳共20个(条),其中荷包每个4元,五彩绳每条3元,设王老师购买荷包x个,五彩绳y条,根据题意,列出的方程组是________.
15.已知点沿x轴正方向向右上方做跳马运动(即中国象棋“日”字型跳跃).若跳到位置,称为做一次“正横跳马”;若跳到位置,称为做一次“正竖跳马”,当点P连续做了a次“正横跳马”和b次“正竖跳马”后,到达点,则的值是 .
三、解答题
16.某长甲车间人数比乙车间人数的还少30人,如果从乙车间调10人到甲车间,那么甲车间的人数是乙车间的,求两个车间原来各有多少人?
17.一批货物要运往某地,货主准备租用汽运公司的甲、乙两种货车.已知最近两次租用这两种货车运货的情况如下表:
甲货车辆数 乙货车辆数 累计运货吨数
第一次 3 4 54
第二次 2 3 39
(1)1辆甲货车和1辆乙货车一次分别运货多少吨?
(2)若货主现有45t货物,计划同时租用甲货车a辆,乙货车b辆(a,b均为正整数),一次运完,且恰好每辆车都装满货物.请你帮助货主设计租车方案.
18.2023上海国际车展于2023年4月18日正式开幕,新能源汽车成为本次车展的亮点.某汽车销售公司计划购进一批新能源汽车尝试进行销售,据了解1辆A型新能源汽车、3辆B型新能源汽车的进价共计55万元;4辆A型新能源汽车、2辆B型新能源汽车的进价共计120万元.
(1)求A、B两种型号的新能源汽车每辆的进价分别为多少万元;
(2)若该公司计划正好用200万元购进以上两种型号的新能源汽车(两种型号的新能源汽车均购买),请你通过计算帮该公司求出全部的购买方案.
(一)课后反思:
本节课我学会了:
本节课存在的问题:
把本节课所学知识画出思维导图
参考答案
1.【答案】A
【分析】本题主要考查了从实际问题中抽象出二元一次方程组,设木头长为x尺,绳子长为y尺,根据用一根绳子去量一根木头的长、绳子还剩余尺,可得,根据将绳子对折再量木头,则木头还剩余1尺可得,据此列出方程组即可.
【详解】解;设木头长为x尺,绳子长为y尺,
由题意得,,
故选A.
【答案】B
【解析】略
3.【答案】C
【分析】本题主要考查了二元一次方程组的错解问题,解题的关键是理解题意得出正确的方程组.把甲的结果代入方程组两方程中,乙的结果代入第一个方程中,分别求出a,b,c的值,即可求出所求.
【详解】解:解:把代入方程组得: ,
把代入得:,
联立得:,解得:,
由,得到,
故选:C.
4.【答案】D
【分析】此题主要考查了由实际问题抽象出二元一次方程组,解题的关键是正确理解题意,抓住关键语句,找出等量关系.
根据题意可得等量关系:①甲商品数量+乙商品数量=30件;②甲商品的总价+乙商品的总价=400,然后列出方程组即可.
【详解】解:设买了甲种奖品件,乙种奖品件,依题意得:
,
故选:D
【答案】D
【解析】略
6.【答案】D
【解析】略
7.【答案】B
【解析】略
8.【答案】C
【分析】本题考查了二元一次方程组的实际应用,找准等量关系,正确列出二元一次方程组是解答本题的关键.
根据题意,找到两个等量关系:甲工程小组整修马路的长度乙工程小组整修马路的长度米,甲工程小组整修马路的天数乙工程小组整修马路的天数天,由此列出方程组,得到答案.
【详解】解:根据题意,
设甲工程小组整修马路米,乙工程小组整修马路米,
依题意可列方程组:
,
故选:.
9.【答案】C
【分析】本题考查了由实际问题抽象出二元一次方程组,利用总价单价数量,结合购进玩偶和钥匙扣数量间的关系,即可列出关于x,y的二元一次方程组,此题得解.找准等量关系,正确列出二元一次方程组是解题的关键.
【详解】解:∵一个套装礼盒里包含1个吉祥物宸宸玩偶和2个其他吉祥物的钥匙扣,
∴购进钥匙扣的数量是购进宸宸玩偶数量的2倍,
∴;
∵一个玩偶的进价为60元,一个钥匙扣的进价为20元,且店家共花费5000元,
∴.
根据题意可列出方程组.
故选:C.
10.【答案】C
【分析】本题考查列二元一次方程组解决实际问题,能够根据题意找出等量关系,并根据等量关系列出方程组是解决本题的关键.
【详解】解:的酒精质量加上浓度为的酒精质量等于,
的酒精中酒精质量加上浓度为的酒精中酒精质量等于混合后的液体中所含的酒精质量,
由此可知方程组为,
故选:C.
11.【答案】36
【分析】本题考查了二元一次方程组的应用,设小长方形的长为x,宽为y,则小正方形的边长为,根据图中各边之间的关系列出关于x,y的二元一次方程组,解之即可得出x,y的值,再利用正方形的面积公式计算即可.找准等量关系,正确列出二元一次方程组是解题的关键.
【详解】解:设小长方形的长为x,宽为y,则小正方形的边长为,
依题意得:,解得:,
∴图中阴影部分的面积为.
故答案为36.
【答案】25
【解析】略
13.【答案】
【分析】本题考查由实际问题抽象出二元一次方程组.根据本学年该班新转入4个男生后,男女生刚好一样多,其中男生与女生同桌,这些女生占全班女生的,可以列出相应的方程组.
【详解】解:由题意可得,
,
故答案为:.
14.【答案】14,6
【解析】略
15.【答案】
【分析】此题考查了点的坐标以及二元一次方程组的应用,读懂题意,正确列出方程组是解题的关键.由题意可得:做一次“正横跳马”横坐标增加2,纵坐标增加1,做一次“正竖跳马”横坐标增加1,纵坐标增加2,据此列方程组进行求解即可.
【详解】解:由题意,当点先连续做了a次“正横跳马”,再连续做b次“正竖跳马”后,到达点,则:
,
,得:,
∴;
故答案为:.
16.设甲车间有人,乙车间有人,根据题意,得
解得
答:甲车间有170人,乙车间有250人。
17.【答案】(1)1辆甲货车一次运货6t,1辆乙货车一次运货9t
(2)有2种租车方案.方案1:租用3辆甲货车,3辆乙货车;方案2:租用6辆甲货车,1辆乙货车
【详解】解:(1)设1辆甲货车一次运货xt,1辆乙货车一次运货yt.
根据题意,得解得
故1辆甲货车一次运货6t,1辆乙货车一次运货9t.
(2)根据题意,得,.
又a,b均为正整数,或
有2种租车方案.方案1:租用3辆甲货车,3辆乙货车;方案2:租用6辆甲货车,1辆乙货车.
18.【答案】(1)A、B两种型号的汽车每辆进价分别为25万元和10万元
(2)购买A型号汽车2辆,B型号汽车15辆;购买A型号汽车4辆,B型号汽车10辆;购买A型号汽车6辆,B型号汽车5辆.
【分析】本题主要考查了二元一次方程组的应用,解题的关键是根据等量关系列出方程,准确解方程.
(1)设A、B两种型号的汽车每辆进价分别为x万元,y万元,根据1辆A型新能源汽车、3辆B型新能源汽车的进价共计55万元;4辆A型新能源汽车、2辆B型新能源汽车的进价共计120万元列出方程组,解方程组即可;
(2)设购进A型号汽车m辆,B型号汽车n辆,根据该公司计划正好用200万元购进以上两种型号的新能源汽车,列出二元一次方程,根据、n为正整数,求出方程的解,得出结果即可.
【详解】(1)解:设A、B两种型号的汽车每辆进价分别为x万元,y万元,根据题意得:
,
解得:,
答:A、B两种型号的汽车每辆进价分别为25万元和10万元;
(2)解:设购进A型号汽车m辆,B型号汽车n辆,根据题意得:
,
∴,
∵、n为正整数,
∴,,,
∴购买A型号汽车2辆,B型号汽车15辆;
购买A型号汽车4辆,B型号汽车10辆;
购买A型号汽车6辆,B型号汽车5辆.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.5 二元一次方程组的应用 导学案
(一)学习目标:
1使学生会借助二元一次方程组解决简单的实际问题,再次体会二元一次方程组与现实生活的联系和作用
2通过应用题教学使学生进一步使用代数中的方程去反映现实世界中等量关系,体会代数方法的优越性
3体会列方程组比列一元一次方程容易
4进一步培养化实际问题为数学问题的能力和分析问题,解决问题的能力
(二)学习重难点:
1.以方程组为工具分析、解决含有多个未知数的实际问题
2.正确找出问题中的两个等量关系,并根据题意列二元一次方程组
阅读课本,识记知识:
列二元一次方程解决实际问题的一般步骤:
1.审:确定已知量和未知量
2.设:用字母表示题目中的两个未知数。
3.列:根据题意找到两等量关系并列出方程组。
4.解:解方程组,求出未知数的值。
5.答:检验所求的解,写出答案。
注意:应用题审题是前提,找等量关系是关键;单位一定要统一;“设”、“答”两步,都要写清单位名称。
【例1】某配餐公司需用甲、乙两种食材为在校午餐的同学配置营养餐,两种食材的蛋白质含量和碳水化合物含量如下表所示:
甲食材 乙食材
每克所含蛋白质 0.3单位 0.7单位
每克所含碳水化合物 0.6单位 0.4单位
若每位中学生每餐需要21单位蛋白质和40单位碳水化合物,那么每餐甲、乙两种食材各多少克恰好满足一个中学生的需要?设每餐需要甲食材x克,乙食材y克,那么可列方程组为( )
A. B.
C. D.
【答案】C
【分析】本题考查由实际问题抽象出二元一次方程组,解答本题的关键是明确题意,找出列方程组所需的等量关系.根据题意和表格中的数据,列出方程组即可.
【详解】解:由题意可得,
,
故选:C.
【例2】 一停车场上有辆车,其中一辆汽车有个轮子,一辆摩托车有个轮子,且停车场只有汽车和摩托车,这些车共有个轮子,那么摩托车应为( )
A.辆 B.辆 C.辆 D.辆
【答案】D
【分析】本题考查了二元一次方程组的实际应用,读懂题意,根据题目给出的条件,找到合适的等量关系,列出方程组,求解方程组,是解答本题的关键.
根据题意,设摩托车应为辆,汽车辆,由此列出二元一次方程组,解出方程组,得到答案.
【详解】解:根据题意设:
摩托车应为辆,汽车辆,
则,
解得,
摩托车应为辆,
故答案为:.
选择题
1.《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木头的长、绳子还剩余尺;将绳子对折再量木头,则木头还剩余1尺,问木头长多少尺?可设木头长为x尺,绳子长为y尺,则所列方程组正确的是( )
A. B.
C. D.
2.甲、乙两地相距100千米,一艘轮船往返两地,顺流用4小时,逆流用5小时,那么这艘轮船在静水中的航速与水速分别是( )
A.24千米/时,8千米/时 B.22.5千米/时,2.5千米/时
C.18千米/时,24千米/时 D.12.5千米/时,1.5千米/时
3.两位同学在解方程组时,甲同学正确地解出,乙同学因把c抄错了解得,则a、b、c正确的值应为( )
A. B.
C. D.
4.某班为了奖励取得较大进步的同学,花了 元购买了甲、乙两种奖品共30件,其中甲种奖品每件16元,乙种奖品每件12元. 求甲、乙两种奖品各买了多少件?若设买了甲种奖品件,乙种奖品件,则下列所列方程组中正确的是( )
A. B.
C. D.
5.某个体商店在一次买卖中同时卖出两件上衣,每件都是以135元卖出,若按成本计算,其中一件赢利25%,另一件亏损25%,则这家商店在这次买卖中( )
A.不赔不赚 B.赚9元 C.赔8元 D.赔18元
6.作业本中有这样一道题:“小明去郊游,上午8时30分从家中出发,先走平路,然后登山,中午12时到达山顶,原地休息后沿原路返回,正好下午3时到家.若他平路每小时走,登山每小时走,下山每小时走,求小明家到山顶的路程.”小李查看解答时发现答案中的方程组中有污损:则答案中另一个方程应为( )
A. B.
C. D.
7.已知甲、乙两数之和是42,甲数的3倍等于乙数的4倍,求甲、乙两数.若设甲数为x,乙数为y,由题意得方程组( )
A. B.
C. D.
8.现有一段长为5000米的马路需要整修,由甲、乙两个工程小组先后接力完成,甲工程小组每天整修200米,乙工程小组每天整修250米,共用时22天.设甲工程小组整修马路米,乙工程小组整修马路米,依题意可列方程组( )
A. B.
C. D.
9.2023年杭州亚运会期间,吉祥物琼琼、宸宸、莲莲因其灵动可爱的形象受到了大家的喜爱.为了提高销量,某店家推出了吉祥物套装礼盒,一个套装礼盒里包含1个吉祥物宸宸玩偶和2个其他吉祥物的钥匙扣.已知一个玩偶的进价为60元,一个钥匙扣的进价为20元,该店家计划用5000元购进一批玩偶和钥匙扣,使得刚好配套,设购进x个玩偶,y个钥匙扣,则下列方程组正确的是( )
A. B.
C. D.
10.将浓度为的酒精与浓度为的酒精混合,制成了浓度为的酒精,设浓度为的酒精需要,浓度为的酒精需要,则列出的方程组为( )
A. B.
C. D.
填空题
11. 如图是由7个形状、大小都相同的小长方形和阴影部分无缝隙拼合而成的一个大长方形,则图中阴影部分的面积为 .
12.一个两位数,个位上的数比十位上的数的2倍多1,若将十位数字与个位数字调换位置,则比原两位数的2倍还多2,则原两位数是。
13.上学年初一某班的学生都是两人一桌,其中男生与女生同桌,这些女生占全班女生的.本学年该班新转入4个男生后,男女生刚好一样多.设上学年该班有男生x人,女生y人,则列方程组为 .
14.端午节时,王老师用72元钱买了荷包和五彩绳共20个(条),其中荷包每个4元,五彩绳每条3元,设王老师购买荷包x个,五彩绳y条,根据题意,列出的方程组是________.
15.已知点沿x轴正方向向右上方做跳马运动(即中国象棋“日”字型跳跃).若跳到位置,称为做一次“正横跳马”;若跳到位置,称为做一次“正竖跳马”,当点P连续做了a次“正横跳马”和b次“正竖跳马”后,到达点,则的值是 .
三、解答题
16.某长甲车间人数比乙车间人数的还少30人,如果从乙车间调10人到甲车间,那么甲车间的人数是乙车间的,求两个车间原来各有多少人?
17.一批货物要运往某地,货主准备租用汽运公司的甲、乙两种货车.已知最近两次租用这两种货车运货的情况如下表:
甲货车辆数 乙货车辆数 累计运货吨数
第一次 3 4 54
第二次 2 3 39
(1)1辆甲货车和1辆乙货车一次分别运货多少吨?
(2)若货主现有45t货物,计划同时租用甲货车a辆,乙货车b辆(a,b均为正整数),一次运完,且恰好每辆车都装满货物.请你帮助货主设计租车方案.
18.2023上海国际车展于2023年4月18日正式开幕,新能源汽车成为本次车展的亮点.某汽车销售公司计划购进一批新能源汽车尝试进行销售,据了解1辆A型新能源汽车、3辆B型新能源汽车的进价共计55万元;4辆A型新能源汽车、2辆B型新能源汽车的进价共计120万元.
(1)求A、B两种型号的新能源汽车每辆的进价分别为多少万元;
(2)若该公司计划正好用200万元购进以上两种型号的新能源汽车(两种型号的新能源汽车均购买),请你通过计算帮该公司求出全部的购买方案.
(一)课后反思:
本节课我学会了:
本节课存在的问题:
把本节课所学知识画出思维导图
参考答案
1.【答案】A
【分析】本题主要考查了从实际问题中抽象出二元一次方程组,设木头长为x尺,绳子长为y尺,根据用一根绳子去量一根木头的长、绳子还剩余尺,可得,根据将绳子对折再量木头,则木头还剩余1尺可得,据此列出方程组即可.
【详解】解;设木头长为x尺,绳子长为y尺,
由题意得,,
故选A.
【答案】B
【解析】略
3.【答案】C
【分析】本题主要考查了二元一次方程组的错解问题,解题的关键是理解题意得出正确的方程组.把甲的结果代入方程组两方程中,乙的结果代入第一个方程中,分别求出a,b,c的值,即可求出所求.
【详解】解:解:把代入方程组得: ,
把代入得:,
联立得:,解得:,
由,得到,
故选:C.
4.【答案】D
【分析】此题主要考查了由实际问题抽象出二元一次方程组,解题的关键是正确理解题意,抓住关键语句,找出等量关系.
根据题意可得等量关系:①甲商品数量+乙商品数量=30件;②甲商品的总价+乙商品的总价=400,然后列出方程组即可.
【详解】解:设买了甲种奖品件,乙种奖品件,依题意得:
,
故选:D
【答案】D
【解析】略
6.【答案】D
【解析】略
7.【答案】B
【解析】略
8.【答案】C
【分析】本题考查了二元一次方程组的实际应用,找准等量关系,正确列出二元一次方程组是解答本题的关键.
根据题意,找到两个等量关系:甲工程小组整修马路的长度乙工程小组整修马路的长度米,甲工程小组整修马路的天数乙工程小组整修马路的天数天,由此列出方程组,得到答案.
【详解】解:根据题意,
设甲工程小组整修马路米,乙工程小组整修马路米,
依题意可列方程组:
,
故选:.
9.【答案】C
【分析】本题考查了由实际问题抽象出二元一次方程组,利用总价单价数量,结合购进玩偶和钥匙扣数量间的关系,即可列出关于x,y的二元一次方程组,此题得解.找准等量关系,正确列出二元一次方程组是解题的关键.
【详解】解:∵一个套装礼盒里包含1个吉祥物宸宸玩偶和2个其他吉祥物的钥匙扣,
∴购进钥匙扣的数量是购进宸宸玩偶数量的2倍,
∴;
∵一个玩偶的进价为60元,一个钥匙扣的进价为20元,且店家共花费5000元,
∴.
根据题意可列出方程组.
故选:C.
10.【答案】C
【分析】本题考查列二元一次方程组解决实际问题,能够根据题意找出等量关系,并根据等量关系列出方程组是解决本题的关键.
【详解】解:的酒精质量加上浓度为的酒精质量等于,
的酒精中酒精质量加上浓度为的酒精中酒精质量等于混合后的液体中所含的酒精质量,
由此可知方程组为,
故选:C.
11.【答案】36
【分析】本题考查了二元一次方程组的应用,设小长方形的长为x,宽为y,则小正方形的边长为,根据图中各边之间的关系列出关于x,y的二元一次方程组,解之即可得出x,y的值,再利用正方形的面积公式计算即可.找准等量关系,正确列出二元一次方程组是解题的关键.
【详解】解:设小长方形的长为x,宽为y,则小正方形的边长为,
依题意得:,解得:,
∴图中阴影部分的面积为.
故答案为36.
【答案】25
【解析】略
13.【答案】
【分析】本题考查由实际问题抽象出二元一次方程组.根据本学年该班新转入4个男生后,男女生刚好一样多,其中男生与女生同桌,这些女生占全班女生的,可以列出相应的方程组.
【详解】解:由题意可得,
,
故答案为:.
14.【答案】14,6
【解析】略
15.【答案】
【分析】此题考查了点的坐标以及二元一次方程组的应用,读懂题意,正确列出方程组是解题的关键.由题意可得:做一次“正横跳马”横坐标增加2,纵坐标增加1,做一次“正竖跳马”横坐标增加1,纵坐标增加2,据此列方程组进行求解即可.
【详解】解:由题意,当点先连续做了a次“正横跳马”,再连续做b次“正竖跳马”后,到达点,则:
,
,得:,
∴;
故答案为:.
16.设甲车间有人,乙车间有人,根据题意,得
解得
答:甲车间有170人,乙车间有250人。
17.【答案】(1)1辆甲货车一次运货6t,1辆乙货车一次运货9t
(2)有2种租车方案.方案1:租用3辆甲货车,3辆乙货车;方案2:租用6辆甲货车,1辆乙货车
【详解】解:(1)设1辆甲货车一次运货xt,1辆乙货车一次运货yt.
根据题意,得解得
故1辆甲货车一次运货6t,1辆乙货车一次运货9t.
(2)根据题意,得,.
又a,b均为正整数,或
有2种租车方案.方案1:租用3辆甲货车,3辆乙货车;方案2:租用6辆甲货车,1辆乙货车.
18.【答案】(1)A、B两种型号的汽车每辆进价分别为25万元和10万元
(2)购买A型号汽车2辆,B型号汽车15辆;购买A型号汽车4辆,B型号汽车10辆;购买A型号汽车6辆,B型号汽车5辆.
【分析】本题主要考查了二元一次方程组的应用,解题的关键是根据等量关系列出方程,准确解方程.
(1)设A、B两种型号的汽车每辆进价分别为x万元,y万元,根据1辆A型新能源汽车、3辆B型新能源汽车的进价共计55万元;4辆A型新能源汽车、2辆B型新能源汽车的进价共计120万元列出方程组,解方程组即可;
(2)设购进A型号汽车m辆,B型号汽车n辆,根据该公司计划正好用200万元购进以上两种型号的新能源汽车,列出二元一次方程,根据、n为正整数,求出方程的解,得出结果即可.
【详解】(1)解:设A、B两种型号的汽车每辆进价分别为x万元,y万元,根据题意得:
,
解得:,
答:A、B两种型号的汽车每辆进价分别为25万元和10万元;
(2)解:设购进A型号汽车m辆,B型号汽车n辆,根据题意得:
,
∴,
∵、n为正整数,
∴,,,
∴购买A型号汽车2辆,B型号汽车15辆;
购买A型号汽车4辆,B型号汽车10辆;
购买A型号汽车6辆,B型号汽车5辆.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
