1.5 弹性碰撞和非弹性碰撞 课件(共31张PPT)2024-2025学年高二下学期物理人教版(2019)选择性必修第一册
文档属性
| 名称 | 1.5 弹性碰撞和非弹性碰撞 课件(共31张PPT)2024-2025学年高二下学期物理人教版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-08-11 14:16:34 | ||
图片预览











文档简介
(共31张PPT)
第一章 动量守恒定律
1.5 弹性碰撞和非弹性碰撞
根据上节课的分析,物体碰撞时系统的动量守恒。这节课我们从能量的角度研究碰撞前后物体动能的变化情况:进而对碰撞进行分类。
一、 弹性碰撞和非弹性碰撞
研究小车碰撞前后动能的变化
在本章第一节图1.1-2所示的实验中,经过计算我们知道,如果碰撞后两辆小车粘在一起,则总动能减少。这种情况普遍吗 是否有碰撞前后总动能不变的情况呢
实验
我们通过实验来研究这个问题。思考下面的问题也许有助于你设计实验。
·仔细观察图1.1-2的实验装置,想一想,总动能减少的原因是什么
·为了尽量减少总动能的损失,可以对图1.1-2的实验装置怎样进行改进 需要测量哪些实验数据 如何测量
在图1.5-1所示的实验装置中,分别为两辆小车安装了弹性碰撞架来减少动能的损失,你还有其他办法吗
如果系统在碰撞前后动能不变,这类碰撞叫作弹性碰撞(elastic collision)。如果系统在碰撞后动能减少,这类碰撞叫作非弹性碰撞(inelastic collision)。
钢球、玻璃球碰撞时,动能损失很小,它们的碰撞可以看作弹性碰撞;橡皮泥球之间的碰撞是非弹性碰撞。
按碰撞前后能量变化分类
例 题
如图1.5-2,在光滑水平面上,两个物体的质量都是 m,碰撞前一个物体静止,另一个以速度 v 向它撞去。碰撞后两个物体粘在一起,成为一个质量为 2m 的物体,以一定速度继续前进。碰撞后该系统的总动能是否会有损失
分析 可以先根据动量守恒定律求出碰撞后的共同速度 v′,然后分别计算碰撞前后的总动能进行比较。
解 根据动量守恒定律,2mv′=mv,则
v′=v
碰撞前的总动能 Ek=mv2
碰撞后的总动能 Ek′= (2m)v′2 = Ek
可见,碰撞后系统的总动能小于碰撞前系统的总动能。
那么,对于所有的碰撞,碰撞前后到底什么量会是不变的呢
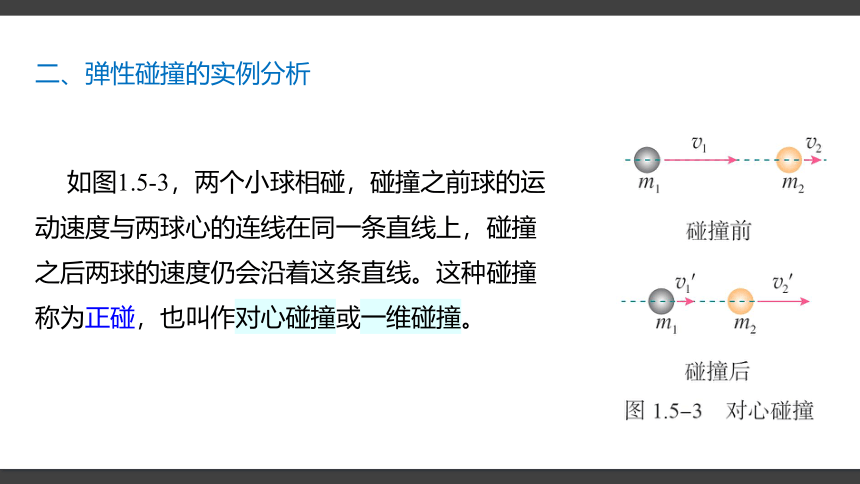
二、弹性碰撞的实例分析
如图1.5-3,两个小球相碰,碰撞之前球的运动速度与两球心的连线在同一条直线上,碰撞之后两球的速度仍会沿着这条直线。这种碰撞称为正碰,也叫作对心碰撞或一维碰撞。
下面我们分析一下,发生弹性碰撞的两个物体,由于质量不同,碰撞后的速度将有哪些特点。
为使研究问题简单,我们假设物体 m1 以速度 v1 与原来静止的物体 m2发生正碰,如图 1.5-4 所示。碰撞后它们的速度分别为 v1′和 v2′。
碰撞过程遵从动量守恒定律,据此可以列 出包含上述各已知量和未知量的方程
m1v1′+m2v2′=m1v1 (1)
弹性碰撞中没有动能损失,于是可以列出另一个方程
m1v1′2+m2v2′2=m1v12 (2)
从方程(1)(2)可以解出两个物体碰撞后的速度分别为
v1′= v1 (3)
v2′= v1 (4)
我们对几种情况下(3)(4)的结果作一些分析。
分析的方法之一是选取简单特例进行分析。如果所得的结论与实际情况一致,那么理论分析可能是正确的,否则一定出了问题。
● 若 m1=m2,这时有
m1-m2=0,m1+m2=2m1。根据 (3) (4)两式,得
v1′= 0
v2′=v1
这表示第一个物体的速度由 v1 变为0,而第二个物体由静止开始运动,运动的速度等于第一个物体原来的速度。
第3节“问题”中提到的冰壶的碰撞就属于这类情况。
● 若 m1>>m2,这时有
m1-m2≈m1,m1+m2≈m1。根据 (3) (4)两式,得
v1′= v1
v2′=2v1
这表示碰撞后,第一个物体的速度几乎没有改变,而第二个物体以 2v1,的速度被撞出去。
● 若 m1<<m2,这时有
m1-m2≈-m2,≈0。根据 (3) (4)两式,得
v1′=-v1
v2′=0
这表示碰撞以后,第一个物体被弹了回去,以原来的速率向反方向运动,而第二个物体仍然静止。
如果用乒乓球撞击保龄球,那么就会出现这种现象:保龄球保持静止,而乒乓球以大致相同的速率被弹回。
抽象与概括
物理概念是运用抽象、概括等方法进行思维加工的产物。
为了揭示事物的本质和规律,往往需要根据研究对象和问题的特点,从研究的目的出发,忽略个别的、非本质的属性,抽取共同的、本质的属性进行研究,这是一种抽象的思维方法。把一类事物共同的、本质的属性提炼出来,从而推广到同类事物上去,找到事物的共同属性,这是一种概括的思维方法。
科学方法
在动量概念的建立过程中,物理学家研究了各种各样的碰撞现象,寻找物理量来揭示运动的本质,发现:“每个物体所具有的‘动量’在碰撞后可以增多或减少,但是在碰撞前后系统的这一量值却保持不变。”科学前辈就是在追寻不变量的努力中通过抽象、概括等方法提出了动量的概念,并通过动量守恒定律建立了自然界的相互联系。
1. 在气垫导轨上,一个质量为 400g 的滑块以 15 cm/s 的速度与另一个质量为 200g、速度为 10cm/s 并沿相反方向运动的滑块迎面相撞,碰撞后两个滑块粘在一起。
(1) 求碰撞后滑块速度的大小和方向。
解:规定质量为 400g 的滑块碰撞前的速度方向为正方向,
由动量守恒定律得 m1v1-m2v2=(m1+m2)v′
解得 v′==m/s = 6.67×10-2 m/s,方向与质量为 400g 的滑块的初速度方向相同.
学以致用-提高练习
解:碰前两滑块的动能分别为
Ek1=m1v12= ×0.4×0.152 J = 4.50×10-3 J
Ek2= m2v22=2×0.2×0.12J=1.0×10-3 J
碰后两滑块的总动能为 Ek= (m1+m2)v′2= 1.35×10-3 J
则碰撞过程中,两滑块损失的机械能为 Ek=Ek1+Ek2-Ek=4.15×10-3J.
(2) 这次碰撞,两个滑块共损失了多少机械能
2. 速度为 10 m/s 的塑料球与静止的钢球发生正碰,钢球的质量是塑料球的4倍,碰撞是弹性的,求碰撞后两球的速度。
解:设塑料球的质量为 m,钢球质量为 M,且 M=4m,规定以塑料球碰前速度方向为正方向,由动量守恒定律及机械能守恒定律得
mv0=mv1+Mv2,mv02 = mv12+Mv22
解得 v1= v0=-v0=-6 m/s,方向与规定的正方向相反;
v2=v0=v0=4 m/s,方向与规定的正方向相同.
3. 有些核反应堆里要让中子与原子核碰撞以便把中子的速度降下来。为此,应该选用质量较大的还是质量较小的原子核 为什么
解:中子与原子核发生弹性正碰,同上述第2题,
有中子碰撞后速度 v′= v0
要使中子减速,设原子核质量为 M=nm (n为正整数),
那么有 v′=v0,
负号表示中子与原子核碰撞后速度 v 的方向与碰撞前的速度方向相反.可见 n 越小,越小. 即原子核质量越小,中子速度越容易降下来.
因此,应选用质量较小的原子核.
4.一种未知粒子跟静止的氢原子核正碰测出碰撞后氢原子核的速度是3.3×107m/s。该未知粒子跟静止的氮原子核正碰时,测出碰撞后氮原子核的速度是 4.4×106 m/s。已知氢原子核的质量是 mH,氮原子核的质量是14mH,上述碰撞都是弹性碰撞,求未知粒子的质量。
这实际是历史上查德威克通过测量质量从而发现中子的实验,请你根据以上查德威克的实验数据计算:中子的质量与氢核的质量 m 有什么关系
解:设未知粒子质量为 mx,与氢原子核发生正碰,
有 mxv0=mxv1+mHvH,mxv02=mxv12+mHvH2
解得 vH=v0
同理,未知粒子与氮原子核发生正碰,有 vN=v0
解得 =
已知 mN=14mH,故 mx=mH
即未知粒子质量跟氢原子核质量相等,这个未知粒子就是后来发现的中子,可见,中子质量跟氢原子核质量相等.
5. 质量为 m、速度为 v 的 A 球跟质量为 3m 的静止 B 球发生正碰。碰撞可能是弹性的也可能是非弹性的,因此,碰撞后 B 球的速度可能有不同的值。请你论证:碰撞后 B 球的速度可能是以下值吗
(1) 0.6v;(2) 0.4v。
解:A 球与 B 球发生正碰,若为弹性碰撞,
则有 mv=mvA+3mvB,mv2 = mvA2+ ·3mvB2,解得 vB= v=v.若为非弹性碰撞且机械能损失最大,则有 mv=(m+3m)vB,解得 vB=v.可见,B 球碰后速度的可能值的范围是 0.25v≤vB≤0.5v,
那么 vB 的值可能为 0.4v,不可能为 0.6v.
第一章 动量守恒定律
1.5 弹性碰撞和非弹性碰撞
根据上节课的分析,物体碰撞时系统的动量守恒。这节课我们从能量的角度研究碰撞前后物体动能的变化情况:进而对碰撞进行分类。
一、 弹性碰撞和非弹性碰撞
研究小车碰撞前后动能的变化
在本章第一节图1.1-2所示的实验中,经过计算我们知道,如果碰撞后两辆小车粘在一起,则总动能减少。这种情况普遍吗 是否有碰撞前后总动能不变的情况呢
实验
我们通过实验来研究这个问题。思考下面的问题也许有助于你设计实验。
·仔细观察图1.1-2的实验装置,想一想,总动能减少的原因是什么
·为了尽量减少总动能的损失,可以对图1.1-2的实验装置怎样进行改进 需要测量哪些实验数据 如何测量
在图1.5-1所示的实验装置中,分别为两辆小车安装了弹性碰撞架来减少动能的损失,你还有其他办法吗
如果系统在碰撞前后动能不变,这类碰撞叫作弹性碰撞(elastic collision)。如果系统在碰撞后动能减少,这类碰撞叫作非弹性碰撞(inelastic collision)。
钢球、玻璃球碰撞时,动能损失很小,它们的碰撞可以看作弹性碰撞;橡皮泥球之间的碰撞是非弹性碰撞。
按碰撞前后能量变化分类
例 题
如图1.5-2,在光滑水平面上,两个物体的质量都是 m,碰撞前一个物体静止,另一个以速度 v 向它撞去。碰撞后两个物体粘在一起,成为一个质量为 2m 的物体,以一定速度继续前进。碰撞后该系统的总动能是否会有损失
分析 可以先根据动量守恒定律求出碰撞后的共同速度 v′,然后分别计算碰撞前后的总动能进行比较。
解 根据动量守恒定律,2mv′=mv,则
v′=v
碰撞前的总动能 Ek=mv2
碰撞后的总动能 Ek′= (2m)v′2 = Ek
可见,碰撞后系统的总动能小于碰撞前系统的总动能。
那么,对于所有的碰撞,碰撞前后到底什么量会是不变的呢
二、弹性碰撞的实例分析
如图1.5-3,两个小球相碰,碰撞之前球的运动速度与两球心的连线在同一条直线上,碰撞之后两球的速度仍会沿着这条直线。这种碰撞称为正碰,也叫作对心碰撞或一维碰撞。
下面我们分析一下,发生弹性碰撞的两个物体,由于质量不同,碰撞后的速度将有哪些特点。
为使研究问题简单,我们假设物体 m1 以速度 v1 与原来静止的物体 m2发生正碰,如图 1.5-4 所示。碰撞后它们的速度分别为 v1′和 v2′。
碰撞过程遵从动量守恒定律,据此可以列 出包含上述各已知量和未知量的方程
m1v1′+m2v2′=m1v1 (1)
弹性碰撞中没有动能损失,于是可以列出另一个方程
m1v1′2+m2v2′2=m1v12 (2)
从方程(1)(2)可以解出两个物体碰撞后的速度分别为
v1′= v1 (3)
v2′= v1 (4)
我们对几种情况下(3)(4)的结果作一些分析。
分析的方法之一是选取简单特例进行分析。如果所得的结论与实际情况一致,那么理论分析可能是正确的,否则一定出了问题。
● 若 m1=m2,这时有
m1-m2=0,m1+m2=2m1。根据 (3) (4)两式,得
v1′= 0
v2′=v1
这表示第一个物体的速度由 v1 变为0,而第二个物体由静止开始运动,运动的速度等于第一个物体原来的速度。
第3节“问题”中提到的冰壶的碰撞就属于这类情况。
● 若 m1>>m2,这时有
m1-m2≈m1,m1+m2≈m1。根据 (3) (4)两式,得
v1′= v1
v2′=2v1
这表示碰撞后,第一个物体的速度几乎没有改变,而第二个物体以 2v1,的速度被撞出去。
● 若 m1<<m2,这时有
m1-m2≈-m2,≈0。根据 (3) (4)两式,得
v1′=-v1
v2′=0
这表示碰撞以后,第一个物体被弹了回去,以原来的速率向反方向运动,而第二个物体仍然静止。
如果用乒乓球撞击保龄球,那么就会出现这种现象:保龄球保持静止,而乒乓球以大致相同的速率被弹回。
抽象与概括
物理概念是运用抽象、概括等方法进行思维加工的产物。
为了揭示事物的本质和规律,往往需要根据研究对象和问题的特点,从研究的目的出发,忽略个别的、非本质的属性,抽取共同的、本质的属性进行研究,这是一种抽象的思维方法。把一类事物共同的、本质的属性提炼出来,从而推广到同类事物上去,找到事物的共同属性,这是一种概括的思维方法。
科学方法
在动量概念的建立过程中,物理学家研究了各种各样的碰撞现象,寻找物理量来揭示运动的本质,发现:“每个物体所具有的‘动量’在碰撞后可以增多或减少,但是在碰撞前后系统的这一量值却保持不变。”科学前辈就是在追寻不变量的努力中通过抽象、概括等方法提出了动量的概念,并通过动量守恒定律建立了自然界的相互联系。
1. 在气垫导轨上,一个质量为 400g 的滑块以 15 cm/s 的速度与另一个质量为 200g、速度为 10cm/s 并沿相反方向运动的滑块迎面相撞,碰撞后两个滑块粘在一起。
(1) 求碰撞后滑块速度的大小和方向。
解:规定质量为 400g 的滑块碰撞前的速度方向为正方向,
由动量守恒定律得 m1v1-m2v2=(m1+m2)v′
解得 v′==m/s = 6.67×10-2 m/s,方向与质量为 400g 的滑块的初速度方向相同.
学以致用-提高练习
解:碰前两滑块的动能分别为
Ek1=m1v12= ×0.4×0.152 J = 4.50×10-3 J
Ek2= m2v22=2×0.2×0.12J=1.0×10-3 J
碰后两滑块的总动能为 Ek= (m1+m2)v′2= 1.35×10-3 J
则碰撞过程中,两滑块损失的机械能为 Ek=Ek1+Ek2-Ek=4.15×10-3J.
(2) 这次碰撞,两个滑块共损失了多少机械能
2. 速度为 10 m/s 的塑料球与静止的钢球发生正碰,钢球的质量是塑料球的4倍,碰撞是弹性的,求碰撞后两球的速度。
解:设塑料球的质量为 m,钢球质量为 M,且 M=4m,规定以塑料球碰前速度方向为正方向,由动量守恒定律及机械能守恒定律得
mv0=mv1+Mv2,mv02 = mv12+Mv22
解得 v1= v0=-v0=-6 m/s,方向与规定的正方向相反;
v2=v0=v0=4 m/s,方向与规定的正方向相同.
3. 有些核反应堆里要让中子与原子核碰撞以便把中子的速度降下来。为此,应该选用质量较大的还是质量较小的原子核 为什么
解:中子与原子核发生弹性正碰,同上述第2题,
有中子碰撞后速度 v′= v0
要使中子减速,设原子核质量为 M=nm (n为正整数),
那么有 v′=v0,
负号表示中子与原子核碰撞后速度 v 的方向与碰撞前的速度方向相反.可见 n 越小,越小. 即原子核质量越小,中子速度越容易降下来.
因此,应选用质量较小的原子核.
4.一种未知粒子跟静止的氢原子核正碰测出碰撞后氢原子核的速度是3.3×107m/s。该未知粒子跟静止的氮原子核正碰时,测出碰撞后氮原子核的速度是 4.4×106 m/s。已知氢原子核的质量是 mH,氮原子核的质量是14mH,上述碰撞都是弹性碰撞,求未知粒子的质量。
这实际是历史上查德威克通过测量质量从而发现中子的实验,请你根据以上查德威克的实验数据计算:中子的质量与氢核的质量 m 有什么关系
解:设未知粒子质量为 mx,与氢原子核发生正碰,
有 mxv0=mxv1+mHvH,mxv02=mxv12+mHvH2
解得 vH=v0
同理,未知粒子与氮原子核发生正碰,有 vN=v0
解得 =
已知 mN=14mH,故 mx=mH
即未知粒子质量跟氢原子核质量相等,这个未知粒子就是后来发现的中子,可见,中子质量跟氢原子核质量相等.
5. 质量为 m、速度为 v 的 A 球跟质量为 3m 的静止 B 球发生正碰。碰撞可能是弹性的也可能是非弹性的,因此,碰撞后 B 球的速度可能有不同的值。请你论证:碰撞后 B 球的速度可能是以下值吗
(1) 0.6v;(2) 0.4v。
解:A 球与 B 球发生正碰,若为弹性碰撞,
则有 mv=mvA+3mvB,mv2 = mvA2+ ·3mvB2,解得 vB= v=v.若为非弹性碰撞且机械能损失最大,则有 mv=(m+3m)vB,解得 vB=v.可见,B 球碰后速度的可能值的范围是 0.25v≤vB≤0.5v,
那么 vB 的值可能为 0.4v,不可能为 0.6v.
