1.1 动量 课件-2024-2025学年高二下学期物理人教版(2019)选择性必修第一册(共32张PPT)
文档属性
| 名称 | 1.1 动量 课件-2024-2025学年高二下学期物理人教版(2019)选择性必修第一册(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-08-11 14:59:36 | ||
图片预览











文档简介
(共32张PPT)
1.1 动量
第一章 动量守恒定律
台球的碰撞、微观粒子的散射,这些运动似乎有天壤之别。然而,物理学的研究表明,它们遵从相同的科学规律——动量守恒定律。动量守恒定律是自然界中最普遍的规律之一,无论是设计火箭还是研究微观粒子,都离不开它.
从历史上看,一般说来,这(引入新的概念)永远是走向科学进步的最有力的方法之一。
——霍耳顿
霍耳顿(Gerald Holton,1922—),美国著名科学史家,哈佛大学物理学教授兼科学史教授。
从实验的现象似乎可以得出:碰撞后,A 球的速度大小不变地“传给”了 B 球。这意味着,碰撞前后,两球速度之和是不变的。那么所有的碰撞都有这样的规律吗
一、 寻求碰撞中的不变量
质量不同小球的碰撞
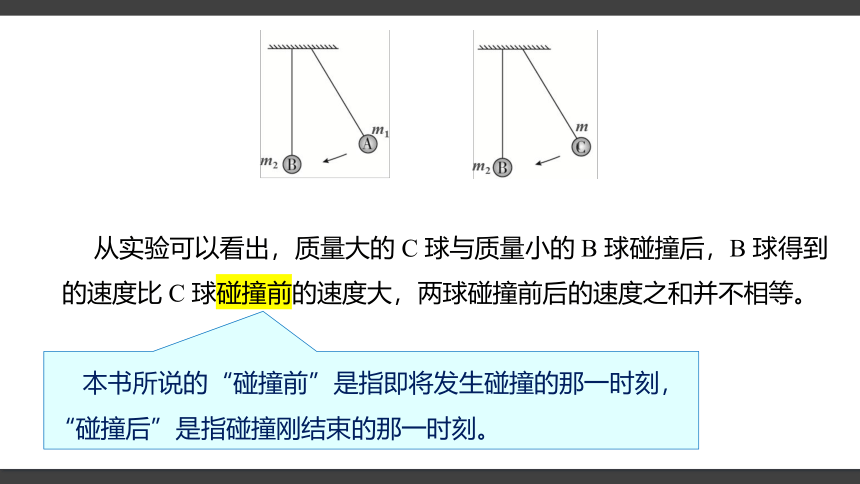
如图1.1—1,将上面实验中的A球换成大小相同的C球使C球质量大于B球质量,用手拉起C球至某一高度后放开,撞击静止的B球。我们可以看到,碰撞后B球获得较大的速度,摆起的最大高度大于C球被拉起时的高度。
从实验可以看出,质量大的 C 球与质量小的 B 球碰撞后,B 球得到的速度比 C 球碰撞前的速度大,两球碰撞前后的速度之和并不相等。
本书所说的“碰撞前”是指即将发生碰撞的那一时刻,“碰撞后”是指碰撞刚结束的那一时刻。
仔细观察你会发现,两球碰撞前后的速度变化跟它们的质量有关系。质量大、速度较小的C球,使质量小的B球获得了较大的速度。对于图1.1-1所示实验的现象,可能有的同学会猜想,两个物体碰撞前后动能之和不变,所以质量小的球速度大;也有的同学会猜想,两个物体碰撞前后速度与质量的乘积之和可能是不变的………
那么,对于所有的碰撞,碰撞前后到底什么量会是不变的呢
下面我们通过分析实验数据来研究上述问题。
实验如图1.1-2,两辆小车都放在滑轨上,用一辆运动的小车碰撞一辆静止的小车,碰撞后两辆小车粘在一起运动。小车的速度用滑轨上的数字计时器测量。下表中的数据是某次实验时采集的。其中,m1是运动小车的质量,m2是静止小车的质量;v是运动小车碰撞前的速度,v′ 是碰撞后两辆小车的共同速度。
m1/kg m2/kg v/(m·s-1) v′/(m·s-1)
1 0.519 0.519 0.628 0.307
2 0.519 0.718 0.656 0.265
3 0.718 0.519 0.572 0.321
表 两辆小车的质量和碰撞前后的速度
请你根据表中的数据,计算两辆小车碰撞前后的动能比较此实验中两辆小车碰撞前后动能之和是否不变。再计算两辆小车碰撞前后质量与速度的乘积,比较两辆小车碰撞前后质量与速度的乘积之和是否不变。
猜想:物体的质量和速度在碰撞前后有什么不变的关系
从实验的数据可以看出,此实验中两辆小车碰撞前后动能之和并不相等,但是质量与速度的乘积之和却基本不变。
二、 动量
上面的实验提示我们,对于发生碰撞的两个物体来说它们的 mv 之和在碰撞前后可能是不变的。这使我们意识到,mv 这个物理量具有特别的意义。
1、动量
物理学中把质量和速度的乘积 mv 定义为物体的动量,用字母 p 表示.
1)定义:
2)公式:
3)单位:
4)矢量:
p=mv
动量的单位是由质量的单位与速度的单位构成的,是千克米每秒,符号是 kg·m/s .
动量是矢量,动量的方向与速度的方向相同.
2、动量的变化
1) m,v 的大小和方向,三者任意一个变化,p就变。
2) Δp=p-p0=mv-mv0 (规定正方向)
3、动量与动能的区别
1) 动量 p=mv 是矢量,动能 Ek=mv2 是标量。
2) p 与 Ek 都是状态量,对应某一位置或某一时刻。
3) p 与 Ek 数值关系。
4、对动量的理解
是状态量
(2) 瞬时性:
(1) 矢量性:
运算遵循平行四边形定则
(3) 相对性:
物体的动量与参考系的选择有关
(4) Ek 发生变化,p 一定变化,但 p 变化,Ek 不一定变化。
速度相同
动能相同
动量相同
速度不相同
动能相同
动量不相同
例 题
一个质量为 0.1kg 的钢球,以 6m/s 的速度水平向右运动,碰到坚硬的壁后弹回,沿着同一直线以 6m/s 的速度水平向左运动 (图1.1-3)。碰撞前后钢球的动量变化了多少
分析 动量是矢量,虽然碰撞前后钢球速度的大小没有变化,但速度的方向变化了,所以动量的方向也发生了变化。为了求得钢球动量的变化量,需要先选定坐标轴的方向,确定碰撞前后钢球的动量,然后用碰撞后的动量减去碰撞前的动量求得动量的变化量。
解 取水平向右为坐标轴的方向。碰撞前钢球的速度为6ms,碰撞前钢球的动量为
p=mv=0.1×6 kg·m/s=0.6kg·m/s
碰撞后钢球的速度 v′=-6m/s,碰撞后钢球的动量为
p′=mv′=-0.1×6kg·m/s=-0.6 kg·m/s
碰撞前后钢球动量的变化量为
Δp=p′-p=(-0.6-0.6) kg·m/s=-1.2 kg·m/s
动量的变化量是矢量,求得的数值为负值,表示它的方向与坐标轴的方向相反,即 p 的方向水平向左。
让一位同学把一个充气到直径 1m 左右的大乳胶气球,以某一速度水平投向你,请你接住(图1.1-4)。把气放掉后气球变得很小,再把气球以相同的速度投向你。两种情况下,你的体验有什么不同 这是为什么呢
做一做
1. 解答以下三个问题,总结动量与动能概念的不同。
(1) 质量为 2kg 的物体,速度由 3m/s 增大为 6m/s,它的动量和动能各增大为原来的几倍
(2) 质量为 2kg 的物体,速度由向东的3 m/s变为向西的 3m/s,它的动量和动能是否发生变化 如果发生变化,变化量各是多少
(3) A物体质量是 2kg,速度是 3m/s,方向向东;B物体质量是 3kg,速度是4m/s,方向向西。它们动量的失量和是多少 它们的动能之和是多少
学以致用-提高练习
解:质量为 2kg 的物体,速度由 3m/s 增大到6m/s,
则有 p1=mv1=6kg·m/s,p2=mv2=12kg·m/s
则 p2=2p1,即动量增大为原来的2倍.
Ek1=mv12= 9J,Ek2= mv22 = 36J
则 Ek2= 4Ek1,
即动能增大为原来的4倍.
(1) 质量为 2kg 的物体,速度由 3m/s 增大为 6m/s,它的动量和动能各增大为原来的几倍
(2) 质量为 2kg 的物体,速度由向东的3 m/s变为向西的 3m/s,它的动量和动能是否发生变化 如果发生变化,变化量各是多少
解:质量为2kg的物体,速度由向东的3m/s变为向西的3 m/s,规定向东为正方向,则有 p=mv2-mv1=[2×(-3)-2×3]kg·m/s=-12kg·m/s,负号表示方向向西.
Ek=mv22-mv12=0
故动量发生变化且变化量 p=-12kg·m/s,方向向西;
动能不改变.
(3) A物体质量是 2kg,速度是 3m/s,方向向东;B物体质量是 3kg,速度是4m/s,方向向西。它们动量的失量和是多少 它们的动能之和是多少
解:A物体质量为2kg,速度是3m/s,方向向东,B物体质量为3kg,速度是4m/s,方向向西,规定向东为正方向,
有 pA=mAvA=6kg·m/s,pB=mBvB=3×(-4) kg·m/s=12kg·m/s,
则动量的矢量和 pA+pB=-6kg·m/s,负号表示总动量方向向西.
EkA=mAvA2=9J,EkB= mBvB2=24J,
则总动能 EkA+EkB=33 J.
由以上三个问题可知,物体的动量是物体质量和速度的乘积,动量是矢量,方向与速度方向相同;物体的动能是物体质量与速度平方乘积的二分之一,是标量.
2. 一个质量为 2kg 的物体在合力 F 的作用下从静止开始沿直线运动。F 随时间 t 变化的图像如图 1.1-5 所示。
(1) t=2s 时物体的动量大小是多少
解:t1=2s 时,有 v1=a1t1,a1==1m/s2,
则 v1=2m/s
故物体的动量大小 p1=mv1=4 kg·m/s.
(2) t=3s 时物体的动量大小是多少
解:t2=3s 时,有 a2==-0.5 m/s2
则 t2=3s 时,
物体的速度 v2=v1+a2Δt
=2 m/s+(-0.5)×1 m/s
=1.5 m/s,
故物体的动量大小 p2=mv2=3 kg·m/s.
1.1 动量
第一章 动量守恒定律
台球的碰撞、微观粒子的散射,这些运动似乎有天壤之别。然而,物理学的研究表明,它们遵从相同的科学规律——动量守恒定律。动量守恒定律是自然界中最普遍的规律之一,无论是设计火箭还是研究微观粒子,都离不开它.
从历史上看,一般说来,这(引入新的概念)永远是走向科学进步的最有力的方法之一。
——霍耳顿
霍耳顿(Gerald Holton,1922—),美国著名科学史家,哈佛大学物理学教授兼科学史教授。
从实验的现象似乎可以得出:碰撞后,A 球的速度大小不变地“传给”了 B 球。这意味着,碰撞前后,两球速度之和是不变的。那么所有的碰撞都有这样的规律吗
一、 寻求碰撞中的不变量
质量不同小球的碰撞
如图1.1—1,将上面实验中的A球换成大小相同的C球使C球质量大于B球质量,用手拉起C球至某一高度后放开,撞击静止的B球。我们可以看到,碰撞后B球获得较大的速度,摆起的最大高度大于C球被拉起时的高度。
从实验可以看出,质量大的 C 球与质量小的 B 球碰撞后,B 球得到的速度比 C 球碰撞前的速度大,两球碰撞前后的速度之和并不相等。
本书所说的“碰撞前”是指即将发生碰撞的那一时刻,“碰撞后”是指碰撞刚结束的那一时刻。
仔细观察你会发现,两球碰撞前后的速度变化跟它们的质量有关系。质量大、速度较小的C球,使质量小的B球获得了较大的速度。对于图1.1-1所示实验的现象,可能有的同学会猜想,两个物体碰撞前后动能之和不变,所以质量小的球速度大;也有的同学会猜想,两个物体碰撞前后速度与质量的乘积之和可能是不变的………
那么,对于所有的碰撞,碰撞前后到底什么量会是不变的呢
下面我们通过分析实验数据来研究上述问题。
实验如图1.1-2,两辆小车都放在滑轨上,用一辆运动的小车碰撞一辆静止的小车,碰撞后两辆小车粘在一起运动。小车的速度用滑轨上的数字计时器测量。下表中的数据是某次实验时采集的。其中,m1是运动小车的质量,m2是静止小车的质量;v是运动小车碰撞前的速度,v′ 是碰撞后两辆小车的共同速度。
m1/kg m2/kg v/(m·s-1) v′/(m·s-1)
1 0.519 0.519 0.628 0.307
2 0.519 0.718 0.656 0.265
3 0.718 0.519 0.572 0.321
表 两辆小车的质量和碰撞前后的速度
请你根据表中的数据,计算两辆小车碰撞前后的动能比较此实验中两辆小车碰撞前后动能之和是否不变。再计算两辆小车碰撞前后质量与速度的乘积,比较两辆小车碰撞前后质量与速度的乘积之和是否不变。
猜想:物体的质量和速度在碰撞前后有什么不变的关系
从实验的数据可以看出,此实验中两辆小车碰撞前后动能之和并不相等,但是质量与速度的乘积之和却基本不变。
二、 动量
上面的实验提示我们,对于发生碰撞的两个物体来说它们的 mv 之和在碰撞前后可能是不变的。这使我们意识到,mv 这个物理量具有特别的意义。
1、动量
物理学中把质量和速度的乘积 mv 定义为物体的动量,用字母 p 表示.
1)定义:
2)公式:
3)单位:
4)矢量:
p=mv
动量的单位是由质量的单位与速度的单位构成的,是千克米每秒,符号是 kg·m/s .
动量是矢量,动量的方向与速度的方向相同.
2、动量的变化
1) m,v 的大小和方向,三者任意一个变化,p就变。
2) Δp=p-p0=mv-mv0 (规定正方向)
3、动量与动能的区别
1) 动量 p=mv 是矢量,动能 Ek=mv2 是标量。
2) p 与 Ek 都是状态量,对应某一位置或某一时刻。
3) p 与 Ek 数值关系。
4、对动量的理解
是状态量
(2) 瞬时性:
(1) 矢量性:
运算遵循平行四边形定则
(3) 相对性:
物体的动量与参考系的选择有关
(4) Ek 发生变化,p 一定变化,但 p 变化,Ek 不一定变化。
速度相同
动能相同
动量相同
速度不相同
动能相同
动量不相同
例 题
一个质量为 0.1kg 的钢球,以 6m/s 的速度水平向右运动,碰到坚硬的壁后弹回,沿着同一直线以 6m/s 的速度水平向左运动 (图1.1-3)。碰撞前后钢球的动量变化了多少
分析 动量是矢量,虽然碰撞前后钢球速度的大小没有变化,但速度的方向变化了,所以动量的方向也发生了变化。为了求得钢球动量的变化量,需要先选定坐标轴的方向,确定碰撞前后钢球的动量,然后用碰撞后的动量减去碰撞前的动量求得动量的变化量。
解 取水平向右为坐标轴的方向。碰撞前钢球的速度为6ms,碰撞前钢球的动量为
p=mv=0.1×6 kg·m/s=0.6kg·m/s
碰撞后钢球的速度 v′=-6m/s,碰撞后钢球的动量为
p′=mv′=-0.1×6kg·m/s=-0.6 kg·m/s
碰撞前后钢球动量的变化量为
Δp=p′-p=(-0.6-0.6) kg·m/s=-1.2 kg·m/s
动量的变化量是矢量,求得的数值为负值,表示它的方向与坐标轴的方向相反,即 p 的方向水平向左。
让一位同学把一个充气到直径 1m 左右的大乳胶气球,以某一速度水平投向你,请你接住(图1.1-4)。把气放掉后气球变得很小,再把气球以相同的速度投向你。两种情况下,你的体验有什么不同 这是为什么呢
做一做
1. 解答以下三个问题,总结动量与动能概念的不同。
(1) 质量为 2kg 的物体,速度由 3m/s 增大为 6m/s,它的动量和动能各增大为原来的几倍
(2) 质量为 2kg 的物体,速度由向东的3 m/s变为向西的 3m/s,它的动量和动能是否发生变化 如果发生变化,变化量各是多少
(3) A物体质量是 2kg,速度是 3m/s,方向向东;B物体质量是 3kg,速度是4m/s,方向向西。它们动量的失量和是多少 它们的动能之和是多少
学以致用-提高练习
解:质量为 2kg 的物体,速度由 3m/s 增大到6m/s,
则有 p1=mv1=6kg·m/s,p2=mv2=12kg·m/s
则 p2=2p1,即动量增大为原来的2倍.
Ek1=mv12= 9J,Ek2= mv22 = 36J
则 Ek2= 4Ek1,
即动能增大为原来的4倍.
(1) 质量为 2kg 的物体,速度由 3m/s 增大为 6m/s,它的动量和动能各增大为原来的几倍
(2) 质量为 2kg 的物体,速度由向东的3 m/s变为向西的 3m/s,它的动量和动能是否发生变化 如果发生变化,变化量各是多少
解:质量为2kg的物体,速度由向东的3m/s变为向西的3 m/s,规定向东为正方向,则有 p=mv2-mv1=[2×(-3)-2×3]kg·m/s=-12kg·m/s,负号表示方向向西.
Ek=mv22-mv12=0
故动量发生变化且变化量 p=-12kg·m/s,方向向西;
动能不改变.
(3) A物体质量是 2kg,速度是 3m/s,方向向东;B物体质量是 3kg,速度是4m/s,方向向西。它们动量的失量和是多少 它们的动能之和是多少
解:A物体质量为2kg,速度是3m/s,方向向东,B物体质量为3kg,速度是4m/s,方向向西,规定向东为正方向,
有 pA=mAvA=6kg·m/s,pB=mBvB=3×(-4) kg·m/s=12kg·m/s,
则动量的矢量和 pA+pB=-6kg·m/s,负号表示总动量方向向西.
EkA=mAvA2=9J,EkB= mBvB2=24J,
则总动能 EkA+EkB=33 J.
由以上三个问题可知,物体的动量是物体质量和速度的乘积,动量是矢量,方向与速度方向相同;物体的动能是物体质量与速度平方乘积的二分之一,是标量.
2. 一个质量为 2kg 的物体在合力 F 的作用下从静止开始沿直线运动。F 随时间 t 变化的图像如图 1.1-5 所示。
(1) t=2s 时物体的动量大小是多少
解:t1=2s 时,有 v1=a1t1,a1==1m/s2,
则 v1=2m/s
故物体的动量大小 p1=mv1=4 kg·m/s.
(2) t=3s 时物体的动量大小是多少
解:t2=3s 时,有 a2==-0.5 m/s2
则 t2=3s 时,
物体的速度 v2=v1+a2Δt
=2 m/s+(-0.5)×1 m/s
=1.5 m/s,
故物体的动量大小 p2=mv2=3 kg·m/s.
