22.3.3实际问题与二次函数 第3课时 二次函数与拱桥类问题【人教九上数学精彩课堂教案】
文档属性
| 名称 | 22.3.3实际问题与二次函数 第3课时 二次函数与拱桥类问题【人教九上数学精彩课堂教案】 |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-13 14:07:58 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
22.3 实际问题与二次函数
第3课时 二次函数与拱桥类问题
实际情境 置疑探究 归纳探究 复习探究 类比探究 悬念激趣
实际情境 (1)欣赏一组石拱桥的图片(如图22-3-14),观察桥拱的形状.这组石拱桥图案中,桥拱的形状和抛物线像吗 有关桥拱的问题可以用抛物线知识来解决吗
图22-3-14
(2)步行街广场中心处有高低不同的各种喷泉(如图22-3-15),喷泉喷出的水柱的形状和抛物线像吗 有关喷泉的问题可以用抛物线知识来解决吗
图22-3-15
[教学提示] 从学生生活中熟知的拱桥和喷泉问题引入新课,为学生能够积极主动地投入到探索活动创设情境,激发学生的学习热情,同时为探索二次函数的实际应用提供背景材料.让学生欣赏这一组图片以后,引入问题.从问题中提问学生你知道该抛物线的顶点是什么吗 与y轴的交点是什么 你能求出函数解析式吗
悬念激趣 如图22-3-16,一场篮球赛中,小明跳起投篮,已知球出手时离地面 米,与篮筐中心的水平距离为8米,当球出手后水平距离为4米时,达到最大高度4米.设篮球运动的轨迹为抛物线,篮筐中心距离地面3米.问此球能否投中
图22-3-16
[教学提示] 从学生熟知的体育活动入手,以如何才能投中为目标激起学生的学习欲望.先复习二次函数解析式的形式;再观察图象,从这些数据中提问学生你能得出抛物线的顶点坐标、与y轴的交点坐标吗 根据这些条件如何设二次函数的解析式 判断球能否投中可转化为点的坐标问题是什么意思
教材母题——第51页探究3
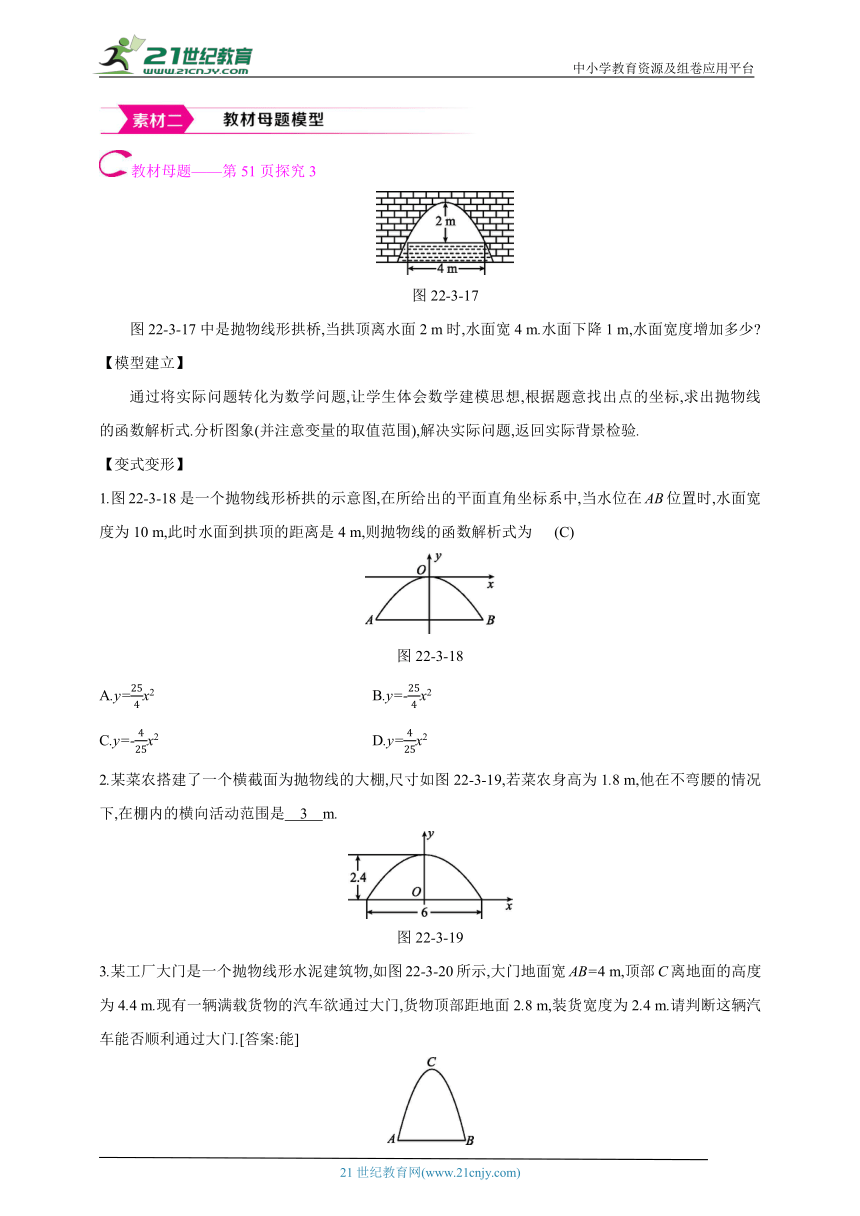
图22-3-17
图22-3-17中是抛物线形拱桥,当拱顶离水面2 m时,水面宽4 m.水面下降1 m,水面宽度增加多少
【模型建立】
通过将实际问题转化为数学问题,让学生体会数学建模思想,根据题意找出点的坐标,求出抛物线的函数解析式.分析图象(并注意变量的取值范围),解决实际问题,返回实际背景检验.
【变式变形】
1.图22-3-18是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在AB位置时,水面宽度为10 m,此时水面到拱顶的距离是4 m,则抛物线的函数解析式为 (C)
图22-3-18
A.y=x2 B.y=-x2
C.y=-x2 D.y=x2
2.某菜农搭建了一个横截面为抛物线的大棚,尺寸如图22-3-19,若菜农身高为1.8 m,他在不弯腰的情况下,在棚内的横向活动范围是 3 m.
图22-3-19
3.某工厂大门是一个抛物线形水泥建筑物,如图22-3-20所示,大门地面宽AB=4 m,顶部C离地面的高度为4.4 m.现有一辆满载货物的汽车欲通过大门,货物顶部距地面2.8 m,装货宽度为2.4 m.请判断这辆汽车能否顺利通过大门.[答案:能]
图22-3-20
4.如图22-3-21,有一抛物线形拱桥,已知水位在AB位置时,水面的宽度是4 米,水位上升4米就达到警戒线CD,这时水面的宽度是4 米.若洪水到来时,水位以每小时0.5米的速度上升,求水过警戒线后几小时淹到拱桥顶端M处.[答案:8小时]
图22-3-21
【评价角度1】 利用二次函数的性质解决抛物线形拱桥、隧道类、帐篷等问题
方法指引:此类问题常见题型是利用二次函数的性质解决抛物线形拱桥、隧道类、帐篷等问题,解决这类问题的关键是建立合适的平面直角坐标系,并且把相关数据转化为点的坐标,然后利用二次函数的知识解决问题.例如本课素材二[教材母题模型].
【评价角度2】 利用二次函数的性质解决刹车、投篮、喷水等其他实际问题
方法指引:利用二次函数还可以解决诸如刹车距离与时间问题、投篮、喷水等问题,这类问题一般难度不大.例如本课素材一[创设学习场景]中的悬念激趣.
【评价角度3】 二次函数压轴题
方法指引:1.图形运动问题:要注意用运动与变化的眼光去观察和研究图形,把握图形运动与变化的全过程,抓住其中的等量关系和变量关系,并特别关注一些不变的量、不变的关系或特殊关系,善于化动为静,由特殊情形(特殊点,特殊值,特殊位置,特殊图形等)逐步过渡到一般情形,综合运用各种相关知识及数形结合、分类讨论、转化等数学思想加以解决.当一个问题是确定有关图形的变量之间的关系时,通常建立函数模型或不等式模型求解;当确定图形之间的特殊位置关系或者一些特殊的值时,通常建立方程模型去求解.
2.存在性问题:二次函数常常与三角形、四边形和圆综合在一起运用,解决这类问题需要用到数形结合的数学思想,把“数”与“形”结合起来,互相渗透.存在探索型问题是指在给定条件下,判断某种数学现象是否存在、某个结论是否出现的问题.解决这类问题的一般思路是先假设结论的某一方面存在,然后在这个假设下进行演绎推理,若推出矛盾,则可否定假设;若推出合理结论,则可肯定假设.
课题 第3课时 二次函数与拱桥类问题 授课人
教 学 目 标 1.能根据具体的问题情境建立数学模型,应用二次函数的知识求解,并根据具体问题的实际意义检验结果的合理性. 2.学会从多个角度思考问题,逐步提高解决问题的能力. 3.通过对实际问题的研究,体会建模的数学思想. 4.经历将实际问题抽象为数学问题的过程,体会转化和数形结合的思想. 5.通过问题的设计、解答,使学生学会从不同角度寻求解决问题的方法,获得解决问题的经验. 6.通过小组合作交流,提高合作意识,培养创新精神. 7.通过用二次函数的知识解决实际问题,体会数学与现实生活的紧密联系,提高学习数学的兴趣,增强应用数学的意识.
教学 重点 探究应用二次函数的知识解决实际问题的方法.
教学 难点 如何从实际问题中抽象出数学问题,建立数学模型.
授课 类型 新授课 课时
教具 多媒体
教学活动
教学 步骤 师生活动 设计意图
回顾 1.二次函数解析式常见的形式有哪几种 说明其特征. 2.对二次函数y=ax2+bx+c的图象进行平移时: 向上平移k(k>0)个单位长度得到的图象对应的函数解析式是什么 向下平移k(k>0)个单位长度得到的图象对应的函数解析式是什么 向左平移h(h>0)个单位长度得到的图象对应的函数解析式是什么 向右平移h(h>0)个单位长度得到的图象对应的函数解析式是什么 师生活动:教师引导学生回忆知识,学生进行解答,教师做好点评. 在已有知识的基础上提出新的问题,能为学生营造一个主动思考、探索的氛围,激发学生的学习兴趣.
活动 一: 创设 情境 导入 新课 【课堂引入】 问题:图22-3-22是抛物线形拱桥,当拱顶离水面2米时,水面宽4米.若水面下降1米,则水面宽度将增加多少米 图22-3-22 师生活动: 教师进行引导,提出问题: 对于本题你认为应该运用什么知识进行解答 根据问题中的图形为抛物线,由此可知本题应该运用二次函数的知识进行解答. 学生分组讨论,如何利用函数模型解决问题,教师帮助学生解决问题. 通过日常生活中的实际问题,激发学生的学习兴趣,培养学生的探究意识和解决实际问题的能力.
活动 二: 探究 与 应用 1.探究新知 活动一:针对[课堂引入]的问题,教师进行提示: ①要解答二次函数的问题,必须把抛物线放在平面直角坐标系中,所以必须建立适当的平面直角坐标系; ②求水面增加的宽度,实际上就是求水面与抛物线的交点的坐标; ③求出函数解析式,进而求点的坐标; ④求函数解析式应该用待定系数法. 师生活动:学生先独立进行解答,然后小组内交流讨论,教师适时点拨,指导学生写出解题过程. 解:以抛物线的顶点为原点,对称轴为y轴,建立平面直角坐标系,如图22-3-23.根据图象的特殊性,设抛物线的函数解析式为y=ax2,由抛物线经过点A(-2,-2),可得a=-,所以抛物线的函数解析式为y=-x2.把y=-3代入函数解析式,得x=±,所以CD-AB=(2-4)米,则水面宽度将增加(2-4)米. 图22-3-23 活动二:教师指导学生建立不同的平面直角坐标系进行解答. 学生独立完成解题过程,小组内交流比较:建立的平面直角坐标系是否相同,计算结果是否一致. 如解法:如图22-3-24,设AB所在直线为x轴,经过AB的中点O且与AB垂直的直线为y轴,则通过画图可知O为原点,抛物线以y轴为对称轴,且经过A,B两点,可求出OA和OB的长为AB长的一半,即为2米,抛物线的顶点坐标为(0,2),通过以上条件可设解析式为顶点式y=ax2+2.将点A的坐标(-2,0)代入解析式,得a=-,所以抛物线的函数解析式为y=-x2+2.把y=-1代入上式,得x=±,所以CD-AB=米,则水面宽度将增加(2-4)米. 图22-3-24 2.归纳总结 教师引导学生进行归纳总结: ①建立适当的平面直角坐标系;②根据题意找出题目中的点的坐标;③求出抛物线的函数解析式;④直接利用图象解决实际问题. 1.通过建立不同的平面直角坐标系得到不同的函数解析式,但结果是相同的,选择合适的平面直角坐标系可以使解答更简便,更明确易懂. 2.通过总结抛物线形实际问题的解题步骤,使学生明确问题的解答方法,思路清晰,明确解题方向.
【应用举例】 例1 自动喷灌设备的喷流情况如图22-3-25所示,设水管AB在高出地面3.5米的B处有一自动旋转的喷水头,水流是抛物线形,喷头B与水流最高点C连线与地面成45°角,水流最高点C比喷头B高2米,求水流落点D到点A的距离. 师生活动:学生按要求进行解答,教师做好指导、点拨. 图22-3-25 教师关注: (1)学生能否熟练地运用二次函数的有关知识解决实际问题; (2)学生是否具有探索精神. 激发学生的学习欲望和兴趣,让学生切实感受到数学就在身边.让学生学会将获得的知识经验进行类比迁移,并让学生体验数学建模思想,增强应用意识.
活动 二: 探究 与 应用 【拓展提升】 例2 如图22-3-26,一场篮球赛中,小明跳起投篮,已知球出手时离地面米,与篮筐中心的水平距离为7米,当球出手后水平距离为4米时达到最大高度4米.设篮球运动的轨迹为抛物线,篮筐中心距离地面3.05米.此球能否投中篮筐 师生活动:学生独立解答,再合作交流,然后展示成果.教师巡视,观察学生解决问题的过程与方法,并给予学习有困难的学生及时的引导和帮助. 图22-3-26 通过抛物线与常见生活情景相联系的题目的展示,拓宽学生视野,提高学生灵活运用知识的能力.
活动 三: 课堂 总结 反思 【达标测评】 1.如图22-3-27所示的是一学生推铅球时铅球行进高度y(m)与水平距离x(m)之间的函数图象,观察图象,则铅球推出的水平距离是 10 m. 图22-3-27 2.小明以二次函数y=2x2-4x+8的图象为灵感为“北京房山国际葡萄酒大赛”设计了一款杯子,如图22-3-28为杯子的设计稿,若AB=4,DE=3,则杯子的高CE为 (B) 图22-3-28 A.14 B.11 C.6 D.3 3.某工厂的大门是一个抛物线形水泥建筑物,大门的地面宽度为8 m,两侧距地面3 m高处各有一盏壁灯,两盏壁灯之间的水平距离为6 m,如图22-3-29所示,则厂门的高约为 6.9 m (水泥建筑物厚度不计,精确到0.1 m). 图22-3-29 4.城市花园广场喷泉的喷嘴安装在平地上,有一喷嘴喷出的水流呈抛物线形,喷出水流的高度y(m)与喷出水流距喷嘴的水平距离x(m)之间满足函数解析式y=-x2+2x. (1)求喷嘴喷出的水流的最大高度是多少; (2)求喷嘴喷出的水流的最远距离是多少. 学生进行当堂检测,完成后,教师进行批阅、点评、讲解. 针对本课时的主要问题,从多个角度、分层次进行检测,达到学有所成、了解课堂学习效果的目的.
1.课堂总结: (1)你在本节课中有哪些收获 有哪些进步 (2)学习本节课后,还存在哪些困惑 2.布置作业: 教材第52页习题22.3第3题. 小结环节的设置能够让学生养成自主归纳课堂重点的习惯,提高学生的学习能力.
活动 三: 课堂 总结 反思 【知识网络】 提纲挈领,重点突出.
【教学反思】 ①[授课流程反思] 在探究新知环节中,充分利用多媒体手段提高课堂效率,激发学生的学习兴趣,调动学生的学习积极性,有效解决了教学的重难点;在课堂训练环节中,教师给予学生充分的自由时间,让学生能够体会建立平面直角坐标系的作用,明确解答问题的步骤,树立建模思想. ②[讲授效果反思] 教师强调重点:(1)明确解决抛物线形问题的步骤;(2)设抛物线的函数解析式时,要根据函数图象选择恰当的形式. ③[师生互动反思] 在开放、多样的教学活动中,培养学生主动合作的意识及对数学的兴趣和爱好. ④[习题反思] 好题题号 错题题号 反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
22.3 实际问题与二次函数
第3课时 二次函数与拱桥类问题
实际情境 置疑探究 归纳探究 复习探究 类比探究 悬念激趣
实际情境 (1)欣赏一组石拱桥的图片(如图22-3-14),观察桥拱的形状.这组石拱桥图案中,桥拱的形状和抛物线像吗 有关桥拱的问题可以用抛物线知识来解决吗
图22-3-14
(2)步行街广场中心处有高低不同的各种喷泉(如图22-3-15),喷泉喷出的水柱的形状和抛物线像吗 有关喷泉的问题可以用抛物线知识来解决吗
图22-3-15
[教学提示] 从学生生活中熟知的拱桥和喷泉问题引入新课,为学生能够积极主动地投入到探索活动创设情境,激发学生的学习热情,同时为探索二次函数的实际应用提供背景材料.让学生欣赏这一组图片以后,引入问题.从问题中提问学生你知道该抛物线的顶点是什么吗 与y轴的交点是什么 你能求出函数解析式吗
悬念激趣 如图22-3-16,一场篮球赛中,小明跳起投篮,已知球出手时离地面 米,与篮筐中心的水平距离为8米,当球出手后水平距离为4米时,达到最大高度4米.设篮球运动的轨迹为抛物线,篮筐中心距离地面3米.问此球能否投中
图22-3-16
[教学提示] 从学生熟知的体育活动入手,以如何才能投中为目标激起学生的学习欲望.先复习二次函数解析式的形式;再观察图象,从这些数据中提问学生你能得出抛物线的顶点坐标、与y轴的交点坐标吗 根据这些条件如何设二次函数的解析式 判断球能否投中可转化为点的坐标问题是什么意思
教材母题——第51页探究3
图22-3-17
图22-3-17中是抛物线形拱桥,当拱顶离水面2 m时,水面宽4 m.水面下降1 m,水面宽度增加多少
【模型建立】
通过将实际问题转化为数学问题,让学生体会数学建模思想,根据题意找出点的坐标,求出抛物线的函数解析式.分析图象(并注意变量的取值范围),解决实际问题,返回实际背景检验.
【变式变形】
1.图22-3-18是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在AB位置时,水面宽度为10 m,此时水面到拱顶的距离是4 m,则抛物线的函数解析式为 (C)
图22-3-18
A.y=x2 B.y=-x2
C.y=-x2 D.y=x2
2.某菜农搭建了一个横截面为抛物线的大棚,尺寸如图22-3-19,若菜农身高为1.8 m,他在不弯腰的情况下,在棚内的横向活动范围是 3 m.
图22-3-19
3.某工厂大门是一个抛物线形水泥建筑物,如图22-3-20所示,大门地面宽AB=4 m,顶部C离地面的高度为4.4 m.现有一辆满载货物的汽车欲通过大门,货物顶部距地面2.8 m,装货宽度为2.4 m.请判断这辆汽车能否顺利通过大门.[答案:能]
图22-3-20
4.如图22-3-21,有一抛物线形拱桥,已知水位在AB位置时,水面的宽度是4 米,水位上升4米就达到警戒线CD,这时水面的宽度是4 米.若洪水到来时,水位以每小时0.5米的速度上升,求水过警戒线后几小时淹到拱桥顶端M处.[答案:8小时]
图22-3-21
【评价角度1】 利用二次函数的性质解决抛物线形拱桥、隧道类、帐篷等问题
方法指引:此类问题常见题型是利用二次函数的性质解决抛物线形拱桥、隧道类、帐篷等问题,解决这类问题的关键是建立合适的平面直角坐标系,并且把相关数据转化为点的坐标,然后利用二次函数的知识解决问题.例如本课素材二[教材母题模型].
【评价角度2】 利用二次函数的性质解决刹车、投篮、喷水等其他实际问题
方法指引:利用二次函数还可以解决诸如刹车距离与时间问题、投篮、喷水等问题,这类问题一般难度不大.例如本课素材一[创设学习场景]中的悬念激趣.
【评价角度3】 二次函数压轴题
方法指引:1.图形运动问题:要注意用运动与变化的眼光去观察和研究图形,把握图形运动与变化的全过程,抓住其中的等量关系和变量关系,并特别关注一些不变的量、不变的关系或特殊关系,善于化动为静,由特殊情形(特殊点,特殊值,特殊位置,特殊图形等)逐步过渡到一般情形,综合运用各种相关知识及数形结合、分类讨论、转化等数学思想加以解决.当一个问题是确定有关图形的变量之间的关系时,通常建立函数模型或不等式模型求解;当确定图形之间的特殊位置关系或者一些特殊的值时,通常建立方程模型去求解.
2.存在性问题:二次函数常常与三角形、四边形和圆综合在一起运用,解决这类问题需要用到数形结合的数学思想,把“数”与“形”结合起来,互相渗透.存在探索型问题是指在给定条件下,判断某种数学现象是否存在、某个结论是否出现的问题.解决这类问题的一般思路是先假设结论的某一方面存在,然后在这个假设下进行演绎推理,若推出矛盾,则可否定假设;若推出合理结论,则可肯定假设.
课题 第3课时 二次函数与拱桥类问题 授课人
教 学 目 标 1.能根据具体的问题情境建立数学模型,应用二次函数的知识求解,并根据具体问题的实际意义检验结果的合理性. 2.学会从多个角度思考问题,逐步提高解决问题的能力. 3.通过对实际问题的研究,体会建模的数学思想. 4.经历将实际问题抽象为数学问题的过程,体会转化和数形结合的思想. 5.通过问题的设计、解答,使学生学会从不同角度寻求解决问题的方法,获得解决问题的经验. 6.通过小组合作交流,提高合作意识,培养创新精神. 7.通过用二次函数的知识解决实际问题,体会数学与现实生活的紧密联系,提高学习数学的兴趣,增强应用数学的意识.
教学 重点 探究应用二次函数的知识解决实际问题的方法.
教学 难点 如何从实际问题中抽象出数学问题,建立数学模型.
授课 类型 新授课 课时
教具 多媒体
教学活动
教学 步骤 师生活动 设计意图
回顾 1.二次函数解析式常见的形式有哪几种 说明其特征. 2.对二次函数y=ax2+bx+c的图象进行平移时: 向上平移k(k>0)个单位长度得到的图象对应的函数解析式是什么 向下平移k(k>0)个单位长度得到的图象对应的函数解析式是什么 向左平移h(h>0)个单位长度得到的图象对应的函数解析式是什么 向右平移h(h>0)个单位长度得到的图象对应的函数解析式是什么 师生活动:教师引导学生回忆知识,学生进行解答,教师做好点评. 在已有知识的基础上提出新的问题,能为学生营造一个主动思考、探索的氛围,激发学生的学习兴趣.
活动 一: 创设 情境 导入 新课 【课堂引入】 问题:图22-3-22是抛物线形拱桥,当拱顶离水面2米时,水面宽4米.若水面下降1米,则水面宽度将增加多少米 图22-3-22 师生活动: 教师进行引导,提出问题: 对于本题你认为应该运用什么知识进行解答 根据问题中的图形为抛物线,由此可知本题应该运用二次函数的知识进行解答. 学生分组讨论,如何利用函数模型解决问题,教师帮助学生解决问题. 通过日常生活中的实际问题,激发学生的学习兴趣,培养学生的探究意识和解决实际问题的能力.
活动 二: 探究 与 应用 1.探究新知 活动一:针对[课堂引入]的问题,教师进行提示: ①要解答二次函数的问题,必须把抛物线放在平面直角坐标系中,所以必须建立适当的平面直角坐标系; ②求水面增加的宽度,实际上就是求水面与抛物线的交点的坐标; ③求出函数解析式,进而求点的坐标; ④求函数解析式应该用待定系数法. 师生活动:学生先独立进行解答,然后小组内交流讨论,教师适时点拨,指导学生写出解题过程. 解:以抛物线的顶点为原点,对称轴为y轴,建立平面直角坐标系,如图22-3-23.根据图象的特殊性,设抛物线的函数解析式为y=ax2,由抛物线经过点A(-2,-2),可得a=-,所以抛物线的函数解析式为y=-x2.把y=-3代入函数解析式,得x=±,所以CD-AB=(2-4)米,则水面宽度将增加(2-4)米. 图22-3-23 活动二:教师指导学生建立不同的平面直角坐标系进行解答. 学生独立完成解题过程,小组内交流比较:建立的平面直角坐标系是否相同,计算结果是否一致. 如解法:如图22-3-24,设AB所在直线为x轴,经过AB的中点O且与AB垂直的直线为y轴,则通过画图可知O为原点,抛物线以y轴为对称轴,且经过A,B两点,可求出OA和OB的长为AB长的一半,即为2米,抛物线的顶点坐标为(0,2),通过以上条件可设解析式为顶点式y=ax2+2.将点A的坐标(-2,0)代入解析式,得a=-,所以抛物线的函数解析式为y=-x2+2.把y=-1代入上式,得x=±,所以CD-AB=米,则水面宽度将增加(2-4)米. 图22-3-24 2.归纳总结 教师引导学生进行归纳总结: ①建立适当的平面直角坐标系;②根据题意找出题目中的点的坐标;③求出抛物线的函数解析式;④直接利用图象解决实际问题. 1.通过建立不同的平面直角坐标系得到不同的函数解析式,但结果是相同的,选择合适的平面直角坐标系可以使解答更简便,更明确易懂. 2.通过总结抛物线形实际问题的解题步骤,使学生明确问题的解答方法,思路清晰,明确解题方向.
【应用举例】 例1 自动喷灌设备的喷流情况如图22-3-25所示,设水管AB在高出地面3.5米的B处有一自动旋转的喷水头,水流是抛物线形,喷头B与水流最高点C连线与地面成45°角,水流最高点C比喷头B高2米,求水流落点D到点A的距离. 师生活动:学生按要求进行解答,教师做好指导、点拨. 图22-3-25 教师关注: (1)学生能否熟练地运用二次函数的有关知识解决实际问题; (2)学生是否具有探索精神. 激发学生的学习欲望和兴趣,让学生切实感受到数学就在身边.让学生学会将获得的知识经验进行类比迁移,并让学生体验数学建模思想,增强应用意识.
活动 二: 探究 与 应用 【拓展提升】 例2 如图22-3-26,一场篮球赛中,小明跳起投篮,已知球出手时离地面米,与篮筐中心的水平距离为7米,当球出手后水平距离为4米时达到最大高度4米.设篮球运动的轨迹为抛物线,篮筐中心距离地面3.05米.此球能否投中篮筐 师生活动:学生独立解答,再合作交流,然后展示成果.教师巡视,观察学生解决问题的过程与方法,并给予学习有困难的学生及时的引导和帮助. 图22-3-26 通过抛物线与常见生活情景相联系的题目的展示,拓宽学生视野,提高学生灵活运用知识的能力.
活动 三: 课堂 总结 反思 【达标测评】 1.如图22-3-27所示的是一学生推铅球时铅球行进高度y(m)与水平距离x(m)之间的函数图象,观察图象,则铅球推出的水平距离是 10 m. 图22-3-27 2.小明以二次函数y=2x2-4x+8的图象为灵感为“北京房山国际葡萄酒大赛”设计了一款杯子,如图22-3-28为杯子的设计稿,若AB=4,DE=3,则杯子的高CE为 (B) 图22-3-28 A.14 B.11 C.6 D.3 3.某工厂的大门是一个抛物线形水泥建筑物,大门的地面宽度为8 m,两侧距地面3 m高处各有一盏壁灯,两盏壁灯之间的水平距离为6 m,如图22-3-29所示,则厂门的高约为 6.9 m (水泥建筑物厚度不计,精确到0.1 m). 图22-3-29 4.城市花园广场喷泉的喷嘴安装在平地上,有一喷嘴喷出的水流呈抛物线形,喷出水流的高度y(m)与喷出水流距喷嘴的水平距离x(m)之间满足函数解析式y=-x2+2x. (1)求喷嘴喷出的水流的最大高度是多少; (2)求喷嘴喷出的水流的最远距离是多少. 学生进行当堂检测,完成后,教师进行批阅、点评、讲解. 针对本课时的主要问题,从多个角度、分层次进行检测,达到学有所成、了解课堂学习效果的目的.
1.课堂总结: (1)你在本节课中有哪些收获 有哪些进步 (2)学习本节课后,还存在哪些困惑 2.布置作业: 教材第52页习题22.3第3题. 小结环节的设置能够让学生养成自主归纳课堂重点的习惯,提高学生的学习能力.
活动 三: 课堂 总结 反思 【知识网络】 提纲挈领,重点突出.
【教学反思】 ①[授课流程反思] 在探究新知环节中,充分利用多媒体手段提高课堂效率,激发学生的学习兴趣,调动学生的学习积极性,有效解决了教学的重难点;在课堂训练环节中,教师给予学生充分的自由时间,让学生能够体会建立平面直角坐标系的作用,明确解答问题的步骤,树立建模思想. ②[讲授效果反思] 教师强调重点:(1)明确解决抛物线形问题的步骤;(2)设抛物线的函数解析式时,要根据函数图象选择恰当的形式. ③[师生互动反思] 在开放、多样的教学活动中,培养学生主动合作的意识及对数学的兴趣和爱好. ④[习题反思] 好题题号 错题题号 反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
