小升初必考专题特训:图形与几何-数学六年级下册人教版(含解析)
文档属性
| 名称 | 小升初必考专题特训:图形与几何-数学六年级下册人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 520.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-12 22:48:34 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
小升初必考专题特训:图形与几何-数学六年级下册人教版
一、选择题
1.一段长为1米,横截面直径为20厘米的木头横着浮在水面上,它正好一半露出水面,则这段木头与水接触面的面积是( )平方厘米。
A.354.4 B.43140 C.3454 D.6908
2.用一个长12.56cm,宽9.42cm的长方形纸片当作侧面围成一个尽可能大的圆柱(不考虑接头处),下面哪个圆可以配上这个圆柱当底面?( )
A. B. C. D.
3.把一团圆柱形橡皮泥揉成与它等底的圆锥形,高将( )。
A.增加3倍 B.扩大到原来的3倍 C.缩小到原来的 D.缩小到原来的
4.等底等高的圆柱和圆锥的体积之差是9.42cm3,圆柱的体积是( )cm3。
A.3.14 B.4.71 C.9.42 D.14.13
5.一个长方形的面积是12平方厘米,按4∶1的比放大后它的面积是( )平方厘米。
A.48 B.96 C.192 D.768
6.在比例尺是1∶1000的图纸上,一个正方形的面积为64平方厘米,那么它的实际面积是( )平方米。
A.64 B.640 C.6400 D.64000
7.如图,将一个底面半径为1cm、高为2cm的圆柱切成两部分,下面说法正确的是( )。
A.甲种切法增加的表面积大 B.乙种切法增加的表面积大
C.两种切法增加的表面积相等 D.无法判断
8.如图,将这个容器倒过来后,水面的高度是( )厘米。
A.20 B.15 C.10 D.25
二、填空题
9.如下图,长方形由12个小正方形拼成,其中阴影部分的面积占长方形的( )%。
10.已知圆环的面积是,小圆和大圆的周长比是,则小圆的面积是( ),大圆的面积是( )。
11.有2厘米和3厘米长的小棒若干根,要做一个底面是边长3厘米的正方形、高是4厘米的长方体框架,需要选( )根2厘米长的小棒和( )根3厘米长的小棒;给这个框架表面糊上牛皮纸,需要( )平方厘米的牛皮纸。(接头处忽略不计)
12.一个三角形三个内角的度数比是1∶2∶3,这是一个( )三角形,如果这个三角形的面积一定,三角形的底和高成( )比例。
13.一个圆柱和一个圆锥,底面积的比是,高之比是,那么这个圆柱和圆锥的体积之比是( )。
14.图中正方形的面积是acm2,则圆的面积是( )cm2。
三、判断题
15.一个立体图形从正面看到的是,这个立体图形最少由2个小立方块组成。( )
16.棱长6cm的正方体,它的表面积和体积相等。( )
17.正方形的周长是米,则它的面积是平方米。( )
18.圆柱体的侧面积一定,底面周长和高成反比例。( )
19.当所铺正方形地面面积一定时,每块方砖的边长和所需的方砖数量成正比例。( )
四、计算题
20.图形与操作。
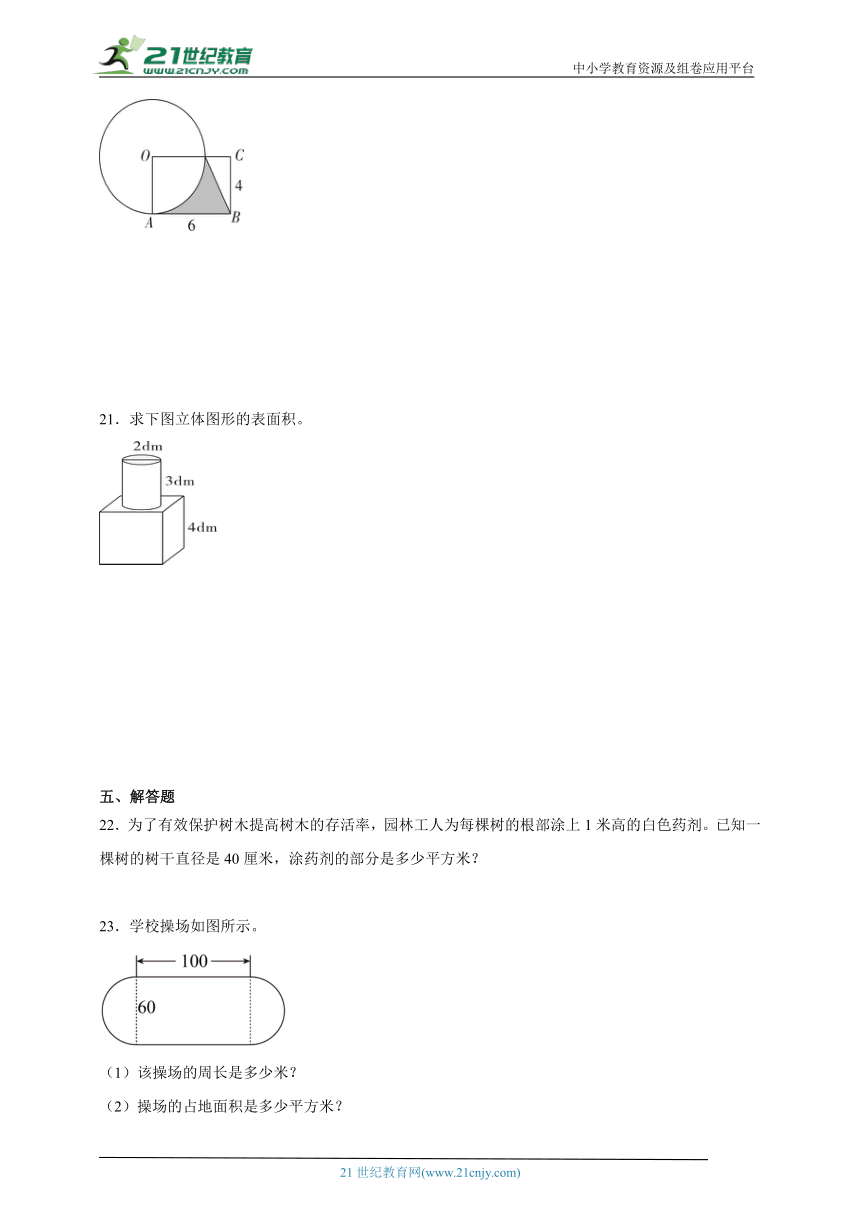
求下图阴影部分的面积。(单位:cm)
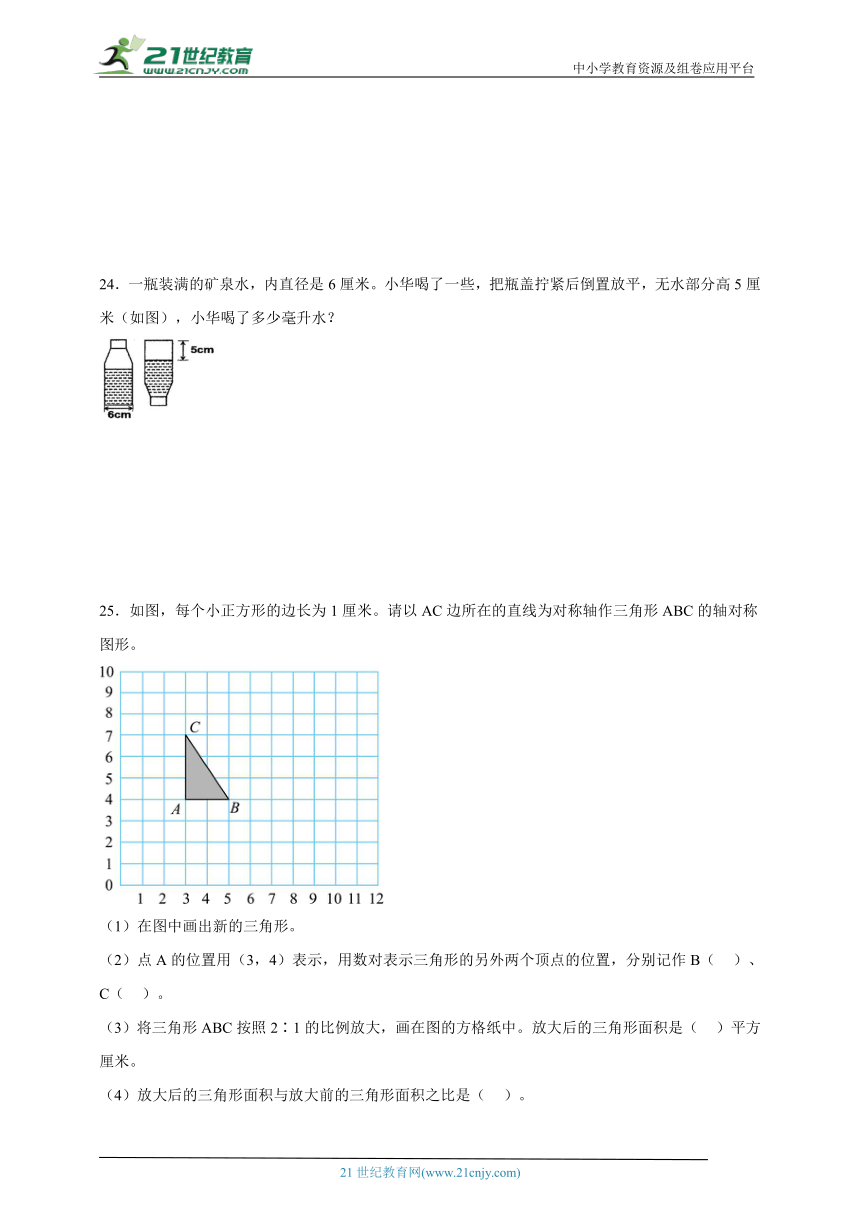
21.求下图立体图形的表面积。
五、解答题
22.为了有效保护树木提高树木的存活率,园林工人为每棵树的根部涂上1米高的白色药剂。已知一棵树的树干直径是40厘米,涂药剂的部分是多少平方米?
23.学校操场如图所示。
(1)该操场的周长是多少米?
(2)操场的占地面积是多少平方米?
24.一瓶装满的矿泉水,内直径是6厘米。小华喝了一些,把瓶盖拧紧后倒置放平,无水部分高5厘米(如图),小华喝了多少毫升水?
25.如图,每个小正方形的边长为1厘米。请以AC边所在的直线为对称轴作三角形ABC的轴对称图形。
(1)在图中画出新的三角形。
(2)点A的位置用(3,4)表示,用数对表示三角形的另外两个顶点的位置,分别记作B( )、C( )。
(3)将三角形ABC按照2∶1的比例放大,画在图的方格纸中。放大后的三角形面积是( )平方厘米。
(4)放大后的三角形面积与放大前的三角形面积之比是( )。
26.一个圆柱形易拉罐的高度正好等于一个圆锥形高脚杯的高度(如下图)。
(1)在易拉罐的侧面全部贴上商标纸,商标纸的面积是多少平方厘米?
(2)这个易拉罐在商标纸上标注“净含量:750毫升”,你认为商家做虚假宣传了吗?为什么?(饮料罐厚度忽略不计)
(3)把满罐饮料全部倒入高脚杯中,最多可以倒满几杯?(高脚杯的厚度忽略不计)
参考答案:
1.C
【分析】根据题意,这根木头与水接触的面的面积就是这根圆柱体木头表面积的一半,圆柱的表面积=,先将单位统一为厘米,再进行计算即可。
【详解】1米=100厘米
(平方厘米)
(平方厘米)
即这段木头与水接触面的面积是3454平方厘米;
故答案为:C
2.A
【分析】根据题意,长方形纸片的长或宽就是这个圆柱的底面周长。圆的周长=πd=2πr,据此分别以选项中的数为圆柱的底面直径或底面半径,求出相配的底面周长,看是否与长方形的长和宽相等,如果相等,则这个圆可以配上这个圆柱当底面,反之则不能。
【详解】A.3.14×4=12.56(cm),周长等于长方形纸片的长,则这个圆可以配上这个圆柱当底面;
B.3.14×6=18.84(cm),这个圆不可以配上这个圆柱当底面;
C.1.5×2×3.14=9.42(cm),这个圆不可以配上这个圆柱当底面;
D.4×2×3.14=25.12(cm),这个圆不可以配上这个圆柱当底面。
故答案为:A
3.B
【分析】根据题意可知,圆柱形橡皮泥的体积等于圆锥形橡皮泥的体积;根据圆柱的体积公式:体积=底面积×高;圆锥的体积公式:体积=底面积×高×;体积相等,底面积相等。这圆柱的高=圆锥的高×;圆锥的高=圆柱的高×3,即高将扩大到原来的3倍,据此解答。
【详解】根据分析可知,把一团圆柱形橡皮泥揉成与它等底的圆锥形,高将扩大到原来的3倍。
故答案为:B
4.D
【分析】因为等底等高的圆柱体积是圆锥体积的3倍,那么圆柱的体积就可以看作3份,圆锥的体积看作1份,它们相差2份。从题意可知,圆柱圆锥体积相差9.42 cm3,这9.42 cm3就对应两份的数量,用9.42÷2求出1份是多少,这1份就是圆锥的体积,接着再求3份是多少,即求出圆柱的体积。据此解答。
【详解】9.42÷(3-1)×3
=9.42÷2×3
=4.71×3
=14.13(cm3)
圆柱的体积是14.13 cm3。
故答案为:D
5.C
【分析】把图形按照n∶1放大,就是将图形的每一条边放大到原来的n倍,放大后图形与原图形对应边长的比是n∶1,因为长方形面积=长×宽,因此把长方形按照n∶1放大,面积扩大到原来的n×n倍,据此分析。
【详解】4×4=16
12×16=192(平方厘米)
按4∶1的比放大后它的面积是192平方厘米。
故答案为:C
6.C
【分析】一个正方形的面积为64平方厘米,64=8×8,所以图上距离正方形的边长是8厘米,根据实际距离=图上距离÷比例尺,代入数据求出正方形的实际距离,再根据正方形的面积=边长×边长即可解答。
【详解】64=8×8
8÷
=8×1000
=8000(厘米)
8000厘米=80米
80×80=6400(平方米)
正方形的实际面积是6400平方米。
故答案为:C
7.B
【分析】甲种切法增加的表面积:半径×半径×π×2;乙种切法增加的表面积:直径×高×2。数值代入计算后再比较大小即可。
【详解】12×3.14×2=6.28(平方厘米)
1×2×2×2=8(平方厘米)
6.28<8
乙种切法增加的表面积大。
故答案为:B
8.C
【分析】等体积等底面积的圆柱和圆锥,圆锥的高是圆柱高的3倍,因此将圆锥部分的高÷3,是倒过来水进入圆柱部分后的高,再加上原来圆柱部分水的高度即可。
【详解】15÷3+(20-15)
=5+5
=10(厘米)
水面的高度是10厘米。
故答案为:C
9.33/33.3/33.33
【分析】把小方格的边长看作单位“1”,这样长方形长就是6,宽是2,根据长方形的面积=长×宽即可求出长方形的面积。因此,阴影部分面积=长方形面积-三个空白三角形面积;三个空白三角形直角边已知,根据三角形面积S=ah÷2可求;求阴影部分面积是长方形面积的百分之几,用阴影部分面积除以长方形面积即可;
【详解】长方形的面积:6×2=12
三角形面积:2×1÷2=1
6×1÷2=3
4×2÷2
=8÷2
=4
12-(1+3+4)
=12-8
=4
4÷12×100%
≈0.333×100%
=33.3%
其中阴影部分的面积占长方形的33.3%。
10. 12.56 28.26
【分析】根据圆的周长公式C=2πr可知,两个圆的周长比等于它们的半径比。根据圆的面积公式S=πr2可知,两个圆的面积比等于它们半径的平方比。从“小圆和大圆的周长比是2∶3”可知,小圆和大圆的面积比是4∶9。因为圆环的面积=大圆的面积-小圆的面积,用圆环的面积÷(9-4),求出1份是多少,再求出4份,即小圆的面积,求出9份,即大圆的面积。据此解答。
【详解】22∶32=4∶9
15.7÷(9-4)
=15.7÷5
=3.14(dm2)
小圆的面积:3.14×4=12.56(dm2)
大圆的面积:3.14×9=28.26(dm2)
已知圆环的面积是,小圆和大圆的周长比是,则小圆的面积是(12.56),大圆的面积是(28.26)。
【点睛】明确两个圆的周长比等于它们的半径比,两个圆的面积比等于它们半径的平方比,是解题的关键。
11. 8 8 66
【分析】长方体有12条棱,其中有4条长,4条宽,4条高。从“底面是边长3厘米的正方形”可知,长和宽相等,那么需要8根3厘米的小棒;从“高是4厘米”可知,一条高要两根长2厘米的小棒,那么4条高就需要8根长2厘米的小棒。从“框架表面糊上牛皮纸”可知,牛皮纸的大小就是长方体的表面积。因为底面是正方形,那么上下面都是正方形,4×4即一个正方形的面积;长和宽相等,则前、后、左、右四个面是完全一样的长方形,3×4即一个长方形的面积。根据长方体的表面积是6个面的面积之和,列式计算即可求出牛皮纸的面积。据此解答。
【详解】高需要2厘米的小棒:4÷2×4=8(根)
长和宽共需要3厘米的小棒:4×2=8(根)
3×3×2+3×4×4
=18+48
=66(平方厘米)
因此需要8根2厘米长的小棒和8根3厘米长的小棒;给这个框架表面糊上牛皮纸,需要66平方厘米的牛皮纸。
12. 直角 反
【分析】用三角形内角和除以总份数即可求出每份是多少度,再乘3即可求出最大角的度数,由此判断是什么三角形;判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答。
【详解】180÷(1+2+3)×3
=180÷6×3
=30×3
=90(度)
最大的角是一个直角,所以这是一个直角三角形。
三角形面积=底×高÷2;则底×高=三角形面积×2(一定),底和高成反比例。
13.5∶4
【分析】根据题意,假设圆柱的底面积为2S,圆锥的底面积为3S,圆柱的高为5h,圆锥的高为8h,根据圆柱的体积=底面积×高,圆锥的体积=底面积×高÷3,求出二者的体积,再根据比的意义求出二者之比并化简。
【详解】假设圆柱的底面积为2S,圆锥的底面积为3S,圆柱的高为5h,圆锥的高为8h。
(2S×5h)∶(3S×8h÷3)
=10Sh∶8Sh
=(10Sh÷2Sh)∶(8Sh÷2Sh)
=5∶4
所以,这个圆柱和圆锥的体积之比是5∶4。
14.πa
【分析】根据正方形的面积=边长×边长,其中正方形的边长等于圆的半径,利用圆的面积=πr2,代入相应数值计算即可解答。
【详解】设圆的半径为r,圆的半径=正方形的边长
因为正方形的面积是a,即r×r=a(cm2)
所以圆的面积=πr2=πa(cm2)。
因此圆的面积是πa(cm2)。
15.√
【分析】根据从正面看到的形状,可知这个立体图形有2层,每层最少1个小立方块,据此分析。
【详解】
一个立体图形从正面看到的是,如图,这个立体图形最少由2个小立方块组成,说法正确。
故答案为:√
16.×
【分析】正方体表面积=棱长×棱长×6,正方体体积=棱长×棱长×棱长,物体表面面积的总和,叫做物体的表面积;体积是指物体所占空间的大小,表面积和体积是两种不同的量,无法进行比较,据此分析。
【详解】6×6×6=216(cm2)
6×6×6=216(cm3)
棱长6cm的正方体,它的表面积和体积的数值虽然相等,但是表面积和体积无法进行比较,所以原题说法错误。
故答案为:×
17.√
【分析】正方形的边长×4=周长,正方形的边长=周长÷4,据此求出正方形的边长,再根据正方形的面积=边长×边长解答。
【详解】
=
=(米)
(平方米)
所以正方形的面积是平方米。
所以原题说法正确。
故答案为:√
18.√
【分析】判断两种相关联的量是否成反比例,就看这两种量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果比值一定,就成正比例。
【详解】圆柱的底面周长×高=侧面积(一定),是乘积一定。
所以圆柱体的侧面积一定,底面周长和高成反比例。
故答案为:√
19.×
【分析】正比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的比值(或商)一定,那么它们的关系称为正比例关系。
反比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的积一定,那么它们的关系称为反比例关系。
由正反比例的定义可知,想要判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。本题中主要看每块方砖的边长和所需的方砖数量是比值一定还是乘积一定。由此可解答。
【详解】因为所需的方砖数量×每块方砖的面积=所铺地面的面积(一定),所以所需的方砖数量和每块方砖的面积成反比例。即所需的方砖数量和每块方砖边长的平方成反比例,但是所需的方砖数量与方砖的边长不成比例。
故答案为:×
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
20.7.44cm2
【分析】看图可知,阴影部分的面积=梯形面积-扇形面积,梯形上底和高都等于圆的半径,梯形面积=(上底+下底)×高÷2,扇形面积=圆周率×半径的平方÷4,据此列式计算。
【详解】(4+6)×4÷2-3.14×42÷4
=10×4÷2-3.14×16÷4
=20-12.56
=7.44(cm2)
阴影部分的面积是7.44cm2。
21.114.84dm2
【分析】由图可知,圆柱的上底面刚好填补正方体的上底面被覆盖的部分面积,因此图中立体图形的表面积可以看作是一个正方体的表面积加上一个圆柱的侧面积;根据正方体的表面积=棱长×棱长×6,圆柱的侧面积=底面周长×高,代入相应数值计算即可解答。
【详解】4×4×6+3.14×2×3
=16×6+6.28×3
=96+18.84
=114.84(dm2)
因此这个立体图形的表面积是114.84dm2。
22.1.256平方米
【分析】根据圆柱的侧面积=底面周长×高,把数据代入公式解答。
【详解】40厘米=0.4米
3.14×0.4×1
=1.256×1
=1.256(平方米)
答:涂药剂的部分是1.256平方米。
23.(1)388.4米
(2)8826平方米
【分析】(1)操场周长=圆的周长+长方形的长×2,圆的周长=圆周率×直径,据此列式解答;
(2)操场的占地面积=圆的面积+长方形面积,圆的面积=圆周率×半径的平方,长方形面积=长×宽,据此列式解答。
【详解】(1)3.14×60+100×2
=188.4+200
=388.4(米)
答:该操场的周长是388.4米。
(2)3.14×(60÷2)2+100×60
=3.14×302+6000
=3.14×900+6000
=2826+6000
=8826(平方米)
答:操场的占地面积是8826平方米。
24.141.3毫升
【分析】小华喝掉的水就是倒置后无水部分的体积,根据圆柱的体积等于底面积×高,设一个圆柱底面半径为r,高为h,则体积V=πr2h;如S为底面积,高为h,体积为V:则V=Sh,也即V=πr2h。据此求出h即可。
【详解】3.14×(6÷2)2×5
=3.14×32×5
=3.14×9×5
=28.26×5
=141.3(立方厘米)
141.3立方厘米=141.3毫升
答:小华喝了141.3毫升水。
25.(1)(3)图见详解
(2)(5,4);(3,7);
(3)12
(4)4∶1
【分析】(1)根据轴对称图形的意义:对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出原半图的关键对称点,依次连接即可。
(2)根据数对表示位置的方法:第一个数表示列,第二个数表示行,据此解答;
(3)将三角形的底边和高分别扩大2倍求出扩大后的底边与高,根据三角形面积公式:面积=底×高÷2,计算出面积,画出扩大后的三角形即可;
(4)根据三角形面积公式,计算出放大前三角形的面积,再根据比的意义:用放大后三角形的面积∶放大前三角形面积,化简,即可解答。
【详解】(1)如下图:
(2)B(5,4),C(3,7)
点A的位置用(3,4)表示,用数对表示三角形的另外两个顶点的位置,分别记作B(5,4),C(3,7)。
(3)图如下:
放大后三角形的底是:2×2=4(厘米),高是:2×3=6(厘米);
面积:4×6÷2
=24÷2
=12(平方厘米)
放大后的三角形面积是12平方厘米。
(4)12∶(2×3÷2)
=12∶(6÷2)
=12∶3
=(12÷3)∶(3÷3)
=4∶1
放大后的三角形面积与放大前的三角形面积之比是4∶1。
26.(1)376.8平方厘米;
(2)没有;容积大于750毫升
(3)4杯
【分析】(1)根据圆柱侧面积=底面周长×高,列式解答即可;
(2)根据圆柱体积=底面积×高,求出易拉罐的容积,与标注的净含量比较即可;
(3)根据圆锥体积=底面积×高÷3,求出高脚杯的容积,易拉罐容积÷高脚杯容积,结果用去尾法保留近似数即可。
【详解】(1)9+6=15(厘米)
3.14×8×15=376.8(平方厘米)
答:商标纸的面积是376.8平方厘米。
(2)8÷2=4(厘米)
3.14×42×15
=3.14×16×15
=753.6(立方厘米)
=753.6(毫升)
753.6毫升>750毫升
答:商家没有做虚假宣传,因为罐内容积大于750毫升。
(3)10÷2=5(厘米)
3.14×52×6÷3
=3.14×25×6÷3
=157(立方厘米)
=157(毫升)
753.6÷157≈4(杯)
答:最多可以倒满4杯。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
小升初必考专题特训:图形与几何-数学六年级下册人教版
一、选择题
1.一段长为1米,横截面直径为20厘米的木头横着浮在水面上,它正好一半露出水面,则这段木头与水接触面的面积是( )平方厘米。
A.354.4 B.43140 C.3454 D.6908
2.用一个长12.56cm,宽9.42cm的长方形纸片当作侧面围成一个尽可能大的圆柱(不考虑接头处),下面哪个圆可以配上这个圆柱当底面?( )
A. B. C. D.
3.把一团圆柱形橡皮泥揉成与它等底的圆锥形,高将( )。
A.增加3倍 B.扩大到原来的3倍 C.缩小到原来的 D.缩小到原来的
4.等底等高的圆柱和圆锥的体积之差是9.42cm3,圆柱的体积是( )cm3。
A.3.14 B.4.71 C.9.42 D.14.13
5.一个长方形的面积是12平方厘米,按4∶1的比放大后它的面积是( )平方厘米。
A.48 B.96 C.192 D.768
6.在比例尺是1∶1000的图纸上,一个正方形的面积为64平方厘米,那么它的实际面积是( )平方米。
A.64 B.640 C.6400 D.64000
7.如图,将一个底面半径为1cm、高为2cm的圆柱切成两部分,下面说法正确的是( )。
A.甲种切法增加的表面积大 B.乙种切法增加的表面积大
C.两种切法增加的表面积相等 D.无法判断
8.如图,将这个容器倒过来后,水面的高度是( )厘米。
A.20 B.15 C.10 D.25
二、填空题
9.如下图,长方形由12个小正方形拼成,其中阴影部分的面积占长方形的( )%。
10.已知圆环的面积是,小圆和大圆的周长比是,则小圆的面积是( ),大圆的面积是( )。
11.有2厘米和3厘米长的小棒若干根,要做一个底面是边长3厘米的正方形、高是4厘米的长方体框架,需要选( )根2厘米长的小棒和( )根3厘米长的小棒;给这个框架表面糊上牛皮纸,需要( )平方厘米的牛皮纸。(接头处忽略不计)
12.一个三角形三个内角的度数比是1∶2∶3,这是一个( )三角形,如果这个三角形的面积一定,三角形的底和高成( )比例。
13.一个圆柱和一个圆锥,底面积的比是,高之比是,那么这个圆柱和圆锥的体积之比是( )。
14.图中正方形的面积是acm2,则圆的面积是( )cm2。
三、判断题
15.一个立体图形从正面看到的是,这个立体图形最少由2个小立方块组成。( )
16.棱长6cm的正方体,它的表面积和体积相等。( )
17.正方形的周长是米,则它的面积是平方米。( )
18.圆柱体的侧面积一定,底面周长和高成反比例。( )
19.当所铺正方形地面面积一定时,每块方砖的边长和所需的方砖数量成正比例。( )
四、计算题
20.图形与操作。
求下图阴影部分的面积。(单位:cm)
21.求下图立体图形的表面积。
五、解答题
22.为了有效保护树木提高树木的存活率,园林工人为每棵树的根部涂上1米高的白色药剂。已知一棵树的树干直径是40厘米,涂药剂的部分是多少平方米?
23.学校操场如图所示。
(1)该操场的周长是多少米?
(2)操场的占地面积是多少平方米?
24.一瓶装满的矿泉水,内直径是6厘米。小华喝了一些,把瓶盖拧紧后倒置放平,无水部分高5厘米(如图),小华喝了多少毫升水?
25.如图,每个小正方形的边长为1厘米。请以AC边所在的直线为对称轴作三角形ABC的轴对称图形。
(1)在图中画出新的三角形。
(2)点A的位置用(3,4)表示,用数对表示三角形的另外两个顶点的位置,分别记作B( )、C( )。
(3)将三角形ABC按照2∶1的比例放大,画在图的方格纸中。放大后的三角形面积是( )平方厘米。
(4)放大后的三角形面积与放大前的三角形面积之比是( )。
26.一个圆柱形易拉罐的高度正好等于一个圆锥形高脚杯的高度(如下图)。
(1)在易拉罐的侧面全部贴上商标纸,商标纸的面积是多少平方厘米?
(2)这个易拉罐在商标纸上标注“净含量:750毫升”,你认为商家做虚假宣传了吗?为什么?(饮料罐厚度忽略不计)
(3)把满罐饮料全部倒入高脚杯中,最多可以倒满几杯?(高脚杯的厚度忽略不计)
参考答案:
1.C
【分析】根据题意,这根木头与水接触的面的面积就是这根圆柱体木头表面积的一半,圆柱的表面积=,先将单位统一为厘米,再进行计算即可。
【详解】1米=100厘米
(平方厘米)
(平方厘米)
即这段木头与水接触面的面积是3454平方厘米;
故答案为:C
2.A
【分析】根据题意,长方形纸片的长或宽就是这个圆柱的底面周长。圆的周长=πd=2πr,据此分别以选项中的数为圆柱的底面直径或底面半径,求出相配的底面周长,看是否与长方形的长和宽相等,如果相等,则这个圆可以配上这个圆柱当底面,反之则不能。
【详解】A.3.14×4=12.56(cm),周长等于长方形纸片的长,则这个圆可以配上这个圆柱当底面;
B.3.14×6=18.84(cm),这个圆不可以配上这个圆柱当底面;
C.1.5×2×3.14=9.42(cm),这个圆不可以配上这个圆柱当底面;
D.4×2×3.14=25.12(cm),这个圆不可以配上这个圆柱当底面。
故答案为:A
3.B
【分析】根据题意可知,圆柱形橡皮泥的体积等于圆锥形橡皮泥的体积;根据圆柱的体积公式:体积=底面积×高;圆锥的体积公式:体积=底面积×高×;体积相等,底面积相等。这圆柱的高=圆锥的高×;圆锥的高=圆柱的高×3,即高将扩大到原来的3倍,据此解答。
【详解】根据分析可知,把一团圆柱形橡皮泥揉成与它等底的圆锥形,高将扩大到原来的3倍。
故答案为:B
4.D
【分析】因为等底等高的圆柱体积是圆锥体积的3倍,那么圆柱的体积就可以看作3份,圆锥的体积看作1份,它们相差2份。从题意可知,圆柱圆锥体积相差9.42 cm3,这9.42 cm3就对应两份的数量,用9.42÷2求出1份是多少,这1份就是圆锥的体积,接着再求3份是多少,即求出圆柱的体积。据此解答。
【详解】9.42÷(3-1)×3
=9.42÷2×3
=4.71×3
=14.13(cm3)
圆柱的体积是14.13 cm3。
故答案为:D
5.C
【分析】把图形按照n∶1放大,就是将图形的每一条边放大到原来的n倍,放大后图形与原图形对应边长的比是n∶1,因为长方形面积=长×宽,因此把长方形按照n∶1放大,面积扩大到原来的n×n倍,据此分析。
【详解】4×4=16
12×16=192(平方厘米)
按4∶1的比放大后它的面积是192平方厘米。
故答案为:C
6.C
【分析】一个正方形的面积为64平方厘米,64=8×8,所以图上距离正方形的边长是8厘米,根据实际距离=图上距离÷比例尺,代入数据求出正方形的实际距离,再根据正方形的面积=边长×边长即可解答。
【详解】64=8×8
8÷
=8×1000
=8000(厘米)
8000厘米=80米
80×80=6400(平方米)
正方形的实际面积是6400平方米。
故答案为:C
7.B
【分析】甲种切法增加的表面积:半径×半径×π×2;乙种切法增加的表面积:直径×高×2。数值代入计算后再比较大小即可。
【详解】12×3.14×2=6.28(平方厘米)
1×2×2×2=8(平方厘米)
6.28<8
乙种切法增加的表面积大。
故答案为:B
8.C
【分析】等体积等底面积的圆柱和圆锥,圆锥的高是圆柱高的3倍,因此将圆锥部分的高÷3,是倒过来水进入圆柱部分后的高,再加上原来圆柱部分水的高度即可。
【详解】15÷3+(20-15)
=5+5
=10(厘米)
水面的高度是10厘米。
故答案为:C
9.33/33.3/33.33
【分析】把小方格的边长看作单位“1”,这样长方形长就是6,宽是2,根据长方形的面积=长×宽即可求出长方形的面积。因此,阴影部分面积=长方形面积-三个空白三角形面积;三个空白三角形直角边已知,根据三角形面积S=ah÷2可求;求阴影部分面积是长方形面积的百分之几,用阴影部分面积除以长方形面积即可;
【详解】长方形的面积:6×2=12
三角形面积:2×1÷2=1
6×1÷2=3
4×2÷2
=8÷2
=4
12-(1+3+4)
=12-8
=4
4÷12×100%
≈0.333×100%
=33.3%
其中阴影部分的面积占长方形的33.3%。
10. 12.56 28.26
【分析】根据圆的周长公式C=2πr可知,两个圆的周长比等于它们的半径比。根据圆的面积公式S=πr2可知,两个圆的面积比等于它们半径的平方比。从“小圆和大圆的周长比是2∶3”可知,小圆和大圆的面积比是4∶9。因为圆环的面积=大圆的面积-小圆的面积,用圆环的面积÷(9-4),求出1份是多少,再求出4份,即小圆的面积,求出9份,即大圆的面积。据此解答。
【详解】22∶32=4∶9
15.7÷(9-4)
=15.7÷5
=3.14(dm2)
小圆的面积:3.14×4=12.56(dm2)
大圆的面积:3.14×9=28.26(dm2)
已知圆环的面积是,小圆和大圆的周长比是,则小圆的面积是(12.56),大圆的面积是(28.26)。
【点睛】明确两个圆的周长比等于它们的半径比,两个圆的面积比等于它们半径的平方比,是解题的关键。
11. 8 8 66
【分析】长方体有12条棱,其中有4条长,4条宽,4条高。从“底面是边长3厘米的正方形”可知,长和宽相等,那么需要8根3厘米的小棒;从“高是4厘米”可知,一条高要两根长2厘米的小棒,那么4条高就需要8根长2厘米的小棒。从“框架表面糊上牛皮纸”可知,牛皮纸的大小就是长方体的表面积。因为底面是正方形,那么上下面都是正方形,4×4即一个正方形的面积;长和宽相等,则前、后、左、右四个面是完全一样的长方形,3×4即一个长方形的面积。根据长方体的表面积是6个面的面积之和,列式计算即可求出牛皮纸的面积。据此解答。
【详解】高需要2厘米的小棒:4÷2×4=8(根)
长和宽共需要3厘米的小棒:4×2=8(根)
3×3×2+3×4×4
=18+48
=66(平方厘米)
因此需要8根2厘米长的小棒和8根3厘米长的小棒;给这个框架表面糊上牛皮纸,需要66平方厘米的牛皮纸。
12. 直角 反
【分析】用三角形内角和除以总份数即可求出每份是多少度,再乘3即可求出最大角的度数,由此判断是什么三角形;判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答。
【详解】180÷(1+2+3)×3
=180÷6×3
=30×3
=90(度)
最大的角是一个直角,所以这是一个直角三角形。
三角形面积=底×高÷2;则底×高=三角形面积×2(一定),底和高成反比例。
13.5∶4
【分析】根据题意,假设圆柱的底面积为2S,圆锥的底面积为3S,圆柱的高为5h,圆锥的高为8h,根据圆柱的体积=底面积×高,圆锥的体积=底面积×高÷3,求出二者的体积,再根据比的意义求出二者之比并化简。
【详解】假设圆柱的底面积为2S,圆锥的底面积为3S,圆柱的高为5h,圆锥的高为8h。
(2S×5h)∶(3S×8h÷3)
=10Sh∶8Sh
=(10Sh÷2Sh)∶(8Sh÷2Sh)
=5∶4
所以,这个圆柱和圆锥的体积之比是5∶4。
14.πa
【分析】根据正方形的面积=边长×边长,其中正方形的边长等于圆的半径,利用圆的面积=πr2,代入相应数值计算即可解答。
【详解】设圆的半径为r,圆的半径=正方形的边长
因为正方形的面积是a,即r×r=a(cm2)
所以圆的面积=πr2=πa(cm2)。
因此圆的面积是πa(cm2)。
15.√
【分析】根据从正面看到的形状,可知这个立体图形有2层,每层最少1个小立方块,据此分析。
【详解】
一个立体图形从正面看到的是,如图,这个立体图形最少由2个小立方块组成,说法正确。
故答案为:√
16.×
【分析】正方体表面积=棱长×棱长×6,正方体体积=棱长×棱长×棱长,物体表面面积的总和,叫做物体的表面积;体积是指物体所占空间的大小,表面积和体积是两种不同的量,无法进行比较,据此分析。
【详解】6×6×6=216(cm2)
6×6×6=216(cm3)
棱长6cm的正方体,它的表面积和体积的数值虽然相等,但是表面积和体积无法进行比较,所以原题说法错误。
故答案为:×
17.√
【分析】正方形的边长×4=周长,正方形的边长=周长÷4,据此求出正方形的边长,再根据正方形的面积=边长×边长解答。
【详解】
=
=(米)
(平方米)
所以正方形的面积是平方米。
所以原题说法正确。
故答案为:√
18.√
【分析】判断两种相关联的量是否成反比例,就看这两种量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果比值一定,就成正比例。
【详解】圆柱的底面周长×高=侧面积(一定),是乘积一定。
所以圆柱体的侧面积一定,底面周长和高成反比例。
故答案为:√
19.×
【分析】正比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的比值(或商)一定,那么它们的关系称为正比例关系。
反比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的积一定,那么它们的关系称为反比例关系。
由正反比例的定义可知,想要判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。本题中主要看每块方砖的边长和所需的方砖数量是比值一定还是乘积一定。由此可解答。
【详解】因为所需的方砖数量×每块方砖的面积=所铺地面的面积(一定),所以所需的方砖数量和每块方砖的面积成反比例。即所需的方砖数量和每块方砖边长的平方成反比例,但是所需的方砖数量与方砖的边长不成比例。
故答案为:×
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
20.7.44cm2
【分析】看图可知,阴影部分的面积=梯形面积-扇形面积,梯形上底和高都等于圆的半径,梯形面积=(上底+下底)×高÷2,扇形面积=圆周率×半径的平方÷4,据此列式计算。
【详解】(4+6)×4÷2-3.14×42÷4
=10×4÷2-3.14×16÷4
=20-12.56
=7.44(cm2)
阴影部分的面积是7.44cm2。
21.114.84dm2
【分析】由图可知,圆柱的上底面刚好填补正方体的上底面被覆盖的部分面积,因此图中立体图形的表面积可以看作是一个正方体的表面积加上一个圆柱的侧面积;根据正方体的表面积=棱长×棱长×6,圆柱的侧面积=底面周长×高,代入相应数值计算即可解答。
【详解】4×4×6+3.14×2×3
=16×6+6.28×3
=96+18.84
=114.84(dm2)
因此这个立体图形的表面积是114.84dm2。
22.1.256平方米
【分析】根据圆柱的侧面积=底面周长×高,把数据代入公式解答。
【详解】40厘米=0.4米
3.14×0.4×1
=1.256×1
=1.256(平方米)
答:涂药剂的部分是1.256平方米。
23.(1)388.4米
(2)8826平方米
【分析】(1)操场周长=圆的周长+长方形的长×2,圆的周长=圆周率×直径,据此列式解答;
(2)操场的占地面积=圆的面积+长方形面积,圆的面积=圆周率×半径的平方,长方形面积=长×宽,据此列式解答。
【详解】(1)3.14×60+100×2
=188.4+200
=388.4(米)
答:该操场的周长是388.4米。
(2)3.14×(60÷2)2+100×60
=3.14×302+6000
=3.14×900+6000
=2826+6000
=8826(平方米)
答:操场的占地面积是8826平方米。
24.141.3毫升
【分析】小华喝掉的水就是倒置后无水部分的体积,根据圆柱的体积等于底面积×高,设一个圆柱底面半径为r,高为h,则体积V=πr2h;如S为底面积,高为h,体积为V:则V=Sh,也即V=πr2h。据此求出h即可。
【详解】3.14×(6÷2)2×5
=3.14×32×5
=3.14×9×5
=28.26×5
=141.3(立方厘米)
141.3立方厘米=141.3毫升
答:小华喝了141.3毫升水。
25.(1)(3)图见详解
(2)(5,4);(3,7);
(3)12
(4)4∶1
【分析】(1)根据轴对称图形的意义:对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出原半图的关键对称点,依次连接即可。
(2)根据数对表示位置的方法:第一个数表示列,第二个数表示行,据此解答;
(3)将三角形的底边和高分别扩大2倍求出扩大后的底边与高,根据三角形面积公式:面积=底×高÷2,计算出面积,画出扩大后的三角形即可;
(4)根据三角形面积公式,计算出放大前三角形的面积,再根据比的意义:用放大后三角形的面积∶放大前三角形面积,化简,即可解答。
【详解】(1)如下图:
(2)B(5,4),C(3,7)
点A的位置用(3,4)表示,用数对表示三角形的另外两个顶点的位置,分别记作B(5,4),C(3,7)。
(3)图如下:
放大后三角形的底是:2×2=4(厘米),高是:2×3=6(厘米);
面积:4×6÷2
=24÷2
=12(平方厘米)
放大后的三角形面积是12平方厘米。
(4)12∶(2×3÷2)
=12∶(6÷2)
=12∶3
=(12÷3)∶(3÷3)
=4∶1
放大后的三角形面积与放大前的三角形面积之比是4∶1。
26.(1)376.8平方厘米;
(2)没有;容积大于750毫升
(3)4杯
【分析】(1)根据圆柱侧面积=底面周长×高,列式解答即可;
(2)根据圆柱体积=底面积×高,求出易拉罐的容积,与标注的净含量比较即可;
(3)根据圆锥体积=底面积×高÷3,求出高脚杯的容积,易拉罐容积÷高脚杯容积,结果用去尾法保留近似数即可。
【详解】(1)9+6=15(厘米)
3.14×8×15=376.8(平方厘米)
答:商标纸的面积是376.8平方厘米。
(2)8÷2=4(厘米)
3.14×42×15
=3.14×16×15
=753.6(立方厘米)
=753.6(毫升)
753.6毫升>750毫升
答:商家没有做虚假宣传,因为罐内容积大于750毫升。
(3)10÷2=5(厘米)
3.14×52×6÷3
=3.14×25×6÷3
=157(立方厘米)
=157(毫升)
753.6÷157≈4(杯)
答:最多可以倒满4杯。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
