实数与向量相乘
图片预览


文档简介
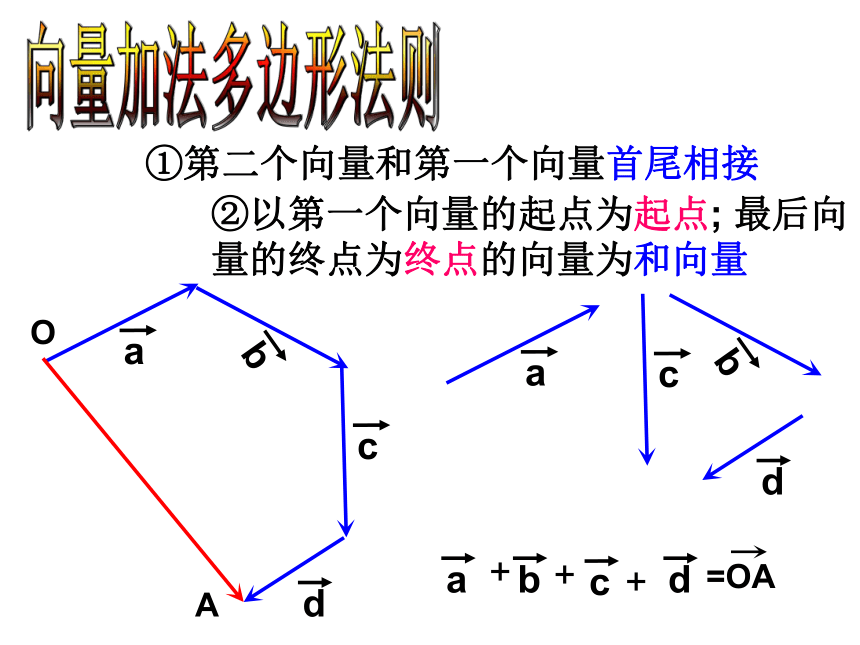
课件18张PPT。①第二个向量和第一个向量首尾相接②以第一个向量的起点为起点; 第二个向量的终点为终点的向量为和向量向量的加法的法则----三角形法则ABC向量加法多边形法则①第二个向量和第一个向量首尾相接②以第一个向量的起点为起点; 最后向量的终点为终点的向量为和向量+++OA①两个向量有公共起点.
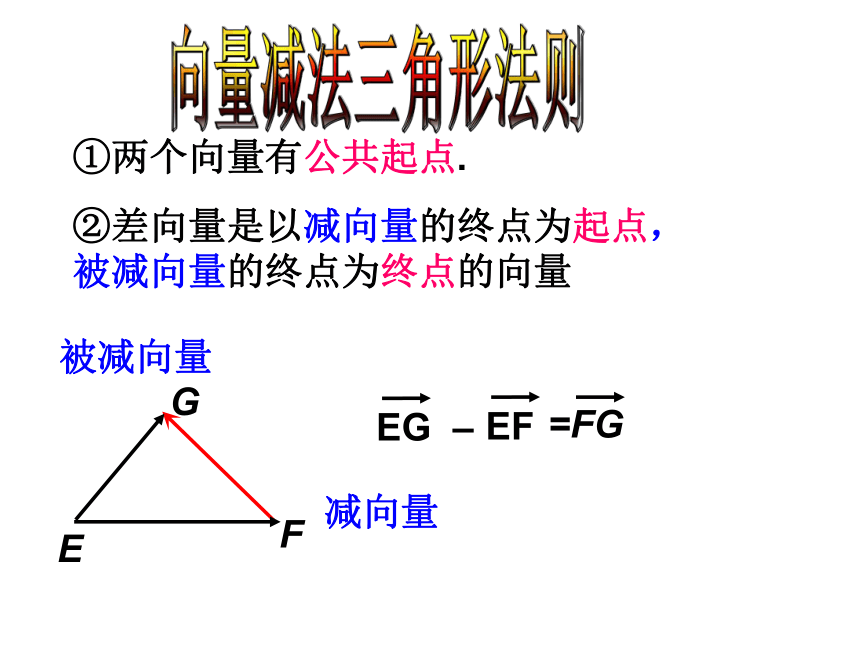
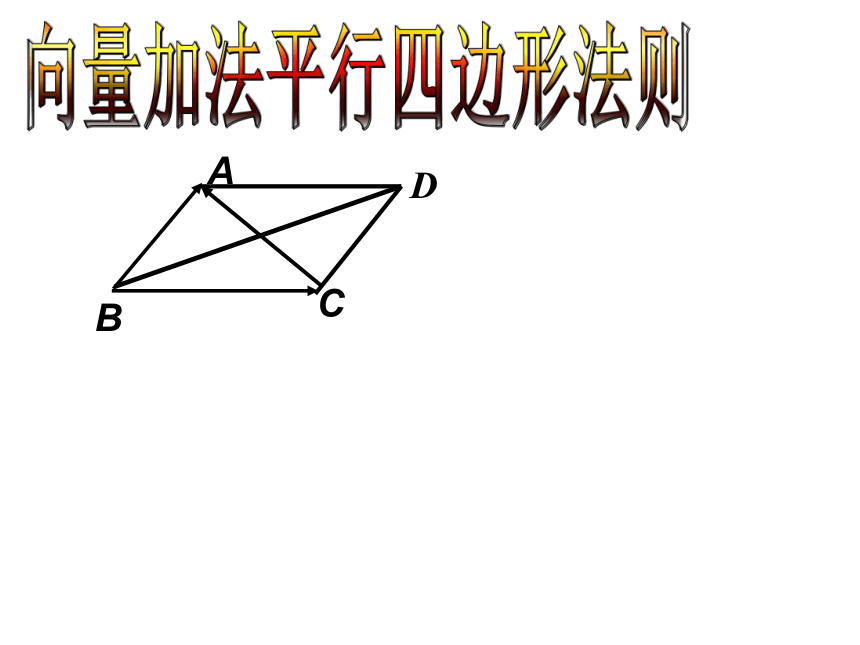
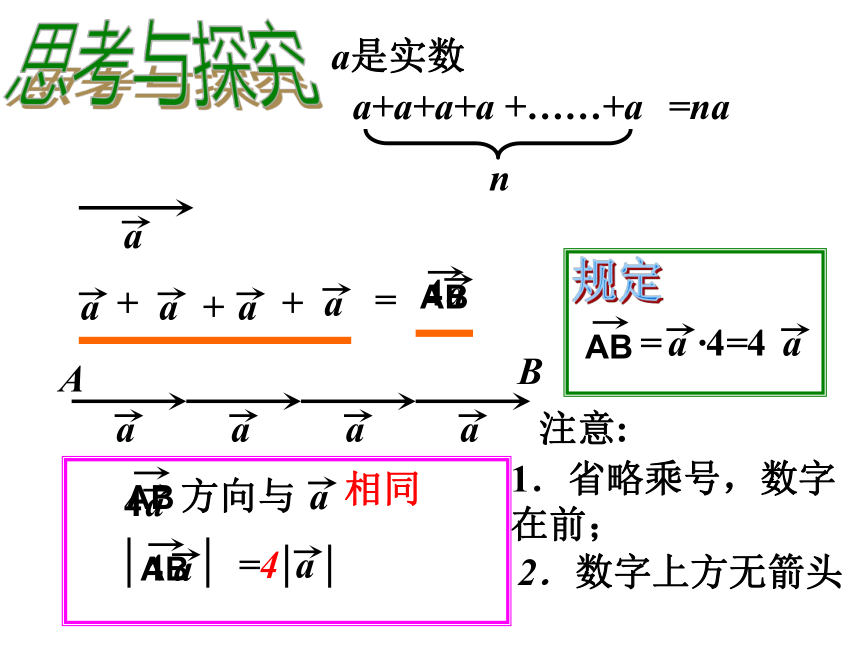
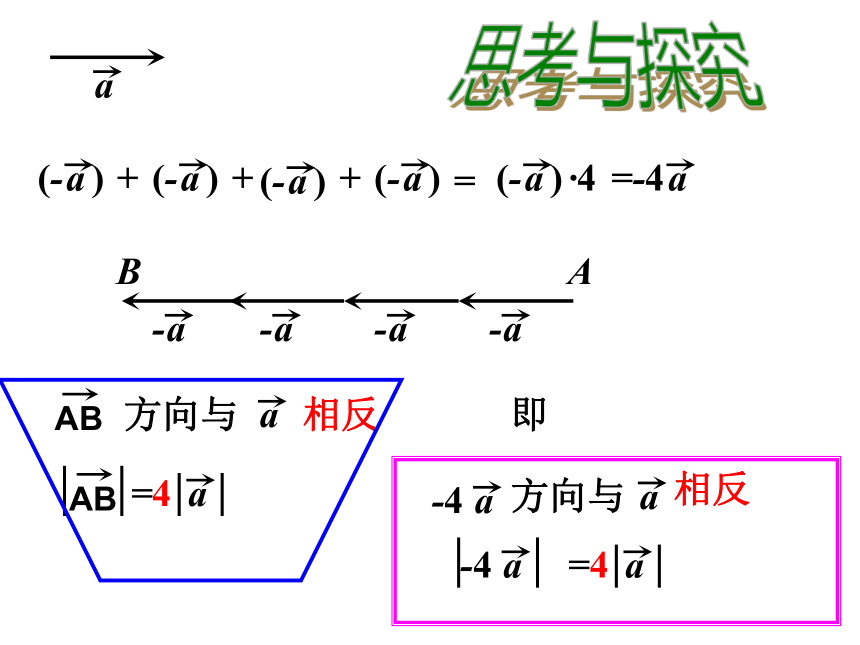
②差向量是以减向量的终点为起点,被减向量的终点为终点的向量向量减法三角形法则减向量被减向量向量加法平行四边形法则D§24.6实数与向量相乘(1)思考与探究 =naa是实数a+a+a+a +……+an+++=AB方向与相同=4规定·4=注意:1.省略乘号,数字在前;2.数字上方无箭头思考与探究 +++=AB方向与相反=4·4方向与相反=4即与的关系是什么?思考方向与相同方向与相反⑴若k≠0,且a ≠ 0,
则 的长度 =
方向为:k>0时, 与 同方向;
k<0时, 与 反方向;
⑵.若k=0 或 =0,则 = 0 .实数与向量相乘k是实数例1. 已知非零向量a,求作: a , b.
a
(1)(2)(3)例2.如图:在 ABCD中,E,F,G,H分别为各边的中点,EG与FH相交于点O,设AD=a,BA=b,试用向量a或b表示向量OE,OF,并写出图中与OE相等的向量.例3.如图:已知点D,E在ABC的边AB,AC上,DE∥BC,AD=4DB,试用向量BC表示向量DE.例4.如图:已知点D,E在ABC的边AB,AC上,DE∥BC, ,试用向量BC表示向量DE.5梯形ABCD,AB//CD,F、E在AD、BC,EF//CD,且3AB=2CD,CE=2BE,试用表示6.如图:设A,B为两定点,且PA=3AB (m为实数),O为直线外一点,若OA=a, OB=b,试用a,b表示OP.实数与向量相乘的意义及表示法;
若 K≠O,且a ≠O,则:Ka的长度为:
3. 的方向:1)当K>0时, 与a同方向;
2)当K<0时, 与a反方向;
3)若K=0或a=0,则: =0.
.课堂小结布置作业1.《练习部分》; 《一课一练》;
2.预习:§24.6(2);应用与思考 7. 在⊿ABC中,D,E,F分别为AB,BC,CA的中点,G为
重心,求证:GD+GE+GF=0. AFEDCBG
②差向量是以减向量的终点为起点,被减向量的终点为终点的向量向量减法三角形法则减向量被减向量向量加法平行四边形法则D§24.6实数与向量相乘(1)思考与探究 =naa是实数a+a+a+a +……+an+++=AB方向与相同=4规定·4=注意:1.省略乘号,数字在前;2.数字上方无箭头思考与探究 +++=AB方向与相反=4·4方向与相反=4即与的关系是什么?思考方向与相同方向与相反⑴若k≠0,且a ≠ 0,
则 的长度 =
方向为:k>0时, 与 同方向;
k<0时, 与 反方向;
⑵.若k=0 或 =0,则 = 0 .实数与向量相乘k是实数例1. 已知非零向量a,求作: a , b.
a
(1)(2)(3)例2.如图:在 ABCD中,E,F,G,H分别为各边的中点,EG与FH相交于点O,设AD=a,BA=b,试用向量a或b表示向量OE,OF,并写出图中与OE相等的向量.例3.如图:已知点D,E在ABC的边AB,AC上,DE∥BC,AD=4DB,试用向量BC表示向量DE.例4.如图:已知点D,E在ABC的边AB,AC上,DE∥BC, ,试用向量BC表示向量DE.5梯形ABCD,AB//CD,F、E在AD、BC,EF//CD,且3AB=2CD,CE=2BE,试用表示6.如图:设A,B为两定点,且PA=3AB (m为实数),O为直线外一点,若OA=a, OB=b,试用a,b表示OP.实数与向量相乘的意义及表示法;
若 K≠O,且a ≠O,则:Ka的长度为:
3. 的方向:1)当K>0时, 与a同方向;
2)当K<0时, 与a反方向;
3)若K=0或a=0,则: =0.
.课堂小结布置作业1.《练习部分》; 《一课一练》;
2.预习:§24.6(2);应用与思考 7. 在⊿ABC中,D,E,F分别为AB,BC,CA的中点,G为
重心,求证:GD+GE+GF=0. AFEDCBG
