第2章 整式及其加减 小结与复习 课件(共24张PPT)2024-2025学年沪科版七年级数学上册
文档属性
| 名称 | 第2章 整式及其加减 小结与复习 课件(共24张PPT)2024-2025学年沪科版七年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-12 18:50:06 | ||
图片预览








文档简介
(共24张PPT)
七年级上册数学(沪科版)
小结与复习
第 2 章 整式及其加减
e7d195523061f1c0c2b73831c94a3edc981f60e396d3e182073EE1468018468A7F192AE5E5CD515B6C3125F8AF6E4EE646174E8CF0B46FD19828DCE8CDA3B3A044A74F0E769C5FA8CB87AB6FC303C8BA3785FAC64AF5424764E128FECAE4CC72932BB65C8C121A0F41C1707D94688ED66335DC6AE12288BF2055523C0C26863D2CD4AC454A29EEC183CEF0375334B579
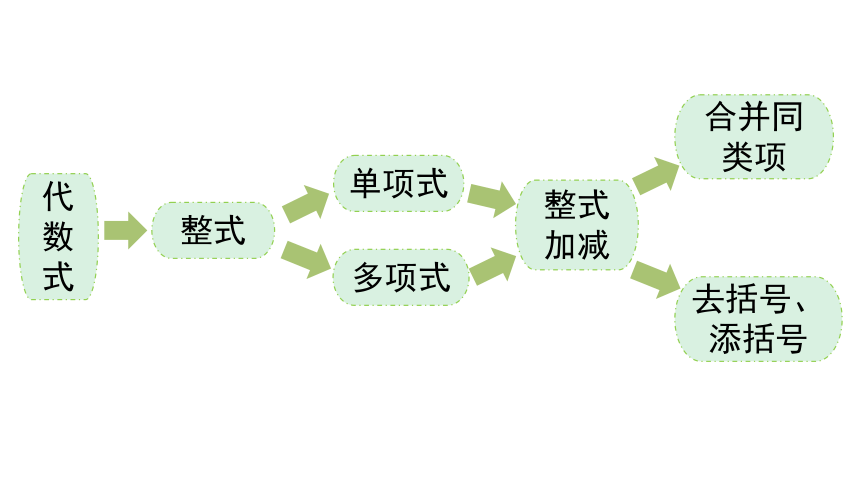
代数式
整式
单项式
多项式
整式加减
合并同类项
去括号、添括号
一、整式的有关概念
1. 代数式:用加、减、乘、除及乘方等运算符号将数或表示数的字母连接而成的式子,叫作代数式. 单个的数或字母也是代数式.
2. 单项式:都是数与字母的____,这样的式子叫作单项式,单个的字母或数也是单项式.
3. 单项式的系数:单项式中的数字因数叫作这个单项式的系数.
4. 单项式的次数:一个单项式中,所有字母的指数的和叫作这个单项式的次数.
积
5. 多项式:几个单项式的____叫作多项式.
6. 多项式的项:多项式中,每个单项式(连同符号)叫做多项式的项.其中不含字母的项叫做常数项.一个多项式有几项,这个多项式就叫做几项式.
7. 多项式的次数:多项式里次数最高的项的次数,叫做这个多项式的次数.
8. 整式:____________________统称整式.
9. 代数式的值:用数字替代代数式里的字母,按照代数式中的运算关系得出的结果.
和
单项式与多项式
二、同类项、合并同类项
1. 同类项:所含字母______,并且相同字母的指数也______的项叫作同类项.常数项与常数项也是同类项.
2. 合并同类项:把多项式中的同类项合并成一项,叫作合并同类项.
3. 合并同类项法则:同类项系数相加,所得结果作为系数,字母和字母的指数不变.
[注意] (1) 同类项不考虑字母的排列顺序,如-7xy 与 yx 是同类项;
(2) 只有同类项才能合并,如 x2+x3 不能合并.
相同
相同
三、去括号、添括号
1. 去括号法则:
(1)如果括号前面是“+”号,去括号时括号内的各项都不改变符号;
(2)如果括号前面是“-”号,去括号时括号内的各项都改变符号.
2. 添括号法则:
(1)如果所添括号前面是“+”号,括到括号内的各项都不改变符号;
(2)如果所添括号前面是“-”号,括到括号内的各项都改变符号.
三、整式加减
一般地,几个整式相加减,如果有括号就先________,然后再_____________.
运算结果,常将多项式按某个字母的次数从大到小(或从小到大)依次排列,这种排列叫作关于这个字母的降幂(升幂)排列.
去括号
合并同类项
考点一 整式的有关概念
例1 在 ,x + 1,-2, ,0.72xy, , 中单项
式的个数有 ( )
A. 2个 B. 3个 C. 4个 D. 5个
C
√
√
√
√
分析: 是除法形式,不是单项式,
是多项式.
1. (马尾期末) 下列说法正确的是 ( )
A. -3ab 的系数是 -3
B. 4a3b 的次数是 3
C. 2a + b - 1 的各项分别为 2a,b,1
D. 多项式 x2 - 1 是二次三项式
A
4
-
二次二项式
针对训练
考点二 同类项
例2 若 3xm+5y2 与 x3yn 的和是单项式,求 mn 的值.
【解析】由题意可知 3xm+5y2 与 x3yn 是同类项,所以 x 的指数和 y 的指数分别相等.
解:由题意得 m + 5 = 3,n = 2,所以 m =-2.
所以 mn=(-2)2=4.
2. (平凉期末) 如果单项式 3xa+3y2 与单项式 -4xyb-1 的和还是单项式,那么 ab 的值是 ( )
A. -6 B. -8 C. 8 D. -27
分析:单项式 + 单项式 = 单项式
可合并,即为同类项
所以 a + 3 = 1,b - 1 = 2,
所以 a = -2,b = 3,
所以 ab = -8.
B
针对训练
考点三 去括号、添括号
例3 已知 A=x3+2y3-xy2,B=-y3+x3+2xy2,
求:(1) A+B;(2) 2B-2A.
【解析】 把 A,B 所指的式子分别代入计算.
解:(1) A+B=(x3+2y3-xy2)+(-y3+x3+2xy2)
=x3+2y3-xy2-y3+x3+2xy2
=2x3+y3+xy2.
(2) 2B-2A=2(-y3+x3+2xy2)-2(x3+2y3-xy2)
=-2y3+2x3+4xy2-2x3-4y3+2xy2
=6xy2-6y3.
去括号是应注意:
(1)括号前是“-”号,去括号时括号里的各项要改变符号;
(2)运用乘法分配律时不要漏乘其中的项.
方法总结
3.下列各项中,去括号正确的是 ( )
A.x2-(2x-y+2)=x2-2x+y+2
B.-(m+n)-mn=-m+n-mn
C.x-(5x-3y)+(2x-y)=-2x+2y
D.ab-(-ab+3)=3
C
针对训练
4. (台江期末) 计算:
化简:
= -x - y.
解:原式
考点四 整式的加减运算与求值
在求多项式的值时,一般情况下是先化简,然后再把字母的值代入化简后的式子中求值,化简的过程就是整式运算的过程.
方法总结
5. (乐山期末) 已知 A = 3a2b - ab2,B = ab2 + 5a2b,
当 a = ,b = 时,求 5A - 3B 的值.
解:5A - 3B = 5(3a2b - ab2) - 3(ab2 + 5a2b)
= 15a2b - 5ab2 - 3ab2 - 15a2b
= -8ab2
当 x = ,y = 时,上式 .
针对训练
6. (兰州市期末) 已知多项式 M = (2x2 + 3xy + 2y) - 2(x2 + x + yx + 1).
(1) 当 x = 1,y = 2,求 M 的值;
(2) 若多项式 M 与字母 x 的取值无关,求 y 的值.
解:(1) M = (2x2 + 3xy + 2y) - 2(x2 + x + yx + 1)
= 2x2 + 3xy + 2y - 2x2 - 2x - 2yx - 2
= xy + 2y - 2x - 2.
当 x = 1,y = 2 时,M = 1×2 + 2×2 - 2×1 - 2 = 2.
(2) M = xy + 2y - 2x - 2 = (y - 2)x +2y -2.
因为多项式 M 与字母 x 无关,
所以 y - 2 = 0,y = 2.
例5 如图,用相同的小正方形按照某种规律进行摆放.根据图中小正方形的排列规律,猜想第 10 个图中小正方形的个数为 .
第 1 个图
第 2 个图
第 3 个图
第 4 个图
…
2 + 3×1
3 + 4×2
4 + 5×3
5 + 6×4
11 + 12×10
2×3 - 1
3×4 - 1
4×5 - 1
5×6 - 1
11×12 - 1
131
考点五 与整式的加减有关的探索性问题
7. (埇桥期末) 如图,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第 20 个图需要黑色棋子的个数为 .
3×1
4×2
5×3
6×4
22×20
440
针对训练
8. 用棋子摆出如图所示的一组 “口” 字,按照这种方法摆下去,则摆第 n 个 “口” 字需用棋子 ( )
A. 4n 枚 B. n2 枚 C. (4n - 4) 枚 D. (4n + 4) 枚
A
整 式 的 加 减
用字母表示数
单项式:
多项式:
去括号、添括号:
同类项:
合并同类项:
整式的加减:
系数、次数
项、次数、常数项
定义、“两相同、两无关”
定义、法则、步骤
法 则
步 骤
整式
七年级上册数学(沪科版)
小结与复习
第 2 章 整式及其加减
e7d195523061f1c0c2b73831c94a3edc981f60e396d3e182073EE1468018468A7F192AE5E5CD515B6C3125F8AF6E4EE646174E8CF0B46FD19828DCE8CDA3B3A044A74F0E769C5FA8CB87AB6FC303C8BA3785FAC64AF5424764E128FECAE4CC72932BB65C8C121A0F41C1707D94688ED66335DC6AE12288BF2055523C0C26863D2CD4AC454A29EEC183CEF0375334B579
代数式
整式
单项式
多项式
整式加减
合并同类项
去括号、添括号
一、整式的有关概念
1. 代数式:用加、减、乘、除及乘方等运算符号将数或表示数的字母连接而成的式子,叫作代数式. 单个的数或字母也是代数式.
2. 单项式:都是数与字母的____,这样的式子叫作单项式,单个的字母或数也是单项式.
3. 单项式的系数:单项式中的数字因数叫作这个单项式的系数.
4. 单项式的次数:一个单项式中,所有字母的指数的和叫作这个单项式的次数.
积
5. 多项式:几个单项式的____叫作多项式.
6. 多项式的项:多项式中,每个单项式(连同符号)叫做多项式的项.其中不含字母的项叫做常数项.一个多项式有几项,这个多项式就叫做几项式.
7. 多项式的次数:多项式里次数最高的项的次数,叫做这个多项式的次数.
8. 整式:____________________统称整式.
9. 代数式的值:用数字替代代数式里的字母,按照代数式中的运算关系得出的结果.
和
单项式与多项式
二、同类项、合并同类项
1. 同类项:所含字母______,并且相同字母的指数也______的项叫作同类项.常数项与常数项也是同类项.
2. 合并同类项:把多项式中的同类项合并成一项,叫作合并同类项.
3. 合并同类项法则:同类项系数相加,所得结果作为系数,字母和字母的指数不变.
[注意] (1) 同类项不考虑字母的排列顺序,如-7xy 与 yx 是同类项;
(2) 只有同类项才能合并,如 x2+x3 不能合并.
相同
相同
三、去括号、添括号
1. 去括号法则:
(1)如果括号前面是“+”号,去括号时括号内的各项都不改变符号;
(2)如果括号前面是“-”号,去括号时括号内的各项都改变符号.
2. 添括号法则:
(1)如果所添括号前面是“+”号,括到括号内的各项都不改变符号;
(2)如果所添括号前面是“-”号,括到括号内的各项都改变符号.
三、整式加减
一般地,几个整式相加减,如果有括号就先________,然后再_____________.
运算结果,常将多项式按某个字母的次数从大到小(或从小到大)依次排列,这种排列叫作关于这个字母的降幂(升幂)排列.
去括号
合并同类项
考点一 整式的有关概念
例1 在 ,x + 1,-2, ,0.72xy, , 中单项
式的个数有 ( )
A. 2个 B. 3个 C. 4个 D. 5个
C
√
√
√
√
分析: 是除法形式,不是单项式,
是多项式.
1. (马尾期末) 下列说法正确的是 ( )
A. -3ab 的系数是 -3
B. 4a3b 的次数是 3
C. 2a + b - 1 的各项分别为 2a,b,1
D. 多项式 x2 - 1 是二次三项式
A
4
-
二次二项式
针对训练
考点二 同类项
例2 若 3xm+5y2 与 x3yn 的和是单项式,求 mn 的值.
【解析】由题意可知 3xm+5y2 与 x3yn 是同类项,所以 x 的指数和 y 的指数分别相等.
解:由题意得 m + 5 = 3,n = 2,所以 m =-2.
所以 mn=(-2)2=4.
2. (平凉期末) 如果单项式 3xa+3y2 与单项式 -4xyb-1 的和还是单项式,那么 ab 的值是 ( )
A. -6 B. -8 C. 8 D. -27
分析:单项式 + 单项式 = 单项式
可合并,即为同类项
所以 a + 3 = 1,b - 1 = 2,
所以 a = -2,b = 3,
所以 ab = -8.
B
针对训练
考点三 去括号、添括号
例3 已知 A=x3+2y3-xy2,B=-y3+x3+2xy2,
求:(1) A+B;(2) 2B-2A.
【解析】 把 A,B 所指的式子分别代入计算.
解:(1) A+B=(x3+2y3-xy2)+(-y3+x3+2xy2)
=x3+2y3-xy2-y3+x3+2xy2
=2x3+y3+xy2.
(2) 2B-2A=2(-y3+x3+2xy2)-2(x3+2y3-xy2)
=-2y3+2x3+4xy2-2x3-4y3+2xy2
=6xy2-6y3.
去括号是应注意:
(1)括号前是“-”号,去括号时括号里的各项要改变符号;
(2)运用乘法分配律时不要漏乘其中的项.
方法总结
3.下列各项中,去括号正确的是 ( )
A.x2-(2x-y+2)=x2-2x+y+2
B.-(m+n)-mn=-m+n-mn
C.x-(5x-3y)+(2x-y)=-2x+2y
D.ab-(-ab+3)=3
C
针对训练
4. (台江期末) 计算:
化简:
= -x - y.
解:原式
考点四 整式的加减运算与求值
在求多项式的值时,一般情况下是先化简,然后再把字母的值代入化简后的式子中求值,化简的过程就是整式运算的过程.
方法总结
5. (乐山期末) 已知 A = 3a2b - ab2,B = ab2 + 5a2b,
当 a = ,b = 时,求 5A - 3B 的值.
解:5A - 3B = 5(3a2b - ab2) - 3(ab2 + 5a2b)
= 15a2b - 5ab2 - 3ab2 - 15a2b
= -8ab2
当 x = ,y = 时,上式 .
针对训练
6. (兰州市期末) 已知多项式 M = (2x2 + 3xy + 2y) - 2(x2 + x + yx + 1).
(1) 当 x = 1,y = 2,求 M 的值;
(2) 若多项式 M 与字母 x 的取值无关,求 y 的值.
解:(1) M = (2x2 + 3xy + 2y) - 2(x2 + x + yx + 1)
= 2x2 + 3xy + 2y - 2x2 - 2x - 2yx - 2
= xy + 2y - 2x - 2.
当 x = 1,y = 2 时,M = 1×2 + 2×2 - 2×1 - 2 = 2.
(2) M = xy + 2y - 2x - 2 = (y - 2)x +2y -2.
因为多项式 M 与字母 x 无关,
所以 y - 2 = 0,y = 2.
例5 如图,用相同的小正方形按照某种规律进行摆放.根据图中小正方形的排列规律,猜想第 10 个图中小正方形的个数为 .
第 1 个图
第 2 个图
第 3 个图
第 4 个图
…
2 + 3×1
3 + 4×2
4 + 5×3
5 + 6×4
11 + 12×10
2×3 - 1
3×4 - 1
4×5 - 1
5×6 - 1
11×12 - 1
131
考点五 与整式的加减有关的探索性问题
7. (埇桥期末) 如图,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第 20 个图需要黑色棋子的个数为 .
3×1
4×2
5×3
6×4
22×20
440
针对训练
8. 用棋子摆出如图所示的一组 “口” 字,按照这种方法摆下去,则摆第 n 个 “口” 字需用棋子 ( )
A. 4n 枚 B. n2 枚 C. (4n - 4) 枚 D. (4n + 4) 枚
A
整 式 的 加 减
用字母表示数
单项式:
多项式:
去括号、添括号:
同类项:
合并同类项:
整式的加减:
系数、次数
项、次数、常数项
定义、“两相同、两无关”
定义、法则、步骤
法 则
步 骤
整式
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
