2.2.1 合并同类项 课件(共22张PPT)2024-2025学年沪科版七年级数学上册
文档属性
| 名称 | 2.2.1 合并同类项 课件(共22张PPT)2024-2025学年沪科版七年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-12 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
七年级上册数学(沪科版)
2.2 整式加减
1. 合并同类项
第 2 章 整式及其加减
教学目标
1. 理解同类项的概念,掌握合并同类项的法则,能进行同类项的合并.
2. 通过对合并同类项的探究,学习类比的数学思想方法,发展探究能力,培养独立思考和合作交流的能力.
重点:同类项的概念、合并同类项的法则及应用.
难点:正确判断同类项;准确合并同类项.
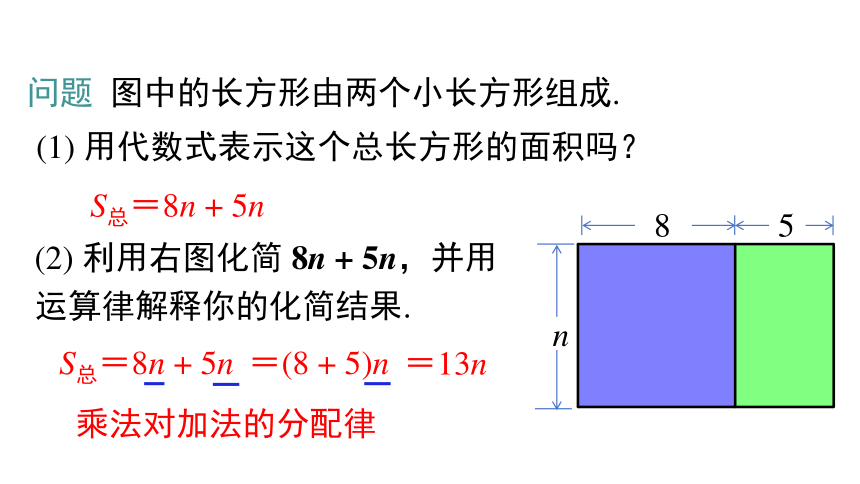
问题 图中的长方形由两个小长方形组成.
8
5
n
(1) 用代数式表示这个总长方形的面积吗?
S总=8n + 5n
(2) 利用右图化简 8n + 5n,并用运算律解释你的化简结果.
=(8 + 5)n
=13n
乘法对加法的分配律
S总=8n + 5n
1
同类项的概念
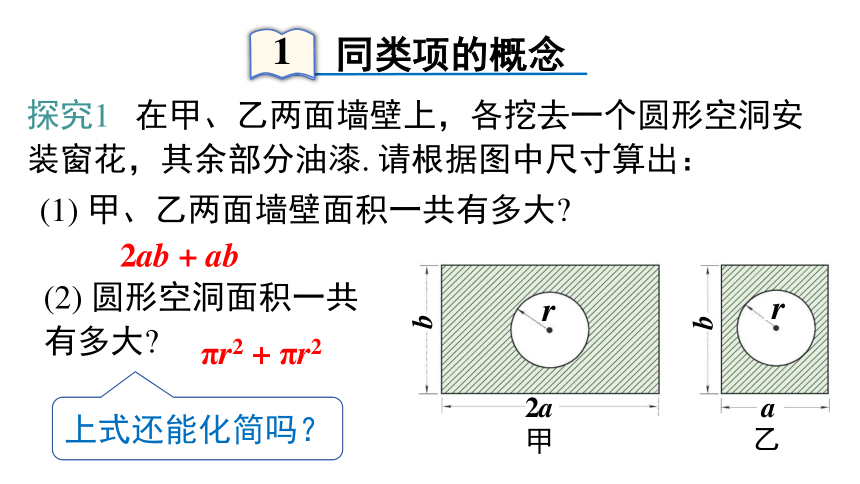
探究1 在甲、乙两面墙壁上,各挖去一个圆形空洞安装窗花,其余部分油漆. 请根据图中尺寸算出:
(1) 甲、乙两面墙壁面积一共有多大
(2) 圆形空洞面积一共有多大
r
2a
r
a
b
甲
乙
b
2ab + ab
πr2 + πr2
上式还能化简吗?
8n + 5n=(8 + 5)n=13n
2ab + ab =
根据乘法对加法的分配律:
(2 + 1)ab
=3ab
πr2 + πr2 =
(π + π)r2
=2πr2
观察等号左边的式子有什么共同特点,你能从中得出什么规律?
1. 多项式
2. 每项所含的字母相同
3. 相同字母的指数相同
所含 相同,并且相同字母的 也分别相同的项叫作同类项.
字母
指数
多项式中不含字母的常数项有同类项吗?
常数项与常数项是同类项.
同类项:
知识要点
3 和 0 互为同类项.
比如 3ab2 和 4ab2 互为同类项.
(3) -3pq 与 3qp
(1) 2x2y 与 -3x2y
(2) 2abc 与 3ab
(4) -4x2y 与 5xy2
例1 判断每一组是否是同类项,不是则为前者配一个。
√
×
3abc
√
×
5x2y
总结
同类项的判别方法:
只与字母及其指数有关,与系数无关,
与字母排列顺序无关.
典例精讲
练一练
2. 如果 2a2bn+1 与 -4amb3 是同类项,那么 m = ,
n = .
1. 在 6xy - 3x2 - 4x2y - 5yx2 + x2 中没有同类项的项是 .
6xy
2
2
合并同类项
2
探究2 计算:4x2 + 2x-1-3x2+3x+2.
解:原式=4x2-3x2 + 2x+3x-1+2
=(4x2-3x2) + (2x+3x)+[(-1)+2]
=(4-3)x2 + (2+3)x+(-1+2)
= x2 + 5x+1.
思考:每一步分别用了什么运算律?
交换律
结合律
分配律
合并同类项
合并同类项
把多项式中的同类项合并成 ,叫作合并同类项
一项
知识要点
同类项的系数 ,所得结果作为系数,字母和字母的 不变.
相加
指数
合并同类项法则:
两面墙上油漆面积一共有多大
问题 在甲、乙两面墙壁上,各挖去一个圆形空洞安装窗花,其余部分油漆. 请根据图中尺寸算出:
r
2a
r
a
b
甲
乙
b
S总=2ab + ab - (πr2 + πr2)
S总=2ab - πr2 + ab - πr2
=2ab + ab - πr2 - πr2
=3ab - 2πr2.
(1) 4a2 + 3b2 - 2ab + 3a2 + b2;
解 原式 = 4a2 - 3a2 - 2ab + 3b2 + b2
= a2 - 2ab + 4b2.
= (4 - 3)a2 - 2ab + (3 + 1)b2
①找出同类项
②用运算律将同类项移至一起
③合并同类项
例2 合并同类项:
典例精讲
(2) .
=
=
解
“合并同类项”的方法:
一找,找出多项式中的同类项,不同类的同类项用不同的标记标出;
二移,利用加法的交换律,将不同类的同类项分别集中;
三并,将同类项合并即可.
系数相加,字母及其指数不变
归纳总结
3.合并同类项:
(1) 6x+2x2-3x+x2+1;
(2) -3ab+7-2a2-9ab-3.
解:(1) 原式 = 6x-3x+2x2+x2+1
= 3x+3x2+1.
(2) 原式 = -3ab-9ab-2a2+7-3
=-12ab-2a2+4.
先分组,再合并
练一练
例3 求多项式 的值,其中
=
=
,b = 2,c = -3.
当
解
原式
①将多项式化简
②将数值代入化简后的式子
③计算结果
4. 在不知道 a,b 的情况下,能否求出“7a2-5b2+3a2b-4a2+b2-3a2b-3a2+4b2-2”的值,若能,请求出数值;若不能,请说明理由.
解:能.
化简 7a2-5b2+3a2b-4a2+b2-3a2b-3a2+4b2-2
= (7a2-4a2-3a2)+(-5b2+b2+4b2)+(3a2b-3a2b)-2
=-2,
所以,无论 a,b 取什么值,代数式的值都为 -2.
练一练
合并同类项的方法 ——
“一加二不变”
同类项的概念
与系数无关 (不为 0)
与所含字母的顺序无关
两无关
两同
相同字母的指数相同
所含字母相同
合并同类项
(1) 系数相加;
(2) 字母连同它的指数不变
1. 下列各组式子中是同类项的是( )
A.-2a 与 a2 B.2a2b 与 3ab2
C.5ab2c 与 -b2ac D.-ab2 和 4ab2c
2. 下列运算中正确的是( )
A.3a2 - 2a2 = a2 B.3a2 - 2a2 = 1
C.3x2 - x2 = 3 D.3x2 - x = 2x
C
A
3. 已知 与 能合并成一个单项式,则 m = ,n = .
4. 关于 a,b 的多项式
不含 ab 项,则 m = .
2
3
3
提示:能合并的两个(非 0)单项式一定是同类项.
提示:不含 ab 项,即多项式中 ab 项的系数为 0,或合并同类项后 ab 项的系数为 0. 所以 -6 + 2m = 0.
5. 求下列各式的值:
(1) 3a - 2b - 5a + b,其中 a = -3,b = 2;
(2) 3x3 - 2x2 + 5 - 3x3 - 2x2 + 1,其中 x = -0.5.
解:(1) 原式= (3 - 5) a + (-2 + 1) b = -2a - b.
当 a = -3,b = 2 时,上式= -2×(-3) - 2 = 4.
(2) 原式= (3 - 3) x3 + (-2 - 2) x2 + (5 + 1) = -4x2 + 6.
当 x = -0.5 时,上式= -4×(-0.5)2 + 6 = 5.
解:周长:5x + 2 + 3x2 + 7x -1
当 x = 2 时,周长: 3x2 + 12x + 1
6. 三角形三边长分别为 5x + 2,3x2,7x -1,则这个三角形的周长为多少?当 x = 2 时,周长为多少?
= 3x2 + (5x + 7x) + (2 - 1)
= 3x2 + 12x + 1
= 3×22 + 12×2 + 1
= 37
七年级上册数学(沪科版)
2.2 整式加减
1. 合并同类项
第 2 章 整式及其加减
教学目标
1. 理解同类项的概念,掌握合并同类项的法则,能进行同类项的合并.
2. 通过对合并同类项的探究,学习类比的数学思想方法,发展探究能力,培养独立思考和合作交流的能力.
重点:同类项的概念、合并同类项的法则及应用.
难点:正确判断同类项;准确合并同类项.
问题 图中的长方形由两个小长方形组成.
8
5
n
(1) 用代数式表示这个总长方形的面积吗?
S总=8n + 5n
(2) 利用右图化简 8n + 5n,并用运算律解释你的化简结果.
=(8 + 5)n
=13n
乘法对加法的分配律
S总=8n + 5n
1
同类项的概念
探究1 在甲、乙两面墙壁上,各挖去一个圆形空洞安装窗花,其余部分油漆. 请根据图中尺寸算出:
(1) 甲、乙两面墙壁面积一共有多大
(2) 圆形空洞面积一共有多大
r
2a
r
a
b
甲
乙
b
2ab + ab
πr2 + πr2
上式还能化简吗?
8n + 5n=(8 + 5)n=13n
2ab + ab =
根据乘法对加法的分配律:
(2 + 1)ab
=3ab
πr2 + πr2 =
(π + π)r2
=2πr2
观察等号左边的式子有什么共同特点,你能从中得出什么规律?
1. 多项式
2. 每项所含的字母相同
3. 相同字母的指数相同
所含 相同,并且相同字母的 也分别相同的项叫作同类项.
字母
指数
多项式中不含字母的常数项有同类项吗?
常数项与常数项是同类项.
同类项:
知识要点
3 和 0 互为同类项.
比如 3ab2 和 4ab2 互为同类项.
(3) -3pq 与 3qp
(1) 2x2y 与 -3x2y
(2) 2abc 与 3ab
(4) -4x2y 与 5xy2
例1 判断每一组是否是同类项,不是则为前者配一个。
√
×
3abc
√
×
5x2y
总结
同类项的判别方法:
只与字母及其指数有关,与系数无关,
与字母排列顺序无关.
典例精讲
练一练
2. 如果 2a2bn+1 与 -4amb3 是同类项,那么 m = ,
n = .
1. 在 6xy - 3x2 - 4x2y - 5yx2 + x2 中没有同类项的项是 .
6xy
2
2
合并同类项
2
探究2 计算:4x2 + 2x-1-3x2+3x+2.
解:原式=4x2-3x2 + 2x+3x-1+2
=(4x2-3x2) + (2x+3x)+[(-1)+2]
=(4-3)x2 + (2+3)x+(-1+2)
= x2 + 5x+1.
思考:每一步分别用了什么运算律?
交换律
结合律
分配律
合并同类项
合并同类项
把多项式中的同类项合并成 ,叫作合并同类项
一项
知识要点
同类项的系数 ,所得结果作为系数,字母和字母的 不变.
相加
指数
合并同类项法则:
两面墙上油漆面积一共有多大
问题 在甲、乙两面墙壁上,各挖去一个圆形空洞安装窗花,其余部分油漆. 请根据图中尺寸算出:
r
2a
r
a
b
甲
乙
b
S总=2ab + ab - (πr2 + πr2)
S总=2ab - πr2 + ab - πr2
=2ab + ab - πr2 - πr2
=3ab - 2πr2.
(1) 4a2 + 3b2 - 2ab + 3a2 + b2;
解 原式 = 4a2 - 3a2 - 2ab + 3b2 + b2
= a2 - 2ab + 4b2.
= (4 - 3)a2 - 2ab + (3 + 1)b2
①找出同类项
②用运算律将同类项移至一起
③合并同类项
例2 合并同类项:
典例精讲
(2) .
=
=
解
“合并同类项”的方法:
一找,找出多项式中的同类项,不同类的同类项用不同的标记标出;
二移,利用加法的交换律,将不同类的同类项分别集中;
三并,将同类项合并即可.
系数相加,字母及其指数不变
归纳总结
3.合并同类项:
(1) 6x+2x2-3x+x2+1;
(2) -3ab+7-2a2-9ab-3.
解:(1) 原式 = 6x-3x+2x2+x2+1
= 3x+3x2+1.
(2) 原式 = -3ab-9ab-2a2+7-3
=-12ab-2a2+4.
先分组,再合并
练一练
例3 求多项式 的值,其中
=
=
,b = 2,c = -3.
当
解
原式
①将多项式化简
②将数值代入化简后的式子
③计算结果
4. 在不知道 a,b 的情况下,能否求出“7a2-5b2+3a2b-4a2+b2-3a2b-3a2+4b2-2”的值,若能,请求出数值;若不能,请说明理由.
解:能.
化简 7a2-5b2+3a2b-4a2+b2-3a2b-3a2+4b2-2
= (7a2-4a2-3a2)+(-5b2+b2+4b2)+(3a2b-3a2b)-2
=-2,
所以,无论 a,b 取什么值,代数式的值都为 -2.
练一练
合并同类项的方法 ——
“一加二不变”
同类项的概念
与系数无关 (不为 0)
与所含字母的顺序无关
两无关
两同
相同字母的指数相同
所含字母相同
合并同类项
(1) 系数相加;
(2) 字母连同它的指数不变
1. 下列各组式子中是同类项的是( )
A.-2a 与 a2 B.2a2b 与 3ab2
C.5ab2c 与 -b2ac D.-ab2 和 4ab2c
2. 下列运算中正确的是( )
A.3a2 - 2a2 = a2 B.3a2 - 2a2 = 1
C.3x2 - x2 = 3 D.3x2 - x = 2x
C
A
3. 已知 与 能合并成一个单项式,则 m = ,n = .
4. 关于 a,b 的多项式
不含 ab 项,则 m = .
2
3
3
提示:能合并的两个(非 0)单项式一定是同类项.
提示:不含 ab 项,即多项式中 ab 项的系数为 0,或合并同类项后 ab 项的系数为 0. 所以 -6 + 2m = 0.
5. 求下列各式的值:
(1) 3a - 2b - 5a + b,其中 a = -3,b = 2;
(2) 3x3 - 2x2 + 5 - 3x3 - 2x2 + 1,其中 x = -0.5.
解:(1) 原式= (3 - 5) a + (-2 + 1) b = -2a - b.
当 a = -3,b = 2 时,上式= -2×(-3) - 2 = 4.
(2) 原式= (3 - 3) x3 + (-2 - 2) x2 + (5 + 1) = -4x2 + 6.
当 x = -0.5 时,上式= -4×(-0.5)2 + 6 = 5.
解:周长:5x + 2 + 3x2 + 7x -1
当 x = 2 时,周长: 3x2 + 12x + 1
6. 三角形三边长分别为 5x + 2,3x2,7x -1,则这个三角形的周长为多少?当 x = 2 时,周长为多少?
= 3x2 + (5x + 7x) + (2 - 1)
= 3x2 + 12x + 1
= 3×22 + 12×2 + 1
= 37
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
