2.7 角的和与差 课件(共52张PPT)2024-2025学年冀教版七年级数学上册
文档属性
| 名称 | 2.7 角的和与差 课件(共52张PPT)2024-2025学年冀教版七年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-12 20:16:12 | ||
图片预览







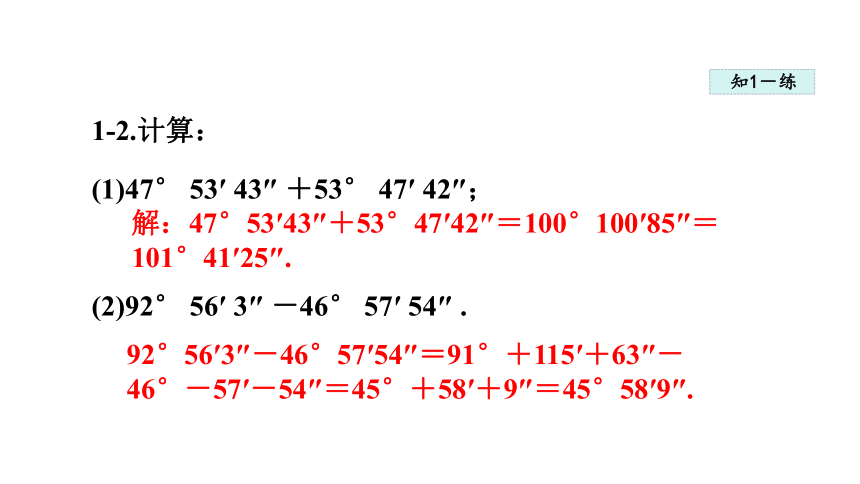



文档简介
(共52张PPT)
2.7 角的和与差
第二章 几何图形的初步认识
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
角的和、差
角平分线
余角和补角
余角、补角的性质
知1-讲
感悟新知
知识点
角的和、差
1
1. 角的和与差(数) 两个角的度数的和与差叫作这两个角的和与差 .
感悟新知
知1-讲
特别提醒
1. 两个角的和或差,仍然是一个角,角的和或差的度数,就是它们度数的和或差.
2. 在计算两个角的和或差时要将度与度、分与分、秒与秒分别相加或相减,分、秒相加时逢 60 要进位,相减时要借1当60.
感悟新知
2. 角的和与差(形)
知1-讲
文字描述 数学语言 图示
角的和 ∠ AOC 是 ∠ AOB与 ∠ BOC 的和 ∠ AOC= ∠ AOB+ ∠ BOC
角的差 ∠ AOB 是 ∠ AOC 与 ∠ COB 的差 ∠ AOB= ∠ AOC- ∠ COB
知1-练
感悟新知
[母题 教材 P87 例题 ]计算:
(1) 27° 26′ +53° 48′; (2) 90°-79° 18′ 6″;
(3) 18° 13′× 5; (4) 49° 28′ 52″ ÷ 4.
例1
解题秘方:利用有理数的运算法则结合角的单位的换算和进制进行计算 .
知1-练
感悟新知
解:27° 26′ +53° 48′ =80° 74′ =81° 14′ .
(1) 27° 26′ +53° 48′;
(2) 90°-79° 18′ 6″;
(3) 18° 13′× 5;
(4) 49° 28′ 52″ ÷ 4.
90°-79° 18′ 6″ =89° 59′ 60″ -79° 18′ 6″ =10° 41′ 54″ .
18° 13′ × 5=90° 65′ =91° 5′ .
49° 28′ 52″ ÷ 4=48° 88′ 52″ ÷ 4 =12° 22′ 13″ .
知1-练
感悟新知
1-1.若∠ 1+∠ 2=90°,∠ 1=58° 25′,则 ∠ 2的度数是( )
A.31° 75′ B.31° 35′
C. 41° 75′ D.41° 25′
B
知1-练
感悟新知
1-2.计算:
(1)47° 53′ 43″ +53° 47′ 42″;
(2)92° 56′ 3″ -46° 57′ 54″ .
解:47°53′43″+53°47′42″=100°100′85″=101°41′25″.
92°56′3″-46°57′54″=91°+115′+63″-46°-57′-54″=45°+58′+9″=45°58′9″.
知1-练
感悟新知
如图 2.7-1,回答下列问题:
(1) ∠ AOC 是哪两个角的和?
(2) ∠ AOB 是哪两个角的差?
(3) 如果∠ AOB= ∠ COD,那么∠ AOC 与∠ DOB 相等吗?
例2
知1-练
感悟新知
解:∠ AOC= ∠ AOB+ ∠ BOC.
解题秘方:根据图中角的位置关系得到角的和差关系 .
∠ AOB= ∠ AOD-∠ BOD= ∠ AOC-∠ BOC.
(1) ∠ AOC 是哪两个角的和?
(2) ∠ AOB 是哪两个角的差?
知1-练
感悟新知
解:∠ AOC= ∠ DOB.
因为∠ AOB= ∠ COD,
所以∠ AOB+ ∠ BOC= ∠ COD+ ∠ BOC,
即∠ AOC= ∠ DOB.
(3) 如果∠ AOB= ∠ COD,那么∠ AOC 与∠ DOB 相等吗?
在等式的两边分别加上相
等的量,所得结果仍是等式.
知1-练
感悟新知
2-1.在所给的:①15°,②65°,③75°,④ 135°,⑤ 145° 角度中,可以用一副三角尺画出来的是( )
A. ②④⑤ B. ①②④
C. ①③⑤ D. ①③④
D
感悟新知
知2-讲
知识点
角平分线
2
1. 定义 如果从一个角的顶点引出的一条射线把这个角分成的两个角相等,那么这条射线叫作这个角的角平分线 .
感悟新知
知2-讲
表示方法:如图2.7-2,若OC平分∠ AOB,则∠ AOC=
∠ BOC= ∠ AOB, 2 ∠ AOC=2 ∠ BOC=
∠ AOB; 反之,若∠ AOC= ∠ BOC= ∠ AOB,
2∠ AOC=2∠ BOC=∠ AOB,则OC平分∠ AOB.
感悟新知
知2-讲
2. 角的 n 等分线(拓展) 类似角的平分线,从角的顶点引出的射线,将角分成相等的 n 个角,叫作角的 n 等分线,例如角的三等分线、四等分线等 .
3. 角的平分线的作法 (1) 用量角器来画;(2) 通过折叠,使角的两边重合,沿折痕画射线,这条射线即为这个角的角平分线 .
知2-讲
感悟新知
特别提醒
1.角平分线的“三要素”:
(1) 是从角的顶点引出的射线;
(2)在角的内部;
(3)将已知角平分.
2. 角的平分线只有一条.
感悟新知
知2-练
[期末·石家庄裕华区]如图 2.7-3,∠ AOC=90°, OC 平分∠ DOB,∠ DOC=25° 35′,求∠ BOA 的度数.
例3
知2-练
感悟新知
解题秘方:先利用角平分线的定义求出∠ BOC 的度数,再求∠ BOA 的度数.
解:因为OC平分∠ DOB,
所以∠ BOC= ∠ DOC=25° 35′.
又因为∠ AOC=90° ,
所以∠ BOA= ∠ AOC - ∠ BOC=90° -
25° 35′ =64° 25′.
知2-练
感悟新知
3-1. [期末· 廊坊]如图, OC 是 ∠ AOD 的 平分线, OE是∠ BOD的平分线,∠ AOB=130° .
(1) 若∠ BOE=45°,求∠ AOC 的度数;
知2-练
感悟新知
(2)求∠ COE 的度数 .
感悟新知
知2-练
[母题 教材 P89 习题 T6 ]如图 2.7-4, O 为直线 AB 上 一点,∠ AOC=50°, OD 平分∠ AOC,
∠ EOD=90° .
(1) 求∠ BOD 的度数;
(2)小明发现 OE 平分 ∠ BOC,请你通过计算说明理由 .
例4
知2-练
感悟新知
(1) 求∠ BOD 的度数;
解:因为∠ AOC=50° , OD 平分∠ AOC,
所以∠ DOC= ∠ AOC=25° ,
∠ BOC=180° - ∠ AOC=180° - 50° =130° .
所以∠ BOD= ∠ BOC+ ∠ DOC=130° +25°=155° .
解题秘方:利用∠ BOD= ∠ BOC+ ∠ DOC 求解即可;
知2-练
感悟新知
(2)小明发现 OE 平分 ∠ BOC,请你通过计算说明理由 .
解: 因为∠ DOE=90° , ∠ DOC=25° ,
所以∠ COE= ∠ DOE - ∠ DOC=90° - 25° =65° .
又因为∠ BOE= ∠ BOD - ∠ DOE=155° - 90° =65° ,
所以∠ COE= ∠ BOE,即 OE 平分∠ BOC.
解题秘方: 分别求出∠ COE 和∠ BOE 的度数即可 .
知2-练
感悟新知
4-1.如图,点 A, O, B在同一条直线上, ∠ BOC=78°,∠ DOE=77°, OD 是 ∠ BOC 的一条靠近 OC 边的三等分线.
(1)求∠ COE 的度数.
知2-练
感悟新知
知2-练
感悟新知
(2)OE 是∠ AOC 的平分线吗?说明你的理由.
解:OE是∠AOC的平分线.
理由:因为∠COE=51°,∠BOC=78°,
所以∠AOE=180°-∠COE-∠BOC=
180°-51°-78°=51°.
所以∠AOE=∠COE,
所以OE是∠AOC的平分线.
感悟新知
知3-讲
知识点
余角和补角
3
1. 余角 如果 ∠ α+ ∠ β=90 ° ,那么我们就称 ∠ α 与 ∠ β 互为余角,简称互余 . 其中, ∠ α(∠ β)叫作∠ β(∠ α) 的余角 .
数学语言:如图 2.7-5,如果 ∠ 1+ ∠ 2=90 ° ,就 说
∠ 1 是∠ 2 的余角,或∠ 1 与∠ 2 互为余角 .
感悟新知
知3-讲
2. 补角 如果∠ α+ ∠ β=180° ,那么我们就称∠ α 与∠β 互为补角,简称互补 . 其中, ∠ α(∠ β) 叫作∠ β(∠α) 的补角 .
数学语言:如图 2.7-6,如 果 ∠ 3+ ∠ 4=180 ° ,就 说∠ 3 是∠ 4 的补角,或∠ 3 与∠ 4 互为补角 .
感悟新知
知3-讲
3. 邻补角 两个角有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角称为邻补角 . 如图 2.7-7, ∠ AOB 与∠ BOC 互为邻补角 .
知3-讲
感悟新知
特别解读
1. 互余、互补是指两个角之间的数量关系,它们是成对出现的.
2. 若两个角互余,则两个角都是锐角;若两个角互补,则两个角可能都是直角,也可能一个角是锐角,另 一个角是钝角.
3. 互余、互补只与数量有关,与位置无关,若将直角分成两个角,则这两个角互余,若将平角分成两个角,则这两个角互补.
知3-练
感悟新知
一个角的补角为 138°,则这个角的余角为( )
A.38° B.42° C.48° D.132°
例5
知3-练
感悟新知
解题秘方:紧扣余角和补角的定义进行角的和差的计算即可.
解:这个角是 180° - 138° =42° ,
所以这个角的余角是 90° - 42° =48° .
答案:C
知3-练
感悟新知
5-1. [期 末· 邯 郸]如果一个角与它的余角的度数之比为1∶ 2,则这个角是 _____度,这个角的补角与它的余角的差等于 _______度.
30
90
知3-练
感悟新知
如图 2.7-8,点 O 为直线 AB 上一点,
∠ AOC= ∠ DOE=90° .
(1)图中互余的角有几对?各是哪些?
(2) 图中互补的角有几对?各是哪些?
例6
解题秘方:紧扣余角、补角的定义解答 .
知3-练
感悟新知
(1)图中互余的角有几对?各是哪些?
解:因为点 O 为直线 AB 上一点,
所以∠ BOC+ ∠ AOC=180°(平角的定义) .
因为∠ AOC=90° ,所以∠ BOC=180°-
∠ AOC=90° ,又因为∠ DOE=90° ,
所 以 ∠ 1+ ∠ 2=90 ° , ∠ 2+ ∠ 3=90 ° ,
∠ 3+ ∠ 4=90 ° ,∠ 1+ ∠ 4=90° ,
所以图中互余的角有 4 对,分别是 ∠ 1 和 ∠ 2,
∠ 2 和∠ 3, ∠ 3 和∠ 4, ∠ 1 和∠ 4.
知3-练
感悟新知
(2) 图中互补的角有几对?各是哪些?
解:由题意得∠ 1+ ∠ BOD=180° , ∠ 4+ ∠ AOE=180° ,由(1) 易知∠ 1= ∠ 3, ∠ 2= ∠ 4,
所以∠ 3+ ∠ BOD=180° , ∠ 2+ ∠ AOE=180° .
又因为∠ AOC+ ∠ BOC=180° , ∠ AOC+ ∠ DOE=180° ,∠ DOE+ ∠ BOC=180° ,
所以图中互补的角有 7 对,分别是∠ 1 和∠ BOD,
∠ 4 和∠ AOE, ∠ 3 和 ∠ BOD, ∠ 2 和 ∠ AOE, ∠ AOC 和 ∠ BOC,∠ AOC 和∠ DOE, ∠ DOE 和∠ BOC.
知3-练
感悟新知
6-1.如图,直线 AB,CD相交于点O, ∠ AOE=∠COF=90 °,则 图中 与 ∠ BOC 互补的角有( )
A.1个 B.2个
C.3 个 D.4个
C
知3-练
感悟新知
6-2.如图,点 O 为 直线 BE 上一点,∠ AOE= ∠ COD=90 °,则图中与∠ BOC 互余的角有( )
A.1个 B.2个
C.3 个 D.4个
B
感悟新知
知4-讲
知识点
余角、补角的性质
4
1. 余角的性质
(1) 同角的余角相等 .
如果∠ 1+ ∠ 2=90° , ∠ 1+ ∠ 3=90° ,那么∠ 2= ∠ 3.
(2) 等角的余角相等 .
如果∠ 1+ ∠ 2=90° , ∠ 3+ ∠ 4=90° ,且∠ 1= ∠ 3,
那么∠ 2= ∠ 4.
同一个角.
度数相等的角.
感悟新知
知4-讲
2. 补角的性质
(1) 同角的补角相等 .
如果∠ 1+ ∠ 2=180° , ∠ 1+ ∠ 3=180° ,那么∠ 2= ∠ 3.
(2) 等角的补角相等 .
如果∠ 1+ ∠ 2=180° , ∠ 3+ ∠ 4=180° ,且∠ 1= ∠ 3,
那么∠ 2= ∠ 4.
知4-讲
感悟新知
特别提醒
◆如果互补的两个角相等,那么这两个角都是直角.
◆余角、补角的性质是说明两个角相等的重要依据.
感悟新知
知4-练
如图 2.7-9,已知 O 是直线 AB 上的一点, OC 是一条射线, OD 平分∠ AOC,∠ DOE=90°,则 OE 平分∠ BOC 吗?为什么?
例7
知4-练
感悟新知
解题秘方:紧扣角平分线的定义,利用余角的性质说明两个角相等 .
知4-练
感悟新知
解:OE 平分∠ BOC. 理由如下:
因为∠ DOE=90° ,所以∠ DOC+ ∠ COE=90° .
又因为∠ AOB=180° ,所以∠ AOD+ ∠ BOE=90° .
因为 OD 平分∠ AOC,所以∠ AOD= ∠ DOC.
所以∠ COE= ∠ BOE. 所以 OE 平分∠ BOC.
知4-练
感悟新知
7-1. [期末· 台州]如图,点 O 在直线 AE 上, ∠ AOB=∠ COD=90°,则图中除了直角外,一定相等的角有( )
A.3对 B.2对
C.1 对 D.0对
B
感悟新知
知4-练
如图 2.7-10,直线 AB 与∠ COD 的两边OC, OD 分别相交于点 E, F,∠ 1+ ∠ 2=180° .
找出图中与∠ 2 相等的角,并说明理由 .
例8
解题秘方:利用补角的性质找出与∠ 2 相等的角 .
知4-练
感悟新知
解:因为∠ 1+ ∠ 3=180° , ∠ 1+ ∠ 2=180° ,
所以∠ 3= ∠ 2.
因为∠ 1+ ∠ 4=180° , ∠ 1+ ∠ 2=180° ,所以∠ 4= ∠ 2.
因为∠ 2+ ∠ 5=180° , ∠ 6+ ∠ 5=180° ,所以∠ 2= ∠ 6.
所以图中与∠ 2 相等的角有∠ 3, ∠ 4, ∠ 6.
同角的补角相等
知4-练
感悟新知
8-1.如图,点 O 在直线AB上,∠ BOC=90°,∠ BOD和∠ COD互补.
(1)请说明∠ AOD=∠ COD;
知4-练
感悟新知
解:因为∠BOD和∠COD互补,
所以∠BOD+∠COD=180°.
因为点O在直线AB上,所以∠AOB=180°.
所以∠BOD+∠AOD=180°.
所以∠AOD=∠COD.(同角的补角相等)
知4-练
感悟新知
(2)求∠ AOD 的度数.
角的和与差
角的和与差
余角和补角
两个角
性质
角平分线
2.7 角的和与差
第二章 几何图形的初步认识
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
角的和、差
角平分线
余角和补角
余角、补角的性质
知1-讲
感悟新知
知识点
角的和、差
1
1. 角的和与差(数) 两个角的度数的和与差叫作这两个角的和与差 .
感悟新知
知1-讲
特别提醒
1. 两个角的和或差,仍然是一个角,角的和或差的度数,就是它们度数的和或差.
2. 在计算两个角的和或差时要将度与度、分与分、秒与秒分别相加或相减,分、秒相加时逢 60 要进位,相减时要借1当60.
感悟新知
2. 角的和与差(形)
知1-讲
文字描述 数学语言 图示
角的和 ∠ AOC 是 ∠ AOB与 ∠ BOC 的和 ∠ AOC= ∠ AOB+ ∠ BOC
角的差 ∠ AOB 是 ∠ AOC 与 ∠ COB 的差 ∠ AOB= ∠ AOC- ∠ COB
知1-练
感悟新知
[母题 教材 P87 例题 ]计算:
(1) 27° 26′ +53° 48′; (2) 90°-79° 18′ 6″;
(3) 18° 13′× 5; (4) 49° 28′ 52″ ÷ 4.
例1
解题秘方:利用有理数的运算法则结合角的单位的换算和进制进行计算 .
知1-练
感悟新知
解:27° 26′ +53° 48′ =80° 74′ =81° 14′ .
(1) 27° 26′ +53° 48′;
(2) 90°-79° 18′ 6″;
(3) 18° 13′× 5;
(4) 49° 28′ 52″ ÷ 4.
90°-79° 18′ 6″ =89° 59′ 60″ -79° 18′ 6″ =10° 41′ 54″ .
18° 13′ × 5=90° 65′ =91° 5′ .
49° 28′ 52″ ÷ 4=48° 88′ 52″ ÷ 4 =12° 22′ 13″ .
知1-练
感悟新知
1-1.若∠ 1+∠ 2=90°,∠ 1=58° 25′,则 ∠ 2的度数是( )
A.31° 75′ B.31° 35′
C. 41° 75′ D.41° 25′
B
知1-练
感悟新知
1-2.计算:
(1)47° 53′ 43″ +53° 47′ 42″;
(2)92° 56′ 3″ -46° 57′ 54″ .
解:47°53′43″+53°47′42″=100°100′85″=101°41′25″.
92°56′3″-46°57′54″=91°+115′+63″-46°-57′-54″=45°+58′+9″=45°58′9″.
知1-练
感悟新知
如图 2.7-1,回答下列问题:
(1) ∠ AOC 是哪两个角的和?
(2) ∠ AOB 是哪两个角的差?
(3) 如果∠ AOB= ∠ COD,那么∠ AOC 与∠ DOB 相等吗?
例2
知1-练
感悟新知
解:∠ AOC= ∠ AOB+ ∠ BOC.
解题秘方:根据图中角的位置关系得到角的和差关系 .
∠ AOB= ∠ AOD-∠ BOD= ∠ AOC-∠ BOC.
(1) ∠ AOC 是哪两个角的和?
(2) ∠ AOB 是哪两个角的差?
知1-练
感悟新知
解:∠ AOC= ∠ DOB.
因为∠ AOB= ∠ COD,
所以∠ AOB+ ∠ BOC= ∠ COD+ ∠ BOC,
即∠ AOC= ∠ DOB.
(3) 如果∠ AOB= ∠ COD,那么∠ AOC 与∠ DOB 相等吗?
在等式的两边分别加上相
等的量,所得结果仍是等式.
知1-练
感悟新知
2-1.在所给的:①15°,②65°,③75°,④ 135°,⑤ 145° 角度中,可以用一副三角尺画出来的是( )
A. ②④⑤ B. ①②④
C. ①③⑤ D. ①③④
D
感悟新知
知2-讲
知识点
角平分线
2
1. 定义 如果从一个角的顶点引出的一条射线把这个角分成的两个角相等,那么这条射线叫作这个角的角平分线 .
感悟新知
知2-讲
表示方法:如图2.7-2,若OC平分∠ AOB,则∠ AOC=
∠ BOC= ∠ AOB, 2 ∠ AOC=2 ∠ BOC=
∠ AOB; 反之,若∠ AOC= ∠ BOC= ∠ AOB,
2∠ AOC=2∠ BOC=∠ AOB,则OC平分∠ AOB.
感悟新知
知2-讲
2. 角的 n 等分线(拓展) 类似角的平分线,从角的顶点引出的射线,将角分成相等的 n 个角,叫作角的 n 等分线,例如角的三等分线、四等分线等 .
3. 角的平分线的作法 (1) 用量角器来画;(2) 通过折叠,使角的两边重合,沿折痕画射线,这条射线即为这个角的角平分线 .
知2-讲
感悟新知
特别提醒
1.角平分线的“三要素”:
(1) 是从角的顶点引出的射线;
(2)在角的内部;
(3)将已知角平分.
2. 角的平分线只有一条.
感悟新知
知2-练
[期末·石家庄裕华区]如图 2.7-3,∠ AOC=90°, OC 平分∠ DOB,∠ DOC=25° 35′,求∠ BOA 的度数.
例3
知2-练
感悟新知
解题秘方:先利用角平分线的定义求出∠ BOC 的度数,再求∠ BOA 的度数.
解:因为OC平分∠ DOB,
所以∠ BOC= ∠ DOC=25° 35′.
又因为∠ AOC=90° ,
所以∠ BOA= ∠ AOC - ∠ BOC=90° -
25° 35′ =64° 25′.
知2-练
感悟新知
3-1. [期末· 廊坊]如图, OC 是 ∠ AOD 的 平分线, OE是∠ BOD的平分线,∠ AOB=130° .
(1) 若∠ BOE=45°,求∠ AOC 的度数;
知2-练
感悟新知
(2)求∠ COE 的度数 .
感悟新知
知2-练
[母题 教材 P89 习题 T6 ]如图 2.7-4, O 为直线 AB 上 一点,∠ AOC=50°, OD 平分∠ AOC,
∠ EOD=90° .
(1) 求∠ BOD 的度数;
(2)小明发现 OE 平分 ∠ BOC,请你通过计算说明理由 .
例4
知2-练
感悟新知
(1) 求∠ BOD 的度数;
解:因为∠ AOC=50° , OD 平分∠ AOC,
所以∠ DOC= ∠ AOC=25° ,
∠ BOC=180° - ∠ AOC=180° - 50° =130° .
所以∠ BOD= ∠ BOC+ ∠ DOC=130° +25°=155° .
解题秘方:利用∠ BOD= ∠ BOC+ ∠ DOC 求解即可;
知2-练
感悟新知
(2)小明发现 OE 平分 ∠ BOC,请你通过计算说明理由 .
解: 因为∠ DOE=90° , ∠ DOC=25° ,
所以∠ COE= ∠ DOE - ∠ DOC=90° - 25° =65° .
又因为∠ BOE= ∠ BOD - ∠ DOE=155° - 90° =65° ,
所以∠ COE= ∠ BOE,即 OE 平分∠ BOC.
解题秘方: 分别求出∠ COE 和∠ BOE 的度数即可 .
知2-练
感悟新知
4-1.如图,点 A, O, B在同一条直线上, ∠ BOC=78°,∠ DOE=77°, OD 是 ∠ BOC 的一条靠近 OC 边的三等分线.
(1)求∠ COE 的度数.
知2-练
感悟新知
知2-练
感悟新知
(2)OE 是∠ AOC 的平分线吗?说明你的理由.
解:OE是∠AOC的平分线.
理由:因为∠COE=51°,∠BOC=78°,
所以∠AOE=180°-∠COE-∠BOC=
180°-51°-78°=51°.
所以∠AOE=∠COE,
所以OE是∠AOC的平分线.
感悟新知
知3-讲
知识点
余角和补角
3
1. 余角 如果 ∠ α+ ∠ β=90 ° ,那么我们就称 ∠ α 与 ∠ β 互为余角,简称互余 . 其中, ∠ α(∠ β)叫作∠ β(∠ α) 的余角 .
数学语言:如图 2.7-5,如果 ∠ 1+ ∠ 2=90 ° ,就 说
∠ 1 是∠ 2 的余角,或∠ 1 与∠ 2 互为余角 .
感悟新知
知3-讲
2. 补角 如果∠ α+ ∠ β=180° ,那么我们就称∠ α 与∠β 互为补角,简称互补 . 其中, ∠ α(∠ β) 叫作∠ β(∠α) 的补角 .
数学语言:如图 2.7-6,如 果 ∠ 3+ ∠ 4=180 ° ,就 说∠ 3 是∠ 4 的补角,或∠ 3 与∠ 4 互为补角 .
感悟新知
知3-讲
3. 邻补角 两个角有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角称为邻补角 . 如图 2.7-7, ∠ AOB 与∠ BOC 互为邻补角 .
知3-讲
感悟新知
特别解读
1. 互余、互补是指两个角之间的数量关系,它们是成对出现的.
2. 若两个角互余,则两个角都是锐角;若两个角互补,则两个角可能都是直角,也可能一个角是锐角,另 一个角是钝角.
3. 互余、互补只与数量有关,与位置无关,若将直角分成两个角,则这两个角互余,若将平角分成两个角,则这两个角互补.
知3-练
感悟新知
一个角的补角为 138°,则这个角的余角为( )
A.38° B.42° C.48° D.132°
例5
知3-练
感悟新知
解题秘方:紧扣余角和补角的定义进行角的和差的计算即可.
解:这个角是 180° - 138° =42° ,
所以这个角的余角是 90° - 42° =48° .
答案:C
知3-练
感悟新知
5-1. [期 末· 邯 郸]如果一个角与它的余角的度数之比为1∶ 2,则这个角是 _____度,这个角的补角与它的余角的差等于 _______度.
30
90
知3-练
感悟新知
如图 2.7-8,点 O 为直线 AB 上一点,
∠ AOC= ∠ DOE=90° .
(1)图中互余的角有几对?各是哪些?
(2) 图中互补的角有几对?各是哪些?
例6
解题秘方:紧扣余角、补角的定义解答 .
知3-练
感悟新知
(1)图中互余的角有几对?各是哪些?
解:因为点 O 为直线 AB 上一点,
所以∠ BOC+ ∠ AOC=180°(平角的定义) .
因为∠ AOC=90° ,所以∠ BOC=180°-
∠ AOC=90° ,又因为∠ DOE=90° ,
所 以 ∠ 1+ ∠ 2=90 ° , ∠ 2+ ∠ 3=90 ° ,
∠ 3+ ∠ 4=90 ° ,∠ 1+ ∠ 4=90° ,
所以图中互余的角有 4 对,分别是 ∠ 1 和 ∠ 2,
∠ 2 和∠ 3, ∠ 3 和∠ 4, ∠ 1 和∠ 4.
知3-练
感悟新知
(2) 图中互补的角有几对?各是哪些?
解:由题意得∠ 1+ ∠ BOD=180° , ∠ 4+ ∠ AOE=180° ,由(1) 易知∠ 1= ∠ 3, ∠ 2= ∠ 4,
所以∠ 3+ ∠ BOD=180° , ∠ 2+ ∠ AOE=180° .
又因为∠ AOC+ ∠ BOC=180° , ∠ AOC+ ∠ DOE=180° ,∠ DOE+ ∠ BOC=180° ,
所以图中互补的角有 7 对,分别是∠ 1 和∠ BOD,
∠ 4 和∠ AOE, ∠ 3 和 ∠ BOD, ∠ 2 和 ∠ AOE, ∠ AOC 和 ∠ BOC,∠ AOC 和∠ DOE, ∠ DOE 和∠ BOC.
知3-练
感悟新知
6-1.如图,直线 AB,CD相交于点O, ∠ AOE=∠COF=90 °,则 图中 与 ∠ BOC 互补的角有( )
A.1个 B.2个
C.3 个 D.4个
C
知3-练
感悟新知
6-2.如图,点 O 为 直线 BE 上一点,∠ AOE= ∠ COD=90 °,则图中与∠ BOC 互余的角有( )
A.1个 B.2个
C.3 个 D.4个
B
感悟新知
知4-讲
知识点
余角、补角的性质
4
1. 余角的性质
(1) 同角的余角相等 .
如果∠ 1+ ∠ 2=90° , ∠ 1+ ∠ 3=90° ,那么∠ 2= ∠ 3.
(2) 等角的余角相等 .
如果∠ 1+ ∠ 2=90° , ∠ 3+ ∠ 4=90° ,且∠ 1= ∠ 3,
那么∠ 2= ∠ 4.
同一个角.
度数相等的角.
感悟新知
知4-讲
2. 补角的性质
(1) 同角的补角相等 .
如果∠ 1+ ∠ 2=180° , ∠ 1+ ∠ 3=180° ,那么∠ 2= ∠ 3.
(2) 等角的补角相等 .
如果∠ 1+ ∠ 2=180° , ∠ 3+ ∠ 4=180° ,且∠ 1= ∠ 3,
那么∠ 2= ∠ 4.
知4-讲
感悟新知
特别提醒
◆如果互补的两个角相等,那么这两个角都是直角.
◆余角、补角的性质是说明两个角相等的重要依据.
感悟新知
知4-练
如图 2.7-9,已知 O 是直线 AB 上的一点, OC 是一条射线, OD 平分∠ AOC,∠ DOE=90°,则 OE 平分∠ BOC 吗?为什么?
例7
知4-练
感悟新知
解题秘方:紧扣角平分线的定义,利用余角的性质说明两个角相等 .
知4-练
感悟新知
解:OE 平分∠ BOC. 理由如下:
因为∠ DOE=90° ,所以∠ DOC+ ∠ COE=90° .
又因为∠ AOB=180° ,所以∠ AOD+ ∠ BOE=90° .
因为 OD 平分∠ AOC,所以∠ AOD= ∠ DOC.
所以∠ COE= ∠ BOE. 所以 OE 平分∠ BOC.
知4-练
感悟新知
7-1. [期末· 台州]如图,点 O 在直线 AE 上, ∠ AOB=∠ COD=90°,则图中除了直角外,一定相等的角有( )
A.3对 B.2对
C.1 对 D.0对
B
感悟新知
知4-练
如图 2.7-10,直线 AB 与∠ COD 的两边OC, OD 分别相交于点 E, F,∠ 1+ ∠ 2=180° .
找出图中与∠ 2 相等的角,并说明理由 .
例8
解题秘方:利用补角的性质找出与∠ 2 相等的角 .
知4-练
感悟新知
解:因为∠ 1+ ∠ 3=180° , ∠ 1+ ∠ 2=180° ,
所以∠ 3= ∠ 2.
因为∠ 1+ ∠ 4=180° , ∠ 1+ ∠ 2=180° ,所以∠ 4= ∠ 2.
因为∠ 2+ ∠ 5=180° , ∠ 6+ ∠ 5=180° ,所以∠ 2= ∠ 6.
所以图中与∠ 2 相等的角有∠ 3, ∠ 4, ∠ 6.
同角的补角相等
知4-练
感悟新知
8-1.如图,点 O 在直线AB上,∠ BOC=90°,∠ BOD和∠ COD互补.
(1)请说明∠ AOD=∠ COD;
知4-练
感悟新知
解:因为∠BOD和∠COD互补,
所以∠BOD+∠COD=180°.
因为点O在直线AB上,所以∠AOB=180°.
所以∠BOD+∠AOD=180°.
所以∠AOD=∠COD.(同角的补角相等)
知4-练
感悟新知
(2)求∠ AOD 的度数.
角的和与差
角的和与差
余角和补角
两个角
性质
角平分线
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
