2.1 代数式 课件(共76张PPT)2024-2025学年新沪科版七年级数学上册
文档属性
| 名称 | 2.1 代数式 课件(共76张PPT)2024-2025学年新沪科版七年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-12 20:19:54 | ||
图片预览











文档简介
(共76张PPT)
2.1 代数式
第二章 整式及其加减
学习目标
课时讲解
1
用字母表示数
代数式
列代数式
单项式
多项式
整式
代数式的值
逐点
导讲练
课堂小结
作业提升
学习目标
课时流程
2
知1-讲
感悟新知
知识点
用字母表示数
1
1. 用字母表示数 用字母或含有字母的式子表示数或数量关系 . 在用字母表示数中,字母和数一样可以参与运算,可以用式子把数量关系简明地表示出来 .
感悟新知
知1-讲
特别提醒
同一问题中,相同的字母必须表示相同的量,不同的量必须用不同的字母表示.
感悟新知
2. 用字母表示数具有如下特点
(1) 任意性:字母可以表示任意的数 .
(2) 限制性:字母的取值必须使式子有意义且符合实际情况 .
(3) 确定性:字母的取值一旦确定,式子的值也随之确定 .
(4) 一般性:用字母表示数能更准确地反映事物的规律,更具有一般性 .
知1-讲
知1-练
感悟新知
[母题 教材 P63 练习 T2] 填空:
(1)买单价为 6 元的钢笔 a 支,共需 ______元;
(2) 一台电视机的标价为 a 元,则 打 八 折 后 的 售价为______元;
例1
6a
0.8a
解题秘方:类比用具体数表示数量关系的方式,用字母表示数量关系 .
知1-练
感悟新知
1-1.[期中·北京朝阳区]一种商品每件盈利a 元,售出 60 件,共盈利_________元(用含 a的式子表示).
60a
知1-练
感悟新知
填空:
(1)三个连续偶数,若中间一个数为 2n,则其余两个数分别为 ______________;
(2)若一个两位数,其个位数字为 a,十位数字为 b,则这个两位数为 _________.
例2
2n-2, 2n+2
解题秘方:紧扣各类数的特征,用字母表示这些特征数 .
10b+a
知1-练
感悟新知
2-1.若 m 表示一个两位数, n 表示一个三位数.把 m 写在 n 的右侧组成一个五位数,则能表示这个五位数的式子是( )
A. mn
B. 100m+n
C. 100n+m
D. 1 000n+100m
C
知1-练
感悟新知
2-2.两个连续奇数中,设较大的一个数为x,那么另 一个数为( )
A. x+1 B. x+2
C. 2x+1 D. x - 2
D
知1-练
感悟新知
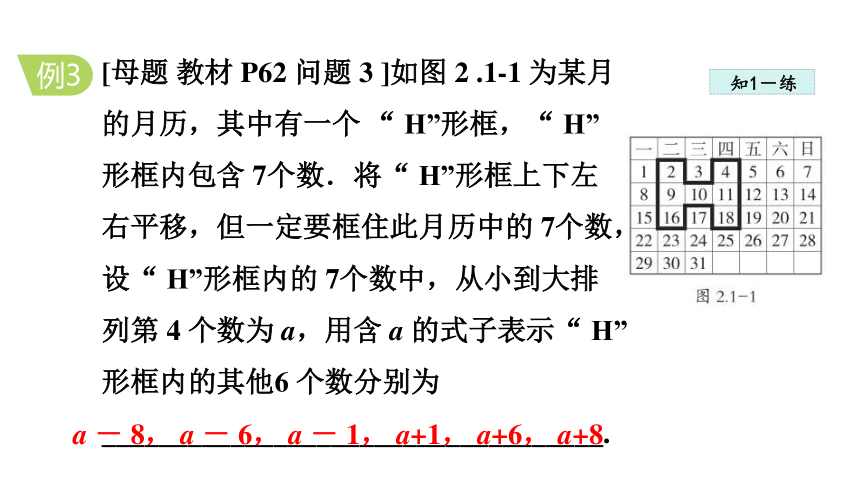
[母题 教材 P62 问题 3 ]如图 2 .1-1 为某月的月历,其中有一个 “ H”形框,“ H”形框内包含 7个数.将“ H”形框上下左右平移,但一定要框住此月历中的 7个数,设“ H”形框内的 7个数中,从小到大排列第 4 个数为 a,用含 a 的式子表示“ H”形框内的其他6 个数分别为 ___________________________________.
例3
a - 8, a - 6, a - 1, a+1, a+6, a+8
知1-练
感悟新知
解:根据图 2.1-1 可知“ H”形框内从小到大排列第 4 个数是中间的数,所以其他 6 个数分别为 a-8, a-6, a-1, a+1, a+6, a+8.
解题秘方:先找出“ H”形框中从小到大排列第 4 个数的位置,再根据其他 6 个数与这个数的差分别表示其他数即可 .
知1-练
感悟新知
3-1.如图①是某月的月历,用笔在月历中任意框出两组呈斜对角线交叉的 5 个数,如图②,若设交叉框中的五个数分别为 a, b, c, d,m,则 a, b, c, d 满足的等量关系为___________ .
a+d=b+c
感悟新知
知2-讲
知识点
代数式
2
1. 代数式的定义
用加、减、乘、除及乘方等运算符号把数或表示数的字母连接而成的式子,叫作代数式 . 单个的数或字母也是代数式 .
感悟新知
知2-讲
2. 代数式的书写规定
书写规范 举例
在代数式中如果出现乘号,通常将乘号写作“· ”或省略不写,并且数字写在字母前面 2× a 写作 2· a 或 2a, m× n 写作 m· n 或 mn
数字与数字相乘时,只能用“×”,不能省略或写成“· ” 3× 5 不能写成 35 或 3· 5
数字因数为带分数时,要化为假分数 1 × m 要写成 m
感悟新知
知2-讲
书写规范 举例
除法运算一般写成 (a ≠ 0)的形式 a÷ 2 写成 或 a
数字因数为“1”或“-1”时,常省略“1” 1× ab 写成 ab, -1× ab 写成-ab
若式子后面有单位且式子是和或差的形式,应把式子用括号括起来 ( 3a-2)岁,( a-b)千克, ( 3a+5b)元等
知2-讲
感悟新知
特别提醒
1. 在一个式子中如果含有 “=”“<”“>”“≤”“≥” 或“≠”,那么这个式子就不是代数式.
2. 单个的数或字母都可以写成它们与1 的乘积,所以它们也是代数式.
3. 代数式中可以有括号,它的作用是指明运算顺序.
感悟新知
知2-练
下列各式中哪些是代数式?哪些不是代数式?
(1) 3>2; (2) a+b=5; (3) a;
(4) 3; (5) 5+x-y; (6) 5x-3y.
例4
解题秘方:紧扣代数式的概念进行判断,特别注意单个的数和字母 .
解: (3)(4)(5)(6) 是代数式,(1)(2) 不是代数式.
知2-练
感悟新知
方法点拨:判断一个式子是否为代数式的方法:
判断一个式子是否为代数式,只需看这个式子的字母之间、数字之间或字母与数字之间是否由运算符号连接,若是,则是代数式;否则就不是代数式 .
知2-练
感悟新知
4-1.在式子 a+b,S= ab, 5, m, 8+y,m+3=2, ≤ 中, 代数式有( )
A. 6 个 B. 5 个
C. 4 个 D. 3 个
C
感悟新知
知3-讲
知识点
列代数式
3
1. 列代数式 把问题中与数量有关的语句用含数字、字母和运算符号的式子表示出来 .
感悟新知
知3-讲
2. 列代数式常用的方法如下表
方法及注意点 举例
抓关键性词语,如“大”“小” “多”“少”“和”“差”“积” “商”“倍”等,弄清题目中的量及各个量之间的关系 如“甲数的 2 倍与乙数除以 3 的商的差”中,关键性词语是“倍”“除以”“商”“差”,设甲数为 x,乙数为 y,则所列代数式为2x-
感悟新知
知3-讲
方法及注意点 举例
弄清运算顺序,通常按照“先读先写”的顺序列式 如“a 与 b 的和与 c 的积”中,“和”在“积”之前,则所列代数式为( a+b) c;而“a 与 b 的积与 c 的和”中,“积”在“和”之前,则所列代数式为 ab+c
续表
感悟新知
知3-讲
方法及注意点 举例
对于层次较多的题目,可以采取“浓缩原题,分段处理,最后组装”的方式来处理 如“x 的 3 倍与 y 的立方之和与 x 的平方与 y 的倒数之差的乘积”,此题可先浓缩为“两数和与两数差的积”,再分段处理,第一段为“3x+y3”,第二段为“x2-” ,则所列代数式为( 3x+y3) x2-
续表
感悟新知
知3-讲
方法及注意点 举例
正确运用括号,先用小括号,后用中括号,再用大括号 如“1 与 x 的差的 5 倍与 y 的差乘 3xy”,所列代数式为
3xy [5(1-x) -y]
续表
知3-讲
感悟新知
特别提醒
1. 数字因数写在字母因数的前面,排列多个字母因数时,要按字母表的顺序排列书写,如 5abc.
2. 根据实际问题列代数式时,要抓住关键性词语,弄清题中的数量关系,理清运算顺序,熟记相关公式.
感悟新知
为响应“清廉文化进校园”的政策,某校开展“清明行风、清净校风、清正教风、清新学风”系列活动,现需购买甲、乙两种清廉读本共 200 本供教职工阅读,其中甲种读本的单价为15 元,乙种读本的单价为10 元,设购买甲种读本 x 本,则购买乙种读本的费用为( )
A. 15x 元 B. 10(200-x)元
C. 15(100-x)元 D.(200-10x)元
例5
知3-练
感悟新知
解题秘方:购买乙种读本的费用=乙种读本的单价× 购买乙种读本的数量,用x表示出购买乙种读本的数量是解题的关键.
解:购买甲种读本 x 本,则购买乙种读本(200-x)本,所以购买乙种读本的费用为 10(200-x)元 .
答案:B
知3-练
感悟新知
5-1.现有甲、乙两种糖果,甲种糖果的单价是30元/千克,乙种糖果的单价是20元/千 克,将a千克甲种糖果和b千克乙种糖果混合成什锦糖果,则什锦糖果的单价为________ 元/千克(用含a和b的代数式表示).
知3-练
感悟新知
[母题 教材 P66 练习 T3 ]将形状、大小完全相同的“ ●”和线段按照一定规律摆成如图 2 .1-2 所示的图形,第1 幅图中“ ●”的个数为 3,第 2 幅图中“ ●”的个数为 8,第 3 幅图中“ ●”的个数为15,…,以此类推,则第 n 幅图中“ ●”的个数为 __________.
例6
n(n+2)
知3-练
感悟新知
解题秘方:先根据图中“ ●”的个数得出变化规律,进而求解即可 .
解:因为第 1 幅图中“ ●”的个数为 3=1× 3,
第 2 幅图中“ ●”的个数为 8=2× 4,
第 3 幅图中“ ●”的个数为 15=3× 5,
第 4 幅图中“ ●”的个数为 24=4× 6,
……所以第 n 幅图中“ ●”的个数为 n(n+2) .
知3-练
感悟新知
6-1. [模拟·宿州]如图,第1个图案中“★”有4× 1=4(个);“▲”有1+3× 1=4(个);第2个图案中“★”有4× 2=8(个); “▲”有1+3× 2=7(个);第3个图案中“★”有4× 3=12(个);“▲”有1+3× 3=10(个);… 则第n个图案中“★” 有______个,“▲”有_______个.
4n
(1+3n)
知3-练
感悟新知
[母题 教材 P65 例 3 ]每支铅笔 a 元,每本笔记本 b 元,则100-(4a+3b)(其中 100 ≥ 4a+3b)的实际意义是 ______________________________________________.
例7
用 100 元买 4 支铅笔和 3 本笔记本,还剩下的钱数
知3-练
感悟新知
解题秘方:紧扣代数式中每一部分的实际意义解题.
解:因为每支铅笔 a 元,每本笔记本 b 元,
所以 4a 表示 4 支铅笔的价格, 3b 表示 3 本笔记本的价格,所以 100-(4a+3b) 的实际意义是用 100 元买 4 支铅笔和3 本笔记本,还剩下的钱数.
知3-练
感悟新知
7-1.请你结合生活实际,对代数式“(1-8%)x”给出 一个合理解释:______________________________________________________________________________________.
每千克苹果标价为x元,商家促销,每千克优惠8%,则实际售价为每千克(1-8%)x元(答案不唯一)
知4-讲
感悟新知
知识点
单项式
4
1. 单项式 由数和字母的积组成的代数式叫作单项式 . 单个的字母或数也是单项式 .
感悟新知
2. 单项式的系数与次数
(1) 系数: 单项式中的数字因数叫作这个单项式的系数 .
(2) 次数: 一个单项式中,所有字母的指数之和叫作这个单项式的次数 .
知4-讲
感悟新知
特别提醒:
(1) 单项式的系数包括它前面的符号,且只与数字因数有关,而单项式的次数只与字母的指数有关 .
(2)确定一个单项式的次数时,要注意:①没有写指数的字母,实际上其指数是“ 1”,计算时不要将其遗漏;②不要把系数的指数当作字母的指数一同计算 . 如 52mn 4 的次数是 1+4=5, 不能把系数的指数“ 2”当作字母的指数 .
知4-讲
感悟新知
知4-讲
特别解读
1. 单项式中不含加减运算;
2.分母中含有字母的式子不是单项式,如不是单项式;
3. 指数和次数是两个不同的概念,指数是单个字母的指数,而次数是所有字母的指数之和.
知4-练
感悟新知
[母题 教材 P67 例 4 ] 找出下列各式中的单项式,并写出单项式的系数和次数 .
-m; - ; ; (a+b) h; 23xy3;π r2.
例8
分母中含有字母,不是
单项式.
知4-练
感悟新知
解:单项式有 -m, - 23xy3;π r2.
-m的系数为 - 1,次数为 1;
- 的系数为 - ,次数为 2;
23xy3的系数为 8,次数为 4;
π r2的系数为 π ,次数为 2.
1+3=4, 23 的指数 3不能加进去.
π是一个数,不是字母.
知4-练
感悟新知
8-1. [期末·亳州]下列关于单项式- 的说法中, 正确的是( )
A. 系数是- ,次数是3
B. 系数是- ,次数是2
C. 系数是- 2,次数是3
D. 系数是- 3,次数是2
A
知4-练
感悟新知
已知 2kx2yn是关于 x、 y 的一个单项式,且系数是
7,次数是 5,那么 k=______, n= ______.
3
例9
知4-练
感悟新知
解:由单项式的次数是 5,可知 x、 y 的指数和为 5,即 2+n=5,所以 n=3.
由单项式的系数是 7,可知 2k=7,所以 k=.
解题秘方:根据单项式的次数和系数的确定方法求值.
知4-练
感悟新知
9-1.若代数式(m - 2)·x|m|y是关于x, y的三次单项式,则m=_________.
-2
感悟新知
知5-讲
知识点
多项式
5
1. 多项式 几个单项式的和叫作多项式 .
一个式子是多项式需具备两个条件:
(1) 式子中含有运算符号“ +”或“-”;
(2) 分母中不含有字母 .
感悟新知
知5-讲
2. 多项式的项 在多项式中,每个单项式叫作多项式的项,其中不含字母的项叫作常数项 . 一个多项式含有几项,这个多项式就叫作几项式 .
3. 多项式的次数 一个多项式里,次数最高的项的次数叫作这个多项式的次数 .
知5-讲
感悟新知
特别提醒
1. 多项式是由单项式组成的,但不能说多项式包含单项式,它们是两个不同的概念,没有从属关系 .
2. 单项式的次数是所有字母指数的和,而多项式的次数是多项式中次数最高项的次数, 二者不能混淆.
感悟新知
知5-练
[母题 教材 P68 练习T3] 多项式a3b3 - 4ab4 - b - 的最高次项是什么?一次项系数是什么?常数项是什么?它是几次几项式?
解题秘方:利用多项式的项及次数的定义进行辨析 .
解:这个多项式的最高次项是 a3b3,一次项系数是 - 1,常数项是 - ,它是六次四项式 .
例10
知5-练
感悟新知
10-1. [期中·淮南谢家集区]多项式- x2y+3xy2+2x3y2 - 1是______次_____项式.
五
四
感悟新知
知5-练
已知关于 x 的多项式 3x4- (m+5) x3+(n-1) x2-5x+3 不含 x3项和 x2项,求 m、 n 的值 .
解题秘方:根据多项式的结构中不含某项的意义,结合相关定义,求出系数中待定字母的值 .
例11
知5-练
感悟新知
解:因为多项式
3x 4-(m+5) x 3+(n-1) x 2-5x+3 不含 x3 项和 x2 项,所以 - (m+5) =0, n-1=0,
所以 m=-5, n=1.
不含某一项,说明这
一项的系数为 0
知5-练
感悟新知
11-1.多项式 x|m|+(m - 4)x+7是关于x的四次 三 项 式,则m的 值是( )
A. 4 B. - 2
C. - 4 D. 4或- 4
C
感悟新知
知6-讲
知识点
整式
6
1. 定义 单项式与多项式统称为整式 .
感悟新知
知6-讲
2. 代数式、整式、单项式、多项式的关系 代数式包含整式,
整式又分为单项式和多项式,其包含关系如图 2.1-3.
知6-讲
感悟新知
特别解读
1. 单项式是整式 .
2.多项式是整式 .
3. 如果一个式子既不是单项式,又不是多项式,那么它一定不是整式 .
知6-练
感悟新知
将式子: 、 、 -y、π(x2-y2)、 a2、
7x-1、9a2+ -2 填入相应的大括号内:
单项式: { … };
多项式: { … };
整式: { … }.
例12
知6-练
感悟新知
解题秘方:利用单项式、多项式及整式的定义进行分类.
解: 单项式: ;
多项式: ;
整式: .
知6-练
感悟新知
方法点拨:判断一个式子是单项式还是多项式的 方法:
首先判断它是不是整式,若分母中含字母,则一定不是整式,也不可能是单项式或多项式 . 整式中含加减运算的是多项式,不含加减运算的是单项式 .
知6-练
感悟新知
12-1. [月考·六安]对下列式子进行分类.
, +3, , , .
单项式:{ …};
多项式:{ …};
整式:{ …}.
知6-练
感悟新知
知7-讲
感悟新知
知识点
代数式的值
7
1. 代数式的值 用数值代替代数式里的字母,按照代数式中字母的运算关系计算得出的结果叫作代数式的值 .
感悟新知
2. 求代数式值的步骤
(1) 代入:将指定的数值代替代数式中的字母 .
代入数值时,必须将相应的字母换成数值,其他的运算符号、数字和运算顺序都不能改变,同时对原来省略的乘号要进行还原 .
知7-讲
感悟新知
(2) 计算:按照代数式指定的运算关系计算出结果 .
代数式的值是由所含字母的取值确定的,一般随着代数式中字母取值的变化而变化,所以求代数式的值时,在代入前必须写出“当……时”,表示代数式的值是在这种情况下求得的 .
知7-讲
感悟新知
知7-讲
特别提醒
代数式中的字母取值的限制条件:
1. 不能使代数式本身失去意义,如代数式的分母中含有字母时,不能使代数式的分母为零 .
2. 不能使代数式代表的实际问题失去意义.如速度为 v 的一辆汽车在时间 t内行驶的路程为vt,这里的 v, t 只能取零或正数,而不能取负数 .
知7-练
感悟新知
[母题 教材 P69 例 6 ] 当 x= - 1, y=3 时,求下列代数式的值:
(1) x 3 - 2y; (2) | x 2 - |.
例13
解题秘方:直接将代数式中字母的值代入代数式中求值 .
知7-练
感悟新知
解:当 x=-1, y=3 时, x3-2y=(-1) 3-2× 3=-1-6=-7.
(1) x 3 - 2y
(2) | x 2 - |
当 x=-1, y=3 时,
| x2- = |(-1) 2- | = | 1- | = | | = .
知7-练
感悟新知
13-1. [月考·阜阳]若|a-3|+|b-2|=0,求a+b的值.
知7-练
感悟新知
[母题 教材 P71 练习 T2 ]如图 2.1-4,用代数式表示图中阴影部分的面积 . 当 a=2, b=1 时,阴影部分的面积是多少?
例14
知7-练
感悟新知
解题秘方:把阴影部分的面积转化成长方形面积和四分之一圆面积的差计算 .
知7-练
感悟新知
解:整个长方形的面积为 a(a+b),两个四分之一圆的面积分别为 π a2, π b 2,
故阴影部分的面积为 a(a+b) - π a2- π b 2.
当 a=2, b=1 时,阴 影 部 分 的 面 积 为 2×(2+1) - π×4- π× 1=6- π .
知7-练
感悟新知
方法点拨:求不规则图形面积的方法:
当阴影部分的图形是不规则图形时,可以采用转化思想,将不规则图形的面积转化为规则图形的面积的和(或差)来求解,解答此类试题的关键是找到阴影部分的面积与规则图形的面积之间的关系 .
知7-练
感悟新知
14-1.如图,在一个底为a,高为h的三角形铁皮上剪去一个半径为r的半圆.
(1) 用含a, h, r的代数式表示剩下铁皮
(阴影部分)的面积S;
知7-练
感悟新知
(2) 请求出当a=10, h=8,r=2时, S的值(π取3.14).
代数式
次数
系数
整式
单项式
多项式
项数
代数式
用字母
表示数
2.1 代数式
第二章 整式及其加减
学习目标
课时讲解
1
用字母表示数
代数式
列代数式
单项式
多项式
整式
代数式的值
逐点
导讲练
课堂小结
作业提升
学习目标
课时流程
2
知1-讲
感悟新知
知识点
用字母表示数
1
1. 用字母表示数 用字母或含有字母的式子表示数或数量关系 . 在用字母表示数中,字母和数一样可以参与运算,可以用式子把数量关系简明地表示出来 .
感悟新知
知1-讲
特别提醒
同一问题中,相同的字母必须表示相同的量,不同的量必须用不同的字母表示.
感悟新知
2. 用字母表示数具有如下特点
(1) 任意性:字母可以表示任意的数 .
(2) 限制性:字母的取值必须使式子有意义且符合实际情况 .
(3) 确定性:字母的取值一旦确定,式子的值也随之确定 .
(4) 一般性:用字母表示数能更准确地反映事物的规律,更具有一般性 .
知1-讲
知1-练
感悟新知
[母题 教材 P63 练习 T2] 填空:
(1)买单价为 6 元的钢笔 a 支,共需 ______元;
(2) 一台电视机的标价为 a 元,则 打 八 折 后 的 售价为______元;
例1
6a
0.8a
解题秘方:类比用具体数表示数量关系的方式,用字母表示数量关系 .
知1-练
感悟新知
1-1.[期中·北京朝阳区]一种商品每件盈利a 元,售出 60 件,共盈利_________元(用含 a的式子表示).
60a
知1-练
感悟新知
填空:
(1)三个连续偶数,若中间一个数为 2n,则其余两个数分别为 ______________;
(2)若一个两位数,其个位数字为 a,十位数字为 b,则这个两位数为 _________.
例2
2n-2, 2n+2
解题秘方:紧扣各类数的特征,用字母表示这些特征数 .
10b+a
知1-练
感悟新知
2-1.若 m 表示一个两位数, n 表示一个三位数.把 m 写在 n 的右侧组成一个五位数,则能表示这个五位数的式子是( )
A. mn
B. 100m+n
C. 100n+m
D. 1 000n+100m
C
知1-练
感悟新知
2-2.两个连续奇数中,设较大的一个数为x,那么另 一个数为( )
A. x+1 B. x+2
C. 2x+1 D. x - 2
D
知1-练
感悟新知
[母题 教材 P62 问题 3 ]如图 2 .1-1 为某月的月历,其中有一个 “ H”形框,“ H”形框内包含 7个数.将“ H”形框上下左右平移,但一定要框住此月历中的 7个数,设“ H”形框内的 7个数中,从小到大排列第 4 个数为 a,用含 a 的式子表示“ H”形框内的其他6 个数分别为 ___________________________________.
例3
a - 8, a - 6, a - 1, a+1, a+6, a+8
知1-练
感悟新知
解:根据图 2.1-1 可知“ H”形框内从小到大排列第 4 个数是中间的数,所以其他 6 个数分别为 a-8, a-6, a-1, a+1, a+6, a+8.
解题秘方:先找出“ H”形框中从小到大排列第 4 个数的位置,再根据其他 6 个数与这个数的差分别表示其他数即可 .
知1-练
感悟新知
3-1.如图①是某月的月历,用笔在月历中任意框出两组呈斜对角线交叉的 5 个数,如图②,若设交叉框中的五个数分别为 a, b, c, d,m,则 a, b, c, d 满足的等量关系为___________ .
a+d=b+c
感悟新知
知2-讲
知识点
代数式
2
1. 代数式的定义
用加、减、乘、除及乘方等运算符号把数或表示数的字母连接而成的式子,叫作代数式 . 单个的数或字母也是代数式 .
感悟新知
知2-讲
2. 代数式的书写规定
书写规范 举例
在代数式中如果出现乘号,通常将乘号写作“· ”或省略不写,并且数字写在字母前面 2× a 写作 2· a 或 2a, m× n 写作 m· n 或 mn
数字与数字相乘时,只能用“×”,不能省略或写成“· ” 3× 5 不能写成 35 或 3· 5
数字因数为带分数时,要化为假分数 1 × m 要写成 m
感悟新知
知2-讲
书写规范 举例
除法运算一般写成 (a ≠ 0)的形式 a÷ 2 写成 或 a
数字因数为“1”或“-1”时,常省略“1” 1× ab 写成 ab, -1× ab 写成-ab
若式子后面有单位且式子是和或差的形式,应把式子用括号括起来 ( 3a-2)岁,( a-b)千克, ( 3a+5b)元等
知2-讲
感悟新知
特别提醒
1. 在一个式子中如果含有 “=”“<”“>”“≤”“≥” 或“≠”,那么这个式子就不是代数式.
2. 单个的数或字母都可以写成它们与1 的乘积,所以它们也是代数式.
3. 代数式中可以有括号,它的作用是指明运算顺序.
感悟新知
知2-练
下列各式中哪些是代数式?哪些不是代数式?
(1) 3>2; (2) a+b=5; (3) a;
(4) 3; (5) 5+x-y; (6) 5x-3y.
例4
解题秘方:紧扣代数式的概念进行判断,特别注意单个的数和字母 .
解: (3)(4)(5)(6) 是代数式,(1)(2) 不是代数式.
知2-练
感悟新知
方法点拨:判断一个式子是否为代数式的方法:
判断一个式子是否为代数式,只需看这个式子的字母之间、数字之间或字母与数字之间是否由运算符号连接,若是,则是代数式;否则就不是代数式 .
知2-练
感悟新知
4-1.在式子 a+b,S= ab, 5, m, 8+y,m+3=2, ≤ 中, 代数式有( )
A. 6 个 B. 5 个
C. 4 个 D. 3 个
C
感悟新知
知3-讲
知识点
列代数式
3
1. 列代数式 把问题中与数量有关的语句用含数字、字母和运算符号的式子表示出来 .
感悟新知
知3-讲
2. 列代数式常用的方法如下表
方法及注意点 举例
抓关键性词语,如“大”“小” “多”“少”“和”“差”“积” “商”“倍”等,弄清题目中的量及各个量之间的关系 如“甲数的 2 倍与乙数除以 3 的商的差”中,关键性词语是“倍”“除以”“商”“差”,设甲数为 x,乙数为 y,则所列代数式为2x-
感悟新知
知3-讲
方法及注意点 举例
弄清运算顺序,通常按照“先读先写”的顺序列式 如“a 与 b 的和与 c 的积”中,“和”在“积”之前,则所列代数式为( a+b) c;而“a 与 b 的积与 c 的和”中,“积”在“和”之前,则所列代数式为 ab+c
续表
感悟新知
知3-讲
方法及注意点 举例
对于层次较多的题目,可以采取“浓缩原题,分段处理,最后组装”的方式来处理 如“x 的 3 倍与 y 的立方之和与 x 的平方与 y 的倒数之差的乘积”,此题可先浓缩为“两数和与两数差的积”,再分段处理,第一段为“3x+y3”,第二段为“x2-” ,则所列代数式为( 3x+y3) x2-
续表
感悟新知
知3-讲
方法及注意点 举例
正确运用括号,先用小括号,后用中括号,再用大括号 如“1 与 x 的差的 5 倍与 y 的差乘 3xy”,所列代数式为
3xy [5(1-x) -y]
续表
知3-讲
感悟新知
特别提醒
1. 数字因数写在字母因数的前面,排列多个字母因数时,要按字母表的顺序排列书写,如 5abc.
2. 根据实际问题列代数式时,要抓住关键性词语,弄清题中的数量关系,理清运算顺序,熟记相关公式.
感悟新知
为响应“清廉文化进校园”的政策,某校开展“清明行风、清净校风、清正教风、清新学风”系列活动,现需购买甲、乙两种清廉读本共 200 本供教职工阅读,其中甲种读本的单价为15 元,乙种读本的单价为10 元,设购买甲种读本 x 本,则购买乙种读本的费用为( )
A. 15x 元 B. 10(200-x)元
C. 15(100-x)元 D.(200-10x)元
例5
知3-练
感悟新知
解题秘方:购买乙种读本的费用=乙种读本的单价× 购买乙种读本的数量,用x表示出购买乙种读本的数量是解题的关键.
解:购买甲种读本 x 本,则购买乙种读本(200-x)本,所以购买乙种读本的费用为 10(200-x)元 .
答案:B
知3-练
感悟新知
5-1.现有甲、乙两种糖果,甲种糖果的单价是30元/千克,乙种糖果的单价是20元/千 克,将a千克甲种糖果和b千克乙种糖果混合成什锦糖果,则什锦糖果的单价为________ 元/千克(用含a和b的代数式表示).
知3-练
感悟新知
[母题 教材 P66 练习 T3 ]将形状、大小完全相同的“ ●”和线段按照一定规律摆成如图 2 .1-2 所示的图形,第1 幅图中“ ●”的个数为 3,第 2 幅图中“ ●”的个数为 8,第 3 幅图中“ ●”的个数为15,…,以此类推,则第 n 幅图中“ ●”的个数为 __________.
例6
n(n+2)
知3-练
感悟新知
解题秘方:先根据图中“ ●”的个数得出变化规律,进而求解即可 .
解:因为第 1 幅图中“ ●”的个数为 3=1× 3,
第 2 幅图中“ ●”的个数为 8=2× 4,
第 3 幅图中“ ●”的个数为 15=3× 5,
第 4 幅图中“ ●”的个数为 24=4× 6,
……所以第 n 幅图中“ ●”的个数为 n(n+2) .
知3-练
感悟新知
6-1. [模拟·宿州]如图,第1个图案中“★”有4× 1=4(个);“▲”有1+3× 1=4(个);第2个图案中“★”有4× 2=8(个); “▲”有1+3× 2=7(个);第3个图案中“★”有4× 3=12(个);“▲”有1+3× 3=10(个);… 则第n个图案中“★” 有______个,“▲”有_______个.
4n
(1+3n)
知3-练
感悟新知
[母题 教材 P65 例 3 ]每支铅笔 a 元,每本笔记本 b 元,则100-(4a+3b)(其中 100 ≥ 4a+3b)的实际意义是 ______________________________________________.
例7
用 100 元买 4 支铅笔和 3 本笔记本,还剩下的钱数
知3-练
感悟新知
解题秘方:紧扣代数式中每一部分的实际意义解题.
解:因为每支铅笔 a 元,每本笔记本 b 元,
所以 4a 表示 4 支铅笔的价格, 3b 表示 3 本笔记本的价格,所以 100-(4a+3b) 的实际意义是用 100 元买 4 支铅笔和3 本笔记本,还剩下的钱数.
知3-练
感悟新知
7-1.请你结合生活实际,对代数式“(1-8%)x”给出 一个合理解释:______________________________________________________________________________________.
每千克苹果标价为x元,商家促销,每千克优惠8%,则实际售价为每千克(1-8%)x元(答案不唯一)
知4-讲
感悟新知
知识点
单项式
4
1. 单项式 由数和字母的积组成的代数式叫作单项式 . 单个的字母或数也是单项式 .
感悟新知
2. 单项式的系数与次数
(1) 系数: 单项式中的数字因数叫作这个单项式的系数 .
(2) 次数: 一个单项式中,所有字母的指数之和叫作这个单项式的次数 .
知4-讲
感悟新知
特别提醒:
(1) 单项式的系数包括它前面的符号,且只与数字因数有关,而单项式的次数只与字母的指数有关 .
(2)确定一个单项式的次数时,要注意:①没有写指数的字母,实际上其指数是“ 1”,计算时不要将其遗漏;②不要把系数的指数当作字母的指数一同计算 . 如 52mn 4 的次数是 1+4=5, 不能把系数的指数“ 2”当作字母的指数 .
知4-讲
感悟新知
知4-讲
特别解读
1. 单项式中不含加减运算;
2.分母中含有字母的式子不是单项式,如不是单项式;
3. 指数和次数是两个不同的概念,指数是单个字母的指数,而次数是所有字母的指数之和.
知4-练
感悟新知
[母题 教材 P67 例 4 ] 找出下列各式中的单项式,并写出单项式的系数和次数 .
-m; - ; ; (a+b) h; 23xy3;π r2.
例8
分母中含有字母,不是
单项式.
知4-练
感悟新知
解:单项式有 -m, - 23xy3;π r2.
-m的系数为 - 1,次数为 1;
- 的系数为 - ,次数为 2;
23xy3的系数为 8,次数为 4;
π r2的系数为 π ,次数为 2.
1+3=4, 23 的指数 3不能加进去.
π是一个数,不是字母.
知4-练
感悟新知
8-1. [期末·亳州]下列关于单项式- 的说法中, 正确的是( )
A. 系数是- ,次数是3
B. 系数是- ,次数是2
C. 系数是- 2,次数是3
D. 系数是- 3,次数是2
A
知4-练
感悟新知
已知 2kx2yn是关于 x、 y 的一个单项式,且系数是
7,次数是 5,那么 k=______, n= ______.
3
例9
知4-练
感悟新知
解:由单项式的次数是 5,可知 x、 y 的指数和为 5,即 2+n=5,所以 n=3.
由单项式的系数是 7,可知 2k=7,所以 k=.
解题秘方:根据单项式的次数和系数的确定方法求值.
知4-练
感悟新知
9-1.若代数式(m - 2)·x|m|y是关于x, y的三次单项式,则m=_________.
-2
感悟新知
知5-讲
知识点
多项式
5
1. 多项式 几个单项式的和叫作多项式 .
一个式子是多项式需具备两个条件:
(1) 式子中含有运算符号“ +”或“-”;
(2) 分母中不含有字母 .
感悟新知
知5-讲
2. 多项式的项 在多项式中,每个单项式叫作多项式的项,其中不含字母的项叫作常数项 . 一个多项式含有几项,这个多项式就叫作几项式 .
3. 多项式的次数 一个多项式里,次数最高的项的次数叫作这个多项式的次数 .
知5-讲
感悟新知
特别提醒
1. 多项式是由单项式组成的,但不能说多项式包含单项式,它们是两个不同的概念,没有从属关系 .
2. 单项式的次数是所有字母指数的和,而多项式的次数是多项式中次数最高项的次数, 二者不能混淆.
感悟新知
知5-练
[母题 教材 P68 练习T3] 多项式a3b3 - 4ab4 - b - 的最高次项是什么?一次项系数是什么?常数项是什么?它是几次几项式?
解题秘方:利用多项式的项及次数的定义进行辨析 .
解:这个多项式的最高次项是 a3b3,一次项系数是 - 1,常数项是 - ,它是六次四项式 .
例10
知5-练
感悟新知
10-1. [期中·淮南谢家集区]多项式- x2y+3xy2+2x3y2 - 1是______次_____项式.
五
四
感悟新知
知5-练
已知关于 x 的多项式 3x4- (m+5) x3+(n-1) x2-5x+3 不含 x3项和 x2项,求 m、 n 的值 .
解题秘方:根据多项式的结构中不含某项的意义,结合相关定义,求出系数中待定字母的值 .
例11
知5-练
感悟新知
解:因为多项式
3x 4-(m+5) x 3+(n-1) x 2-5x+3 不含 x3 项和 x2 项,所以 - (m+5) =0, n-1=0,
所以 m=-5, n=1.
不含某一项,说明这
一项的系数为 0
知5-练
感悟新知
11-1.多项式 x|m|+(m - 4)x+7是关于x的四次 三 项 式,则m的 值是( )
A. 4 B. - 2
C. - 4 D. 4或- 4
C
感悟新知
知6-讲
知识点
整式
6
1. 定义 单项式与多项式统称为整式 .
感悟新知
知6-讲
2. 代数式、整式、单项式、多项式的关系 代数式包含整式,
整式又分为单项式和多项式,其包含关系如图 2.1-3.
知6-讲
感悟新知
特别解读
1. 单项式是整式 .
2.多项式是整式 .
3. 如果一个式子既不是单项式,又不是多项式,那么它一定不是整式 .
知6-练
感悟新知
将式子: 、 、 -y、π(x2-y2)、 a2、
7x-1、9a2+ -2 填入相应的大括号内:
单项式: { … };
多项式: { … };
整式: { … }.
例12
知6-练
感悟新知
解题秘方:利用单项式、多项式及整式的定义进行分类.
解: 单项式: ;
多项式: ;
整式: .
知6-练
感悟新知
方法点拨:判断一个式子是单项式还是多项式的 方法:
首先判断它是不是整式,若分母中含字母,则一定不是整式,也不可能是单项式或多项式 . 整式中含加减运算的是多项式,不含加减运算的是单项式 .
知6-练
感悟新知
12-1. [月考·六安]对下列式子进行分类.
, +3, , , .
单项式:{ …};
多项式:{ …};
整式:{ …}.
知6-练
感悟新知
知7-讲
感悟新知
知识点
代数式的值
7
1. 代数式的值 用数值代替代数式里的字母,按照代数式中字母的运算关系计算得出的结果叫作代数式的值 .
感悟新知
2. 求代数式值的步骤
(1) 代入:将指定的数值代替代数式中的字母 .
代入数值时,必须将相应的字母换成数值,其他的运算符号、数字和运算顺序都不能改变,同时对原来省略的乘号要进行还原 .
知7-讲
感悟新知
(2) 计算:按照代数式指定的运算关系计算出结果 .
代数式的值是由所含字母的取值确定的,一般随着代数式中字母取值的变化而变化,所以求代数式的值时,在代入前必须写出“当……时”,表示代数式的值是在这种情况下求得的 .
知7-讲
感悟新知
知7-讲
特别提醒
代数式中的字母取值的限制条件:
1. 不能使代数式本身失去意义,如代数式的分母中含有字母时,不能使代数式的分母为零 .
2. 不能使代数式代表的实际问题失去意义.如速度为 v 的一辆汽车在时间 t内行驶的路程为vt,这里的 v, t 只能取零或正数,而不能取负数 .
知7-练
感悟新知
[母题 教材 P69 例 6 ] 当 x= - 1, y=3 时,求下列代数式的值:
(1) x 3 - 2y; (2) | x 2 - |.
例13
解题秘方:直接将代数式中字母的值代入代数式中求值 .
知7-练
感悟新知
解:当 x=-1, y=3 时, x3-2y=(-1) 3-2× 3=-1-6=-7.
(1) x 3 - 2y
(2) | x 2 - |
当 x=-1, y=3 时,
| x2- = |(-1) 2- | = | 1- | = | | = .
知7-练
感悟新知
13-1. [月考·阜阳]若|a-3|+|b-2|=0,求a+b的值.
知7-练
感悟新知
[母题 教材 P71 练习 T2 ]如图 2.1-4,用代数式表示图中阴影部分的面积 . 当 a=2, b=1 时,阴影部分的面积是多少?
例14
知7-练
感悟新知
解题秘方:把阴影部分的面积转化成长方形面积和四分之一圆面积的差计算 .
知7-练
感悟新知
解:整个长方形的面积为 a(a+b),两个四分之一圆的面积分别为 π a2, π b 2,
故阴影部分的面积为 a(a+b) - π a2- π b 2.
当 a=2, b=1 时,阴 影 部 分 的 面 积 为 2×(2+1) - π×4- π× 1=6- π .
知7-练
感悟新知
方法点拨:求不规则图形面积的方法:
当阴影部分的图形是不规则图形时,可以采用转化思想,将不规则图形的面积转化为规则图形的面积的和(或差)来求解,解答此类试题的关键是找到阴影部分的面积与规则图形的面积之间的关系 .
知7-练
感悟新知
14-1.如图,在一个底为a,高为h的三角形铁皮上剪去一个半径为r的半圆.
(1) 用含a, h, r的代数式表示剩下铁皮
(阴影部分)的面积S;
知7-练
感悟新知
(2) 请求出当a=10, h=8,r=2时, S的值(π取3.14).
代数式
次数
系数
整式
单项式
多项式
项数
代数式
用字母
表示数
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
