2023-2024学年浙江省丽水市莲都区七年级(上)期末数学试卷(含答案)
文档属性
| 名称 | 2023-2024学年浙江省丽水市莲都区七年级(上)期末数学试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 334.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-12 16:14:11 | ||
图片预览



文档简介
2023-2024学年浙江省丽水市莲都区七年级(上)期末数学试卷
一、选择题(本题有10小题,每小题3分,共30分.)
1.(3分)实数﹣3的相反数是( )
A.﹣ B. C.3 D.﹣3
2.(3分)文化和旅游部数据显示,2023年的中秋、国庆假期全国国内旅游出游人数8.26亿人次,实现国内旅游收入7534.3亿元.数据8.26亿用科学记数法表示为( )
A.8.26×109 B.82.6×108 C.8.26×108 D.82.6×107
3.(3分)下列实数中,属于无理数的是( )
A.3.14 B. C. D.π
4.(3分)多项式x2y﹣xy﹣1的次数和常数项分别是( )
A.3,1 B.3,﹣1 C.5,1 D.5,﹣1
5.(3分)下列方程变形过程正确的是( )
A.由x+3=6,得x=6+3 B.由5x=3,得
C.由x+5=1,得x=5﹣1 D.由,得x=0
6.(3分)如图,AB⊥BC,DB⊥AC,下列线段的长能表示点B到AC的距离的是( )
A.AB B.BD C.BC D.AD
7.(3分)用代数式表示“a与b的平方的差”正确的是( )
A.a2﹣b2 B.(a﹣b)2 C.a﹣b2 D.a2﹣b
8.(3分)下列四个式子中,计算结果最小的是( )
A.(﹣3﹣2)2 B.(﹣3)×(﹣2)2
C.﹣32÷(﹣2)2 D.﹣32﹣23
9.(3分)2023年杭州亚运会上,我国获得奖牌383枚,其中银牌111枚,金牌数是铜牌数的3倍少12枚.若设金牌数是x,则可列出方程为( )
A.(3x﹣12)+x=383﹣111 B.3(x+12)+x=383﹣111
C. D.
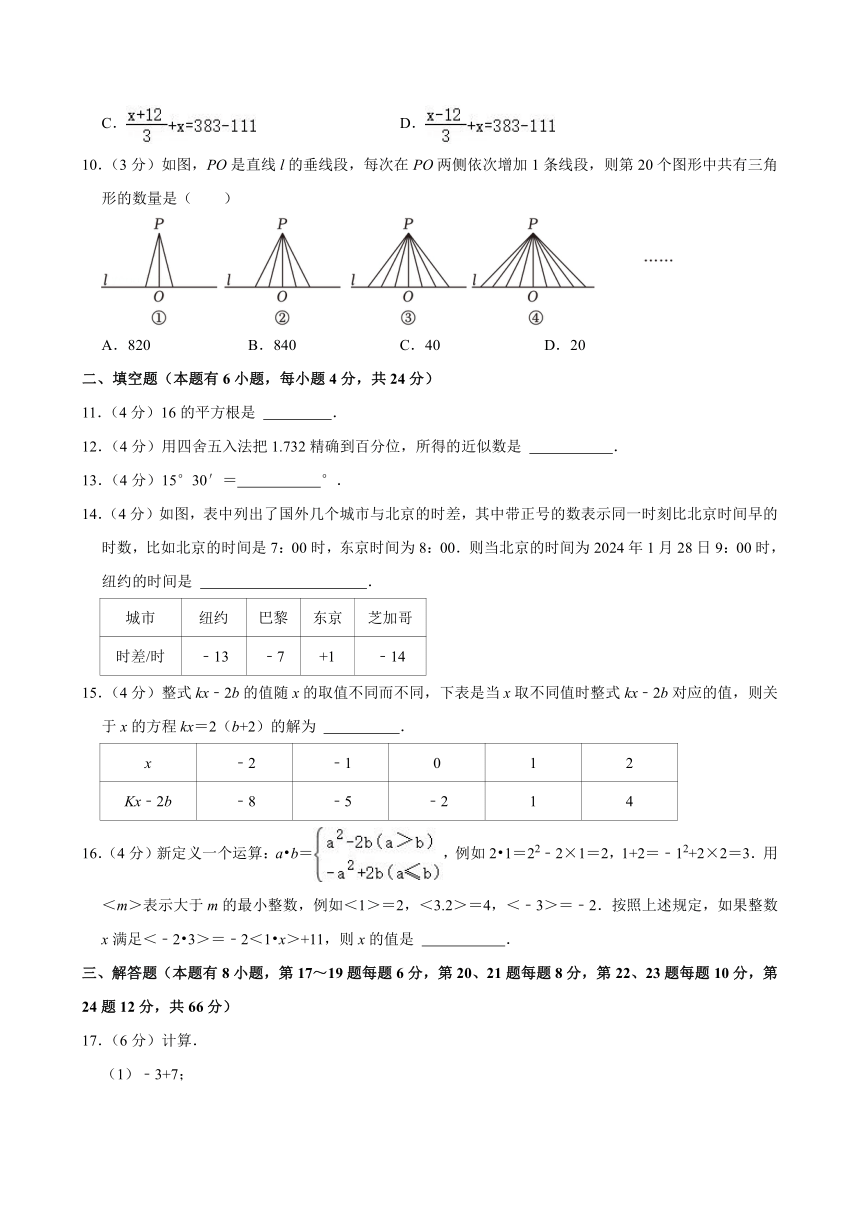
10.(3分)如图,PO是直线l的垂线段,每次在PO两侧依次增加1条线段,则第20个图形中共有三角形的数量是( )
A.820 B.840 C.40 D.20
二、填空题(本题有6小题,每小题4分,共24分)
11.(4分)16的平方根是 .
12.(4分)用四舍五入法把1.732精确到百分位,所得的近似数是 .
13.(4分)15°30′= °.
14.(4分)如图,表中列出了国外几个城市与北京的时差,其中带正号的数表示同一时刻比北京时间早的时数,比如北京的时间是7:00时,东京时间为8:00.则当北京的时间为2024年1月28日9:00时,纽约的时间是 .
城市 纽约 巴黎 东京 芝加哥
时差/时 ﹣13 ﹣7 +1 ﹣14
15.(4分)整式kx﹣2b的值随x的取值不同而不同,下表是当x取不同值时整式kx﹣2b对应的值,则关于x的方程kx=2(b+2)的解为 .
x ﹣2 ﹣1 0 1 2
Kx﹣2b ﹣8 ﹣5 ﹣2 1 4
16.(4分)新定义一个运算:a b=,例如2 1=22﹣2×1=2,1+2=﹣12+2×2=3.用<m>表示大于m的最小整数,例如<1>=2,<3.2>=4,<﹣3>=﹣2.按照上述规定,如果整数x满足<﹣2 3>=﹣2<1 x>+11,则x的值是 .
三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
17.(6分)计算.
(1)﹣3+7;
(2).
18.(6分)解方程.
(1)3x=10﹣2x;
(2).
19.(6分)先化简,再求值:,其中x=2,y=﹣3.
20.(8分)如图,已知线段AB和点C,请用直尺和圆规作图(不要求写出作图过程,要保留作图痕迹).
(1)作射线CA、直线CB;
(2)比较大小:AC+AB CB,依据: ;
(3)在射线BC上取一点D,使CD=2AB.
21.(8分)如图,点O是直线AB上的一点,射线OC,OD在直线AB的异侧,已知OC⊥OD,OE平分∠AOC.
(1)若∠BOD=40°,求∠AOE的度数;
(2)∠AOE与∠BOD是否有可能成为对顶角?若有可能,请求出∠BOD的度数;若不可能,请说明理由.
22.(10分)如图1是1个纸杯和6个叠放在一起的纸杯的示意图,量得1个纸杯的高为10cm,6个叠放在一起的纸杯的高为14cm.
(1)问2个叠放在一起的纸杯的高是多少cm?
(2)若一批这样的纸杯按照图2的方式叠放,测得总高度为90cm,求纸杯个数.
23.(10分)在数轴上点A,B,C所表示的数分别是﹣2,6,x(x>﹣2).
(1)求AB的长;
(2)若点D是AB的中点,用含x的代数式表示CD的长;
(3)若点A以每秒5个单位的速度向左运动,同时,点B以每秒20个单位的速度向右运动,点C从原点开始以每秒1个单位的速度向右运动,记OB的中点为E,AC的中点为F,试通过计算说明的结果是定值.
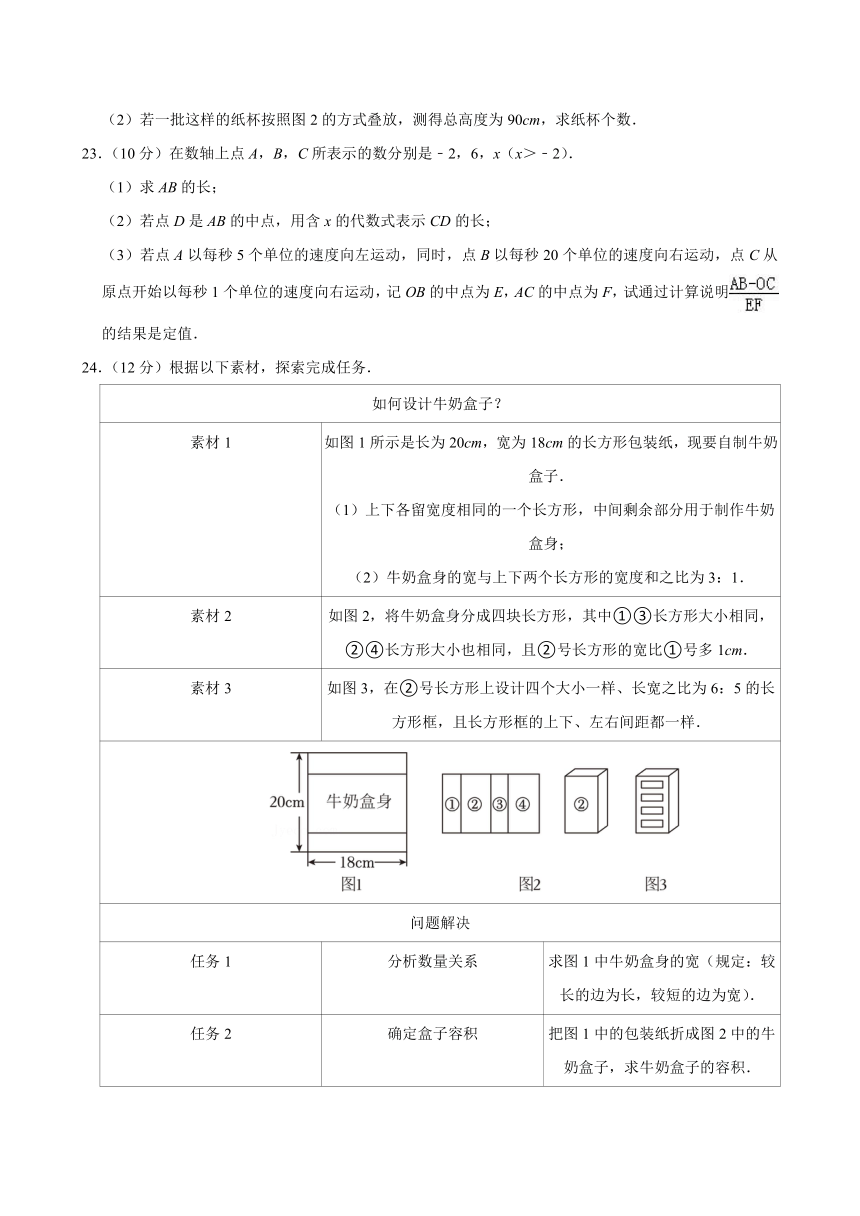
24.(12分)根据以下素材,探索完成任务.
如何设计牛奶盒子?
素材1 如图1所示是长为20cm,宽为18cm的长方形包装纸,现要自制牛奶盒子.(1)上下各留宽度相同的一个长方形,中间剩余部分用于制作牛奶盒身;(2)牛奶盒身的宽与上下两个长方形的宽度和之比为3:1.
素材2 如图2,将牛奶盒身分成四块长方形,其中①③长方形大小相同,②④长方形大小也相同,且②号长方形的宽比①号多1cm.
素材3 如图3,在②号长方形上设计四个大小一样、长宽之比为6:5的长方形框,且长方形框的上下、左右间距都一样.
问题解决
任务1 分析数量关系 求图1中牛奶盒身的宽(规定:较长的边为长,较短的边为宽).
任务2 确定盒子容积 把图1中的包装纸折成图2中的牛奶盒子,求牛奶盒子的容积.
任务3 确定间距大小 求出图3中②号长方形上设计的长方形框之间的间距.
2023-2024学年浙江省丽水市莲都区七年级(上)期末数学试卷
参考答案
一、选择题(本题有10小题,每小题3分,共30分.)
1.(3分)实数﹣3的相反数是( )
A.﹣ B. C.3 D.﹣3
选:C.
2.(3分)文化和旅游部数据显示,2023年的中秋、国庆假期全国国内旅游出游人数8.26亿人次,实现国内旅游收入7534.3亿元.数据8.26亿用科学记数法表示为( )
A.8.26×109 B.82.6×108 C.8.26×108 D.82.6×107
选:C.
3.(3分)下列实数中,属于无理数的是( )
A.3.14 B. C. D.π
选:D.
4.(3分)多项式x2y﹣xy﹣1的次数和常数项分别是( )
A.3,1 B.3,﹣1 C.5,1 D.5,﹣1
选:B.
5.(3分)下列方程变形过程正确的是( )
A.由x+3=6,得x=6+3 B.由5x=3,得
C.由x+5=1,得x=5﹣1 D.由,得x=0
选:D.
6.(3分)如图,AB⊥BC,DB⊥AC,下列线段的长能表示点B到AC的距离的是( )
A.AB B.BD C.BC D.AD
选:B.
7.(3分)用代数式表示“a与b的平方的差”正确的是( )
A.a2﹣b2 B.(a﹣b)2 C.a﹣b2 D.a2﹣b
选:A.
8.(3分)下列四个式子中,计算结果最小的是( )
A.(﹣3﹣2)2 B.(﹣3)×(﹣2)2
C.﹣32÷(﹣2)2 D.﹣32﹣23
选:D.
9.(3分)2023年杭州亚运会上,我国获得奖牌383枚,其中银牌111枚,金牌数是铜牌数的3倍少12枚.若设金牌数是x,则可列出方程为( )
A.(3x﹣12)+x=383﹣111 B.3(x+12)+x=383﹣111
C. D.
选:C.
10.(3分)如图,PO是直线l的垂线段,每次在PO两侧依次增加1条线段,则第20个图形中共有三角形的数量是( )
A.820 B.840 C.40 D.20
选:A.
二、填空题(本题有6小题,每小题4分,共24分)
11.(4分)16的平方根是 ±4 .
12.(4分)用四舍五入法把1.732精确到百分位,所得的近似数是 1.73 .
13.(4分)15°30′= 15.5 °.
14.(4分)如图,表中列出了国外几个城市与北京的时差,其中带正号的数表示同一时刻比北京时间早的时数,比如北京的时间是7:00时,东京时间为8:00.则当北京的时间为2024年1月28日9:00时,纽约的时间是 2024年1月27日20:00时 .
城市 纽约 巴黎 东京 芝加哥
时差/时 ﹣13 ﹣7 +1 ﹣14
15.(4分)整式kx﹣2b的值随x的取值不同而不同,下表是当x取不同值时整式kx﹣2b对应的值,则关于x的方程kx=2(b+2)的解为 x=2 .
x ﹣2 ﹣1 0 1 2
Kx﹣2b ﹣8 ﹣5 ﹣2 1 4
16.(4分)新定义一个运算:a b=,例如2 1=22﹣2×1=2,1+2=﹣12+2×2=3.用<m>表示大于m的最小整数,例如<1>=2,<3.2>=4,<﹣3>=﹣2.按照上述规定,如果整数x满足<﹣2 3>=﹣2<1 x>+11,则x的值是 ﹣1或2 .
三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
17.(6分)计算.
(1)﹣3+7;
(2).
【解答】解:(1)原式=4;
(2)原式=﹣1+2×3+2
=﹣1+6+2
=7.
18.(6分)解方程.
(1)3x=10﹣2x;
(2).
【解答】解:(1)移项,得3x+2x=10,
合并同类项,得5x=10,
两边同除以5,得x=2.
(2)去分母,得2(3x﹣1)=12﹣(4x﹣1),
去括号,得6x﹣2=12﹣4x+1,
移项,得6x+4x=12+1+2,
合并同类项,得10x=15,
两边同除以10,得x=.
19.(6分)先化简,再求值:,其中x=2,y=﹣3.
【解答】解:原式=3x2﹣6xy﹣x2+5xy
=2x2﹣xy;
当x=2,y=﹣3时,
原式=2×22﹣2×(﹣3)=8+6=14.
20.(8分)如图,已知线段AB和点C,请用直尺和圆规作图(不要求写出作图过程,要保留作图痕迹).
(1)作射线CA、直线CB;
(2)比较大小:AC+AB > CB,依据: 两点之间线段最短 ;
(3)在射线BC上取一点D,使CD=2AB.
【解答】解:(1)如图,射线CA,直线BC即为所求;
(2)AC+AB>BC(两点之间线段最短).
故答案为:>,两点之间线段最短;
(3)如图,点D即为所求.
21.(8分)如图,点O是直线AB上的一点,射线OC,OD在直线AB的异侧,已知OC⊥OD,OE平分∠AOC.
(1)若∠BOD=40°,求∠AOE的度数;
(2)∠AOE与∠BOD是否有可能成为对顶角?若有可能,请求出∠BOD的度数;若不可能,请说明理由.
【解答】解:(1)∵OC⊥OD,
∴∠BOC+∠BOD=90°,
∴∠BOC=90°﹣∠BOD=50°,
∴∠AOC=180°﹣∠BOC=130°,
∵OE平分∠AOC,
∴∠AOE=∠AOC=65°;
(2)∠AOE与∠BOD是不可能成为对顶角,理由如下:
当∠AOE=∠BOD时,∠BOD+∠BOC+∠COE=180°,
∵OE平分∠AOC,
∴∠AOE=∠COE,
∴∠BOD=∠COE,
∵OC⊥OD,
∴∠BOC+∠BOD=90°,
∴∠BOC+∠COE=90°,
∴∠BOC+∠BOD+∠BOC+∠COE=180°,
与∠BOD+∠BOC+∠COE=180°相矛盾,
∴∠AOE与∠BOD是不可能成为对顶角.
22.(10分)如图1是1个纸杯和6个叠放在一起的纸杯的示意图,量得1个纸杯的高为10cm,6个叠放在一起的纸杯的高为14cm.
(1)问2个叠放在一起的纸杯的高是多少cm?
(2)若一批这样的纸杯按照图2的方式叠放,测得总高度为90cm,求纸杯个数.
【解答】解:(1)根据题意得:
10+(14﹣10)÷5
=10+4÷5
=10.8(cm),
则2个叠放在一起的纸杯的高是10.8cm;
(2)根据题意得:
(90﹣10)÷0.8+1
=80÷0.8+1
=101(个),
则纸杯个数为101个.
23.(10分)在数轴上点A,B,C所表示的数分别是﹣2,6,x(x>﹣2).
(1)求AB的长;
(2)若点D是AB的中点,用含x的代数式表示CD的长;
(3)若点A以每秒5个单位的速度向左运动,同时,点B以每秒20个单位的速度向右运动,点C从原点开始以每秒1个单位的速度向右运动,记OB的中点为E,AC的中点为F,试通过计算说明的结果是定值.
【解答】解:(1)因为点A,B所表示的数分别是﹣2,6,
所以AB=6﹣(﹣2)=8.
(2)因为点D是AB的中点,
所以,
则点D表示的数是2.
当﹣2<x≤2时,
CD=2﹣x.
当x>2时,
CD=x﹣2.
(3)设运动的时间为t,
则点C运动后对应点所表示的数为t,点A运动后对应点所表示的数为﹣2﹣5t,点B运动后对应点所表示的数为6+20t,
因为OB的中点为E,
所以点E所表示的数为3+10t.
因为AC中点为F,
所以点F所表示的数为﹣1﹣2t,
所以AB=6+20t﹣(﹣2﹣5t)=8+25t,OC=t,EF=4+12t,
所以=.
24.(12分)根据以下素材,探索完成任务.
如何设计牛奶盒子?
素材1 如图1所示是长为20cm,宽为18cm的长方形包装纸,现要自制牛奶盒子.(1)上下各留宽度相同的一个长方形,中间剩余部分用于制作牛奶盒身;(2)牛奶盒身的宽与上下两个长方形的宽度和之比为3:1.
素材2 如图2,将牛奶盒身分成四块长方形,其中①③长方形大小相同,②④长方形大小也相同,且②号长方形的宽比①号多1cm.
素材3 如图3,在②号长方形上设计四个大小一样、长宽之比为6:5的长方形框,且长方形框的上下、左右间距都一样.
问题解决
任务1 分析数量关系 求图1中牛奶盒身的宽(规定:较长的边为长,较短的边为宽).
任务2 确定盒子容积 把图1中的包装纸折成图2中的牛奶盒子,求牛奶盒子的容积.
任务3 确定间距大小 求出图3中②号长方形上设计的长方形框之间的间距.
【解答】解:任务一:20÷(3+1)×3=15(cm),
15cm<18cm,
答:牛奶盒身的宽是15cm.
任务二:(18﹣2)÷4=4(cm),
4+1=5(cm),
V=15×4×5=300(cm3),
答:牛奶盒子的容积是300cm3,
任务三:设长方形框长为6x cm,宽为5x cm,
(5﹣6x)÷2=(15﹣4×5x)÷5
解得:x=0.5,
(5﹣6×0.5)÷2=1(cm),
答:长方形框之间的间距为1cm.
一、选择题(本题有10小题,每小题3分,共30分.)
1.(3分)实数﹣3的相反数是( )
A.﹣ B. C.3 D.﹣3
2.(3分)文化和旅游部数据显示,2023年的中秋、国庆假期全国国内旅游出游人数8.26亿人次,实现国内旅游收入7534.3亿元.数据8.26亿用科学记数法表示为( )
A.8.26×109 B.82.6×108 C.8.26×108 D.82.6×107
3.(3分)下列实数中,属于无理数的是( )
A.3.14 B. C. D.π
4.(3分)多项式x2y﹣xy﹣1的次数和常数项分别是( )
A.3,1 B.3,﹣1 C.5,1 D.5,﹣1
5.(3分)下列方程变形过程正确的是( )
A.由x+3=6,得x=6+3 B.由5x=3,得
C.由x+5=1,得x=5﹣1 D.由,得x=0
6.(3分)如图,AB⊥BC,DB⊥AC,下列线段的长能表示点B到AC的距离的是( )
A.AB B.BD C.BC D.AD
7.(3分)用代数式表示“a与b的平方的差”正确的是( )
A.a2﹣b2 B.(a﹣b)2 C.a﹣b2 D.a2﹣b
8.(3分)下列四个式子中,计算结果最小的是( )
A.(﹣3﹣2)2 B.(﹣3)×(﹣2)2
C.﹣32÷(﹣2)2 D.﹣32﹣23
9.(3分)2023年杭州亚运会上,我国获得奖牌383枚,其中银牌111枚,金牌数是铜牌数的3倍少12枚.若设金牌数是x,则可列出方程为( )
A.(3x﹣12)+x=383﹣111 B.3(x+12)+x=383﹣111
C. D.
10.(3分)如图,PO是直线l的垂线段,每次在PO两侧依次增加1条线段,则第20个图形中共有三角形的数量是( )
A.820 B.840 C.40 D.20
二、填空题(本题有6小题,每小题4分,共24分)
11.(4分)16的平方根是 .
12.(4分)用四舍五入法把1.732精确到百分位,所得的近似数是 .
13.(4分)15°30′= °.
14.(4分)如图,表中列出了国外几个城市与北京的时差,其中带正号的数表示同一时刻比北京时间早的时数,比如北京的时间是7:00时,东京时间为8:00.则当北京的时间为2024年1月28日9:00时,纽约的时间是 .
城市 纽约 巴黎 东京 芝加哥
时差/时 ﹣13 ﹣7 +1 ﹣14
15.(4分)整式kx﹣2b的值随x的取值不同而不同,下表是当x取不同值时整式kx﹣2b对应的值,则关于x的方程kx=2(b+2)的解为 .
x ﹣2 ﹣1 0 1 2
Kx﹣2b ﹣8 ﹣5 ﹣2 1 4
16.(4分)新定义一个运算:a b=,例如2 1=22﹣2×1=2,1+2=﹣12+2×2=3.用<m>表示大于m的最小整数,例如<1>=2,<3.2>=4,<﹣3>=﹣2.按照上述规定,如果整数x满足<﹣2 3>=﹣2<1 x>+11,则x的值是 .
三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
17.(6分)计算.
(1)﹣3+7;
(2).
18.(6分)解方程.
(1)3x=10﹣2x;
(2).
19.(6分)先化简,再求值:,其中x=2,y=﹣3.
20.(8分)如图,已知线段AB和点C,请用直尺和圆规作图(不要求写出作图过程,要保留作图痕迹).
(1)作射线CA、直线CB;
(2)比较大小:AC+AB CB,依据: ;
(3)在射线BC上取一点D,使CD=2AB.
21.(8分)如图,点O是直线AB上的一点,射线OC,OD在直线AB的异侧,已知OC⊥OD,OE平分∠AOC.
(1)若∠BOD=40°,求∠AOE的度数;
(2)∠AOE与∠BOD是否有可能成为对顶角?若有可能,请求出∠BOD的度数;若不可能,请说明理由.
22.(10分)如图1是1个纸杯和6个叠放在一起的纸杯的示意图,量得1个纸杯的高为10cm,6个叠放在一起的纸杯的高为14cm.
(1)问2个叠放在一起的纸杯的高是多少cm?
(2)若一批这样的纸杯按照图2的方式叠放,测得总高度为90cm,求纸杯个数.
23.(10分)在数轴上点A,B,C所表示的数分别是﹣2,6,x(x>﹣2).
(1)求AB的长;
(2)若点D是AB的中点,用含x的代数式表示CD的长;
(3)若点A以每秒5个单位的速度向左运动,同时,点B以每秒20个单位的速度向右运动,点C从原点开始以每秒1个单位的速度向右运动,记OB的中点为E,AC的中点为F,试通过计算说明的结果是定值.
24.(12分)根据以下素材,探索完成任务.
如何设计牛奶盒子?
素材1 如图1所示是长为20cm,宽为18cm的长方形包装纸,现要自制牛奶盒子.(1)上下各留宽度相同的一个长方形,中间剩余部分用于制作牛奶盒身;(2)牛奶盒身的宽与上下两个长方形的宽度和之比为3:1.
素材2 如图2,将牛奶盒身分成四块长方形,其中①③长方形大小相同,②④长方形大小也相同,且②号长方形的宽比①号多1cm.
素材3 如图3,在②号长方形上设计四个大小一样、长宽之比为6:5的长方形框,且长方形框的上下、左右间距都一样.
问题解决
任务1 分析数量关系 求图1中牛奶盒身的宽(规定:较长的边为长,较短的边为宽).
任务2 确定盒子容积 把图1中的包装纸折成图2中的牛奶盒子,求牛奶盒子的容积.
任务3 确定间距大小 求出图3中②号长方形上设计的长方形框之间的间距.
2023-2024学年浙江省丽水市莲都区七年级(上)期末数学试卷
参考答案
一、选择题(本题有10小题,每小题3分,共30分.)
1.(3分)实数﹣3的相反数是( )
A.﹣ B. C.3 D.﹣3
选:C.
2.(3分)文化和旅游部数据显示,2023年的中秋、国庆假期全国国内旅游出游人数8.26亿人次,实现国内旅游收入7534.3亿元.数据8.26亿用科学记数法表示为( )
A.8.26×109 B.82.6×108 C.8.26×108 D.82.6×107
选:C.
3.(3分)下列实数中,属于无理数的是( )
A.3.14 B. C. D.π
选:D.
4.(3分)多项式x2y﹣xy﹣1的次数和常数项分别是( )
A.3,1 B.3,﹣1 C.5,1 D.5,﹣1
选:B.
5.(3分)下列方程变形过程正确的是( )
A.由x+3=6,得x=6+3 B.由5x=3,得
C.由x+5=1,得x=5﹣1 D.由,得x=0
选:D.
6.(3分)如图,AB⊥BC,DB⊥AC,下列线段的长能表示点B到AC的距离的是( )
A.AB B.BD C.BC D.AD
选:B.
7.(3分)用代数式表示“a与b的平方的差”正确的是( )
A.a2﹣b2 B.(a﹣b)2 C.a﹣b2 D.a2﹣b
选:A.
8.(3分)下列四个式子中,计算结果最小的是( )
A.(﹣3﹣2)2 B.(﹣3)×(﹣2)2
C.﹣32÷(﹣2)2 D.﹣32﹣23
选:D.
9.(3分)2023年杭州亚运会上,我国获得奖牌383枚,其中银牌111枚,金牌数是铜牌数的3倍少12枚.若设金牌数是x,则可列出方程为( )
A.(3x﹣12)+x=383﹣111 B.3(x+12)+x=383﹣111
C. D.
选:C.
10.(3分)如图,PO是直线l的垂线段,每次在PO两侧依次增加1条线段,则第20个图形中共有三角形的数量是( )
A.820 B.840 C.40 D.20
选:A.
二、填空题(本题有6小题,每小题4分,共24分)
11.(4分)16的平方根是 ±4 .
12.(4分)用四舍五入法把1.732精确到百分位,所得的近似数是 1.73 .
13.(4分)15°30′= 15.5 °.
14.(4分)如图,表中列出了国外几个城市与北京的时差,其中带正号的数表示同一时刻比北京时间早的时数,比如北京的时间是7:00时,东京时间为8:00.则当北京的时间为2024年1月28日9:00时,纽约的时间是 2024年1月27日20:00时 .
城市 纽约 巴黎 东京 芝加哥
时差/时 ﹣13 ﹣7 +1 ﹣14
15.(4分)整式kx﹣2b的值随x的取值不同而不同,下表是当x取不同值时整式kx﹣2b对应的值,则关于x的方程kx=2(b+2)的解为 x=2 .
x ﹣2 ﹣1 0 1 2
Kx﹣2b ﹣8 ﹣5 ﹣2 1 4
16.(4分)新定义一个运算:a b=,例如2 1=22﹣2×1=2,1+2=﹣12+2×2=3.用<m>表示大于m的最小整数,例如<1>=2,<3.2>=4,<﹣3>=﹣2.按照上述规定,如果整数x满足<﹣2 3>=﹣2<1 x>+11,则x的值是 ﹣1或2 .
三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
17.(6分)计算.
(1)﹣3+7;
(2).
【解答】解:(1)原式=4;
(2)原式=﹣1+2×3+2
=﹣1+6+2
=7.
18.(6分)解方程.
(1)3x=10﹣2x;
(2).
【解答】解:(1)移项,得3x+2x=10,
合并同类项,得5x=10,
两边同除以5,得x=2.
(2)去分母,得2(3x﹣1)=12﹣(4x﹣1),
去括号,得6x﹣2=12﹣4x+1,
移项,得6x+4x=12+1+2,
合并同类项,得10x=15,
两边同除以10,得x=.
19.(6分)先化简,再求值:,其中x=2,y=﹣3.
【解答】解:原式=3x2﹣6xy﹣x2+5xy
=2x2﹣xy;
当x=2,y=﹣3时,
原式=2×22﹣2×(﹣3)=8+6=14.
20.(8分)如图,已知线段AB和点C,请用直尺和圆规作图(不要求写出作图过程,要保留作图痕迹).
(1)作射线CA、直线CB;
(2)比较大小:AC+AB > CB,依据: 两点之间线段最短 ;
(3)在射线BC上取一点D,使CD=2AB.
【解答】解:(1)如图,射线CA,直线BC即为所求;
(2)AC+AB>BC(两点之间线段最短).
故答案为:>,两点之间线段最短;
(3)如图,点D即为所求.
21.(8分)如图,点O是直线AB上的一点,射线OC,OD在直线AB的异侧,已知OC⊥OD,OE平分∠AOC.
(1)若∠BOD=40°,求∠AOE的度数;
(2)∠AOE与∠BOD是否有可能成为对顶角?若有可能,请求出∠BOD的度数;若不可能,请说明理由.
【解答】解:(1)∵OC⊥OD,
∴∠BOC+∠BOD=90°,
∴∠BOC=90°﹣∠BOD=50°,
∴∠AOC=180°﹣∠BOC=130°,
∵OE平分∠AOC,
∴∠AOE=∠AOC=65°;
(2)∠AOE与∠BOD是不可能成为对顶角,理由如下:
当∠AOE=∠BOD时,∠BOD+∠BOC+∠COE=180°,
∵OE平分∠AOC,
∴∠AOE=∠COE,
∴∠BOD=∠COE,
∵OC⊥OD,
∴∠BOC+∠BOD=90°,
∴∠BOC+∠COE=90°,
∴∠BOC+∠BOD+∠BOC+∠COE=180°,
与∠BOD+∠BOC+∠COE=180°相矛盾,
∴∠AOE与∠BOD是不可能成为对顶角.
22.(10分)如图1是1个纸杯和6个叠放在一起的纸杯的示意图,量得1个纸杯的高为10cm,6个叠放在一起的纸杯的高为14cm.
(1)问2个叠放在一起的纸杯的高是多少cm?
(2)若一批这样的纸杯按照图2的方式叠放,测得总高度为90cm,求纸杯个数.
【解答】解:(1)根据题意得:
10+(14﹣10)÷5
=10+4÷5
=10.8(cm),
则2个叠放在一起的纸杯的高是10.8cm;
(2)根据题意得:
(90﹣10)÷0.8+1
=80÷0.8+1
=101(个),
则纸杯个数为101个.
23.(10分)在数轴上点A,B,C所表示的数分别是﹣2,6,x(x>﹣2).
(1)求AB的长;
(2)若点D是AB的中点,用含x的代数式表示CD的长;
(3)若点A以每秒5个单位的速度向左运动,同时,点B以每秒20个单位的速度向右运动,点C从原点开始以每秒1个单位的速度向右运动,记OB的中点为E,AC的中点为F,试通过计算说明的结果是定值.
【解答】解:(1)因为点A,B所表示的数分别是﹣2,6,
所以AB=6﹣(﹣2)=8.
(2)因为点D是AB的中点,
所以,
则点D表示的数是2.
当﹣2<x≤2时,
CD=2﹣x.
当x>2时,
CD=x﹣2.
(3)设运动的时间为t,
则点C运动后对应点所表示的数为t,点A运动后对应点所表示的数为﹣2﹣5t,点B运动后对应点所表示的数为6+20t,
因为OB的中点为E,
所以点E所表示的数为3+10t.
因为AC中点为F,
所以点F所表示的数为﹣1﹣2t,
所以AB=6+20t﹣(﹣2﹣5t)=8+25t,OC=t,EF=4+12t,
所以=.
24.(12分)根据以下素材,探索完成任务.
如何设计牛奶盒子?
素材1 如图1所示是长为20cm,宽为18cm的长方形包装纸,现要自制牛奶盒子.(1)上下各留宽度相同的一个长方形,中间剩余部分用于制作牛奶盒身;(2)牛奶盒身的宽与上下两个长方形的宽度和之比为3:1.
素材2 如图2,将牛奶盒身分成四块长方形,其中①③长方形大小相同,②④长方形大小也相同,且②号长方形的宽比①号多1cm.
素材3 如图3,在②号长方形上设计四个大小一样、长宽之比为6:5的长方形框,且长方形框的上下、左右间距都一样.
问题解决
任务1 分析数量关系 求图1中牛奶盒身的宽(规定:较长的边为长,较短的边为宽).
任务2 确定盒子容积 把图1中的包装纸折成图2中的牛奶盒子,求牛奶盒子的容积.
任务3 确定间距大小 求出图3中②号长方形上设计的长方形框之间的间距.
【解答】解:任务一:20÷(3+1)×3=15(cm),
15cm<18cm,
答:牛奶盒身的宽是15cm.
任务二:(18﹣2)÷4=4(cm),
4+1=5(cm),
V=15×4×5=300(cm3),
答:牛奶盒子的容积是300cm3,
任务三:设长方形框长为6x cm,宽为5x cm,
(5﹣6x)÷2=(15﹣4×5x)÷5
解得:x=0.5,
(5﹣6×0.5)÷2=1(cm),
答:长方形框之间的间距为1cm.
同课章节目录
