小升初分班考重点专题特训:比与比例(含答案)-数学六年级下册北师大版
文档属性
| 名称 | 小升初分班考重点专题特训:比与比例(含答案)-数学六年级下册北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 530.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-13 17:31:19 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
绝密★启用前
小升初分班考重点专题特训:比与比例-数学六年级下册北师大版
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题
1.能与∶组成比例的是( )。
A.1.2∶0.8 B.2∶3 C.0.9∶1.2 D.4∶6
2.一种微型零件的长是5毫米,画在图纸上长2厘米,这张图纸的比例尺是( )。
A.40∶1 B.4∶1 C.1∶4 D.1∶40
3.下面2个长方形的面积相等,根据它们边的关系写出的比例正确的是( )。
A.8∶a=9∶b B.8∶9=a∶b C.8∶9=b∶a D.9∶a=b∶8
4.一项公路施工,A单独做5天完成,B单独做6天完成,A、B工作效率的比是( )。
A.6∶5 B.5∶6 C.5∶ D.∶
5.下面哪个问题不能用解答?( )
A.少先队员采集植物标本120件,昆虫标本数量比植物标本多,求采集的昆虫标本数量。
B.食堂准备包120个饺子,已经包了其中的,还剩下多少个饺子没包?
C.五年级有120人,六年级人数比五年级少,六年级有多少人?
D.爸爸从成都开车去乐山,全长约120千米,已行路程与未行路程的比是1∶7,那么距离乐山还有多少千米?
6.如图,两个圆重叠部分的面积相当于甲面积的,相当于乙面积的,那么甲和乙面积的最简整数比是( )。
A.3∶2 B.2∶3 C.5∶4 D.4∶5
二、填空题
7.给5、、0.8再配上一个数,使这四个数组成比例,这个数最大是( )。
8.比例尺10∶1,表示图上距离1厘米相当于实际距离( )厘米。
9.甲走的路程比乙走的路程多,乙用的时间比甲用的时间多。甲、乙速度的比是( )∶( )。
10.甲、乙、丙三个数的平均数是15,甲、乙、丙三个数的比是2∶3∶4,甲数是( )。
11.A比B少20%,则A与B的比是( ),B比A多( )%。
12.妈妈和王阿姨一起去超市买菜,妈妈花4元买了2kg西红柿,王阿姨买了3kg西红柿花去6元。
(1)请你根据以上信息写出两个比:( )和( )。
(2)这两个比( )组成比例(填“能”或“不能”),我的判断理由是 。
三、判断题
13.比值是的比有无数个。( )
14.将50克糖溶入200克水中,糖与糖水的比是1∶4。( )
15.把1.2吨∶350千克化成最简单的整数比是24∶7。( )
16.A∶B=,那么(A×2)∶(B×2)=。( )
17.两个正方形的边长之比是2∶1,这两个正方形的面积之比也是2∶1。( )
18.男生人数与女生人数的比是7∶3,已知男生有21人,则女生有9人。( )
四、解答题
19.李明在电脑上把一张长6厘米,宽4厘米的照片按比例放大,放大后照片的长是13.5厘米,宽是多少厘米?
20.某加油站95号汽油每升8.2元,油价下调后每升8元,原来加60升95号汽油的钱调价后可以给汽车加油多少升?(用比例知识解答)
21.甲、乙两个粮仓共存储了4200吨粮食,运走甲粮仓的50%和乙粮仓的后,甲、乙粮仓的存粮量之比是2∶1。甲、乙两个粮仓原来分别有粮食多少吨?
22.在比例尺是1∶400000的地图上,测得甲、乙两城距离是4.5厘米,若把它画在1∶600000的地图上,甲、乙两城长多少厘米?
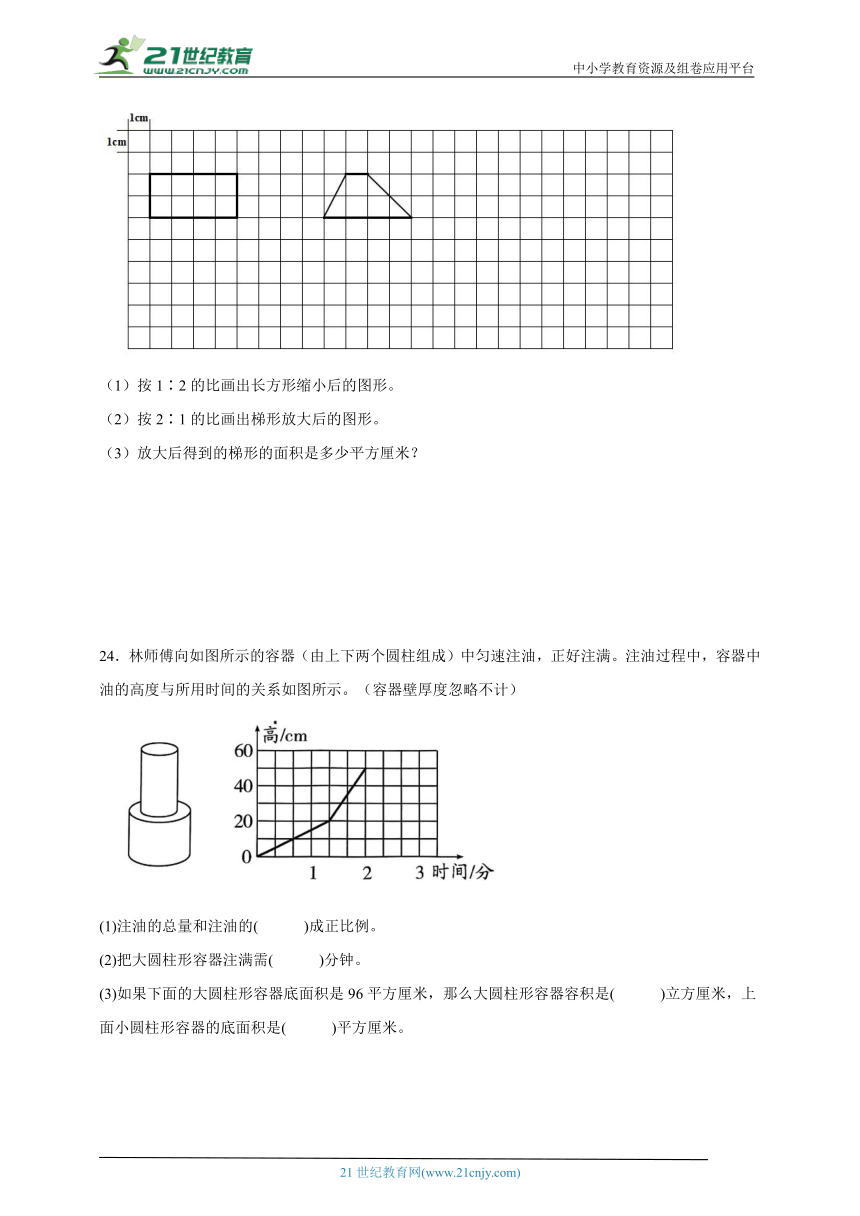
23.操作。
(1)按1∶2的比画出长方形缩小后的图形。
(2)按2∶1的比画出梯形放大后的图形。
(3)放大后得到的梯形的面积是多少平方厘米?
24.林师傅向如图所示的容器(由上下两个圆柱组成)中匀速注油,正好注满。注油过程中,容器中油的高度与所用时间的关系如图所示。(容器壁厚度忽略不计)
(1)注油的总量和注油的( )成正比例。
(2)把大圆柱形容器注满需( )分钟。
(3)如果下面的大圆柱形容器底面积是96平方厘米,那么大圆柱形容器容积是( )立方厘米,上面小圆柱形容器的底面积是( )平方厘米。
参考答案:
1.A
【分析】比值相等的两个比可以组成比例。∶的比值是1.5,分别计算出各个选项的比值,然后与1.5比较即可,据此解答。
【详解】A.1.2∶0.8=1.2÷0.8=1.5,与题干中比的比值相等;
B.2∶3=2÷3=,与题干中比的比值不相等;
C. 0.9∶1.2=0.9÷1.2=0.75,与题干中比的比值不相等;
D. 4∶6=4÷6=,与题干中比的比值不相等。
故答案为:A
2.B
【分析】1厘米=10毫米,据此先统一单位。比例尺=图上距离∶实际距离,据此求出这张图纸的比例尺。
【详解】2厘米=20毫米
20∶5
=(20÷5)∶(5÷5)
=4∶1
所以,这张图纸的比例尺是4∶1。
故答案为:B
3.C
【分析】长方形面积=长×宽,2个长方形的面积相等,由此可以写出8a=9b,根据比例的基本性质,比例的两内项积=两外项积,将各选项比例写成两内项积=两外项积的形式,得到8a=9b的比例正确。
【详解】8a=9b
A.8∶a=9∶b,根据比例的基本性质,可得8b=9a,排除;
B.8∶9=a∶b,根据比例的基本性质,可得8b=9a,排除;
C.8∶9=b∶a,根据比例的基本性质,可得8a=9b,正确;
D.9∶a=b∶8,根据比例的基本性质,可得ab=9×8,排除。
根据它们边的关系写出的比例正确的是8∶9=b∶a。
故答案为:C
4.A
【分析】根据工作效率工作总量工作时间,把这项工程看成单位,的工作效率为:,的工作效率为:,A、B工作效率的比是化简即可,据此选择。
【详解】
=︰=6︰5。
故答案为:A
【点睛】本题考查比的意义和化简,学生需熟练掌握。
5.A
【分析】A.已知植物标本有120件,昆虫标本数量比植物标本多,把植物标本数量看作单位“1”,则昆虫标本数量是植物标本数量的,单位“1”已知,根据分数乘法的意义求出昆虫标本数量。
B.已知食堂准备包120个饺子,已经包了其中的,把准备包饺子的总数看作单位“1”,则还剩下总数的,单位“1”已知,根据分数乘法的意义求出还剩下没包的饺子。
C.已知五年级有120人,六年级人数比五年级少,把五年级人数看作单位“1”,则六年级人数是五年级的,单位“1”已知,根据分数乘法的意义求出六年级人数。
D.已知全长约120千米,已行路程与未行路程的比是1∶7,即未行路程占全程的,把全程看作单位“1”,单位“1”已知,根据分数乘法的意义求出未行的路程。
【详解】A.求采集的昆虫标本数量,列式为:,不能用解答;
B.求还剩下多少个饺子没包,列式为:,能用解答;
C.求六年级有多少人,列式为:,能用解答;
D.求距离乐山还有多少千米,列式为:,能用解答。
故答案为:A
6.A
【分析】分别将两个圆的面积看作单位“1”,假设重叠部分的面积是1,用重叠部分的面积÷对应分率,分别求出两个圆的面积,两数相除又叫两个数的比,根据比的意义,写出甲乙面积比,化简即可。
【详解】假设重叠部分的面积是1。
(1÷)∶(1÷)
=∶5
=(×2)∶(5×2)
=15∶10
=(15÷5)∶(10÷5)
=3∶2
甲和乙面积的最简整数比是3∶2。
故答案为:A
7.
【分析】根据比例的基本性质:比例的两个内项之积等于两个外项之积;要使这个数最大,这个数应该和相乘,则内外项之积应是5×0.8=4,再除以,即可解答。
【详解】5×0.8÷
=4÷
=4×
=
给5、、0.8再配上一个数,使这四个数组成比例,这个数最大是。
8.0.1
【分析】根据实际距离=图上距离÷比例尺,代入数据,即可解答。
【详解】1÷
=1×
=0.1(厘米)
比例尺10∶1,表示图上距离1厘米相当于实际距离0.1厘米。
9. 5 3
【分析】将乙走的路程看作单位“1”,则甲走的路程是(1+);将甲用的时间看作单位“1”,则乙用的时间是(1+),根据路程÷时间=速度,分别求出甲和乙的速度,两数相除又叫两个数的比,根据比的意义,写出甲乙速度比,化简即可。
【详解】甲走的路程:1+=
乙用的时间:1+=
甲的速度:÷1=
乙的速度:1÷=
甲、乙速度的比:∶=(×15)∶(×15)=20∶12=(20÷4)∶(12÷4)=5∶3
甲、乙速度的比是5∶3。
【点睛】关键是理解速度、时间、路程之间的关系,通过分率确定甲乙速度比。
10.10
【分析】用15×3,求出甲、乙、丙三个数的和;再根据甲、乙、丙三个数的比是2∶3∶4,即把甲、乙、丙三个数的和分成了2+3+4=9份,再用甲、乙、丙三个数的和除以总份数,求出1份是多少,进而求出甲数的值。
【详解】2+3+4
=5+4
=9(份)
15×3÷9×2
=45÷9×2
=5×2
=10
甲、乙、丙三个数的平均数是15,甲、乙、丙三个数的比是2∶3∶4,甲数是10。
11. 4∶5 25
【分析】假设B为100,已知A比B少20%,把B看作单位“1”,A是B的(1-20%),根据百分数乘法的意义,用100×(1-20%)即可求出A,然后写出A与B的比,再化简即可;求一个数比另一个数多百分之几,用相差数除以另一个数再乘100%,则用B减去A的差除以A,再乘100%,即可求出B比A多百分之几。
【详解】假设B为100,
A:100×(1-20%)
=100×80%
=80
80∶100
=(80÷20)∶(100÷20)
=4∶5
(100-80)÷80×100%
=20÷80×100%
=25%
A比B少20%,则A与B的比是4∶5,B比A多25%。
12.(1) 4∶2 6∶3
(2) 能 这两个比的比值相等
【分析】(1)两个量相除,叫做两个量的比。从题意可知:可以用总价∶数量,也可以总价∶总价,数量∶数量。
(2)表示两个比相等的式子,叫做比例。计算出两个比的比值,只要比值相等就能组成比例。
【详解】(1)根据总价∶数量可得,4∶2、6∶3
(答案不唯一)
(2)4∶2=4÷2=2
6∶3=6÷3=2
4∶2 =6∶3
这两个比能组成比例,我的判断理由是:因为这两个比的比值相等,这个比值也就是单价一样,都是每千克2元。
(答案不唯一)
13.√
【分析】根据求比值的意义可知,比值是的比有无数个,如:1∶3、2∶6、3∶9等。
【详解】比值是的比有无数个。原题说法正确。
故答案为:√
14.×
【分析】将50克糖溶入200克水中,形成的糖水为(50+200)克,先根据比的意义,写出糖与糖水的比;再根据比的基本性质化成最简整数比。据此判断。
【详解】50∶(50+200)
=50∶250
=(50÷50)∶(250÷50)
=1∶5
所以糖与糖水的比是1∶5,故原说法错误。
故答案为:×
15.√
【分析】先把1.2吨∶350千克的前项和后项统一单位,即1.2吨∶350千克=1200千克∶350千克;再根据比的基本性质,即比的前项和后项同时乘或除以一个相同的数(0除外)比值不变,把比1200∶350化成最简整数比。据此判断即可。
【详解】1.2吨∶350千克
=1200千克∶350千克
=1200∶350
=(1200÷50)∶(350÷50)
=24∶7
把1.2吨∶350千克化成最简单的整数比是24∶7,所以原题说法正确。
故答案为:√
16.×
【分析】根据比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。据此解答即可。
【详解】A∶B=,那么(A×2)∶(B×2)=;所以原题说法错误。
故答案为:×
17.×
【分析】由题意可知,两个正方的边长之比是2∶1,则假设这两个正方形的边长分别是2和1,然后根据正方形的面积公式:S=a2,据此分别求出两个正方形的面积,进而求出这两个正方形的面积之比。
【详解】假设这两个正方形的边长分别是2和1
(2×2)∶(1×1)
=4∶1
则这两个正方形的面积之比也是4∶1。原题干说法错误。
故答案为:×
18.√
【分析】根据题意,男生人数与女生人数的比是7∶3,可以把男生人数看作7份,女生人数看作3份;用男生人数除以男生占的份数,求出一份数,再用一份数乘女生占的份数,即可求出女生人数,据此判断。
【详解】一份数:21÷7=3(人)
女生:3×3=9(人)
男生人数与女生人数的比是7∶3,已知男生有21人,则女生有9人。
原题说法正确。
故答案为:√
【点睛】本题考查比的应用,把比看作份数,求出一份数是解题的关键。
19.9厘米
【分析】根据题意,照片按比例放大,则放大前后长边的比值与放大前后宽边的比值相等,即放大后的长边∶放大前的长边=放大后的宽边∶放大前的宽边,据此列出正比例方程,并求解。
【详解】解:设宽是厘米。
13.5∶6=∶4
6=13.5×4
6=54
6÷6=54÷6
=9
答:宽是9厘米。
【点睛】明确照片放大前后对应边的比值一定,是解题的关键。
20.61.5升
【分析】油价调整前后,钱总数不变。总价一定时,数量和单价成反比例关系。据此,将调价后可以给汽车加油多少升设为未知数,从而列出比例解比例即可。
【详解】解:设调价后可以给汽车加油x升。
x∶60=8.2∶8
8x=60×8.2
8x=492
8x÷8=492÷8
x=61.5
答:调价后可以给汽车加油61.5升。
【点睛】本题考查了反比例的应用,解题关键是找出比例关系列比例。
21.甲粮仓:2400吨;乙粮仓:1800吨
【分析】根据题意,设甲粮仓原有粮食x吨,则乙粮仓原有粮食(4200-x)吨,甲粮仓运走50%,还剩(1-50%)×x吨;乙粮仓运走后,还剩(4200-x)×(1-),运走甲粮仓的50%和乙粮仓的后,甲、乙粮仓的存粮之比是2∶1,列方程(1-50%)×x∶(4200-x)×(1-)=2∶1,解比例,即可解答。
【详解】解:设甲粮仓原来有粮食x吨,则乙粮仓原来有粮食(4200-x)吨。
(1-50%)×x∶(4200-x)×(1-)=2∶1
50%x∶(4200-x)×=2∶1
0.5x=2×(4200-x)×
0.5x=2800-x
x+x=2800
x=2800
x=2800÷
x=2800×
x=2400
乙粮仓:4200-2400=1800(吨)
答:甲粮仓原来有粮食2400吨,乙粮仓原来有粮食1800吨。
【点睛】根据方程的实际应用以及比例的意义,找出甲粮仓与乙粮仓之间存粮食之间的关系,设出未知数,找出它们之间的关系量,列比例,解比例。
22.3厘米
【分析】在比例尺是1∶400000的地图上,测得甲、乙两城距离是4.5厘米,用图上距离除以比例尺,计算出甲、乙两城的实际距离,再根据图上距离=实际距离×比例尺,计算在1∶600000的地图上,甲、乙两城的图上距离。
【详解】
(厘米)
(厘米)
答:在1∶600000的地图上,甲、乙两城长3厘米。
23.(1)(2)见详解
(3)20平方厘米
【分析】(1)长方形的长是4厘米,宽是2厘米,按1∶2的比缩小后,长是厘米,宽是厘米,据此画出缩小后的长方形。
(2)梯形的上底是1厘米,下底是4厘米,高是2厘米,按2∶1的比放大后,梯形的上底是厘米,下底是厘米,高是厘米,据此画出放大后的梯形。
(3)根据梯形的面积=(上底+下底)×高÷2,代入数据计算即可。
【详解】(1)(2)如图:
(3)放大后得到的梯形的上底是2厘米,下底是8厘米,高是4厘米,
(平方厘米)
答:放大后得到的梯形的面积是20平方厘米。
24.(1)时间
(2)
(3) 1920 32
【分析】(1)由图中可以看出容器中油的高度与所用时间的关系是时间越长,容器中油的高度越高,因此注油的总量越大;
(2)由图中可以看出在注油高度是20cm时,大圆柱形容器注满。由图中也可以看出把1分钟平均成三份,每份是,而20cm对应的时间是分钟;
(3)从题图上看,大圆柱里油高20厘米,大圆柱容积是96×20=1920(立方厘米);从题图上看,小圆柱的容积是1920÷×(2 )=960(平方厘米),高是50 20=30(厘米),再用960÷30求出底面积。
【详解】(1)注油的总量和注油的时间成正比例。
(2)
(3)大圆柱容积:96×20=1920(立方厘米)
小圆柱的容积:1920÷×(2 )=960(平方厘米)
高:50 20=30(厘米)
小圆柱底面积:960÷30=32(平方厘米)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
绝密★启用前
小升初分班考重点专题特训:比与比例-数学六年级下册北师大版
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题
1.能与∶组成比例的是( )。
A.1.2∶0.8 B.2∶3 C.0.9∶1.2 D.4∶6
2.一种微型零件的长是5毫米,画在图纸上长2厘米,这张图纸的比例尺是( )。
A.40∶1 B.4∶1 C.1∶4 D.1∶40
3.下面2个长方形的面积相等,根据它们边的关系写出的比例正确的是( )。
A.8∶a=9∶b B.8∶9=a∶b C.8∶9=b∶a D.9∶a=b∶8
4.一项公路施工,A单独做5天完成,B单独做6天完成,A、B工作效率的比是( )。
A.6∶5 B.5∶6 C.5∶ D.∶
5.下面哪个问题不能用解答?( )
A.少先队员采集植物标本120件,昆虫标本数量比植物标本多,求采集的昆虫标本数量。
B.食堂准备包120个饺子,已经包了其中的,还剩下多少个饺子没包?
C.五年级有120人,六年级人数比五年级少,六年级有多少人?
D.爸爸从成都开车去乐山,全长约120千米,已行路程与未行路程的比是1∶7,那么距离乐山还有多少千米?
6.如图,两个圆重叠部分的面积相当于甲面积的,相当于乙面积的,那么甲和乙面积的最简整数比是( )。
A.3∶2 B.2∶3 C.5∶4 D.4∶5
二、填空题
7.给5、、0.8再配上一个数,使这四个数组成比例,这个数最大是( )。
8.比例尺10∶1,表示图上距离1厘米相当于实际距离( )厘米。
9.甲走的路程比乙走的路程多,乙用的时间比甲用的时间多。甲、乙速度的比是( )∶( )。
10.甲、乙、丙三个数的平均数是15,甲、乙、丙三个数的比是2∶3∶4,甲数是( )。
11.A比B少20%,则A与B的比是( ),B比A多( )%。
12.妈妈和王阿姨一起去超市买菜,妈妈花4元买了2kg西红柿,王阿姨买了3kg西红柿花去6元。
(1)请你根据以上信息写出两个比:( )和( )。
(2)这两个比( )组成比例(填“能”或“不能”),我的判断理由是 。
三、判断题
13.比值是的比有无数个。( )
14.将50克糖溶入200克水中,糖与糖水的比是1∶4。( )
15.把1.2吨∶350千克化成最简单的整数比是24∶7。( )
16.A∶B=,那么(A×2)∶(B×2)=。( )
17.两个正方形的边长之比是2∶1,这两个正方形的面积之比也是2∶1。( )
18.男生人数与女生人数的比是7∶3,已知男生有21人,则女生有9人。( )
四、解答题
19.李明在电脑上把一张长6厘米,宽4厘米的照片按比例放大,放大后照片的长是13.5厘米,宽是多少厘米?
20.某加油站95号汽油每升8.2元,油价下调后每升8元,原来加60升95号汽油的钱调价后可以给汽车加油多少升?(用比例知识解答)
21.甲、乙两个粮仓共存储了4200吨粮食,运走甲粮仓的50%和乙粮仓的后,甲、乙粮仓的存粮量之比是2∶1。甲、乙两个粮仓原来分别有粮食多少吨?
22.在比例尺是1∶400000的地图上,测得甲、乙两城距离是4.5厘米,若把它画在1∶600000的地图上,甲、乙两城长多少厘米?
23.操作。
(1)按1∶2的比画出长方形缩小后的图形。
(2)按2∶1的比画出梯形放大后的图形。
(3)放大后得到的梯形的面积是多少平方厘米?
24.林师傅向如图所示的容器(由上下两个圆柱组成)中匀速注油,正好注满。注油过程中,容器中油的高度与所用时间的关系如图所示。(容器壁厚度忽略不计)
(1)注油的总量和注油的( )成正比例。
(2)把大圆柱形容器注满需( )分钟。
(3)如果下面的大圆柱形容器底面积是96平方厘米,那么大圆柱形容器容积是( )立方厘米,上面小圆柱形容器的底面积是( )平方厘米。
参考答案:
1.A
【分析】比值相等的两个比可以组成比例。∶的比值是1.5,分别计算出各个选项的比值,然后与1.5比较即可,据此解答。
【详解】A.1.2∶0.8=1.2÷0.8=1.5,与题干中比的比值相等;
B.2∶3=2÷3=,与题干中比的比值不相等;
C. 0.9∶1.2=0.9÷1.2=0.75,与题干中比的比值不相等;
D. 4∶6=4÷6=,与题干中比的比值不相等。
故答案为:A
2.B
【分析】1厘米=10毫米,据此先统一单位。比例尺=图上距离∶实际距离,据此求出这张图纸的比例尺。
【详解】2厘米=20毫米
20∶5
=(20÷5)∶(5÷5)
=4∶1
所以,这张图纸的比例尺是4∶1。
故答案为:B
3.C
【分析】长方形面积=长×宽,2个长方形的面积相等,由此可以写出8a=9b,根据比例的基本性质,比例的两内项积=两外项积,将各选项比例写成两内项积=两外项积的形式,得到8a=9b的比例正确。
【详解】8a=9b
A.8∶a=9∶b,根据比例的基本性质,可得8b=9a,排除;
B.8∶9=a∶b,根据比例的基本性质,可得8b=9a,排除;
C.8∶9=b∶a,根据比例的基本性质,可得8a=9b,正确;
D.9∶a=b∶8,根据比例的基本性质,可得ab=9×8,排除。
根据它们边的关系写出的比例正确的是8∶9=b∶a。
故答案为:C
4.A
【分析】根据工作效率工作总量工作时间,把这项工程看成单位,的工作效率为:,的工作效率为:,A、B工作效率的比是化简即可,据此选择。
【详解】
=︰=6︰5。
故答案为:A
【点睛】本题考查比的意义和化简,学生需熟练掌握。
5.A
【分析】A.已知植物标本有120件,昆虫标本数量比植物标本多,把植物标本数量看作单位“1”,则昆虫标本数量是植物标本数量的,单位“1”已知,根据分数乘法的意义求出昆虫标本数量。
B.已知食堂准备包120个饺子,已经包了其中的,把准备包饺子的总数看作单位“1”,则还剩下总数的,单位“1”已知,根据分数乘法的意义求出还剩下没包的饺子。
C.已知五年级有120人,六年级人数比五年级少,把五年级人数看作单位“1”,则六年级人数是五年级的,单位“1”已知,根据分数乘法的意义求出六年级人数。
D.已知全长约120千米,已行路程与未行路程的比是1∶7,即未行路程占全程的,把全程看作单位“1”,单位“1”已知,根据分数乘法的意义求出未行的路程。
【详解】A.求采集的昆虫标本数量,列式为:,不能用解答;
B.求还剩下多少个饺子没包,列式为:,能用解答;
C.求六年级有多少人,列式为:,能用解答;
D.求距离乐山还有多少千米,列式为:,能用解答。
故答案为:A
6.A
【分析】分别将两个圆的面积看作单位“1”,假设重叠部分的面积是1,用重叠部分的面积÷对应分率,分别求出两个圆的面积,两数相除又叫两个数的比,根据比的意义,写出甲乙面积比,化简即可。
【详解】假设重叠部分的面积是1。
(1÷)∶(1÷)
=∶5
=(×2)∶(5×2)
=15∶10
=(15÷5)∶(10÷5)
=3∶2
甲和乙面积的最简整数比是3∶2。
故答案为:A
7.
【分析】根据比例的基本性质:比例的两个内项之积等于两个外项之积;要使这个数最大,这个数应该和相乘,则内外项之积应是5×0.8=4,再除以,即可解答。
【详解】5×0.8÷
=4÷
=4×
=
给5、、0.8再配上一个数,使这四个数组成比例,这个数最大是。
8.0.1
【分析】根据实际距离=图上距离÷比例尺,代入数据,即可解答。
【详解】1÷
=1×
=0.1(厘米)
比例尺10∶1,表示图上距离1厘米相当于实际距离0.1厘米。
9. 5 3
【分析】将乙走的路程看作单位“1”,则甲走的路程是(1+);将甲用的时间看作单位“1”,则乙用的时间是(1+),根据路程÷时间=速度,分别求出甲和乙的速度,两数相除又叫两个数的比,根据比的意义,写出甲乙速度比,化简即可。
【详解】甲走的路程:1+=
乙用的时间:1+=
甲的速度:÷1=
乙的速度:1÷=
甲、乙速度的比:∶=(×15)∶(×15)=20∶12=(20÷4)∶(12÷4)=5∶3
甲、乙速度的比是5∶3。
【点睛】关键是理解速度、时间、路程之间的关系,通过分率确定甲乙速度比。
10.10
【分析】用15×3,求出甲、乙、丙三个数的和;再根据甲、乙、丙三个数的比是2∶3∶4,即把甲、乙、丙三个数的和分成了2+3+4=9份,再用甲、乙、丙三个数的和除以总份数,求出1份是多少,进而求出甲数的值。
【详解】2+3+4
=5+4
=9(份)
15×3÷9×2
=45÷9×2
=5×2
=10
甲、乙、丙三个数的平均数是15,甲、乙、丙三个数的比是2∶3∶4,甲数是10。
11. 4∶5 25
【分析】假设B为100,已知A比B少20%,把B看作单位“1”,A是B的(1-20%),根据百分数乘法的意义,用100×(1-20%)即可求出A,然后写出A与B的比,再化简即可;求一个数比另一个数多百分之几,用相差数除以另一个数再乘100%,则用B减去A的差除以A,再乘100%,即可求出B比A多百分之几。
【详解】假设B为100,
A:100×(1-20%)
=100×80%
=80
80∶100
=(80÷20)∶(100÷20)
=4∶5
(100-80)÷80×100%
=20÷80×100%
=25%
A比B少20%,则A与B的比是4∶5,B比A多25%。
12.(1) 4∶2 6∶3
(2) 能 这两个比的比值相等
【分析】(1)两个量相除,叫做两个量的比。从题意可知:可以用总价∶数量,也可以总价∶总价,数量∶数量。
(2)表示两个比相等的式子,叫做比例。计算出两个比的比值,只要比值相等就能组成比例。
【详解】(1)根据总价∶数量可得,4∶2、6∶3
(答案不唯一)
(2)4∶2=4÷2=2
6∶3=6÷3=2
4∶2 =6∶3
这两个比能组成比例,我的判断理由是:因为这两个比的比值相等,这个比值也就是单价一样,都是每千克2元。
(答案不唯一)
13.√
【分析】根据求比值的意义可知,比值是的比有无数个,如:1∶3、2∶6、3∶9等。
【详解】比值是的比有无数个。原题说法正确。
故答案为:√
14.×
【分析】将50克糖溶入200克水中,形成的糖水为(50+200)克,先根据比的意义,写出糖与糖水的比;再根据比的基本性质化成最简整数比。据此判断。
【详解】50∶(50+200)
=50∶250
=(50÷50)∶(250÷50)
=1∶5
所以糖与糖水的比是1∶5,故原说法错误。
故答案为:×
15.√
【分析】先把1.2吨∶350千克的前项和后项统一单位,即1.2吨∶350千克=1200千克∶350千克;再根据比的基本性质,即比的前项和后项同时乘或除以一个相同的数(0除外)比值不变,把比1200∶350化成最简整数比。据此判断即可。
【详解】1.2吨∶350千克
=1200千克∶350千克
=1200∶350
=(1200÷50)∶(350÷50)
=24∶7
把1.2吨∶350千克化成最简单的整数比是24∶7,所以原题说法正确。
故答案为:√
16.×
【分析】根据比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。据此解答即可。
【详解】A∶B=,那么(A×2)∶(B×2)=;所以原题说法错误。
故答案为:×
17.×
【分析】由题意可知,两个正方的边长之比是2∶1,则假设这两个正方形的边长分别是2和1,然后根据正方形的面积公式:S=a2,据此分别求出两个正方形的面积,进而求出这两个正方形的面积之比。
【详解】假设这两个正方形的边长分别是2和1
(2×2)∶(1×1)
=4∶1
则这两个正方形的面积之比也是4∶1。原题干说法错误。
故答案为:×
18.√
【分析】根据题意,男生人数与女生人数的比是7∶3,可以把男生人数看作7份,女生人数看作3份;用男生人数除以男生占的份数,求出一份数,再用一份数乘女生占的份数,即可求出女生人数,据此判断。
【详解】一份数:21÷7=3(人)
女生:3×3=9(人)
男生人数与女生人数的比是7∶3,已知男生有21人,则女生有9人。
原题说法正确。
故答案为:√
【点睛】本题考查比的应用,把比看作份数,求出一份数是解题的关键。
19.9厘米
【分析】根据题意,照片按比例放大,则放大前后长边的比值与放大前后宽边的比值相等,即放大后的长边∶放大前的长边=放大后的宽边∶放大前的宽边,据此列出正比例方程,并求解。
【详解】解:设宽是厘米。
13.5∶6=∶4
6=13.5×4
6=54
6÷6=54÷6
=9
答:宽是9厘米。
【点睛】明确照片放大前后对应边的比值一定,是解题的关键。
20.61.5升
【分析】油价调整前后,钱总数不变。总价一定时,数量和单价成反比例关系。据此,将调价后可以给汽车加油多少升设为未知数,从而列出比例解比例即可。
【详解】解:设调价后可以给汽车加油x升。
x∶60=8.2∶8
8x=60×8.2
8x=492
8x÷8=492÷8
x=61.5
答:调价后可以给汽车加油61.5升。
【点睛】本题考查了反比例的应用,解题关键是找出比例关系列比例。
21.甲粮仓:2400吨;乙粮仓:1800吨
【分析】根据题意,设甲粮仓原有粮食x吨,则乙粮仓原有粮食(4200-x)吨,甲粮仓运走50%,还剩(1-50%)×x吨;乙粮仓运走后,还剩(4200-x)×(1-),运走甲粮仓的50%和乙粮仓的后,甲、乙粮仓的存粮之比是2∶1,列方程(1-50%)×x∶(4200-x)×(1-)=2∶1,解比例,即可解答。
【详解】解:设甲粮仓原来有粮食x吨,则乙粮仓原来有粮食(4200-x)吨。
(1-50%)×x∶(4200-x)×(1-)=2∶1
50%x∶(4200-x)×=2∶1
0.5x=2×(4200-x)×
0.5x=2800-x
x+x=2800
x=2800
x=2800÷
x=2800×
x=2400
乙粮仓:4200-2400=1800(吨)
答:甲粮仓原来有粮食2400吨,乙粮仓原来有粮食1800吨。
【点睛】根据方程的实际应用以及比例的意义,找出甲粮仓与乙粮仓之间存粮食之间的关系,设出未知数,找出它们之间的关系量,列比例,解比例。
22.3厘米
【分析】在比例尺是1∶400000的地图上,测得甲、乙两城距离是4.5厘米,用图上距离除以比例尺,计算出甲、乙两城的实际距离,再根据图上距离=实际距离×比例尺,计算在1∶600000的地图上,甲、乙两城的图上距离。
【详解】
(厘米)
(厘米)
答:在1∶600000的地图上,甲、乙两城长3厘米。
23.(1)(2)见详解
(3)20平方厘米
【分析】(1)长方形的长是4厘米,宽是2厘米,按1∶2的比缩小后,长是厘米,宽是厘米,据此画出缩小后的长方形。
(2)梯形的上底是1厘米,下底是4厘米,高是2厘米,按2∶1的比放大后,梯形的上底是厘米,下底是厘米,高是厘米,据此画出放大后的梯形。
(3)根据梯形的面积=(上底+下底)×高÷2,代入数据计算即可。
【详解】(1)(2)如图:
(3)放大后得到的梯形的上底是2厘米,下底是8厘米,高是4厘米,
(平方厘米)
答:放大后得到的梯形的面积是20平方厘米。
24.(1)时间
(2)
(3) 1920 32
【分析】(1)由图中可以看出容器中油的高度与所用时间的关系是时间越长,容器中油的高度越高,因此注油的总量越大;
(2)由图中可以看出在注油高度是20cm时,大圆柱形容器注满。由图中也可以看出把1分钟平均成三份,每份是,而20cm对应的时间是分钟;
(3)从题图上看,大圆柱里油高20厘米,大圆柱容积是96×20=1920(立方厘米);从题图上看,小圆柱的容积是1920÷×(2 )=960(平方厘米),高是50 20=30(厘米),再用960÷30求出底面积。
【详解】(1)注油的总量和注油的时间成正比例。
(2)
(3)大圆柱容积:96×20=1920(立方厘米)
小圆柱的容积:1920÷×(2 )=960(平方厘米)
高:50 20=30(厘米)
小圆柱底面积:960÷30=32(平方厘米)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
