湖北省潜江市2023-2024学年七年级下学期期末数学试卷(含详解)
文档属性
| 名称 | 湖北省潜江市2023-2024学年七年级下学期期末数学试卷(含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-12 00:00:00 | ||
图片预览



文档简介
湖北省潜江市2023-2024学年七年级下学期期末数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列调查中,适合进行普查的是( )
A.了解《中国诗词大会》的收视率 B.调查一批灯泡的使用寿命
C.了解七(1)班学生的身高情况 D.调查某品牌笔芯的使用寿命
2.下列说法中,正确的是( )
A.1的立方根是 B.的平方根是2
C.负数没有立方根 D.9的算术平方根是3
3.在下列命题中,为真命题的是( )
A.相等的角是对顶角
B.平行于同一条直线的两条直线互相平行
C.同旁内角互补
D.垂直于同一条直线的两条直线互相垂直
4.一个一元一次不等式组的解集在数轴上表示如图所示,则该不等式组的解集为( )
A. B. C. D.
5.设,a在两个相邻整数之间,则这两个整数是( )
A.3和4 B.2和3 C.1和2 D.0和1
6.已知和都是方程的解,则a和b的值是( )
A. B.
C. D.
7.已知点在过点且与y轴平行的直线上,则点P坐标为( )
A. B. C. D.
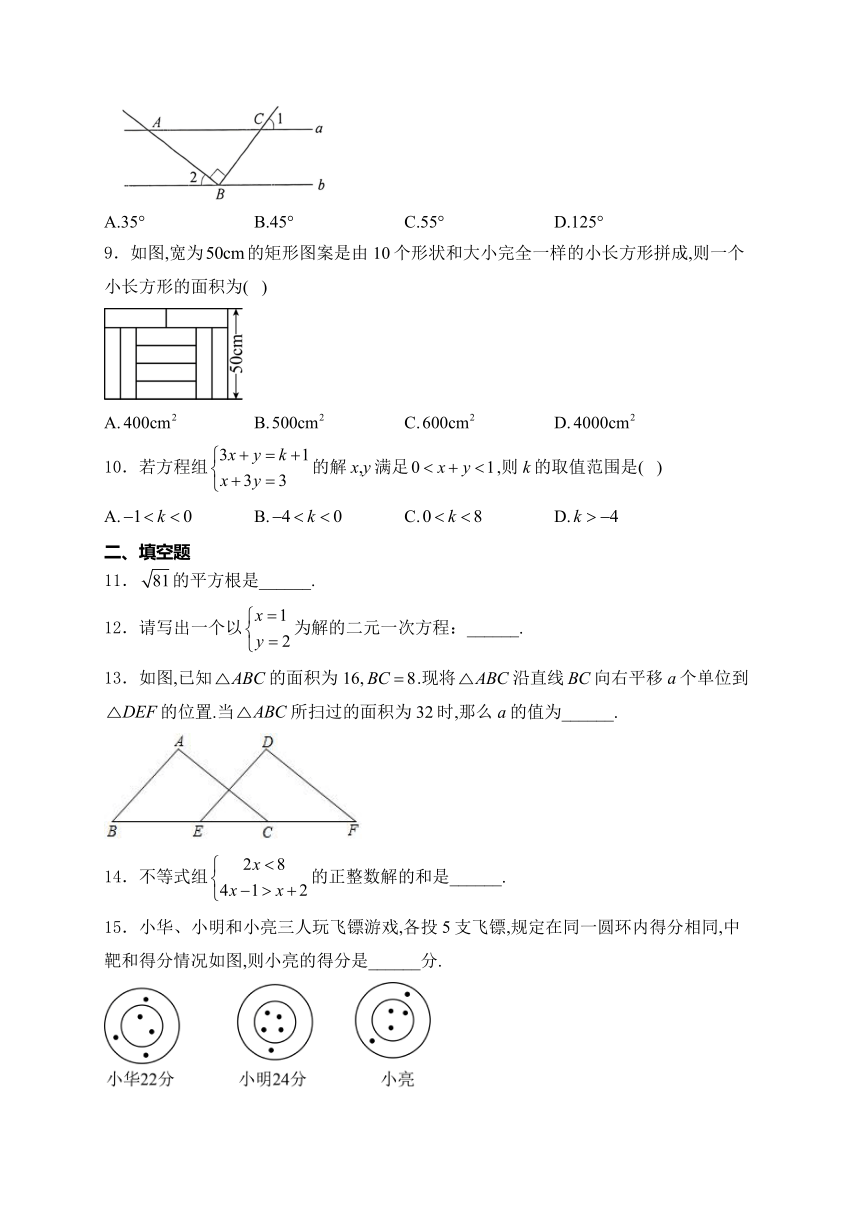
8.如图,直线,点B在直线b上,且,,则的度数为( )
A.35° B.45° C.55° D.125°
9.如图,宽为的矩形图案是由10个形状和大小完全一样的小长方形拼成,则一个小长方形的面积为( )
A. B. C. D.
10.若方程组的解x,y满足,则k的取值范围是( )
A. B. C. D.
二、填空题
11.的平方根是______.
12.请写出一个以为解的二元一次方程:______.
13.如图,已知的面积为16,.现将沿直线向右平移a个单位到的位置.当所扫过的面积为32时,那么a的值为______.
14.不等式组的正整数解的和是______.
15.小华、小明和小亮三人玩飞镖游戏,各投5支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小亮的得分是______分.
16.在平面直角坐标系中,对于点,我们把点叫做点P的伴随点.已知点的伴随点为,点的伴随点为,点的伴随点为,,这样依次得到点,,,,,.若点的坐标为,则点的坐标为______.
三、解答题
17.(1)计算:.
(2)解方程组:
(3)解不等式组:
18.根据题意结合图形填空:
如图,点E在上,点B在上,,.试证明:.
请将下面的证明过程补充完整.
证明:(已知)
且( )
(等量代换)
____________
( )
又(已知)
______(等量代换)
( ).
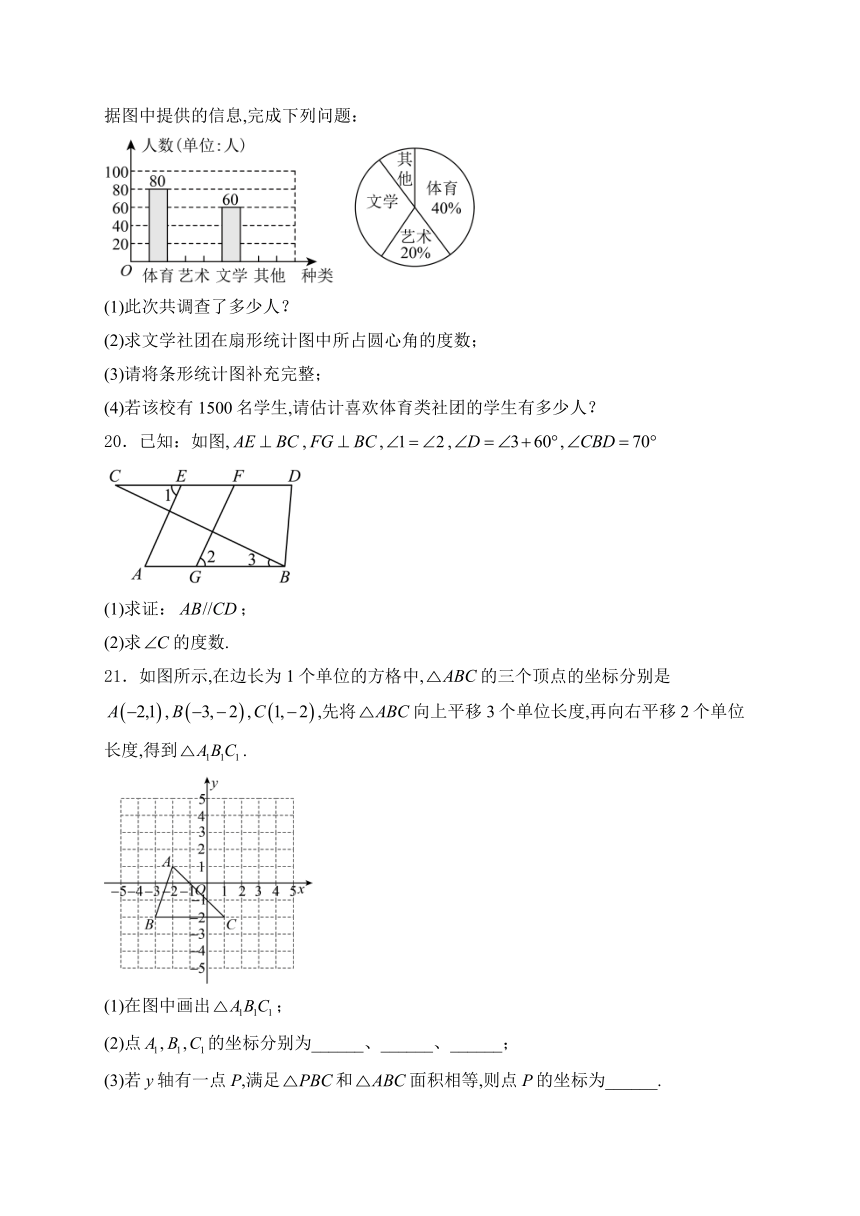
19.为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题:
(1)此次共调查了多少人?
(2)求文学社团在扇形统计图中所占圆心角的度数;
(3)请将条形统计图补充完整;
(4)若该校有1500名学生,请估计喜欢体育类社团的学生有多少人?
20.已知:如图,,,,,
(1)求证:;
(2)求的度数.
21.如图所示,在边长为1个单位的方格中,的三个顶点的坐标分别是,,,先将向上平移3个单位长度,再向右平移2个单位长度,得到.
(1)在图中画出;
(2)点,,的坐标分别为______、______、______;
(3)若y轴有一点P,满足和面积相等,则点P的坐标为______.
22.如图,在平面直角坐标系中,直线分别与x轴负半轴,y轴正半轴交于点,点,且a,b满足.
(1)求的面积;
(2)点P,T分别是线段,x轴正半轴上的动点,过点T作交y轴于点F,连接.若,请探究与之间的数量关系,(注:可用含n的式子表示)并说明理由.
23.阅读以下材料:
对于三个数a,b,c,用表示这三个数的平均数,用表示这三个数中最小的数.例如:;;
解决下列问题:
(1)填空:
如果,则x的取值范围为______.
(2)如果,求x.
24.今年义乌市准备争创全国卫生城市,某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
参考答案
1.答案:C
解析:A、了解《中国诗词大会》的收视率,调查范围广,适宜抽样调查,该选项不符合题意;
B、调查一批灯泡的使用寿命,具有破坏性且调查范围广,适宜抽样调查,该选项不符合题意;
C、了解七(1)班学生的身高情况,调查范围小,普查得到的调查结果比较准确,适合普查,该选项符合题意;
D、调查某品牌笔芯的使用寿命,具有破坏性且调查范围广,适宜抽样调查,该选项不符合题意;
故选:C.
2.答案:D
解析:A、1的立方根是1,故该选项不符合题意;
B、,4的平方根是,故该选项不符合题意;
C、负数有立方根,故该选项不符合题意;
D、9的算术平方根是3,该选项符合题意;
故选:D
3.答案:B
解析:A、相等的角不一定是对顶角,此项是假命题;
B、平行于同一条直线的两条直线互相平行,此项是真命题;
C、两直线平行,同旁内角互补,此项是假命题;
D、在同一平面内,垂直于同一条直线的两条直线互相平行,此项是假命题;
故选:B.
4.答案:D
解析:由数轴知,该不等式组解集的公共部分位于和3之间,且在端点是空心圆,不能取,在端点3是实心圆,可以取3,
该不等式组的解集为:.
故选:D.
5.答案:A
解析:,
,即,
这两个整数是3和4.
故选:A.
6.答案:B
解析:将和代入方程,
得,
解得.
故选B.
7.答案:C
解析:点在过点且与y轴平行的直线上,
的横坐标为2,
,解得,
.
故选:C.
8.答案:A
解析:∵,
∴BC与b所夹锐角等于,
又,
∴
故选:A.
9.答案:A
解析:设小长方形的宽为,长为,
根据题意得,,
解得,
一个小长方形的面积为.
故选:A.
10.答案:B
解析:∵,
观察方程组可知,上下两个方程相加可得:,
两边都除以4得,,
所以,
解得;
,
解得.
所以.
故选B.
11.答案:±3
解析:,
实数的平方根是.
故答案为:.
12.答案:(答案不唯一)
解析:∵二元一次方程的解为,
则方程可以为.
故答案是:(答案不唯一).
13.答案:4
解析:如图,连接AD,过点A作交BC于H.
∵,,
即,
∴,
∴
∴,
故答案为4.
14.答案:5
解析:
由,
得,
由,
得,解得,
不等式组的解集为,正整数解为2,3,
不等式组正整数解的和是5.
15.答案:23
解析:设投中圆环内的得分为x分,小圆内的得分为y分,
由题意得,,
解得,
小亮的得分是.
故答案为:23.
16.答案:
解析:点的坐标为,根据伴随点的定义得,
,,,,
依此类推,每4个点为一个循环组依次循环,
对于,m为正整数,有,,,,
,即当时,有
点的坐标为为.
故答案为:.
17.答案:(1)6
(2)
(3)
解析:(1)
.
(2)
由得,,
解得,
将代入得,,
解得,
原方程组的解为.
(3)
由式得,,
,
解得,
由式得,,
,
解得,
原不等式组的解集为.
18.答案:对顶角相等;,;两直线平行,同位角相等;;内错角相等,两直线平行
解析:证明:(已知)
且(对顶角相等)
(等量代换)
,
(两直线平行,同位角相等)
又(已知)
(等量代换)
(内错角相等,两直线平行).
19.答案:(1)200
(2)108°
(3)图见解析
(4)600
解析:(1)(人).
∴此次共调查200人.
(2).
∴文学社团在扇形统计图中所占圆心角的度数为108°.
(3)补全如图,
(4)(人).
∴估计该校喜欢体育类社团的学生有600人.
20.答案:(1)证明见解析
(2)
解析:(1)证明:∵,,
∴,
∴,
∵,
∴,
∴;
(2)∵,
∴,,
∵,,
∴,
∴,
∴.
21.答案:(1)图见解析
(2),,
(3)或
解析:(1)∵,,,
∴将向上平移3个单位长度,再向右平移2个单位长度得到,,,
∴如图所示,
(2)∵,,,
∴将向上平移3个单位长度,再向右平移2个单位长度得到,,,
故答案为,,;
(3)∵,,
∴,
∵,
∴,
∴,
设点,
∴,
∴,
∵和面积相等,
∴,
∴或,
∴或.
22.答案:(1)
(2),理由见解析
解析:(1),
又,,
,
解得,
,,
,,
.
(2)如图,延长交于H.
,
,
,,,,
,
,
又,
,
.
23.答案:(1)
(2)
解析:(1)由题意得:,
解得:.
故答案为:;
(2)依题意,.
∴,
即是2、、2x中最小的一个,
∴,
∴,
∴.
24.答案:(1)温馨提示牌和垃圾箱的单价各是50元和150元
(2)见解析
解析:(1)设温情提示牌的单价为x元,则垃圾箱的单价为3x元,
根据题意得,,
∴,
经检验,符合题意,
∴元,
即:温馨提示牌和垃圾箱的单价各是50元和150元;
(2)设购买温情提示牌y个(y为正整数),则垃圾箱为个,
根据题意得,意,
∴
∵y为正整数,
∴y为50,51,52,共3中方案;
有三种方案:①温馨提示牌50个,垃圾箱50个,
②温馨提示牌51个,垃圾箱49个,
②温馨提示牌52个,垃圾箱48个,
设总费用为w元
,
∵,∴w随y的增大而减小
∴当时,所需资金最少,最少是9800元.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列调查中,适合进行普查的是( )
A.了解《中国诗词大会》的收视率 B.调查一批灯泡的使用寿命
C.了解七(1)班学生的身高情况 D.调查某品牌笔芯的使用寿命
2.下列说法中,正确的是( )
A.1的立方根是 B.的平方根是2
C.负数没有立方根 D.9的算术平方根是3
3.在下列命题中,为真命题的是( )
A.相等的角是对顶角
B.平行于同一条直线的两条直线互相平行
C.同旁内角互补
D.垂直于同一条直线的两条直线互相垂直
4.一个一元一次不等式组的解集在数轴上表示如图所示,则该不等式组的解集为( )
A. B. C. D.
5.设,a在两个相邻整数之间,则这两个整数是( )
A.3和4 B.2和3 C.1和2 D.0和1
6.已知和都是方程的解,则a和b的值是( )
A. B.
C. D.
7.已知点在过点且与y轴平行的直线上,则点P坐标为( )
A. B. C. D.
8.如图,直线,点B在直线b上,且,,则的度数为( )
A.35° B.45° C.55° D.125°
9.如图,宽为的矩形图案是由10个形状和大小完全一样的小长方形拼成,则一个小长方形的面积为( )
A. B. C. D.
10.若方程组的解x,y满足,则k的取值范围是( )
A. B. C. D.
二、填空题
11.的平方根是______.
12.请写出一个以为解的二元一次方程:______.
13.如图,已知的面积为16,.现将沿直线向右平移a个单位到的位置.当所扫过的面积为32时,那么a的值为______.
14.不等式组的正整数解的和是______.
15.小华、小明和小亮三人玩飞镖游戏,各投5支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小亮的得分是______分.
16.在平面直角坐标系中,对于点,我们把点叫做点P的伴随点.已知点的伴随点为,点的伴随点为,点的伴随点为,,这样依次得到点,,,,,.若点的坐标为,则点的坐标为______.
三、解答题
17.(1)计算:.
(2)解方程组:
(3)解不等式组:
18.根据题意结合图形填空:
如图,点E在上,点B在上,,.试证明:.
请将下面的证明过程补充完整.
证明:(已知)
且( )
(等量代换)
____________
( )
又(已知)
______(等量代换)
( ).
19.为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题:
(1)此次共调查了多少人?
(2)求文学社团在扇形统计图中所占圆心角的度数;
(3)请将条形统计图补充完整;
(4)若该校有1500名学生,请估计喜欢体育类社团的学生有多少人?
20.已知:如图,,,,,
(1)求证:;
(2)求的度数.
21.如图所示,在边长为1个单位的方格中,的三个顶点的坐标分别是,,,先将向上平移3个单位长度,再向右平移2个单位长度,得到.
(1)在图中画出;
(2)点,,的坐标分别为______、______、______;
(3)若y轴有一点P,满足和面积相等,则点P的坐标为______.
22.如图,在平面直角坐标系中,直线分别与x轴负半轴,y轴正半轴交于点,点,且a,b满足.
(1)求的面积;
(2)点P,T分别是线段,x轴正半轴上的动点,过点T作交y轴于点F,连接.若,请探究与之间的数量关系,(注:可用含n的式子表示)并说明理由.
23.阅读以下材料:
对于三个数a,b,c,用表示这三个数的平均数,用表示这三个数中最小的数.例如:;;
解决下列问题:
(1)填空:
如果,则x的取值范围为______.
(2)如果,求x.
24.今年义乌市准备争创全国卫生城市,某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
参考答案
1.答案:C
解析:A、了解《中国诗词大会》的收视率,调查范围广,适宜抽样调查,该选项不符合题意;
B、调查一批灯泡的使用寿命,具有破坏性且调查范围广,适宜抽样调查,该选项不符合题意;
C、了解七(1)班学生的身高情况,调查范围小,普查得到的调查结果比较准确,适合普查,该选项符合题意;
D、调查某品牌笔芯的使用寿命,具有破坏性且调查范围广,适宜抽样调查,该选项不符合题意;
故选:C.
2.答案:D
解析:A、1的立方根是1,故该选项不符合题意;
B、,4的平方根是,故该选项不符合题意;
C、负数有立方根,故该选项不符合题意;
D、9的算术平方根是3,该选项符合题意;
故选:D
3.答案:B
解析:A、相等的角不一定是对顶角,此项是假命题;
B、平行于同一条直线的两条直线互相平行,此项是真命题;
C、两直线平行,同旁内角互补,此项是假命题;
D、在同一平面内,垂直于同一条直线的两条直线互相平行,此项是假命题;
故选:B.
4.答案:D
解析:由数轴知,该不等式组解集的公共部分位于和3之间,且在端点是空心圆,不能取,在端点3是实心圆,可以取3,
该不等式组的解集为:.
故选:D.
5.答案:A
解析:,
,即,
这两个整数是3和4.
故选:A.
6.答案:B
解析:将和代入方程,
得,
解得.
故选B.
7.答案:C
解析:点在过点且与y轴平行的直线上,
的横坐标为2,
,解得,
.
故选:C.
8.答案:A
解析:∵,
∴BC与b所夹锐角等于,
又,
∴
故选:A.
9.答案:A
解析:设小长方形的宽为,长为,
根据题意得,,
解得,
一个小长方形的面积为.
故选:A.
10.答案:B
解析:∵,
观察方程组可知,上下两个方程相加可得:,
两边都除以4得,,
所以,
解得;
,
解得.
所以.
故选B.
11.答案:±3
解析:,
实数的平方根是.
故答案为:.
12.答案:(答案不唯一)
解析:∵二元一次方程的解为,
则方程可以为.
故答案是:(答案不唯一).
13.答案:4
解析:如图,连接AD,过点A作交BC于H.
∵,,
即,
∴,
∴
∴,
故答案为4.
14.答案:5
解析:
由,
得,
由,
得,解得,
不等式组的解集为,正整数解为2,3,
不等式组正整数解的和是5.
15.答案:23
解析:设投中圆环内的得分为x分,小圆内的得分为y分,
由题意得,,
解得,
小亮的得分是.
故答案为:23.
16.答案:
解析:点的坐标为,根据伴随点的定义得,
,,,,
依此类推,每4个点为一个循环组依次循环,
对于,m为正整数,有,,,,
,即当时,有
点的坐标为为.
故答案为:.
17.答案:(1)6
(2)
(3)
解析:(1)
.
(2)
由得,,
解得,
将代入得,,
解得,
原方程组的解为.
(3)
由式得,,
,
解得,
由式得,,
,
解得,
原不等式组的解集为.
18.答案:对顶角相等;,;两直线平行,同位角相等;;内错角相等,两直线平行
解析:证明:(已知)
且(对顶角相等)
(等量代换)
,
(两直线平行,同位角相等)
又(已知)
(等量代换)
(内错角相等,两直线平行).
19.答案:(1)200
(2)108°
(3)图见解析
(4)600
解析:(1)(人).
∴此次共调查200人.
(2).
∴文学社团在扇形统计图中所占圆心角的度数为108°.
(3)补全如图,
(4)(人).
∴估计该校喜欢体育类社团的学生有600人.
20.答案:(1)证明见解析
(2)
解析:(1)证明:∵,,
∴,
∴,
∵,
∴,
∴;
(2)∵,
∴,,
∵,,
∴,
∴,
∴.
21.答案:(1)图见解析
(2),,
(3)或
解析:(1)∵,,,
∴将向上平移3个单位长度,再向右平移2个单位长度得到,,,
∴如图所示,
(2)∵,,,
∴将向上平移3个单位长度,再向右平移2个单位长度得到,,,
故答案为,,;
(3)∵,,
∴,
∵,
∴,
∴,
设点,
∴,
∴,
∵和面积相等,
∴,
∴或,
∴或.
22.答案:(1)
(2),理由见解析
解析:(1),
又,,
,
解得,
,,
,,
.
(2)如图,延长交于H.
,
,
,,,,
,
,
又,
,
.
23.答案:(1)
(2)
解析:(1)由题意得:,
解得:.
故答案为:;
(2)依题意,.
∴,
即是2、、2x中最小的一个,
∴,
∴,
∴.
24.答案:(1)温馨提示牌和垃圾箱的单价各是50元和150元
(2)见解析
解析:(1)设温情提示牌的单价为x元,则垃圾箱的单价为3x元,
根据题意得,,
∴,
经检验,符合题意,
∴元,
即:温馨提示牌和垃圾箱的单价各是50元和150元;
(2)设购买温情提示牌y个(y为正整数),则垃圾箱为个,
根据题意得,意,
∴
∵y为正整数,
∴y为50,51,52,共3中方案;
有三种方案:①温馨提示牌50个,垃圾箱50个,
②温馨提示牌51个,垃圾箱49个,
②温馨提示牌52个,垃圾箱48个,
设总费用为w元
,
∵,∴w随y的增大而减小
∴当时,所需资金最少,最少是9800元.
同课章节目录
