七年级数学上册5.2 数据的整理 导学案(知识清单 典型例题 巩固提升)
文档属性
| 名称 | 七年级数学上册5.2 数据的整理 导学案(知识清单 典型例题 巩固提升) |

|
|
| 格式 | docx | ||
| 文件大小 | 497.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-12 21:56:41 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
5.2 数据的整理 导学案
(一)学习目标:
1.学会整理简单的数据,并将数据制成表格.
2.回顾3种不同的统计图,知道统计图可以描述数据.
3.体会扇形统计图的基本特点,能计算扇形中各部分占总体的百分率.
(二)学习重难点:
重点:整理数据制作统计表与统计图.
难点:扇形中心角的计算.
阅读课本,识记知识:
把数据整理成统计表后,我们还可以用统计图来直观的表达整理的结果,我们学过的统计图有条形统计图、拆线统计图、扇形统计图。
统计表和统计图都是整理、表达和分析数字资料的重要工具统计图有条形统计图,拆线统计图,扇形统计图。
(1)扇形统计图反映的是各部分占总体的百分比
(2)在扇形统计图中:(1)圆代表总体; (2)扇形代表
总体中的一部分,若我们知道各部分扇形的中心角,则该部分占总体的百分率等于_中心角与周角之比 ;也可以用统计表中的数据计算各部分占总体的百分率.
(3)若我们知道该部分占总体的百分率,则这部分扇形中心角的度数=该部分占总体的百分率x 360
3.制作扇形统计图的步骤:
(1)先算出各部分数量占总数量的百分比;
(2)再算出各部分所对扇形的中心角度数;
(3)取适当的半径画圆, 在圆内画出各个扇形;
(4)在图中标出名称和所占的百分比
【例1】为了解学生心理健康情况,某学校在全校七、八、九三个年级共1000名学生中开展心理健康知识竞赛活动,根据竞赛成绩将各年级合格人数绘制了如图所示的统计表,则下列说法正确的是( )
各年级合格人数统计表
年级 七年级 八年级 九年级
合格人数(人) 337 330 322
A.七年级学生的合格率最高 B.九年级学生的合格人数最少
C.八年级学生的人数为330人 D.九年级学生的合格率为
【答案】B
【分析】本题考查统计应用,涉及百分比、合格率计算,读懂题意,结合选项逐项判断即可得到答案,掌握统计知识的应用是解决问题的关键.
【详解】解:由题意可知:
A、由于全校七、八、九三个年级共1000名学生中开展心理健康知识竞赛活动,无法计算七年级学生的合格率,该选项说法错误,不符合题意;
B、由表可知,九年级学生的合格人数最少,该选项说法正确,符合题意;
C、由于全校七、八、九三个年级共1000名学生中开展心理健康知识竞赛活动,无法计算八年级学生的人数,该选项说法错误,不符合题意;
D、由于全校七、八、九三个年级共1000名学生中开展心理健康知识竞赛活动,无法计算九年级学生的合格率,该选项说法错误,不符合题意;
故选:B.
【例2】 甲、乙两人的手机“微信运动”中2023年12月1日﹣7日的步数折线统计图如图所示,则根据统计图提供的信息,下列结论错误的是( )
A.1日﹣3日,甲的步数逐天增加
B.12月5日,甲、乙两人的步数相等
C.1日﹣4日,乙的步数逐天减少
D.4日﹣7日,乙的步数都少于甲的步数
【答案】D
【分析】本题主要考查了折线统计图,采用数形结合的思想解题,是解题的关键.直接根据折线统计图信息逐一判断即可得到答案.
【详解】由图象可得:
A.1日﹣3日,甲的步数逐天增加,故A说法正确,不符合题意;
B.12月5日,甲、乙两人的步数相等,故B说法正确,不符合题意;
C.1日﹣4日,乙的步数逐天减少,故C说法正确,不符合题意;
D.7日,乙的步数都大于甲的步数,故D说法错误,符合题意;
故选:D.
选择题
1.某校参加课外兴趣小组的学生人数统计图如图所示.若棋类小组有60人,则劳动实践小组的人数为( )
A.75 B.90 C.108 D.120
2.每年3月21日是世界睡眠日,良好的睡眠状况是保持身体健康的重要基础,为了解某校800名初三学生的睡眠时间,从13个班级中抽取50名学生进行调查,下列说法正确的是( )
A.800名学生是总体 B.50是样本容量
C.13个班级是抽取的一个样本 D.每名学生是个体
3.某果园为清楚地表示每种果树的棵数占总棵数的百分比,应绘制( )统计图。
A.条形 B.折线 C.扇形 D. 以上都不对
4.水产养殖中常采用“捉﹣﹣放﹣﹣捉”的方式估计一个鱼塘中鱼的数量,如从某个鱼塘中随机地捞出100条鱼,将这些鱼作上记号后再放回鱼塘,隔数日后再从该鱼塘随机捞出144条鱼,其中带有记号的有6条,从而估计该鱼塘有( )条鱼.
A.1600 B.2400 C.1800 D.2000
5.合肥市农科所在相同条件下经试验发现玉米种子的发芽率为,该市某种粮大户准备了玉米种子用来育种,他可能会损失大约( ).
A.971 B.129 C.1 D.29
6.进行数据的收集调查时,在明确调查问题、确定调查对象后一般还要完成以下4个步骤:①展开调查;②得出结论;③记录结果;④选择调查方法.但它们的顺序被打乱了,正确的顺序是 ( )
A.④①③② B.③④①② C.④③①② D.②④③①
7.榕榕对全班同学进行调查“你最喜欢的球类项目(只能选一项)”.然后依据所得数据绘制成扇形统计图.由图可知,在该班同学中,最受欢迎的球类项目是( )
A.羽毛球 B.乒乓球 C.排球 D.篮球
8.七(1)班同学根据兴趣分成四个小组,并制成了如图所示的条形图,若制成扇形图,则B组对应扇形的圆心角的度数为 ( )
A.60° B.90° C.120° D.135°
9.为了解西安市近9万名考生的数学成绩,教研部门从中抽取800名考生的数学成绩进行统计分析,下列说法正确的是( )
A.9万名考生是总体 B.每位考生的数学成绩是个体
C.800名考生是总体的一个样本 D.800名考生是样本容量
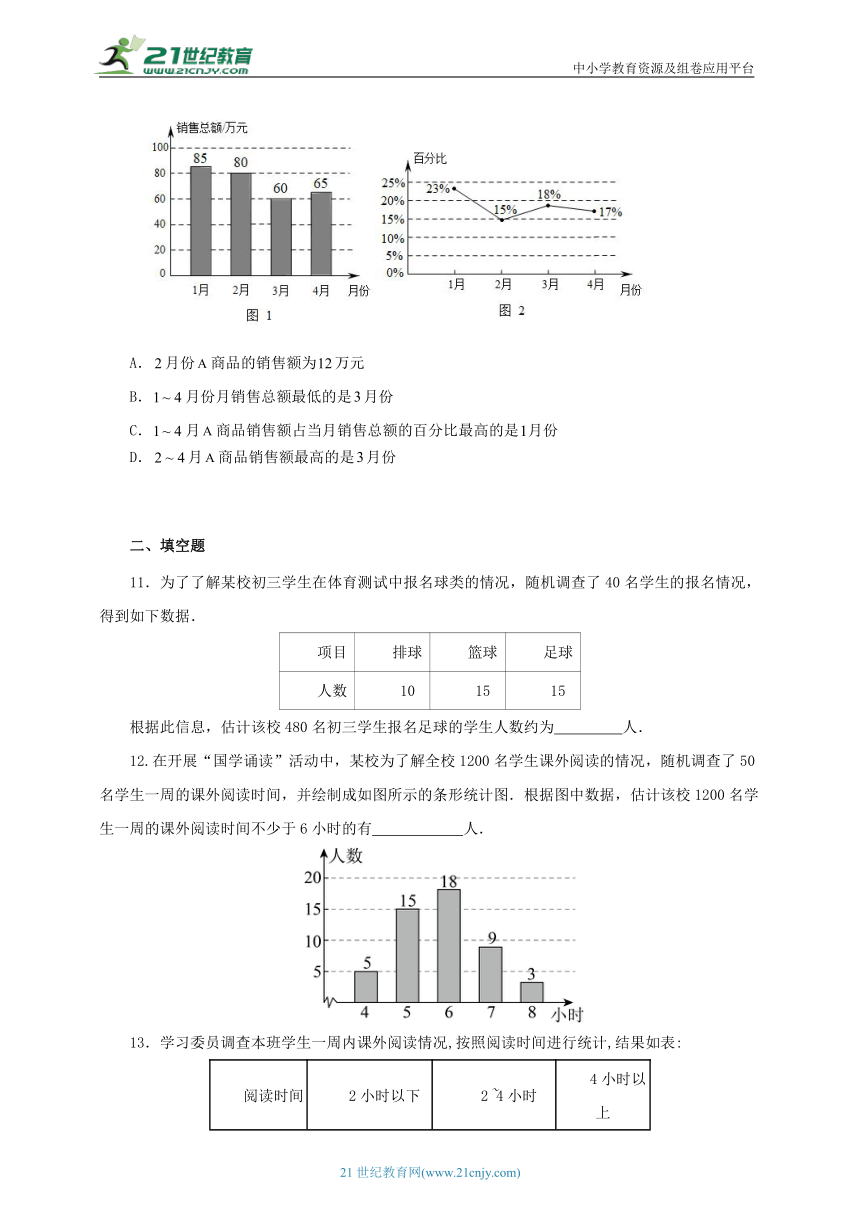
10.某商场年月份的月销售总额如图所示,其中商品的销售额占当月销售总额的百分比如图所示.根据图中信息,在以下四个结论中推断不合理的是( )
A.月份商品的销售额为万元
B.月份月销售总额最低的是月份
C.月商品销售额占当月销售总额的百分比最高的是月份
D.月商品销售额最高的是月份
填空题
11.为了了解某校初三学生在体育测试中报名球类的情况,随机调查了40名学生的报名情况,得到如下数据.
项目 排球 篮球 足球
人数 10 15 15
根据此信息,估计该校480名初三学生报名足球的学生人数约为 人.
12.在开展“国学诵读”活动中,某校为了解全校1200名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制成如图所示的条形统计图.根据图中数据,估计该校1200名学生一周的课外阅读时间不少于6小时的有 人.
13.学习委员调查本班学生一周内课外阅读情况,按照阅读时间进行统计,结果如表:
阅读时间 2小时以下 2~4小时 4小时以上
人数 20 16 a
百分比 b c 25%
则表中的a值为 .
14.小明同学发现自己解决问题时不细心,很容易造成失误,于是他想了一个办法,既能记录自己每天的失误次数,又能看出失误次数的变化情况,来提醒自己要细心做题,你认为他应该用 统计图来记录失误次数.
15.某厂生产了1000只灯泡.为了解这1000只灯泡的使用寿命,从中随机抽取了50只灯泡进行检测,获得了它们的使用寿命(单位:小时),数据整理如下:
使用寿命 x<1000 1000≤x<1600 1600≤x<2200 2200≤x<2800 x≥2800
灯泡只数 5 10 12 17 6
根据以上数据,估计这1000只灯泡中使用寿命不少于2200小时的灯泡的数量为 只.
三、解答题
16.两年前我市有县区申报了长寿之乡,并获认定.上月一所初中七(1)班学生社会实践前往该区一乡镇调研进入老龄化社会的数据.按国际通行标准,当一个国家或地区60及60岁以上人口达到总人口的10%,或65及65岁以上人口达到总人口的7%,这个区域进入老龄化社会.被调查的800人年龄情况统计图如下:
(1)这个乡镇是否进入老龄化社会?请说明理由.
(2)这个乡镇人口约20000人,求年龄不低于70岁的人数.
(3)请你为这个乡镇提一条合理化建议.
17.某校开展“阳光体育活动”,主要开设了以下四种运动项目:.乒乓球、.篮球、.跑步、.跳绳.为了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的条形统计图和扇形统计图.请你结合图中的信息解答下列问题:
(1)样本中喜欢项目的人数的百分比是 ,其所在扇形统计图中的扇形的圆心角度数是 ;
(2)把条形统计图补充完整;
(3)已知该校有人,根据样本估计全校喜欢乒乓球的人数是多少.
18.“荷式开门法”是荷兰的驾驶员开车门的一种方法,即开车门时总是用距车门较远的那只手开,从而减少视觉盲区,也就是左驾用右手开车门,右驾用左手开车门.这样上半身也惯性地转动.头部和肩膀也就自然转动.转动的过程中,眼睛首先会通过后视镜观察车后的情况,转身后眼睛也就自然而然地往外和往后看了.这个完整的动作就能更好地看到车后是否有行人或者行车了,进而避免很多不必要的事故.为推广这一做法,某公益团队在全市范围开展了专项宣传活动.在活动前和活动后分别随机抽取了部分市民,就执行“荷氏开门法”情况进行问卷调查,将收集的数据制成如下统计图表.
A:每次 B:经常 C:偶尔 D:从不
活动前执行“荷式开门法”情况统计表
类别 人数
A 68
B a●
C 510
D 177
合计 1000
活动后执行“荷式开门法”情况统计图
(1)“活动前执行‘荷氏开门法’情况统计表”中,B类别对应人数a不小心污损,请计算a的值;
(2)①为了更直现的反应A,B,C,D各类别所占的百分比,最适合的统计图是_______.(选填“扇形统计图”,“条形统计图”,“折线统计图”)
②宣传活动前,抽取的市民中哪一类别的人数占比最大?求其所在扇形对应圆心角的度数.
(3)若该区域有20万人,请估计活动前“从不”执行“荷氏开门法”总人数;
(4)小明认为,宣传活动后“从不”执行“荷氏开门法”的人数为178,比活动前增加了1人,因此公益组织开展的宣传活动没有效果.小明分析数据的方法是否合理?请说明理由.
(一)课后反思:
本节课我学会了:
本节课存在的问题:
把本节课所学知识画出思维导图
参考答案
1.【答案】B
【分析】本题主要考查了扇形统计图,用棋类的人数除以其占比即可得到总人数,再用总人数乘以劳动实践的人数占比即可得到答案.
【详解】解:人,
∴劳动实践小组的人数为90人,
故选B.
2.解:每年3月21日是世界睡眠日,良好的睡眠状况是保持身体健康的重要基础,为了解某校800名初三学生的睡眠时间,从13个班级中抽取50名学生进行调查,
A、800名学生的的睡眠状况是总体,故本选项不合题意;
B、50是样本容量,故本选项符合题意;
C、从13个班级中抽取50名学生的的睡眠状况是抽取的一个样本,故本选项不合题意;
D、每名学生的的睡眠状况是个体,故本选项不合题意;
故选:B.
3.【答案】C
【分析】本题考查了选择合适的统计图,此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答.
【详解】解:根据统计图的特点可知:某果园为清楚地表示每种果树的棵数占果树总棵数的百分比,应绘制扇形统计图.
故选:C.
4.解:设鱼塘中有x条鱼,
根据题意,得:=,
解得x=2400,
经检验x=2400是分式方程的解,
所以估计该鱼塘有2400条鱼,
故选:B.
5.【答案】D
【分析】本题考查用样本估计总体,蚕豆种子的发芽率为,可知不发芽率为,再乘以1000斤总数,即可知1000斤蚕豆种子中不能发芽的大约有多少.
【详解】解:黄石地区1000斤蚕豆种子中不能发芽的大约有斤,
即他可能会损失大约29斤,
故选:D.
【答案】A
【解析】略
7.【答案】D
【分析】本题考查的是扇形图的定义.利用扇形图可得喜欢各类项目的人数的百分比,选择同学们最喜欢的项目,即对应的百分比最大的,由此即可求出答案.
【详解】解:喜欢篮球项目的人所占的百分比最大,故该班最喜欢的球类项目是篮球.
故选:D.
8.【答案】D
【解析】略
9.【答案】B
【分析】本题考查了总体、个体、样本、样本容量,总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
【详解】解:A、9万名考生的数学成绩是总体,原说法错误,不符合题意;
B、每位考生的数学成绩是个体,原说法正确,符合题意;
C、800名考生的数学成绩是总体的一个样本,原说法错误,不符合题意;
D、800是样本.容量,原说法错误,不符合题意;
故选B.
10.【答案】D
【分析】本题考查了条形统计图、折线统计图,根据统计图中的数据,可以判断各个选项中的说法是否合理,从而可以解答本题,解答本题的关键是明确题意,利用数形结合的思想解答.
【详解】、由两个统计图可知月份的销售总额是万元,其中商品的销售额占,因此(万元),选项不符合题意;
、由条形统计图可知,月份月销售总额最低的是月份,因此选项不符合题意;
、从折线统计图可知,月商品销售额占当月销售总额的百分比最高的是月份,因此选项不符合题意;
、月份商品销售额为(万元),月份商品销售额为(万元),月份商品销售额为(万元),最高的是月份,因此选项符合题意,
故选:D.
11.解:估计该校480名初三学生报名足球的学生人数约为480×=180(人),
故答案为:180.
12. 【答案】720
【分析】本题考查了条形统计图的实际应用,属于简单题,会看统计图是解题关键.通过统计图求出课不少于6小时的人数占总人数的即可解题.
【详解】解:估计该校1200名学生一周的课外阅读时间不少于6小时的人数是(人).
故答案为:720.
13. 解:第(3)个问题不恰当,可改为“是否躺着看书”等与视力有关的问题.
14.【答案】折线
【分析】本题考查统计图的选择,解题的关键是掌握各类统计图的特点.条形统计图能很容易看出数量的多少,折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况,扇形统计图能反映部分与整体的关系;根据各类统计图的特点,结合题意即可得到答案.
【详解】解:根据统计图的特点可知:从统计图中既能记录自己每天的失误,又能看出失误的变化情况,应该用折线统计图.
故答案为:折线.
15.【答案】460
【分析】本题考查利用样本估计总体,用1000乘以抽查的灯泡中使用寿命不小于2200小时的灯泡所占的比例即可.
【详解】解:(只),
即这1000只灯泡中使用寿命不少于2200小时的灯泡的数量为460,
故答案为:460.
16.解:(1)60及60岁以上人口占的百分比是
(50+40+20)÷800
=13.75%;
65 及65 岁以上人口占的百分比是
(40+20)÷800
=7.5%;
60及60岁以上人口达到人口总数的13.75%,超过了10%.
65及65岁以上人口达到人口总数的7.5%,超过了7%.
∴该乡镇进入了老龄化社会;
(2)年龄不低于70岁的人数约为20000×=500(人);
(3)该乡镇进入了老龄化社会,可为老年人添置更多的锻炼设施.行政部门可为年轻人组织敬老孝亲专题活动。
17.【答案】(1),
(2)见解析
(3)根据样本估计全校喜欢乒乓球的人数是人
【分析】利用扇形统计图,用分别减去喜欢、、项目的百分比即可得到喜欢项目的人数的百分比,然后用这个百分比乘以得到项目在扇形统计图中的圆心角的度数;
先利用喜欢项目的人数和所占的百分比计算出所抽取的学生总数,再所抽取的学生总数乘以得到喜欢项目的人数,然后补全条形统计图;
用样本估计整体,用乘以样本中喜欢乒乓球的人数所占的百分比即可估计全校喜欢乒乓球的人数.
【详解】(1)解:,所在扇形统计图中的圆心角的度数是:;
故答案为:,;
(2)解:调查的总人数是:(人),
则喜欢的人数是:(人),
(3)解:全校喜欢乒乓球的人数是(人).
答:根据样本估计全校喜欢乒乓球的人数是人.
【点睛】本题考查了条形统计图:条形统计图是用线段长度表示数据,根据数量的多少画成长短不同的矩形直条,然后按顺序把这些直条排列起来从条形图可以很容易看出数据的大小,便于比较也考查了样本估计整体和扇形统计图.
18.【答案】(1)
(2)①扇形统计图 ②偶尔执行“荷式开门法”的人数最多;
(3)万人
(4)方法不合理,理由见解析
【分析】本题考查用样本估计总体,统计图的选择,关键是掌握用样本估计总体的方法,统计图的特点.
(1)用调查的总人数减去其他人数即可得到答案;
(2)①由统计图的特点,即可选择;②由扇形统计图的特点即可计算;
(3)用样本估计总体即可;
(4)求出宣传活动前后“从不”执行“荷氏开门法”的百分比,即可判断.
【详解】(1)解: (人),
∴的值为;
(2)①最适合的统计图是扇形统计图,
故答案为:扇形统计图;
②市民偶尔执行“荷式开门法”的人数最多,其所在扇形对应圆心角的度数;
(3)(万人)
∴估计该区域活动前“从不”执行“荷氏开门法”总人数是万人;
(4)小明分析数据的方法不合理,理由如下:宣传活动后“从不”执行“荷氏开门法”的百分比:,
宣传活动前“从不”执行“荷氏开门法”的百分比: 而宣传活动后下降到,因此公益组织开展的宣传活动有效果.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.2 数据的整理 导学案
(一)学习目标:
1.学会整理简单的数据,并将数据制成表格.
2.回顾3种不同的统计图,知道统计图可以描述数据.
3.体会扇形统计图的基本特点,能计算扇形中各部分占总体的百分率.
(二)学习重难点:
重点:整理数据制作统计表与统计图.
难点:扇形中心角的计算.
阅读课本,识记知识:
把数据整理成统计表后,我们还可以用统计图来直观的表达整理的结果,我们学过的统计图有条形统计图、拆线统计图、扇形统计图。
统计表和统计图都是整理、表达和分析数字资料的重要工具统计图有条形统计图,拆线统计图,扇形统计图。
(1)扇形统计图反映的是各部分占总体的百分比
(2)在扇形统计图中:(1)圆代表总体; (2)扇形代表
总体中的一部分,若我们知道各部分扇形的中心角,则该部分占总体的百分率等于_中心角与周角之比 ;也可以用统计表中的数据计算各部分占总体的百分率.
(3)若我们知道该部分占总体的百分率,则这部分扇形中心角的度数=该部分占总体的百分率x 360
3.制作扇形统计图的步骤:
(1)先算出各部分数量占总数量的百分比;
(2)再算出各部分所对扇形的中心角度数;
(3)取适当的半径画圆, 在圆内画出各个扇形;
(4)在图中标出名称和所占的百分比
【例1】为了解学生心理健康情况,某学校在全校七、八、九三个年级共1000名学生中开展心理健康知识竞赛活动,根据竞赛成绩将各年级合格人数绘制了如图所示的统计表,则下列说法正确的是( )
各年级合格人数统计表
年级 七年级 八年级 九年级
合格人数(人) 337 330 322
A.七年级学生的合格率最高 B.九年级学生的合格人数最少
C.八年级学生的人数为330人 D.九年级学生的合格率为
【答案】B
【分析】本题考查统计应用,涉及百分比、合格率计算,读懂题意,结合选项逐项判断即可得到答案,掌握统计知识的应用是解决问题的关键.
【详解】解:由题意可知:
A、由于全校七、八、九三个年级共1000名学生中开展心理健康知识竞赛活动,无法计算七年级学生的合格率,该选项说法错误,不符合题意;
B、由表可知,九年级学生的合格人数最少,该选项说法正确,符合题意;
C、由于全校七、八、九三个年级共1000名学生中开展心理健康知识竞赛活动,无法计算八年级学生的人数,该选项说法错误,不符合题意;
D、由于全校七、八、九三个年级共1000名学生中开展心理健康知识竞赛活动,无法计算九年级学生的合格率,该选项说法错误,不符合题意;
故选:B.
【例2】 甲、乙两人的手机“微信运动”中2023年12月1日﹣7日的步数折线统计图如图所示,则根据统计图提供的信息,下列结论错误的是( )
A.1日﹣3日,甲的步数逐天增加
B.12月5日,甲、乙两人的步数相等
C.1日﹣4日,乙的步数逐天减少
D.4日﹣7日,乙的步数都少于甲的步数
【答案】D
【分析】本题主要考查了折线统计图,采用数形结合的思想解题,是解题的关键.直接根据折线统计图信息逐一判断即可得到答案.
【详解】由图象可得:
A.1日﹣3日,甲的步数逐天增加,故A说法正确,不符合题意;
B.12月5日,甲、乙两人的步数相等,故B说法正确,不符合题意;
C.1日﹣4日,乙的步数逐天减少,故C说法正确,不符合题意;
D.7日,乙的步数都大于甲的步数,故D说法错误,符合题意;
故选:D.
选择题
1.某校参加课外兴趣小组的学生人数统计图如图所示.若棋类小组有60人,则劳动实践小组的人数为( )
A.75 B.90 C.108 D.120
2.每年3月21日是世界睡眠日,良好的睡眠状况是保持身体健康的重要基础,为了解某校800名初三学生的睡眠时间,从13个班级中抽取50名学生进行调查,下列说法正确的是( )
A.800名学生是总体 B.50是样本容量
C.13个班级是抽取的一个样本 D.每名学生是个体
3.某果园为清楚地表示每种果树的棵数占总棵数的百分比,应绘制( )统计图。
A.条形 B.折线 C.扇形 D. 以上都不对
4.水产养殖中常采用“捉﹣﹣放﹣﹣捉”的方式估计一个鱼塘中鱼的数量,如从某个鱼塘中随机地捞出100条鱼,将这些鱼作上记号后再放回鱼塘,隔数日后再从该鱼塘随机捞出144条鱼,其中带有记号的有6条,从而估计该鱼塘有( )条鱼.
A.1600 B.2400 C.1800 D.2000
5.合肥市农科所在相同条件下经试验发现玉米种子的发芽率为,该市某种粮大户准备了玉米种子用来育种,他可能会损失大约( ).
A.971 B.129 C.1 D.29
6.进行数据的收集调查时,在明确调查问题、确定调查对象后一般还要完成以下4个步骤:①展开调查;②得出结论;③记录结果;④选择调查方法.但它们的顺序被打乱了,正确的顺序是 ( )
A.④①③② B.③④①② C.④③①② D.②④③①
7.榕榕对全班同学进行调查“你最喜欢的球类项目(只能选一项)”.然后依据所得数据绘制成扇形统计图.由图可知,在该班同学中,最受欢迎的球类项目是( )
A.羽毛球 B.乒乓球 C.排球 D.篮球
8.七(1)班同学根据兴趣分成四个小组,并制成了如图所示的条形图,若制成扇形图,则B组对应扇形的圆心角的度数为 ( )
A.60° B.90° C.120° D.135°
9.为了解西安市近9万名考生的数学成绩,教研部门从中抽取800名考生的数学成绩进行统计分析,下列说法正确的是( )
A.9万名考生是总体 B.每位考生的数学成绩是个体
C.800名考生是总体的一个样本 D.800名考生是样本容量
10.某商场年月份的月销售总额如图所示,其中商品的销售额占当月销售总额的百分比如图所示.根据图中信息,在以下四个结论中推断不合理的是( )
A.月份商品的销售额为万元
B.月份月销售总额最低的是月份
C.月商品销售额占当月销售总额的百分比最高的是月份
D.月商品销售额最高的是月份
填空题
11.为了了解某校初三学生在体育测试中报名球类的情况,随机调查了40名学生的报名情况,得到如下数据.
项目 排球 篮球 足球
人数 10 15 15
根据此信息,估计该校480名初三学生报名足球的学生人数约为 人.
12.在开展“国学诵读”活动中,某校为了解全校1200名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制成如图所示的条形统计图.根据图中数据,估计该校1200名学生一周的课外阅读时间不少于6小时的有 人.
13.学习委员调查本班学生一周内课外阅读情况,按照阅读时间进行统计,结果如表:
阅读时间 2小时以下 2~4小时 4小时以上
人数 20 16 a
百分比 b c 25%
则表中的a值为 .
14.小明同学发现自己解决问题时不细心,很容易造成失误,于是他想了一个办法,既能记录自己每天的失误次数,又能看出失误次数的变化情况,来提醒自己要细心做题,你认为他应该用 统计图来记录失误次数.
15.某厂生产了1000只灯泡.为了解这1000只灯泡的使用寿命,从中随机抽取了50只灯泡进行检测,获得了它们的使用寿命(单位:小时),数据整理如下:
使用寿命 x<1000 1000≤x<1600 1600≤x<2200 2200≤x<2800 x≥2800
灯泡只数 5 10 12 17 6
根据以上数据,估计这1000只灯泡中使用寿命不少于2200小时的灯泡的数量为 只.
三、解答题
16.两年前我市有县区申报了长寿之乡,并获认定.上月一所初中七(1)班学生社会实践前往该区一乡镇调研进入老龄化社会的数据.按国际通行标准,当一个国家或地区60及60岁以上人口达到总人口的10%,或65及65岁以上人口达到总人口的7%,这个区域进入老龄化社会.被调查的800人年龄情况统计图如下:
(1)这个乡镇是否进入老龄化社会?请说明理由.
(2)这个乡镇人口约20000人,求年龄不低于70岁的人数.
(3)请你为这个乡镇提一条合理化建议.
17.某校开展“阳光体育活动”,主要开设了以下四种运动项目:.乒乓球、.篮球、.跑步、.跳绳.为了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的条形统计图和扇形统计图.请你结合图中的信息解答下列问题:
(1)样本中喜欢项目的人数的百分比是 ,其所在扇形统计图中的扇形的圆心角度数是 ;
(2)把条形统计图补充完整;
(3)已知该校有人,根据样本估计全校喜欢乒乓球的人数是多少.
18.“荷式开门法”是荷兰的驾驶员开车门的一种方法,即开车门时总是用距车门较远的那只手开,从而减少视觉盲区,也就是左驾用右手开车门,右驾用左手开车门.这样上半身也惯性地转动.头部和肩膀也就自然转动.转动的过程中,眼睛首先会通过后视镜观察车后的情况,转身后眼睛也就自然而然地往外和往后看了.这个完整的动作就能更好地看到车后是否有行人或者行车了,进而避免很多不必要的事故.为推广这一做法,某公益团队在全市范围开展了专项宣传活动.在活动前和活动后分别随机抽取了部分市民,就执行“荷氏开门法”情况进行问卷调查,将收集的数据制成如下统计图表.
A:每次 B:经常 C:偶尔 D:从不
活动前执行“荷式开门法”情况统计表
类别 人数
A 68
B a●
C 510
D 177
合计 1000
活动后执行“荷式开门法”情况统计图
(1)“活动前执行‘荷氏开门法’情况统计表”中,B类别对应人数a不小心污损,请计算a的值;
(2)①为了更直现的反应A,B,C,D各类别所占的百分比,最适合的统计图是_______.(选填“扇形统计图”,“条形统计图”,“折线统计图”)
②宣传活动前,抽取的市民中哪一类别的人数占比最大?求其所在扇形对应圆心角的度数.
(3)若该区域有20万人,请估计活动前“从不”执行“荷氏开门法”总人数;
(4)小明认为,宣传活动后“从不”执行“荷氏开门法”的人数为178,比活动前增加了1人,因此公益组织开展的宣传活动没有效果.小明分析数据的方法是否合理?请说明理由.
(一)课后反思:
本节课我学会了:
本节课存在的问题:
把本节课所学知识画出思维导图
参考答案
1.【答案】B
【分析】本题主要考查了扇形统计图,用棋类的人数除以其占比即可得到总人数,再用总人数乘以劳动实践的人数占比即可得到答案.
【详解】解:人,
∴劳动实践小组的人数为90人,
故选B.
2.解:每年3月21日是世界睡眠日,良好的睡眠状况是保持身体健康的重要基础,为了解某校800名初三学生的睡眠时间,从13个班级中抽取50名学生进行调查,
A、800名学生的的睡眠状况是总体,故本选项不合题意;
B、50是样本容量,故本选项符合题意;
C、从13个班级中抽取50名学生的的睡眠状况是抽取的一个样本,故本选项不合题意;
D、每名学生的的睡眠状况是个体,故本选项不合题意;
故选:B.
3.【答案】C
【分析】本题考查了选择合适的统计图,此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答.
【详解】解:根据统计图的特点可知:某果园为清楚地表示每种果树的棵数占果树总棵数的百分比,应绘制扇形统计图.
故选:C.
4.解:设鱼塘中有x条鱼,
根据题意,得:=,
解得x=2400,
经检验x=2400是分式方程的解,
所以估计该鱼塘有2400条鱼,
故选:B.
5.【答案】D
【分析】本题考查用样本估计总体,蚕豆种子的发芽率为,可知不发芽率为,再乘以1000斤总数,即可知1000斤蚕豆种子中不能发芽的大约有多少.
【详解】解:黄石地区1000斤蚕豆种子中不能发芽的大约有斤,
即他可能会损失大约29斤,
故选:D.
【答案】A
【解析】略
7.【答案】D
【分析】本题考查的是扇形图的定义.利用扇形图可得喜欢各类项目的人数的百分比,选择同学们最喜欢的项目,即对应的百分比最大的,由此即可求出答案.
【详解】解:喜欢篮球项目的人所占的百分比最大,故该班最喜欢的球类项目是篮球.
故选:D.
8.【答案】D
【解析】略
9.【答案】B
【分析】本题考查了总体、个体、样本、样本容量,总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
【详解】解:A、9万名考生的数学成绩是总体,原说法错误,不符合题意;
B、每位考生的数学成绩是个体,原说法正确,符合题意;
C、800名考生的数学成绩是总体的一个样本,原说法错误,不符合题意;
D、800是样本.容量,原说法错误,不符合题意;
故选B.
10.【答案】D
【分析】本题考查了条形统计图、折线统计图,根据统计图中的数据,可以判断各个选项中的说法是否合理,从而可以解答本题,解答本题的关键是明确题意,利用数形结合的思想解答.
【详解】、由两个统计图可知月份的销售总额是万元,其中商品的销售额占,因此(万元),选项不符合题意;
、由条形统计图可知,月份月销售总额最低的是月份,因此选项不符合题意;
、从折线统计图可知,月商品销售额占当月销售总额的百分比最高的是月份,因此选项不符合题意;
、月份商品销售额为(万元),月份商品销售额为(万元),月份商品销售额为(万元),最高的是月份,因此选项符合题意,
故选:D.
11.解:估计该校480名初三学生报名足球的学生人数约为480×=180(人),
故答案为:180.
12. 【答案】720
【分析】本题考查了条形统计图的实际应用,属于简单题,会看统计图是解题关键.通过统计图求出课不少于6小时的人数占总人数的即可解题.
【详解】解:估计该校1200名学生一周的课外阅读时间不少于6小时的人数是(人).
故答案为:720.
13. 解:第(3)个问题不恰当,可改为“是否躺着看书”等与视力有关的问题.
14.【答案】折线
【分析】本题考查统计图的选择,解题的关键是掌握各类统计图的特点.条形统计图能很容易看出数量的多少,折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况,扇形统计图能反映部分与整体的关系;根据各类统计图的特点,结合题意即可得到答案.
【详解】解:根据统计图的特点可知:从统计图中既能记录自己每天的失误,又能看出失误的变化情况,应该用折线统计图.
故答案为:折线.
15.【答案】460
【分析】本题考查利用样本估计总体,用1000乘以抽查的灯泡中使用寿命不小于2200小时的灯泡所占的比例即可.
【详解】解:(只),
即这1000只灯泡中使用寿命不少于2200小时的灯泡的数量为460,
故答案为:460.
16.解:(1)60及60岁以上人口占的百分比是
(50+40+20)÷800
=13.75%;
65 及65 岁以上人口占的百分比是
(40+20)÷800
=7.5%;
60及60岁以上人口达到人口总数的13.75%,超过了10%.
65及65岁以上人口达到人口总数的7.5%,超过了7%.
∴该乡镇进入了老龄化社会;
(2)年龄不低于70岁的人数约为20000×=500(人);
(3)该乡镇进入了老龄化社会,可为老年人添置更多的锻炼设施.行政部门可为年轻人组织敬老孝亲专题活动。
17.【答案】(1),
(2)见解析
(3)根据样本估计全校喜欢乒乓球的人数是人
【分析】利用扇形统计图,用分别减去喜欢、、项目的百分比即可得到喜欢项目的人数的百分比,然后用这个百分比乘以得到项目在扇形统计图中的圆心角的度数;
先利用喜欢项目的人数和所占的百分比计算出所抽取的学生总数,再所抽取的学生总数乘以得到喜欢项目的人数,然后补全条形统计图;
用样本估计整体,用乘以样本中喜欢乒乓球的人数所占的百分比即可估计全校喜欢乒乓球的人数.
【详解】(1)解:,所在扇形统计图中的圆心角的度数是:;
故答案为:,;
(2)解:调查的总人数是:(人),
则喜欢的人数是:(人),
(3)解:全校喜欢乒乓球的人数是(人).
答:根据样本估计全校喜欢乒乓球的人数是人.
【点睛】本题考查了条形统计图:条形统计图是用线段长度表示数据,根据数量的多少画成长短不同的矩形直条,然后按顺序把这些直条排列起来从条形图可以很容易看出数据的大小,便于比较也考查了样本估计整体和扇形统计图.
18.【答案】(1)
(2)①扇形统计图 ②偶尔执行“荷式开门法”的人数最多;
(3)万人
(4)方法不合理,理由见解析
【分析】本题考查用样本估计总体,统计图的选择,关键是掌握用样本估计总体的方法,统计图的特点.
(1)用调查的总人数减去其他人数即可得到答案;
(2)①由统计图的特点,即可选择;②由扇形统计图的特点即可计算;
(3)用样本估计总体即可;
(4)求出宣传活动前后“从不”执行“荷氏开门法”的百分比,即可判断.
【详解】(1)解: (人),
∴的值为;
(2)①最适合的统计图是扇形统计图,
故答案为:扇形统计图;
②市民偶尔执行“荷式开门法”的人数最多,其所在扇形对应圆心角的度数;
(3)(万人)
∴估计该区域活动前“从不”执行“荷氏开门法”总人数是万人;
(4)小明分析数据的方法不合理,理由如下:宣传活动后“从不”执行“荷氏开门法”的百分比:,
宣传活动前“从不”执行“荷氏开门法”的百分比: 而宣传活动后下降到,因此公益组织开展的宣传活动有效果.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
