【暑期预习衔接】第四单元多边形的面积(讲义)-2024-2025学年小学数学五年级上册北师大版(含答案)
文档属性
| 名称 | 【暑期预习衔接】第四单元多边形的面积(讲义)-2024-2025学年小学数学五年级上册北师大版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 222.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-13 00:00:00 | ||
图片预览




文档简介
第四单元多边形的面积
(知识梳理+专项练习)
分数乘法
正方形 正方形的面积=边长边长 S正 已知:正方形的面积,求边长
长方形 长方形的面积=长宽 S长=ab 已知:长方形的面积和长,求宽
平行四边形 平行四边形的面积=底高 S平=ah 已知:平行四边形的面积和底,求高 h=S平÷a
三角形 三角形的面积=底高÷2 S三=ah÷2 已知:三角形的面积和底,求高 H=S三X2÷a
梯形 梯形形的面积=(上底+下底)高÷2 S梯=(a+b)h÷2 已知:梯形的面积与上下底之和,求高 高=面积×2÷(上底+下底) 上底=面积×2÷高-下底
组合图形 当组合图形是凸出的,用两种或三种简单图形面积相加进行计算。 当组合图形是凹陷的,用一种最大的简单图形面积减较小的简单图形面积进行计算。
1、平行四边形面积公式推导:剪拼、平移
平行四边形可以转化成一个长方形;长方形的长相当于平行四边形的底; 长方形的宽相当于平行四边形的高;长方形的面积等于平行四边形的面积,因为长方形面积=长×宽,所以平行四边形面积=底×高。
2、三角形面积公式推导:旋转
两个完全一样的三角形可以拼成一个平行四边形,平行四边形的底相当于三角形的底;平行四边形的高相当于三角形的高;
平行四边形的面积等于三角形面积的2倍,因为平行四边形面积=底×高,所以三角形面积=底×高÷2
3、梯形面积公式推导:旋转
4、两个完全一样的梯形可以拼成一个平行四边形。平行四边形的底相当于梯形的上下底之和;平行四边形的高相当于梯形的高;平行四边形面积等于梯形面积的2倍,因为平行四边形面积=底×高,所以梯形面积=(上底+下底)×高÷2
5、等底等高的平行四边形面积相等;
等底等高的三角形面积相等;
等底等高的平行四边形面积是三角形面积的2倍。
6、长方形框架拉成平行四边形,周长不变,面积变小。
7、组合图形面积计算:必须转化成已学的简单图形。
当组合图形是凸出的,用虚线分割成几种简单图形,把简单图形面积相加计算。
当组合图形是凹陷的,用虚线补齐成一种最大的简单图形,用最大简单图形面积减几个较小的简单图形面积进行计算。
分数乘法
一、选择题
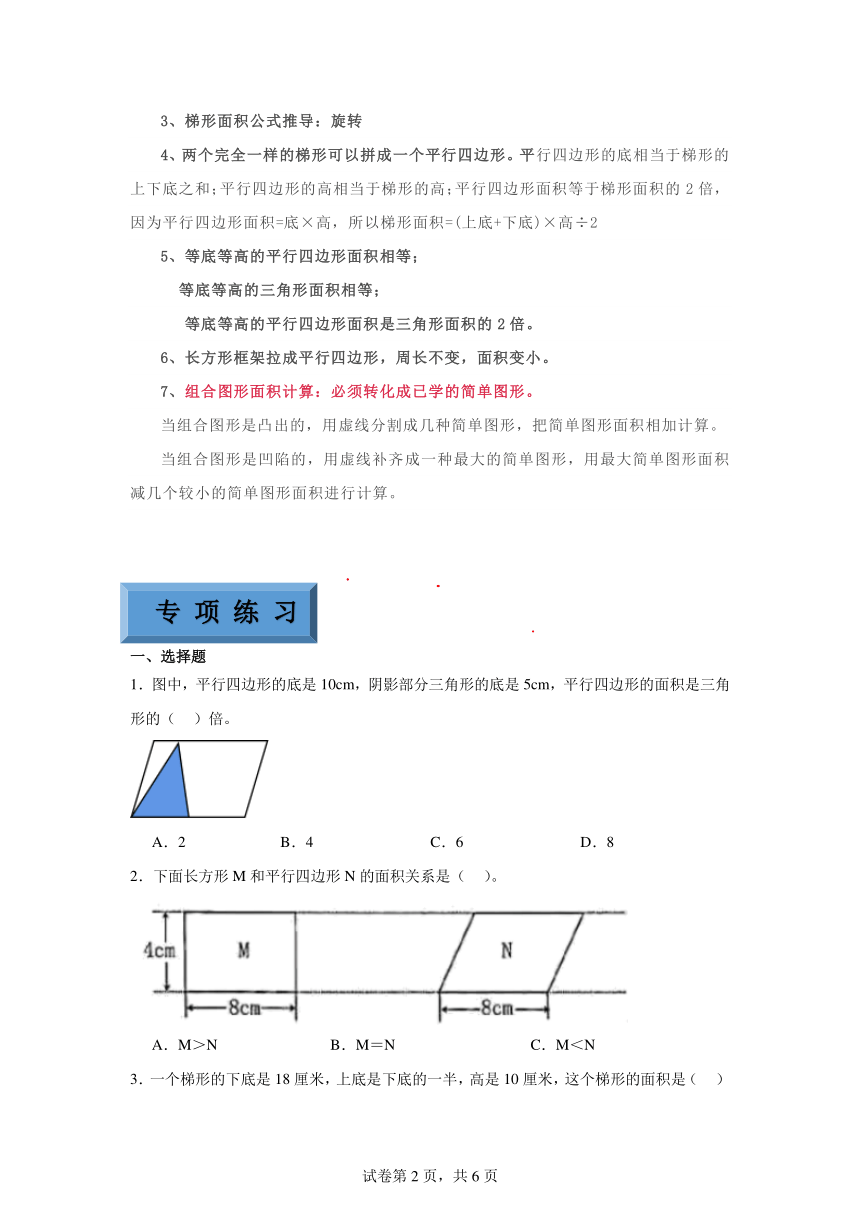
1.图中,平行四边形的底是10cm,阴影部分三角形的底是5cm,平行四边形的面积是三角形的( )倍。
A.2 B.4 C.6 D.8
2.下面长方形M和平行四边形N的面积关系是( )。
A.M>N B.M=N C.M<N
3.一个梯形的下底是18厘米,上底是下底的一半,高是10厘米,这个梯形的面积是( )平方厘米。
A.135 B.270 C.180
4.等底等高的两个平行四边形( )。
A.面积相等,形状也一定相同 B.面积相等,形状不一定相同 C.面积不一定相等
5.一个梯形的面积是80dm2,高是8dm,上底长6dm,下底长( )。
A.4dm B.10dm C.14dm D.20dm
6.把一个长方形框架拉“斜”成一个平行四边形,这个平行四边形和原长方形比( )
A.周长一样 B.面积一样
C.周长和面积都一样 D.不能确定
二、填空题
7.在综合实践活动课上,乐乐将一个长方形木框拉成一个平行四边形木框(如图所示),这个平行四边形的面积与原长方形面积相比,变( )(填“大”或“小”)了,平行四边形的面积是( )平方厘米。
8.一个平行四边形的面积是46平方米,一个三角形的面积与这个平行四边形的面积相等,这个三角形的底是8米,高是( )米。
9.一个梯形的面积是152m2,已知上底与下底的和是38m,高是( )m。
10.如图,梯形ABCD被它的一条对角线BD分成了两部分.△BDC的面积比△ABD的面积大10平方分米.已知梯形的下底与上底的长度之和是15分米,长度之差是5分米.则梯形ABCD的面积等于( )平方分米.
11.一张长方形的纸折成如图,恰好是边的中点,三角形的面积是,三角形的面积是,则长方形的面积是 ( ) .
12.一个底8分米,高7分米的三角形,它的面积是( )平方分米。与这个三角形等底等高的平行四边形的面积是( )平方分米。
13.一个底为12厘米,高为8厘米的三角形面积是( ),和它同底等高的平行四边形面积是( )。
14.一个直角梯形的上底是10分米,如果把上底延长4分米,就变成一个正方形,这个梯形的面积是( )平方分米.
15.一个直角三角形的两条直角边和斜边分别为3厘米、4厘米和5厘米,这个三角形斜边上的高是( )。
16.一堆钢管,截面堆成一个近似三角形,已知最上层有1根,最下层有4根,共堆了4层(相邻两层之间相差1根),这堆钢管共有( )根.
17.一个三角形的面积是24平方米,底是6米,高是( )米.和这个三角形等底等高的平行四边形的面积是( ).
18.一个平行四边形的面积是156平方米,底是12米,高是( ).
三、判断题
19.一个三角形的面积是20平方厘米,底是10厘米,那么它的高是4厘米。( )
20.面积相等的两个直角梯形一定能拼成一个长方形。 ( )
21.平行四边形割补成长方形后,面积不变,周长也不变。( )
22.等底等面积的平行四边形和三角形,三角形的高是平行四边形的2倍 ( )
23.平行四边形的对边之间和梯形两底之间的距离是它们的高,所以它们都有无数条高.( )
24.形状变了,周长、面积不变。( )
四、作图题
25.在下面格子图中,分别画一个三角形和一个平行四边形,使它们的面积都与图中梯形的面积相等。(每格表示1平方厘米的正方形)
五、解答题
26.一个直角三角形的面积是360平方厘米,一条直角边长是30厘米,另一条直角边长是多少厘米?
学校要在一个底为6米,高为2.4米的三角形花坛中栽花,如果每平方米能栽12株,这个花坛一共可以栽多少株?
在城固县南沙湖风景区入口处有一个上底为24m、下底为37m、高为16m的梯形宣传栏。宣传栏中间留出一个宽为1m,长为16m的长方形刷黄色油漆,其余的刷白色油漆。刷白色油漆的面积是多少m2?
老师拿来一张长0.6米、宽40厘米的红纸,用来剪一些两条直角边长都是4厘米的三角形小红旗,这张红纸最多可以剪多少面小红旗?
30.在下面的方格上画一个梯形,高是5cm,上底4cm,下底是6cm,并求出这个梯形的面积?(每个正方格边长是1cm)
31.在方格纸上画一个梯形,上底是4cm,下底是7cm,高是5cm,这个梯形的面积是多少平方厘米?(每个小方格的边长表示1cm)
一块三角形红领巾的底是10分米,高3.3分米,它的面积是多少平方分米?
33.我们经常见到圆木、钢管、砖块等堆成像下图的形状。列式计算图中砖块的总块数。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
2.B
【分析】由图可知:长方形的长是8厘米,宽是4厘米;平行四边形的底是8厘米,与之对应的高是4厘米。分别带入长方形、平行四边形面积公式求出面积,再比较即可。
【详解】长方形:8×4=32(平方厘米)
平行四边形:8×4=32(平方厘米)
32平方厘米=32平方厘米
所以长方形M和平行四边形N的面积相等。
故答案为:B
【点睛】本题主要考查平行四边形的面积公式。
3.A
【分析】由题意知,梯形的下底是18厘米,上底是下底的一半,高是10厘米,先求出上底的长,再根据梯形的面积=(上底+下底)×高÷2解答即可。
【详解】(18÷2+18)×10÷2
=27×10÷2
=135(平方厘米)
故答案为:A
【点睛】本题主要考查了学生对梯形面积公式的灵活应用。
4.B
【分析】平行四边形的面积=底×高,则底和高都相等的平行四边形面积一定相等,但平行四边形的底和高并不能确定平行四边形的形状,画图说明即可。
【详解】如图:
等底等高的两个平行四边形,面积相等,但形状不一定相同。
故答案为:B
5.C
【分析】设梯形的下底为x,将已知数据分别代入梯形的面积公式,S=(a+b)h÷2,即可求解。
【详解】解:设梯形的下底为xdm,
(6+x)×8÷2=80
(6+x)×8÷2×2=80×2
(6+x)×8=160
(6+x)×8÷8=160÷8
6+x=20
6+x-6=20-6
x=14
它的下底是14dm。
故答案为:C
【点睛】此题主要考查梯形的面积的计算方法的灵活应用。
6.A
【详解】因为把一个长方形框架拉成一个平行四边形后,四条边的长度没变,则四条边的长度和不变,即它的周长不变;
它的底不变,但是高变短了,所以面积变小了.
故选A
7. 小 15
【分析】长方形的面积=长×宽,平行四边形的面积=底×高,根据题意,将长方形木框拉成平行四边形木框,平行四边形的底等于长方形的长,平行四边形的高小于长方形的宽,所以,拉成的平行四边形的面积小于长方形的面积。根据平行四边形的面积公式,代入数据即可算出平行四边形的面积。
【详解】(平方厘米)
由分析可知,这个平行四边形的面积与原长方形面积相比,变小了,平行四边形的面积是15平方厘米。
8.11.5
【分析】根据平行四边形的面积与三角形的面积相等,可知一个三角形的面积是46平方米,再根据三角形的面积公式求出三角形的高,据此解答。
【详解】46×2÷8
=92÷8
=11.5(米)
答:高是11.5米。
故答案为11.5.
9.8
【分析】根据梯形面积公式:面积=(上底+下底)×高÷2,高=面积×2÷(上底+下底),代入数据,即可解答。
【详解】152×2÷38
=304÷38
=8(m)
一个梯形的面积是152m2,已知上底与下底的和是38m,高是8m。
【点睛】熟练掌握和灵活运用梯形面积公式是解答本题的关键。
10.30
【详解】试题分析:如图,作AB的平行线DE.三角形BDE的面积与三角形ABD的面积相等,三角形DEC的面积就是三角形BDC与三角形ABD的面积差(10平方分米).从而,可求出梯形高(三角形DEC的高)是:2×10÷5="4" (分米),梯形面积是:15×4÷2="30" (平方分米).
解:如图,作AB的平行线DE,
15×(2×10÷5)÷2=30(平方分米);
答:梯形ABCD的面积等于30 平方分米;
故答案为30.
点评:解答此题的关键是认真分析题意,先求出梯形的高,然后根据梯形的面积计算公式,解答即可.
11.42cm2
【解析】略
12. 28 56
【分析】根据三角形面积=底×高÷2,平行四边形面积=底×高,列式计算即可。
【详解】8×7÷2=28(平方分米)
8×7=56(平方分米)
一个底8分米,高7分米的三角形,它的面积是28平方分米。与这个三角形等底等高的平行四边形的面积是56平方分米。
【点睛】关键是掌握并灵活运用三角形和平行四边形面积公式。
13. 48平方厘米 96平方厘米
【分析】根据三角形面积公式:面积=底×高÷2,代入数据,求出三角形面积;根据平行四边形面积公式:面积=底×高;等底等高的平行四边形面积是三角形面积的2倍,据此解答。
【详解】12×8÷2
=96÷2
=48(平方厘米)
48×2=96(平方厘米)
一个底为12厘米,高为8厘米的三角形面积是48平方厘米,和它同底等高的平行四边形面积是96平方厘米。
【点睛】解答本题的关键明确等底等高的平行四边形的面积是三角形面积的2倍。
14.168
【解析】略
15.2.4厘米
【分析】因为在直角三角形中,斜边最长,于是可以得出斜边的长度,进而依据三角形的面积公式即可求解。
【详解】3×4÷2×2÷5
=12÷5
=2.4(厘米)
这个三角形斜边上的高是2.4厘米。
【点睛】解答此题的主要依据是:在直角三角形中,斜边最长,以及三角形面积的计算方法。
16.10
【详解】试题分析:根据题意,最上层有1根,最下层有4根,相邻两层相差1根,这堆钢管的层数是(4﹣1+1)层,根据梯形的面积计算方法进行解答.
解:(1+4)×(4﹣1+1)÷2,
=5×4÷2,
=10(根);
答:这堆钢管一共有10根.
故答案为10.
点评:此题主要考查梯形的面积计算方法,能够根据梯形的面积计算方法解决有关的实际问题.
17.8、48平方米
【详解】试题分析:(1)根据三角形的面积公式S=ah÷2,知道h=2S÷a,把面积24平方米,底6米代入即可求出高;
(2)根据等底等高的平行四边形的面积是三角形的面积的2倍,用三角形的面积24平方米乘2就是平行四边形的面积.
解:(1)24×2÷6,
=48÷6,
=8(米),
(2)24×2=48(平方米),
答:三角形的高是8米;和这个三角形等底等高的平行四边形的面积是48平方米;
故答案为8、48平方米.
点评:本题主要是灵活利用三角形的面积公式S=ah÷2及等底等高的平行四边形的面积与三角形的面积的关系解决问题.
18.13米
【详解】平行四边形的面积=底×高,有高=平行四边形的面积÷底,代入数值可得解.
156÷12=13(米)
故答案为13米.
19.√
【分析】根据三角形的面积=底×高÷2可知:三角形的高=面积×2÷底,据此代入数据求出三角形的高并判断即可。
【详解】20×2÷10
=40÷10
=4(厘米)
故答案为:√
【点睛】掌握三角形的面积公式是解答本题的关键。
20.×
【分析】两个完全一样的直角梯形一定能拼成一个长方形,但面积相等的两个直角梯形不一定完全一样,不一定能拼成一个长方形,据此求解。
【详解】如:一个梯形的上底是2厘米,下底是6厘米,高是4厘米。
面积:
(2+6)×4÷2
=8×2
=16(平方厘米)
另一个梯形的上底是3厘米,下底是5厘米,高是4厘米。
面积:
(3+5)×4÷2
=8×2
=16(平方厘米)
面积相等,但形状不同,无法拼成一个长方形,原题说法错误。
故答案为:×
21.×
【分析】如下图所示,平行四边形割补成长方形后,左边的三角形补到了右边,因此面积不变。长方形的长等于平行四边形的底,长方形的宽小于平行四边形的斜边,因此周长变小。
【详解】平行四边形割补成长方形后,面积不变,周长变小。
故答案为:×
【点睛】根据面积和周长的意义进行分析解答,理解长方形的宽小于平行四边形的斜边,因此长方形的周长小于平行四边形的周长是解题的关键。
22.
【详解】略
23.√
【解析】略
24.×
【分析】根据长方形、平行四边形的周长、面积的意义,把长方形拉长平行四边形后,周长不变,长方形的宽边长平行四边形的斜边,由于平行四边形的高比斜边小,长方形的长是平行四边形的底,根据平行四边形的面积公式:底×高;长方形的面积公式:长×宽,由此即可知道面积变小,据此判断。
【详解】
根据分析可知,形状变了,周长不变,面积变小。
原题干说法错误。
故答案为:×
【点睛】本题考查的目的是理解掌握长方形、平行四边形的周长、面积的公式。
25.见详解
【分析】根据题意,图中阴影部分为梯形,梯形的面积=(上底+下底)×高÷2,所以梯形的面积为(3+5)×2÷2=8,根据平行四边形的面积=底×高,三角形的面积=底×高÷2,确定各个图形的边长或底、高,然后再进行作图即可得到答案。
【详解】梯形的面积为
(3+5)×2÷2
=8×2÷2
=16÷2
=8
所以三角形的底可以是4,高是4;
平行四边形的底可以是4,高是2;
画图如下:
【点睛】解答此题的关键是熟练掌握平行四边形、三角形、梯形的面积公式,然后再确定各个图形的边长或底、高,最后进行作图即可。
26.24厘米
【分析】根据直角三角形面积:S=ab÷2,则b=2S÷a,代入数值计算即可。
【详解】360×2÷30
=720÷30
=24(厘米)
答:另一条直角边长是24厘米。
【点睛】本题考查直角三角形面积公式的应用,牢记直角三角形面积可用两条直角边的乘积除以2得到。
27.86株
【详解】试题分析:先求出三角形花坛的面积,再乘每平方米能栽的株数,就是共可栽的株数.据此解答.
解:6×2.4÷2×12,
=7.2×12,
=86.4,
≈86(株);
答:这个花坛一共可以栽86株.
点评:本题的关键是先求出三角形花坛的面积,注意得数要取近似值.
28.472m2
【分析】根据题意可知,刷白色油漆的面积等于梯形的面积减去中间长方形的面积,根据梯形的面积公式:S=(a+b)h÷2,长方形的面积公式:S=ab,把数据代入公式解答。
【详解】(24+37)×16÷2-16×1
=61×16÷2-16
=488-16
=472(m2)
答:刷白色油漆的面积是472m2。
【点睛】此题主要考查梯形、长方形面积公式的灵活运用,关键是熟记公式。
29.300面
【分析】两个直角边都是4厘米的直角三角形,可以拼成一个边长是4厘米的正方形;用除法分别求出长方形的长、宽里各包含多少4厘米,再根据长方形面积公式:面积=长×宽;代入数据,求出最多可以剪几个边长是4厘米的正方形,再乘2,即可求出最多可以剪多少面小红旗。
【详解】40厘米=0.4米;4厘米=0.04米
0.6÷0.04=15(个)
0.4÷0.04=10(个)
15×10=150(个)
150×2=300(面)
答:这张纸最多可以剪300面小红旗。
【点睛】本题考查平面图形的剪切问题,分别求出长方形长、宽最多能剪几个正方形,再利用长方形面积公式求出正方形的个数是解题的关键;注意单位名数的统一。
30.;
25cm2
【详解】(4+6)×5÷2=25(cm2)
31.图见详解;27.5平方厘米
【分析】根据题目要求画一个上底是4cm,下底是7cm,高是5cm的梯形,根据梯形的面积=(上底+下底)×高÷2,代入数据计算即可。
【详解】作图如下:
(4+7)×5÷2
=55÷2
=27.5(平方厘米)
答:这个梯形的面积是27.5平方厘米。
【点睛】此题考查了梯形的画法,以及梯形的面积计算。牢记公式认真计算即可。
32.16.5平方分米
【详解】试题分析:三角形的面积=底×高÷2,红领巾的底和高已知,代入公式即可求出这块红领巾的面积.
解:10×3.3÷2,
=33÷2,
=16.5(平方分米);
答:它的面积是16.5平方分米.
点评:此题主要考查三角形面积公式的应用.
33.20块
【分析】根据图示,近似梯形,利用堆成梯形的物品的计算方法:块数=(上层块数+下层块数)×层数÷2,代入数据求出砖块的总块数,据此解答。
【详解】(2+6)×5÷2
=8×5÷2
=40÷2
=20(块)
答:图中砖块有20块。
【点睛】本题的关键是根据堆成梯形物品的计算方法求出砖块的总块数。
答案第1页,共2页
答案第1页,共2页
(知识梳理+专项练习)
分数乘法
正方形 正方形的面积=边长边长 S正 已知:正方形的面积,求边长
长方形 长方形的面积=长宽 S长=ab 已知:长方形的面积和长,求宽
平行四边形 平行四边形的面积=底高 S平=ah 已知:平行四边形的面积和底,求高 h=S平÷a
三角形 三角形的面积=底高÷2 S三=ah÷2 已知:三角形的面积和底,求高 H=S三X2÷a
梯形 梯形形的面积=(上底+下底)高÷2 S梯=(a+b)h÷2 已知:梯形的面积与上下底之和,求高 高=面积×2÷(上底+下底) 上底=面积×2÷高-下底
组合图形 当组合图形是凸出的,用两种或三种简单图形面积相加进行计算。 当组合图形是凹陷的,用一种最大的简单图形面积减较小的简单图形面积进行计算。
1、平行四边形面积公式推导:剪拼、平移
平行四边形可以转化成一个长方形;长方形的长相当于平行四边形的底; 长方形的宽相当于平行四边形的高;长方形的面积等于平行四边形的面积,因为长方形面积=长×宽,所以平行四边形面积=底×高。
2、三角形面积公式推导:旋转
两个完全一样的三角形可以拼成一个平行四边形,平行四边形的底相当于三角形的底;平行四边形的高相当于三角形的高;
平行四边形的面积等于三角形面积的2倍,因为平行四边形面积=底×高,所以三角形面积=底×高÷2
3、梯形面积公式推导:旋转
4、两个完全一样的梯形可以拼成一个平行四边形。平行四边形的底相当于梯形的上下底之和;平行四边形的高相当于梯形的高;平行四边形面积等于梯形面积的2倍,因为平行四边形面积=底×高,所以梯形面积=(上底+下底)×高÷2
5、等底等高的平行四边形面积相等;
等底等高的三角形面积相等;
等底等高的平行四边形面积是三角形面积的2倍。
6、长方形框架拉成平行四边形,周长不变,面积变小。
7、组合图形面积计算:必须转化成已学的简单图形。
当组合图形是凸出的,用虚线分割成几种简单图形,把简单图形面积相加计算。
当组合图形是凹陷的,用虚线补齐成一种最大的简单图形,用最大简单图形面积减几个较小的简单图形面积进行计算。
分数乘法
一、选择题
1.图中,平行四边形的底是10cm,阴影部分三角形的底是5cm,平行四边形的面积是三角形的( )倍。
A.2 B.4 C.6 D.8
2.下面长方形M和平行四边形N的面积关系是( )。
A.M>N B.M=N C.M<N
3.一个梯形的下底是18厘米,上底是下底的一半,高是10厘米,这个梯形的面积是( )平方厘米。
A.135 B.270 C.180
4.等底等高的两个平行四边形( )。
A.面积相等,形状也一定相同 B.面积相等,形状不一定相同 C.面积不一定相等
5.一个梯形的面积是80dm2,高是8dm,上底长6dm,下底长( )。
A.4dm B.10dm C.14dm D.20dm
6.把一个长方形框架拉“斜”成一个平行四边形,这个平行四边形和原长方形比( )
A.周长一样 B.面积一样
C.周长和面积都一样 D.不能确定
二、填空题
7.在综合实践活动课上,乐乐将一个长方形木框拉成一个平行四边形木框(如图所示),这个平行四边形的面积与原长方形面积相比,变( )(填“大”或“小”)了,平行四边形的面积是( )平方厘米。
8.一个平行四边形的面积是46平方米,一个三角形的面积与这个平行四边形的面积相等,这个三角形的底是8米,高是( )米。
9.一个梯形的面积是152m2,已知上底与下底的和是38m,高是( )m。
10.如图,梯形ABCD被它的一条对角线BD分成了两部分.△BDC的面积比△ABD的面积大10平方分米.已知梯形的下底与上底的长度之和是15分米,长度之差是5分米.则梯形ABCD的面积等于( )平方分米.
11.一张长方形的纸折成如图,恰好是边的中点,三角形的面积是,三角形的面积是,则长方形的面积是 ( ) .
12.一个底8分米,高7分米的三角形,它的面积是( )平方分米。与这个三角形等底等高的平行四边形的面积是( )平方分米。
13.一个底为12厘米,高为8厘米的三角形面积是( ),和它同底等高的平行四边形面积是( )。
14.一个直角梯形的上底是10分米,如果把上底延长4分米,就变成一个正方形,这个梯形的面积是( )平方分米.
15.一个直角三角形的两条直角边和斜边分别为3厘米、4厘米和5厘米,这个三角形斜边上的高是( )。
16.一堆钢管,截面堆成一个近似三角形,已知最上层有1根,最下层有4根,共堆了4层(相邻两层之间相差1根),这堆钢管共有( )根.
17.一个三角形的面积是24平方米,底是6米,高是( )米.和这个三角形等底等高的平行四边形的面积是( ).
18.一个平行四边形的面积是156平方米,底是12米,高是( ).
三、判断题
19.一个三角形的面积是20平方厘米,底是10厘米,那么它的高是4厘米。( )
20.面积相等的两个直角梯形一定能拼成一个长方形。 ( )
21.平行四边形割补成长方形后,面积不变,周长也不变。( )
22.等底等面积的平行四边形和三角形,三角形的高是平行四边形的2倍 ( )
23.平行四边形的对边之间和梯形两底之间的距离是它们的高,所以它们都有无数条高.( )
24.形状变了,周长、面积不变。( )
四、作图题
25.在下面格子图中,分别画一个三角形和一个平行四边形,使它们的面积都与图中梯形的面积相等。(每格表示1平方厘米的正方形)
五、解答题
26.一个直角三角形的面积是360平方厘米,一条直角边长是30厘米,另一条直角边长是多少厘米?
学校要在一个底为6米,高为2.4米的三角形花坛中栽花,如果每平方米能栽12株,这个花坛一共可以栽多少株?
在城固县南沙湖风景区入口处有一个上底为24m、下底为37m、高为16m的梯形宣传栏。宣传栏中间留出一个宽为1m,长为16m的长方形刷黄色油漆,其余的刷白色油漆。刷白色油漆的面积是多少m2?
老师拿来一张长0.6米、宽40厘米的红纸,用来剪一些两条直角边长都是4厘米的三角形小红旗,这张红纸最多可以剪多少面小红旗?
30.在下面的方格上画一个梯形,高是5cm,上底4cm,下底是6cm,并求出这个梯形的面积?(每个正方格边长是1cm)
31.在方格纸上画一个梯形,上底是4cm,下底是7cm,高是5cm,这个梯形的面积是多少平方厘米?(每个小方格的边长表示1cm)
一块三角形红领巾的底是10分米,高3.3分米,它的面积是多少平方分米?
33.我们经常见到圆木、钢管、砖块等堆成像下图的形状。列式计算图中砖块的总块数。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
2.B
【分析】由图可知:长方形的长是8厘米,宽是4厘米;平行四边形的底是8厘米,与之对应的高是4厘米。分别带入长方形、平行四边形面积公式求出面积,再比较即可。
【详解】长方形:8×4=32(平方厘米)
平行四边形:8×4=32(平方厘米)
32平方厘米=32平方厘米
所以长方形M和平行四边形N的面积相等。
故答案为:B
【点睛】本题主要考查平行四边形的面积公式。
3.A
【分析】由题意知,梯形的下底是18厘米,上底是下底的一半,高是10厘米,先求出上底的长,再根据梯形的面积=(上底+下底)×高÷2解答即可。
【详解】(18÷2+18)×10÷2
=27×10÷2
=135(平方厘米)
故答案为:A
【点睛】本题主要考查了学生对梯形面积公式的灵活应用。
4.B
【分析】平行四边形的面积=底×高,则底和高都相等的平行四边形面积一定相等,但平行四边形的底和高并不能确定平行四边形的形状,画图说明即可。
【详解】如图:
等底等高的两个平行四边形,面积相等,但形状不一定相同。
故答案为:B
5.C
【分析】设梯形的下底为x,将已知数据分别代入梯形的面积公式,S=(a+b)h÷2,即可求解。
【详解】解:设梯形的下底为xdm,
(6+x)×8÷2=80
(6+x)×8÷2×2=80×2
(6+x)×8=160
(6+x)×8÷8=160÷8
6+x=20
6+x-6=20-6
x=14
它的下底是14dm。
故答案为:C
【点睛】此题主要考查梯形的面积的计算方法的灵活应用。
6.A
【详解】因为把一个长方形框架拉成一个平行四边形后,四条边的长度没变,则四条边的长度和不变,即它的周长不变;
它的底不变,但是高变短了,所以面积变小了.
故选A
7. 小 15
【分析】长方形的面积=长×宽,平行四边形的面积=底×高,根据题意,将长方形木框拉成平行四边形木框,平行四边形的底等于长方形的长,平行四边形的高小于长方形的宽,所以,拉成的平行四边形的面积小于长方形的面积。根据平行四边形的面积公式,代入数据即可算出平行四边形的面积。
【详解】(平方厘米)
由分析可知,这个平行四边形的面积与原长方形面积相比,变小了,平行四边形的面积是15平方厘米。
8.11.5
【分析】根据平行四边形的面积与三角形的面积相等,可知一个三角形的面积是46平方米,再根据三角形的面积公式求出三角形的高,据此解答。
【详解】46×2÷8
=92÷8
=11.5(米)
答:高是11.5米。
故答案为11.5.
9.8
【分析】根据梯形面积公式:面积=(上底+下底)×高÷2,高=面积×2÷(上底+下底),代入数据,即可解答。
【详解】152×2÷38
=304÷38
=8(m)
一个梯形的面积是152m2,已知上底与下底的和是38m,高是8m。
【点睛】熟练掌握和灵活运用梯形面积公式是解答本题的关键。
10.30
【详解】试题分析:如图,作AB的平行线DE.三角形BDE的面积与三角形ABD的面积相等,三角形DEC的面积就是三角形BDC与三角形ABD的面积差(10平方分米).从而,可求出梯形高(三角形DEC的高)是:2×10÷5="4" (分米),梯形面积是:15×4÷2="30" (平方分米).
解:如图,作AB的平行线DE,
15×(2×10÷5)÷2=30(平方分米);
答:梯形ABCD的面积等于30 平方分米;
故答案为30.
点评:解答此题的关键是认真分析题意,先求出梯形的高,然后根据梯形的面积计算公式,解答即可.
11.42cm2
【解析】略
12. 28 56
【分析】根据三角形面积=底×高÷2,平行四边形面积=底×高,列式计算即可。
【详解】8×7÷2=28(平方分米)
8×7=56(平方分米)
一个底8分米,高7分米的三角形,它的面积是28平方分米。与这个三角形等底等高的平行四边形的面积是56平方分米。
【点睛】关键是掌握并灵活运用三角形和平行四边形面积公式。
13. 48平方厘米 96平方厘米
【分析】根据三角形面积公式:面积=底×高÷2,代入数据,求出三角形面积;根据平行四边形面积公式:面积=底×高;等底等高的平行四边形面积是三角形面积的2倍,据此解答。
【详解】12×8÷2
=96÷2
=48(平方厘米)
48×2=96(平方厘米)
一个底为12厘米,高为8厘米的三角形面积是48平方厘米,和它同底等高的平行四边形面积是96平方厘米。
【点睛】解答本题的关键明确等底等高的平行四边形的面积是三角形面积的2倍。
14.168
【解析】略
15.2.4厘米
【分析】因为在直角三角形中,斜边最长,于是可以得出斜边的长度,进而依据三角形的面积公式即可求解。
【详解】3×4÷2×2÷5
=12÷5
=2.4(厘米)
这个三角形斜边上的高是2.4厘米。
【点睛】解答此题的主要依据是:在直角三角形中,斜边最长,以及三角形面积的计算方法。
16.10
【详解】试题分析:根据题意,最上层有1根,最下层有4根,相邻两层相差1根,这堆钢管的层数是(4﹣1+1)层,根据梯形的面积计算方法进行解答.
解:(1+4)×(4﹣1+1)÷2,
=5×4÷2,
=10(根);
答:这堆钢管一共有10根.
故答案为10.
点评:此题主要考查梯形的面积计算方法,能够根据梯形的面积计算方法解决有关的实际问题.
17.8、48平方米
【详解】试题分析:(1)根据三角形的面积公式S=ah÷2,知道h=2S÷a,把面积24平方米,底6米代入即可求出高;
(2)根据等底等高的平行四边形的面积是三角形的面积的2倍,用三角形的面积24平方米乘2就是平行四边形的面积.
解:(1)24×2÷6,
=48÷6,
=8(米),
(2)24×2=48(平方米),
答:三角形的高是8米;和这个三角形等底等高的平行四边形的面积是48平方米;
故答案为8、48平方米.
点评:本题主要是灵活利用三角形的面积公式S=ah÷2及等底等高的平行四边形的面积与三角形的面积的关系解决问题.
18.13米
【详解】平行四边形的面积=底×高,有高=平行四边形的面积÷底,代入数值可得解.
156÷12=13(米)
故答案为13米.
19.√
【分析】根据三角形的面积=底×高÷2可知:三角形的高=面积×2÷底,据此代入数据求出三角形的高并判断即可。
【详解】20×2÷10
=40÷10
=4(厘米)
故答案为:√
【点睛】掌握三角形的面积公式是解答本题的关键。
20.×
【分析】两个完全一样的直角梯形一定能拼成一个长方形,但面积相等的两个直角梯形不一定完全一样,不一定能拼成一个长方形,据此求解。
【详解】如:一个梯形的上底是2厘米,下底是6厘米,高是4厘米。
面积:
(2+6)×4÷2
=8×2
=16(平方厘米)
另一个梯形的上底是3厘米,下底是5厘米,高是4厘米。
面积:
(3+5)×4÷2
=8×2
=16(平方厘米)
面积相等,但形状不同,无法拼成一个长方形,原题说法错误。
故答案为:×
21.×
【分析】如下图所示,平行四边形割补成长方形后,左边的三角形补到了右边,因此面积不变。长方形的长等于平行四边形的底,长方形的宽小于平行四边形的斜边,因此周长变小。
【详解】平行四边形割补成长方形后,面积不变,周长变小。
故答案为:×
【点睛】根据面积和周长的意义进行分析解答,理解长方形的宽小于平行四边形的斜边,因此长方形的周长小于平行四边形的周长是解题的关键。
22.
【详解】略
23.√
【解析】略
24.×
【分析】根据长方形、平行四边形的周长、面积的意义,把长方形拉长平行四边形后,周长不变,长方形的宽边长平行四边形的斜边,由于平行四边形的高比斜边小,长方形的长是平行四边形的底,根据平行四边形的面积公式:底×高;长方形的面积公式:长×宽,由此即可知道面积变小,据此判断。
【详解】
根据分析可知,形状变了,周长不变,面积变小。
原题干说法错误。
故答案为:×
【点睛】本题考查的目的是理解掌握长方形、平行四边形的周长、面积的公式。
25.见详解
【分析】根据题意,图中阴影部分为梯形,梯形的面积=(上底+下底)×高÷2,所以梯形的面积为(3+5)×2÷2=8,根据平行四边形的面积=底×高,三角形的面积=底×高÷2,确定各个图形的边长或底、高,然后再进行作图即可得到答案。
【详解】梯形的面积为
(3+5)×2÷2
=8×2÷2
=16÷2
=8
所以三角形的底可以是4,高是4;
平行四边形的底可以是4,高是2;
画图如下:
【点睛】解答此题的关键是熟练掌握平行四边形、三角形、梯形的面积公式,然后再确定各个图形的边长或底、高,最后进行作图即可。
26.24厘米
【分析】根据直角三角形面积:S=ab÷2,则b=2S÷a,代入数值计算即可。
【详解】360×2÷30
=720÷30
=24(厘米)
答:另一条直角边长是24厘米。
【点睛】本题考查直角三角形面积公式的应用,牢记直角三角形面积可用两条直角边的乘积除以2得到。
27.86株
【详解】试题分析:先求出三角形花坛的面积,再乘每平方米能栽的株数,就是共可栽的株数.据此解答.
解:6×2.4÷2×12,
=7.2×12,
=86.4,
≈86(株);
答:这个花坛一共可以栽86株.
点评:本题的关键是先求出三角形花坛的面积,注意得数要取近似值.
28.472m2
【分析】根据题意可知,刷白色油漆的面积等于梯形的面积减去中间长方形的面积,根据梯形的面积公式:S=(a+b)h÷2,长方形的面积公式:S=ab,把数据代入公式解答。
【详解】(24+37)×16÷2-16×1
=61×16÷2-16
=488-16
=472(m2)
答:刷白色油漆的面积是472m2。
【点睛】此题主要考查梯形、长方形面积公式的灵活运用,关键是熟记公式。
29.300面
【分析】两个直角边都是4厘米的直角三角形,可以拼成一个边长是4厘米的正方形;用除法分别求出长方形的长、宽里各包含多少4厘米,再根据长方形面积公式:面积=长×宽;代入数据,求出最多可以剪几个边长是4厘米的正方形,再乘2,即可求出最多可以剪多少面小红旗。
【详解】40厘米=0.4米;4厘米=0.04米
0.6÷0.04=15(个)
0.4÷0.04=10(个)
15×10=150(个)
150×2=300(面)
答:这张纸最多可以剪300面小红旗。
【点睛】本题考查平面图形的剪切问题,分别求出长方形长、宽最多能剪几个正方形,再利用长方形面积公式求出正方形的个数是解题的关键;注意单位名数的统一。
30.;
25cm2
【详解】(4+6)×5÷2=25(cm2)
31.图见详解;27.5平方厘米
【分析】根据题目要求画一个上底是4cm,下底是7cm,高是5cm的梯形,根据梯形的面积=(上底+下底)×高÷2,代入数据计算即可。
【详解】作图如下:
(4+7)×5÷2
=55÷2
=27.5(平方厘米)
答:这个梯形的面积是27.5平方厘米。
【点睛】此题考查了梯形的画法,以及梯形的面积计算。牢记公式认真计算即可。
32.16.5平方分米
【详解】试题分析:三角形的面积=底×高÷2,红领巾的底和高已知,代入公式即可求出这块红领巾的面积.
解:10×3.3÷2,
=33÷2,
=16.5(平方分米);
答:它的面积是16.5平方分米.
点评:此题主要考查三角形面积公式的应用.
33.20块
【分析】根据图示,近似梯形,利用堆成梯形的物品的计算方法:块数=(上层块数+下层块数)×层数÷2,代入数据求出砖块的总块数,据此解答。
【详解】(2+6)×5÷2
=8×5÷2
=40÷2
=20(块)
答:图中砖块有20块。
【点睛】本题的关键是根据堆成梯形物品的计算方法求出砖块的总块数。
答案第1页,共2页
答案第1页,共2页
同课章节目录
