6.4 角 课件(共23张PPT) 2024-2025学年数学青岛版七年级上册
文档属性
| 名称 | 6.4 角 课件(共23张PPT) 2024-2025学年数学青岛版七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-13 13:51:12 | ||
图片预览




文档简介
(共23张PPT)
6.4 角
第6章 基本的几何图形
学习目标
1.理解角的概念,掌握角的表示方法.(重点)
2.会正确使用量角器,认识角的常用度量单位.
3.会进行度、分、秒的简单换算.
情境引入
你能不能从图中找到角?
情境引入
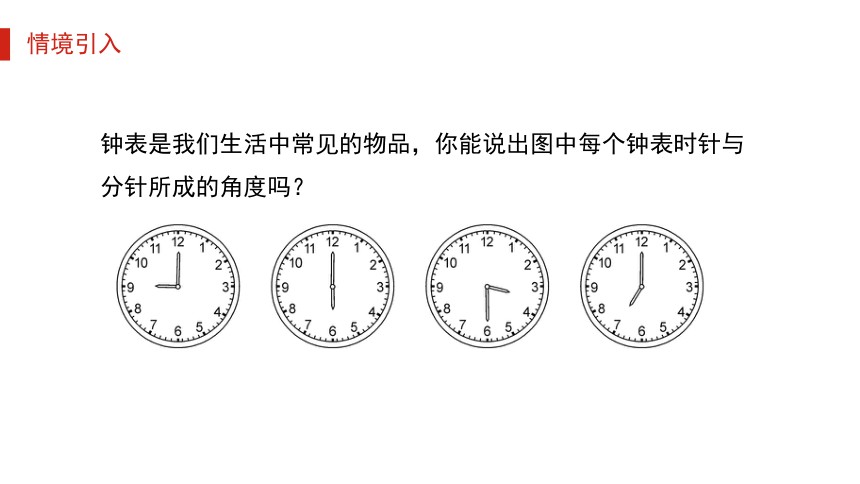
钟表是我们生活中常见的物品,你能说出图中每个钟表时针与分针所成的角度吗?
合作探究
知识点1 角的概念及表示方法
新课讲解
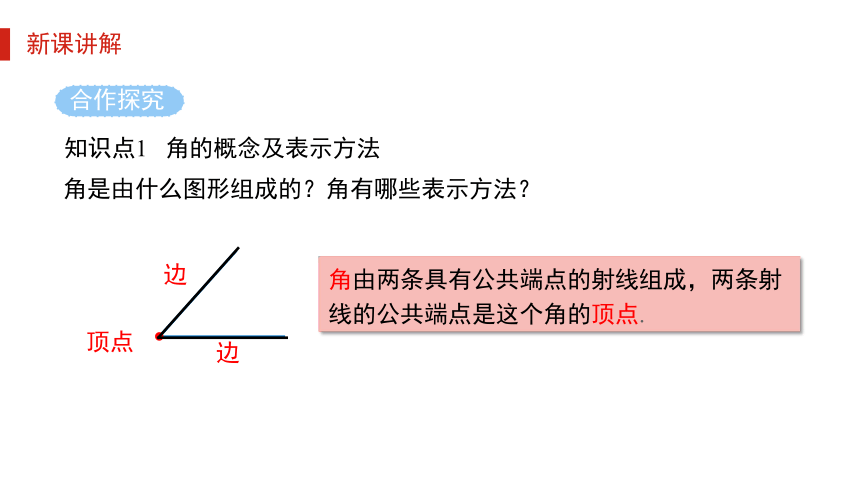
角由两条具有公共端点的射线组成,两条射线的公共端点是这个角的顶点.
顶点
边
边
角是由什么图形组成的?角有哪些表示方法?
新课讲解
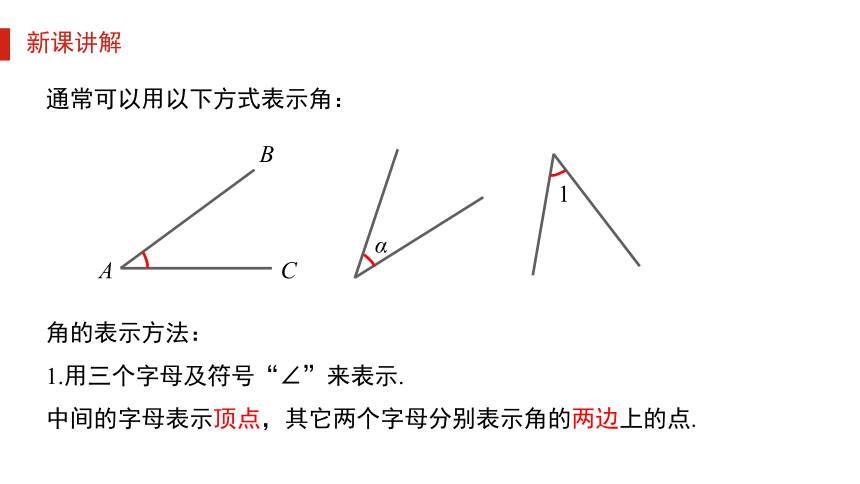
通常可以用以下方式表示角:
A
B
C
α
1
角的表示方法:
1.用三个字母及符号“∠”来表示.
中间的字母表示顶点,其它两个字母分别表示角的两边上的点.
新课讲解
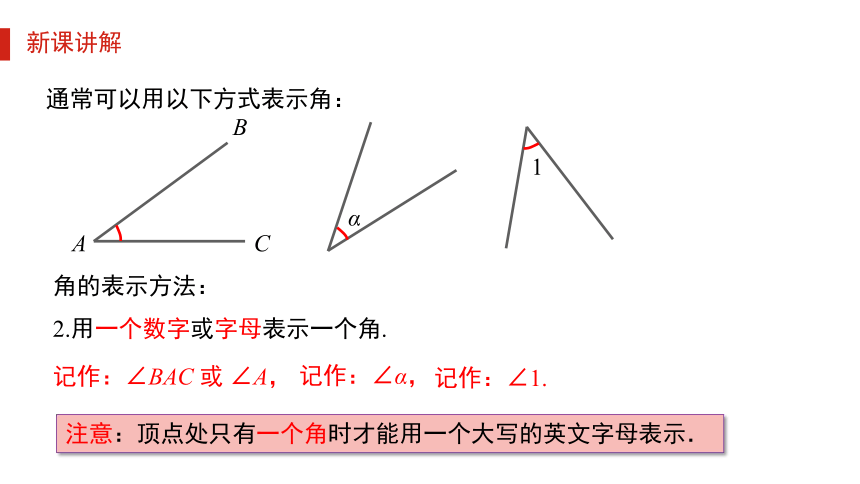
通常可以用以下方式表示角:
A
B
C
记作:∠BAC 或 ∠A,
记作:∠α,
记作:∠1.
α
1
注意:顶点处只有一个角时才能用一个大写的英文字母表示.
角的表示方法:
2.用一个数字或字母表示一个角.
新课讲解
典例分析
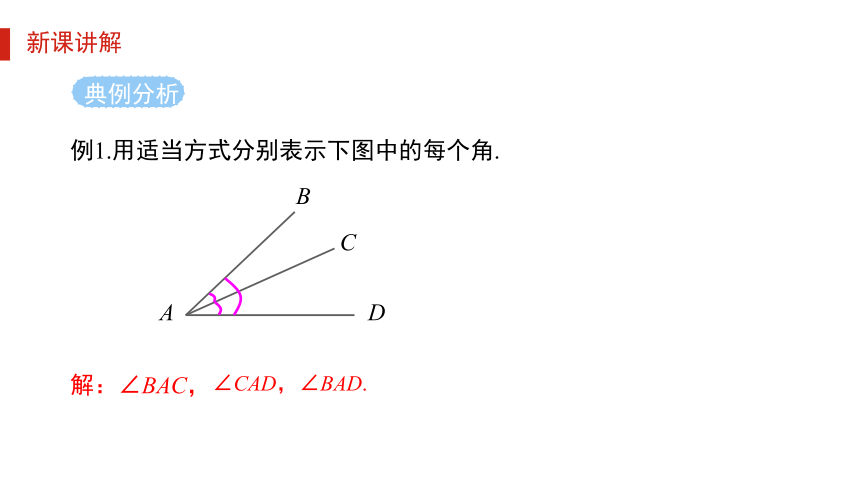
例1.用适当方式分别表示下图中的每个角.
A
D
B
C
解:∠BAC,
∠CAD,
∠BAD.
新课讲解
裁纸刀在开合过程中形成了大小不同的角.你还能举出其他类似的例子吗?
议一议
新课讲解
角也可以看成是由一条射线绕着它的端点旋转而成的.
O
始边
终边
新课讲解
一条射线绕它的端点旋转,当终边和始边成一条直线时,形成平角.
终边继续旋转,当它又和始边重合时,形成周角.
O
A
B
1 平角 = 180°
O
A
(B)
1 周角 = 360°
度,分,秒.
1°的60分之一为1分,记作“1′”,即1°=60′.
1′的60分之一为1秒,记作“1″”,即1′=60″.
量角器.
思考:怎么知道一个角的大小?
角的度量工具:
角的度量单位:
新课讲解
新课讲解
例2.计算:
(1)1.45°等于多少分?等于多少秒?
(2)1 800″ 等于多少分?等于多少度?
解:(1)60′×1.45 = 87′,60″×87 = 5 220″,
即 1.45°= 87′= 5 220″;
(2)′×1 800=30′,
()°×30=0.5°,
即 1 800″= 30′=0.5°.
典例分析
新课讲解
例3.计算下列各题:
(1)153°39′+25°40′38″;
(2)90°-37°24′38″;
解:(1)153°39′+25°40′38″=178°79′38″
=179°19′38″.
(2)90°-37°24′38″
=89°59′60″-37°24′38″=52°35′22″.
典例分析
新课讲解
例3.计算下列各题:
(3)25°53′28″×5;
(4)15°20′÷6.
解:(3)25°53′28″×5=25°×5+53′×5+28″×5
=125°+265′+140″=129°27′20″;
(4)15°20′÷6
=12°200′÷6=12°÷6+200′÷6
=2°+198′÷6+2′÷6
=2°+33′+120″÷6=2°33′20″.
典例分析
新课讲解
做一做
(1)请用字母表示图中的每个城市.
(2)请用字母分别表示以北京为中心的每两个城市之间的夹角.
A
B
C
D
.
.
.
.
.
O
典例分析
例4.小红早晨8:30出发,中午12:30到家,则小红出发时时针和分针的夹角为____,到家时时针和分针的夹角为______.
75°
165°
新课讲解
当堂小练
1.下列关于平角、周角的说法:①平角是一条直线;②周角是一条射线;③反向延长射线OA,就形成一个平角;④由一条射线绕其端点旋转,始边与终边重合而形成的图形叫周角.其中正确的是( )
A.①③
B.②④
C.①④
D.③④
D
2.计算:
(1)6 300″= 105 ′= 1.75 °;
(2)()°= 45 ′= 2 700 ″;
(3)57.27°= 57°16′12″ ;
(4)36°48′36″= 36.81 °.
105
1.75
45
2 700
57°16′12″
36.81
当堂小练
3.2022年3月23日15时40分,“天宫课堂”第二课在中国空间站开讲,神舟十三号乘组航天员翟志刚、王亚平、叶光富进行授课.当钟表在15时40分时,时针与分针所成的角的度数是 130° .
130°
当堂小练
4.魏老师去菜市场买菜,他发现若把5 kg的菜放到秤上,指针盘上的指针转了180°.
(1)如果把0.5 kg的菜放在秤上,求指针转过的角度;
(2)如果指针转了270°,这些菜有多少千克?
解:(1)×0.5=18°.
答:把0.5 kg的菜放在秤上,指针转过的角度是18°.
(2)270°÷=7.5(kg).
答:这些菜有7.5 kg.
当堂小练
课堂小结
1.角的组成及角的表示方法.
2.用量角器度量一个角.
3.度、分、秒单位间的换算.
6.4 角
第6章 基本的几何图形
学习目标
1.理解角的概念,掌握角的表示方法.(重点)
2.会正确使用量角器,认识角的常用度量单位.
3.会进行度、分、秒的简单换算.
情境引入
你能不能从图中找到角?
情境引入
钟表是我们生活中常见的物品,你能说出图中每个钟表时针与分针所成的角度吗?
合作探究
知识点1 角的概念及表示方法
新课讲解
角由两条具有公共端点的射线组成,两条射线的公共端点是这个角的顶点.
顶点
边
边
角是由什么图形组成的?角有哪些表示方法?
新课讲解
通常可以用以下方式表示角:
A
B
C
α
1
角的表示方法:
1.用三个字母及符号“∠”来表示.
中间的字母表示顶点,其它两个字母分别表示角的两边上的点.
新课讲解
通常可以用以下方式表示角:
A
B
C
记作:∠BAC 或 ∠A,
记作:∠α,
记作:∠1.
α
1
注意:顶点处只有一个角时才能用一个大写的英文字母表示.
角的表示方法:
2.用一个数字或字母表示一个角.
新课讲解
典例分析
例1.用适当方式分别表示下图中的每个角.
A
D
B
C
解:∠BAC,
∠CAD,
∠BAD.
新课讲解
裁纸刀在开合过程中形成了大小不同的角.你还能举出其他类似的例子吗?
议一议
新课讲解
角也可以看成是由一条射线绕着它的端点旋转而成的.
O
始边
终边
新课讲解
一条射线绕它的端点旋转,当终边和始边成一条直线时,形成平角.
终边继续旋转,当它又和始边重合时,形成周角.
O
A
B
1 平角 = 180°
O
A
(B)
1 周角 = 360°
度,分,秒.
1°的60分之一为1分,记作“1′”,即1°=60′.
1′的60分之一为1秒,记作“1″”,即1′=60″.
量角器.
思考:怎么知道一个角的大小?
角的度量工具:
角的度量单位:
新课讲解
新课讲解
例2.计算:
(1)1.45°等于多少分?等于多少秒?
(2)1 800″ 等于多少分?等于多少度?
解:(1)60′×1.45 = 87′,60″×87 = 5 220″,
即 1.45°= 87′= 5 220″;
(2)′×1 800=30′,
()°×30=0.5°,
即 1 800″= 30′=0.5°.
典例分析
新课讲解
例3.计算下列各题:
(1)153°39′+25°40′38″;
(2)90°-37°24′38″;
解:(1)153°39′+25°40′38″=178°79′38″
=179°19′38″.
(2)90°-37°24′38″
=89°59′60″-37°24′38″=52°35′22″.
典例分析
新课讲解
例3.计算下列各题:
(3)25°53′28″×5;
(4)15°20′÷6.
解:(3)25°53′28″×5=25°×5+53′×5+28″×5
=125°+265′+140″=129°27′20″;
(4)15°20′÷6
=12°200′÷6=12°÷6+200′÷6
=2°+198′÷6+2′÷6
=2°+33′+120″÷6=2°33′20″.
典例分析
新课讲解
做一做
(1)请用字母表示图中的每个城市.
(2)请用字母分别表示以北京为中心的每两个城市之间的夹角.
A
B
C
D
.
.
.
.
.
O
典例分析
例4.小红早晨8:30出发,中午12:30到家,则小红出发时时针和分针的夹角为____,到家时时针和分针的夹角为______.
75°
165°
新课讲解
当堂小练
1.下列关于平角、周角的说法:①平角是一条直线;②周角是一条射线;③反向延长射线OA,就形成一个平角;④由一条射线绕其端点旋转,始边与终边重合而形成的图形叫周角.其中正确的是( )
A.①③
B.②④
C.①④
D.③④
D
2.计算:
(1)6 300″= 105 ′= 1.75 °;
(2)()°= 45 ′= 2 700 ″;
(3)57.27°= 57°16′12″ ;
(4)36°48′36″= 36.81 °.
105
1.75
45
2 700
57°16′12″
36.81
当堂小练
3.2022年3月23日15时40分,“天宫课堂”第二课在中国空间站开讲,神舟十三号乘组航天员翟志刚、王亚平、叶光富进行授课.当钟表在15时40分时,时针与分针所成的角的度数是 130° .
130°
当堂小练
4.魏老师去菜市场买菜,他发现若把5 kg的菜放到秤上,指针盘上的指针转了180°.
(1)如果把0.5 kg的菜放在秤上,求指针转过的角度;
(2)如果指针转了270°,这些菜有多少千克?
解:(1)×0.5=18°.
答:把0.5 kg的菜放在秤上,指针转过的角度是18°.
(2)270°÷=7.5(kg).
答:这些菜有7.5 kg.
当堂小练
课堂小结
1.角的组成及角的表示方法.
2.用量角器度量一个角.
3.度、分、秒单位间的换算.
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
