人教版数学八年级上册11.1.2三角形的高线、中线与角平分线 精品同步练习(含解析)
文档属性
| 名称 | 人教版数学八年级上册11.1.2三角形的高线、中线与角平分线 精品同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-13 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版八年级上册数学 1.2三角形的高线、中线与角平分线 同步练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.下列各组图形中,AD是的高的图形是
A. B. C. D.
2.如图,用三角板作的边上的高线,下列三角板的摆放位置正确的是( )
A. B.C.D.
3.如图,△ABC中,D,E分别是BC上两点,且BD=DE=EC,则图中面积相等的三角形有( )
A.4对 B.5对 C.6对 D.7对
4.如图,在直角三角形ABC中,点B沿CB所在直线远离C点移动,下列说法错误的是( )
A.三角形面积随之增大 B.∠CAB的度数随之增大
C.BC边上的高随之增大 D.边AB的长度随之增大
5.已知BD是的中线,,且的周长为11,则的周长是( )
A.9 B.14 C.16 D.不能确定
6.下列说法正确的个数有( )
①三角形的高、中线、角平分线都是线段;
②三角形的三条角平分线都在三角形内部,且交于同一点;
③三角形的三条高都在三角形内部;
④三角形的一条中线把该三角形分成面积相等的两部分.
A.1个 B.2个 C.3个 D.4个
7.能把一个三角形的面积平均分成两个面积相等的三角形,这条线一定是这个三角形的一条( )
A.角平分线 B.高 C.中线 D.一条边的垂直平分线
8.下面四个图形中,线段是的高的是( )
A. B.
C. D.
9.如图所示,在中,与的平分线交于点,过点作交于点,交于点,那么下列结论:①;②;③和都是等腰三角形;④的周长等于与的和,其中正确的有( )
A.4个 B.3个 C.2个 D.1个
10.如图,在△ABC中,点M、N是∠ABC与∠ACB三等分线的交点.若∠A=60°,则∠BMN的度数为( )
A.45° B.50° C.60° D.65°
填空题(本大题共5小题,每小题4分,共20分。)
如图,在5×5的方格纸中,每个小正方形边长为1,点O、A、B在方格纸的交点(格点)上,在第四象限内的格点上找点C,使△ABC的面积为3,则这样的点C共有个_____个.
12.如图,已知△ABC,通过测量、计算得△ABC的面积约为____cm2.(结果保留一位小数)
13.任意一个三角形被一条中线分成两个三角形,则这两个三角形:①形状相同;②面积相等;③全等.上述说法中,正确的是________ .
14.如图,在△ABC中E是BC上的一点,BC=3BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=12,则S△ADF﹣S△BEF=____.
15.如图,△ABC的面积为1,分别倍长(延长一倍)AB,BC,CA得到△A1B1C1,再分别倍长A1B1,B1C1,C1A1得到△A2B2C2.…按此规律,倍长2020次后得到的△A2020B2020C2020的面积为_____.
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.如图,点,,都落在网格的格点上.
(1)写出点,,的坐标;
(2)求的面积:
(3)把先向左平移4个单位长度,再向下平移5个单位长度,得,画出.
17.已知的周长为,是边上的中线,.
(1)如图,当时,求的长.
(2)若,能否求出的长?为什么?
18.在中,交的延长线于点,点是线段上的一个动点.
特例研究:
当点与点重合时,过作交的延长线于点,如图①所示,通过观察﹑测量与的长度,得到.请给予证明.
猜想证明:
当点由点向点移动到如图②所示的位置时,过作交的延长线于点,过作交于点,此时请你通过观察,测量与的长度,猜想并写出与之间存在的数量关系,并证明你的猜想.
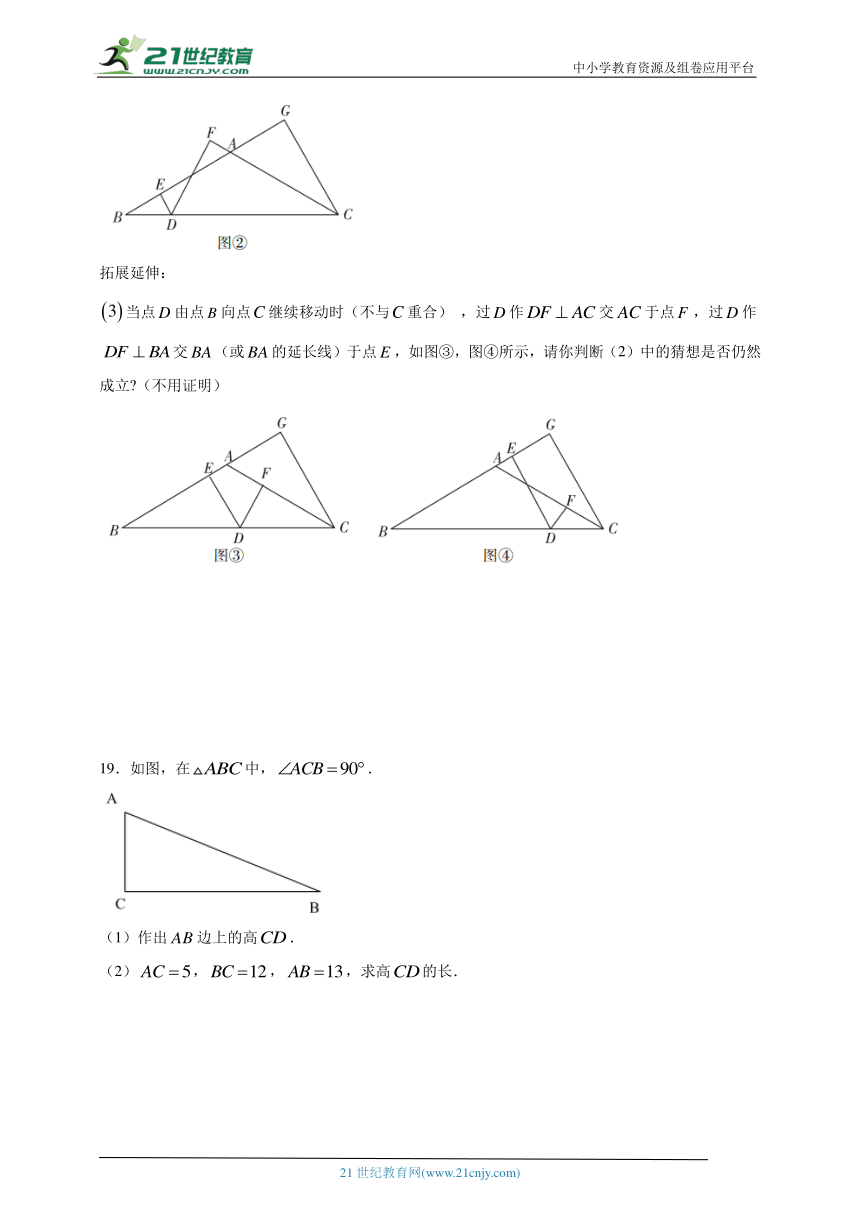
拓展延伸:
当点由点向点继续移动时(不与重合) ,过作交于点,过作交(或的延长线)于点,如图③,图④所示,请你判断(2)中的猜想是否仍然成立 (不用证明)
19.如图,在中,.
(1)作出边上的高.
(2),,,求高的长.
20.如图,每个小正方形的边长为1,在方格纸内将经过一次平移后得到,图中标出了点B的对应点.根据下列条件利用网格点和三角板(或直尺)画图:
(1)补全;
(2)画出中AB边上的中线CD;
(3)画出中BC边上的高线AE;
参考答案
一选择题
1.【答案】D
【详解】△ABC的高AD是过顶点A与BC垂直的线段,只有D选项符合.故选D.
2.【答案】B
【详解】
解:A.作出的是△ABC中BC边上的高线,故本选项错误;
B.作出的是△ABC中AB边上的高线,故本选项正确;
C.不能作出△ABC中AB边上的高线,故本选项错误;
D.作出的是△ABC中AC边上的高线,故本选项错误;
故选:B.
3.【答案】A
【详解】
由已知条件,得△ABD,△ADE,△ACE,3个三角形的面积都相等,组成了3对,
还有△ABE和△ACD的面积相等,共4对.
故选A.
4.【答案】C
【详解】
解:A、在直角三角形ABC中,S△ABC=BC AC,点B沿CB所在直线远离C点移动时BC增大,则该三角形的面积越大.故A正确;
B、如图,随着点B的移动,∠CAB的度数随之增大.故B正确;
C、BC边上的高是AC,线段AC的长度是不变的.故C错误.
D、如图,随着点B的移动,边AB的长度随之增大.故D正确;
故选:C.
5.【答案】A
【详解】解:∵BD是△ABC的中线,
∴AD=CD,
∵△ABD的周长为11,AB=5,
∴CD+BD=AD+BD=11-5=6,
∵BC=3,
∴△BCD的周长是6+3=9,
故选:A.
6.【答案】C
【分析】根据三角形的三条中线都在三角形内部;三角形的三条角平分线都在三角形内部;三角形三条高可以在内部,也可以在外部,直角三角形有两条高在边上即可作答.
【详解】①三角形的中线、角平分线、高都是线段,故正确;
②三角形的三条角平分线都在三角形内部,且交于同一点,故正确;
③钝角三角形的高有两条在三角形外部,故错误;
④三角形的一条中线把该三角形分成面积相等的两部分,故正确.
所以正确的有3个.
故选:C.
7.【答案】C
【分析】根据中线的性质即可求解.
【详解】三角形的一条中线将三角形的面积平均分成两个面积相等的三角形,
故选:C
8.【答案】D
【分析】根据三角形高的定义进行判断.
【详解】线段AD是△ABC的高,则过点A作对边BC的垂线,则垂线段AD为△ABC的高.
选项A、B、C错误,
故选:D.
9.【答案】B
【分析】通过平行线和角平分线得到相等的角,再根据平行线的性质及等腰三角形的判定和性质解答即可.
【详解】∵∠ABC、∠ACB的平分线相交于点P,
∴∠MBP=∠PBC,∠PCN=∠PCB,
又∵MN∥BC,
∴∠PBC=∠MPB,∠NPC=∠PCB,
∴∠MBP=∠MPB,∠NPC=∠PCN,
∴BM=MP,PN=CN,
∴MN=MP+PN=BM+CN,故②正确,
△BMP和△CNP都是等腰三角形,故③正确,
∵△AMN的周长=AM+AN+MN,MN=BM+CN,
∴△AMN的周长等于AB与AC的和,故④正确,
不能说明,故①错误;
故答案为B.
10.【答案】B
【解析】
分析:过点N作NG⊥BC于G,NE⊥BM于E,NF⊥CM于F,根据角平分线上的点到角的两边的距离相等可得NE=NG=NF,再根据到角的两边距离相等的点在角的平分线上判断出MN平分∠BMC,然后根据三角形内角和等于180°求出∠ABC+∠ACB,再根据角的三等分求出∠MBC+∠MCB的度数,然后利用三角形内角和定理求出∠BMC的度数,从而得解.
详解:如图,过点N作NG⊥BC于G,NE⊥BM于E,NF⊥CM于F,
∵∠ABC的三等分线与∠ACB的三等分线分别交于点M、N,
∴BN平分∠MBC,CN平分∠MCB,
∴NE=NG,NF=NG,
∴NE=NF,
∴MN平分∠BMC,
∴∠BMN=∠BMC,
∵∠A=60°,
∴∠ABC+∠ACB=180° ∠A=180° 60°=120°,
根据三等分,∠MBC+∠MCB= (∠ABC+∠ACB)=×120°=80°.
在△BMC中,∠BMC=180° (∠MBC+∠MCB)=180° 80°=100°.
∴∠BMN=×100°=50°;
故选:B.
填空题
11.【答案】3
【分析】
求得AB的长,根据三角形的面积公式即可确定C所在直线,从而确定C的位置.
【详解】
AB=3,设C到AB的距离是a,则×3a=3,
解得a=2,
则C在到AB的距离是2,且与AB平行是直线上,则在第四象限满足条件的格点有3个.
故答案为:3.
12.【答案】1.9
【分析】
过点C作CD⊥AB的延长线于点D,测量出AB,CD的长,再利用三角形的面积公式即可求出△ABC的面积.
【详解】
解:过点C作CD⊥AB的延长线于点D,如图所示.
经过测量,AB=2.2cm,CD=1.7cm,
(cm2).
故答案为1.9.
13.【答案】②
【分析】
根据三角形的中线性质可得答案.
【详解】
根据三角形的中线平分三角形的面积可得②正确,
故答案为②.
14.【答案】2
【分析】S△ADF-S△BEF=S△ABD-S△ABE,所以求出三角形ABD的面积和三角形ABE的面积即可,因为BC=3BE,点D是AC的中点,且S△ABC=12,就可以求出三角形ABD的面积和三角形ABE的面积.
【详解】∵点D是AC的中点,
∴AD=AC,
∵S△ABC=12,
∴S△ABD=S△ABC=×12=6.
∵BC=3BE,
∴S△ABE=S△ABC=×12=4,
∵S△ABD-S△ABE=(S△ADF+S△ABF)-(S△ABF+S△BEF)=S△ADF-S△BEF,
即S△ADF-S△BEF=S△ABD-S△ABE=6-4=2,
故答案为:2.
15.【答案】72020
【分析】连接AB1、BC1、CA1,根据等底等高的三角形面积相等,可得=7S△ABC,由此即可解题.
【详解】连接AB1、BC1、CA1,根据等底等高的三角形面积相等,
△A1BC、△A1B1C、△AB1C、△AB1C1、△ABC1、△A1BC1、△ABC的面积都相等,
所以,=7S△ABC,
同理=7=72S△ABC,
依此类推,△A2020B2020C2020的面积为=72020S△ABC,
∵△ABC的面积为1,
∴=72020.
故答案为:72020.
解答题
16.【答案】(1)点,,的坐标分别是,,;(2)3;(3)见解析
【分析】(1)根据点,,所在位置直接写出的坐标即可;
(2)先求出BC,点A到BC边的距离,利用面积公式BC边上的高求即可;
(3)先求A′(-4,-4),B(-3,-2),C(0,-2)三点坐标,再描出A′、B′、C′三点坐标,连结A′B′、B′C′、C′A′即可.
【详解】(1)点,,的坐标分别是,,;
(2)BC=4-1=3,点A到BC边的距离为:3-1=2,
∴BC边上的高= ;
(3)先把A、B、C三点向左平移4个单位长度,再向下平移5个单位长度,得到A′(-4,-4),B(-3,-2),C(0,-2)三点坐标,再描出A′、B′、C′三点坐标,连结A′B′、B′C′、C′A′,
则为所求如图所示.
17.【答案】(1)6cm;(2)不能求出的长,理由见解析
【分析】(1)根据,及的周长为,可求得BC,再根据三角形中线的性质解答即可;
(2)利用(1)中的方法,求得BC的长度,然后根据构成三角形的条件,可判断出△ABC不存在,进而可知没法求DC的长.
【详解】(1)∵,,
∴,
又∵的周长为,
∴,
∴,
又∵是边上的中线,
∴;
(2)不能,理由如下:
∵,,
∴,
又∵的周长为,
∴,
∴,
∴BC+AC=16∴不能构成三角形,故不能求出DC的长.
18.【答案】(1)证明见解析;(2),证明见解析;(3)结论不变:
【分析】(1)根据,, 即可解决问题;
(2)结论,利用面积法证明即可;
(3)结论不变,证明方法类似(2).
【详解】(1)证明:如图①中,
∵,
∴,,
∴,
又∵,
∴;
(2)解:结论,
理由:如图②中,连接,
∵,,,,
∴,
∵,
∴;
(3)结论不变:,证明如下:
如图③,连接AD,
∵,,,,
∴,
∵,
∴;
如图④,连接AD,
∵,,,,
∴,
∵,
∴.
19.【答案】(1)见解析 (2)
【分析】(1)过C点作CD⊥AB即可;
(2)根据三角形的面积求解即可.
【详解】(1)如图:
(2)∵在中,,,,∠ACB=90°,
∴S△ABC=AC×BC=AB×CD,
∴
20.【答案】(1)图见解析;(2)图见解析;(3)图见解析.
【分析】(1)先根据平移的特点找出,再顺次连接点即可得;
(2)先找出AB边的中点,再连接CD即可得;
(3)过点A作BC所在直线的垂线即可得.
【详解】(1)先根据平移的特点找出,再顺次连接点即可得,如图所示:
(2)先找出AB边的中点,再连接CD即可得,如图所示:
(3)过点A作BC所在直线的垂线即为BC边上的高线AE,如图所示:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级上册数学 1.2三角形的高线、中线与角平分线 同步练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.下列各组图形中,AD是的高的图形是
A. B. C. D.
2.如图,用三角板作的边上的高线,下列三角板的摆放位置正确的是( )
A. B.C.D.
3.如图,△ABC中,D,E分别是BC上两点,且BD=DE=EC,则图中面积相等的三角形有( )
A.4对 B.5对 C.6对 D.7对
4.如图,在直角三角形ABC中,点B沿CB所在直线远离C点移动,下列说法错误的是( )
A.三角形面积随之增大 B.∠CAB的度数随之增大
C.BC边上的高随之增大 D.边AB的长度随之增大
5.已知BD是的中线,,且的周长为11,则的周长是( )
A.9 B.14 C.16 D.不能确定
6.下列说法正确的个数有( )
①三角形的高、中线、角平分线都是线段;
②三角形的三条角平分线都在三角形内部,且交于同一点;
③三角形的三条高都在三角形内部;
④三角形的一条中线把该三角形分成面积相等的两部分.
A.1个 B.2个 C.3个 D.4个
7.能把一个三角形的面积平均分成两个面积相等的三角形,这条线一定是这个三角形的一条( )
A.角平分线 B.高 C.中线 D.一条边的垂直平分线
8.下面四个图形中,线段是的高的是( )
A. B.
C. D.
9.如图所示,在中,与的平分线交于点,过点作交于点,交于点,那么下列结论:①;②;③和都是等腰三角形;④的周长等于与的和,其中正确的有( )
A.4个 B.3个 C.2个 D.1个
10.如图,在△ABC中,点M、N是∠ABC与∠ACB三等分线的交点.若∠A=60°,则∠BMN的度数为( )
A.45° B.50° C.60° D.65°
填空题(本大题共5小题,每小题4分,共20分。)
如图,在5×5的方格纸中,每个小正方形边长为1,点O、A、B在方格纸的交点(格点)上,在第四象限内的格点上找点C,使△ABC的面积为3,则这样的点C共有个_____个.
12.如图,已知△ABC,通过测量、计算得△ABC的面积约为____cm2.(结果保留一位小数)
13.任意一个三角形被一条中线分成两个三角形,则这两个三角形:①形状相同;②面积相等;③全等.上述说法中,正确的是________ .
14.如图,在△ABC中E是BC上的一点,BC=3BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=12,则S△ADF﹣S△BEF=____.
15.如图,△ABC的面积为1,分别倍长(延长一倍)AB,BC,CA得到△A1B1C1,再分别倍长A1B1,B1C1,C1A1得到△A2B2C2.…按此规律,倍长2020次后得到的△A2020B2020C2020的面积为_____.
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.如图,点,,都落在网格的格点上.
(1)写出点,,的坐标;
(2)求的面积:
(3)把先向左平移4个单位长度,再向下平移5个单位长度,得,画出.
17.已知的周长为,是边上的中线,.
(1)如图,当时,求的长.
(2)若,能否求出的长?为什么?
18.在中,交的延长线于点,点是线段上的一个动点.
特例研究:
当点与点重合时,过作交的延长线于点,如图①所示,通过观察﹑测量与的长度,得到.请给予证明.
猜想证明:
当点由点向点移动到如图②所示的位置时,过作交的延长线于点,过作交于点,此时请你通过观察,测量与的长度,猜想并写出与之间存在的数量关系,并证明你的猜想.
拓展延伸:
当点由点向点继续移动时(不与重合) ,过作交于点,过作交(或的延长线)于点,如图③,图④所示,请你判断(2)中的猜想是否仍然成立 (不用证明)
19.如图,在中,.
(1)作出边上的高.
(2),,,求高的长.
20.如图,每个小正方形的边长为1,在方格纸内将经过一次平移后得到,图中标出了点B的对应点.根据下列条件利用网格点和三角板(或直尺)画图:
(1)补全;
(2)画出中AB边上的中线CD;
(3)画出中BC边上的高线AE;
参考答案
一选择题
1.【答案】D
【详解】△ABC的高AD是过顶点A与BC垂直的线段,只有D选项符合.故选D.
2.【答案】B
【详解】
解:A.作出的是△ABC中BC边上的高线,故本选项错误;
B.作出的是△ABC中AB边上的高线,故本选项正确;
C.不能作出△ABC中AB边上的高线,故本选项错误;
D.作出的是△ABC中AC边上的高线,故本选项错误;
故选:B.
3.【答案】A
【详解】
由已知条件,得△ABD,△ADE,△ACE,3个三角形的面积都相等,组成了3对,
还有△ABE和△ACD的面积相等,共4对.
故选A.
4.【答案】C
【详解】
解:A、在直角三角形ABC中,S△ABC=BC AC,点B沿CB所在直线远离C点移动时BC增大,则该三角形的面积越大.故A正确;
B、如图,随着点B的移动,∠CAB的度数随之增大.故B正确;
C、BC边上的高是AC,线段AC的长度是不变的.故C错误.
D、如图,随着点B的移动,边AB的长度随之增大.故D正确;
故选:C.
5.【答案】A
【详解】解:∵BD是△ABC的中线,
∴AD=CD,
∵△ABD的周长为11,AB=5,
∴CD+BD=AD+BD=11-5=6,
∵BC=3,
∴△BCD的周长是6+3=9,
故选:A.
6.【答案】C
【分析】根据三角形的三条中线都在三角形内部;三角形的三条角平分线都在三角形内部;三角形三条高可以在内部,也可以在外部,直角三角形有两条高在边上即可作答.
【详解】①三角形的中线、角平分线、高都是线段,故正确;
②三角形的三条角平分线都在三角形内部,且交于同一点,故正确;
③钝角三角形的高有两条在三角形外部,故错误;
④三角形的一条中线把该三角形分成面积相等的两部分,故正确.
所以正确的有3个.
故选:C.
7.【答案】C
【分析】根据中线的性质即可求解.
【详解】三角形的一条中线将三角形的面积平均分成两个面积相等的三角形,
故选:C
8.【答案】D
【分析】根据三角形高的定义进行判断.
【详解】线段AD是△ABC的高,则过点A作对边BC的垂线,则垂线段AD为△ABC的高.
选项A、B、C错误,
故选:D.
9.【答案】B
【分析】通过平行线和角平分线得到相等的角,再根据平行线的性质及等腰三角形的判定和性质解答即可.
【详解】∵∠ABC、∠ACB的平分线相交于点P,
∴∠MBP=∠PBC,∠PCN=∠PCB,
又∵MN∥BC,
∴∠PBC=∠MPB,∠NPC=∠PCB,
∴∠MBP=∠MPB,∠NPC=∠PCN,
∴BM=MP,PN=CN,
∴MN=MP+PN=BM+CN,故②正确,
△BMP和△CNP都是等腰三角形,故③正确,
∵△AMN的周长=AM+AN+MN,MN=BM+CN,
∴△AMN的周长等于AB与AC的和,故④正确,
不能说明,故①错误;
故答案为B.
10.【答案】B
【解析】
分析:过点N作NG⊥BC于G,NE⊥BM于E,NF⊥CM于F,根据角平分线上的点到角的两边的距离相等可得NE=NG=NF,再根据到角的两边距离相等的点在角的平分线上判断出MN平分∠BMC,然后根据三角形内角和等于180°求出∠ABC+∠ACB,再根据角的三等分求出∠MBC+∠MCB的度数,然后利用三角形内角和定理求出∠BMC的度数,从而得解.
详解:如图,过点N作NG⊥BC于G,NE⊥BM于E,NF⊥CM于F,
∵∠ABC的三等分线与∠ACB的三等分线分别交于点M、N,
∴BN平分∠MBC,CN平分∠MCB,
∴NE=NG,NF=NG,
∴NE=NF,
∴MN平分∠BMC,
∴∠BMN=∠BMC,
∵∠A=60°,
∴∠ABC+∠ACB=180° ∠A=180° 60°=120°,
根据三等分,∠MBC+∠MCB= (∠ABC+∠ACB)=×120°=80°.
在△BMC中,∠BMC=180° (∠MBC+∠MCB)=180° 80°=100°.
∴∠BMN=×100°=50°;
故选:B.
填空题
11.【答案】3
【分析】
求得AB的长,根据三角形的面积公式即可确定C所在直线,从而确定C的位置.
【详解】
AB=3,设C到AB的距离是a,则×3a=3,
解得a=2,
则C在到AB的距离是2,且与AB平行是直线上,则在第四象限满足条件的格点有3个.
故答案为:3.
12.【答案】1.9
【分析】
过点C作CD⊥AB的延长线于点D,测量出AB,CD的长,再利用三角形的面积公式即可求出△ABC的面积.
【详解】
解:过点C作CD⊥AB的延长线于点D,如图所示.
经过测量,AB=2.2cm,CD=1.7cm,
(cm2).
故答案为1.9.
13.【答案】②
【分析】
根据三角形的中线性质可得答案.
【详解】
根据三角形的中线平分三角形的面积可得②正确,
故答案为②.
14.【答案】2
【分析】S△ADF-S△BEF=S△ABD-S△ABE,所以求出三角形ABD的面积和三角形ABE的面积即可,因为BC=3BE,点D是AC的中点,且S△ABC=12,就可以求出三角形ABD的面积和三角形ABE的面积.
【详解】∵点D是AC的中点,
∴AD=AC,
∵S△ABC=12,
∴S△ABD=S△ABC=×12=6.
∵BC=3BE,
∴S△ABE=S△ABC=×12=4,
∵S△ABD-S△ABE=(S△ADF+S△ABF)-(S△ABF+S△BEF)=S△ADF-S△BEF,
即S△ADF-S△BEF=S△ABD-S△ABE=6-4=2,
故答案为:2.
15.【答案】72020
【分析】连接AB1、BC1、CA1,根据等底等高的三角形面积相等,可得=7S△ABC,由此即可解题.
【详解】连接AB1、BC1、CA1,根据等底等高的三角形面积相等,
△A1BC、△A1B1C、△AB1C、△AB1C1、△ABC1、△A1BC1、△ABC的面积都相等,
所以,=7S△ABC,
同理=7=72S△ABC,
依此类推,△A2020B2020C2020的面积为=72020S△ABC,
∵△ABC的面积为1,
∴=72020.
故答案为:72020.
解答题
16.【答案】(1)点,,的坐标分别是,,;(2)3;(3)见解析
【分析】(1)根据点,,所在位置直接写出的坐标即可;
(2)先求出BC,点A到BC边的距离,利用面积公式BC边上的高求即可;
(3)先求A′(-4,-4),B(-3,-2),C(0,-2)三点坐标,再描出A′、B′、C′三点坐标,连结A′B′、B′C′、C′A′即可.
【详解】(1)点,,的坐标分别是,,;
(2)BC=4-1=3,点A到BC边的距离为:3-1=2,
∴BC边上的高= ;
(3)先把A、B、C三点向左平移4个单位长度,再向下平移5个单位长度,得到A′(-4,-4),B(-3,-2),C(0,-2)三点坐标,再描出A′、B′、C′三点坐标,连结A′B′、B′C′、C′A′,
则为所求如图所示.
17.【答案】(1)6cm;(2)不能求出的长,理由见解析
【分析】(1)根据,及的周长为,可求得BC,再根据三角形中线的性质解答即可;
(2)利用(1)中的方法,求得BC的长度,然后根据构成三角形的条件,可判断出△ABC不存在,进而可知没法求DC的长.
【详解】(1)∵,,
∴,
又∵的周长为,
∴,
∴,
又∵是边上的中线,
∴;
(2)不能,理由如下:
∵,,
∴,
又∵的周长为,
∴,
∴,
∴BC+AC=16
18.【答案】(1)证明见解析;(2),证明见解析;(3)结论不变:
【分析】(1)根据,, 即可解决问题;
(2)结论,利用面积法证明即可;
(3)结论不变,证明方法类似(2).
【详解】(1)证明:如图①中,
∵,
∴,,
∴,
又∵,
∴;
(2)解:结论,
理由:如图②中,连接,
∵,,,,
∴,
∵,
∴;
(3)结论不变:,证明如下:
如图③,连接AD,
∵,,,,
∴,
∵,
∴;
如图④,连接AD,
∵,,,,
∴,
∵,
∴.
19.【答案】(1)见解析 (2)
【分析】(1)过C点作CD⊥AB即可;
(2)根据三角形的面积求解即可.
【详解】(1)如图:
(2)∵在中,,,,∠ACB=90°,
∴S△ABC=AC×BC=AB×CD,
∴
20.【答案】(1)图见解析;(2)图见解析;(3)图见解析.
【分析】(1)先根据平移的特点找出,再顺次连接点即可得;
(2)先找出AB边的中点,再连接CD即可得;
(3)过点A作BC所在直线的垂线即可得.
【详解】(1)先根据平移的特点找出,再顺次连接点即可得,如图所示:
(2)先找出AB边的中点,再连接CD即可得,如图所示:
(3)过点A作BC所在直线的垂线即为BC边上的高线AE,如图所示:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
