人教版数学八年级上册11.2.1三角形的内角 精品同步练习(含解析)
文档属性
| 名称 | 人教版数学八年级上册11.2.1三角形的内角 精品同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-13 00:00:00 | ||
图片预览



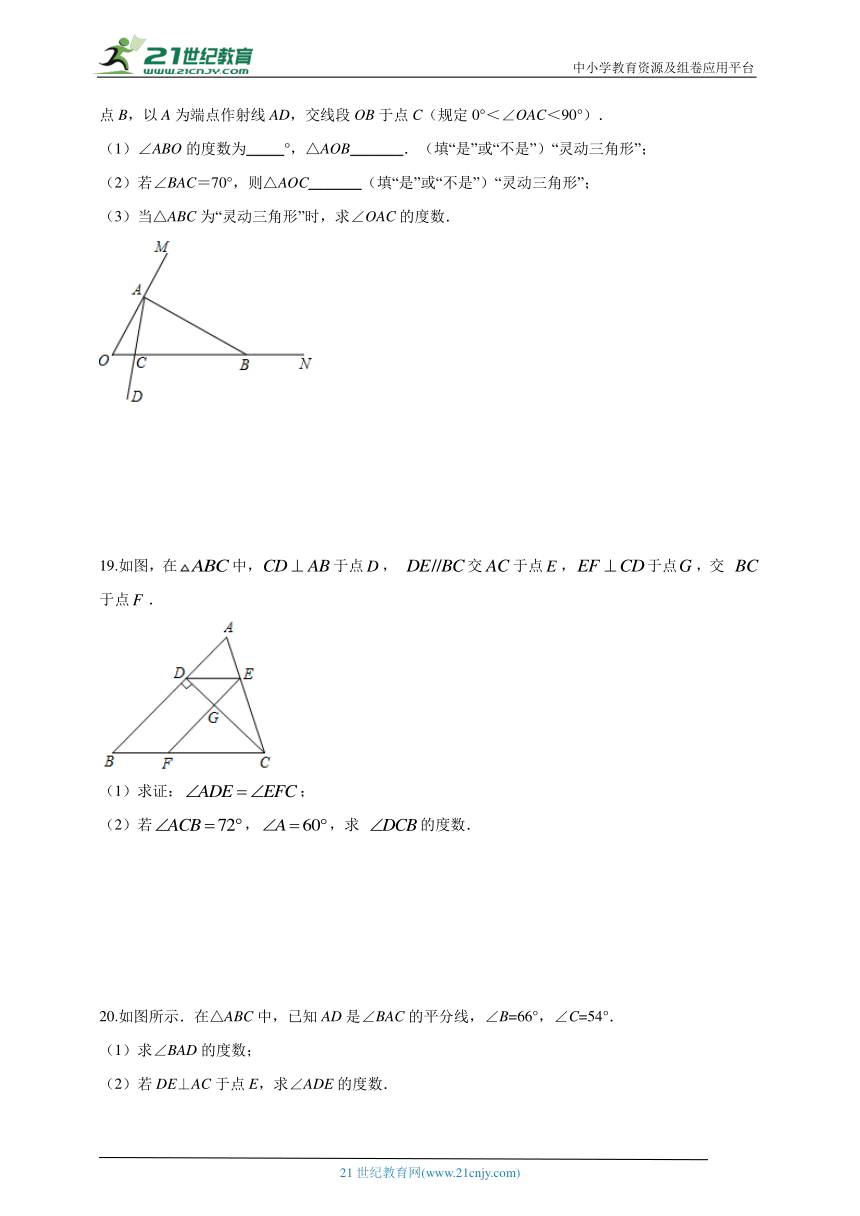
文档简介
中小学教育资源及组卷应用平台
人教版八年级上册数学 11.2.1三角形的内角 同步练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.Rt△ABC中,∠C=90°,∠B=46°,则∠A=
A.44° B.34° C.54° D.64°
2.如图,AB⊥BD,AC⊥CD,∠D=35°,则∠A的度数为
A.65° B.35° C.55° D.45°
3.直角三角形中两锐角之差为20°,则较大锐角为
A.45° B.55° C.65° D.50°
4.如图,是的角平分线,,垂足为,交于,连结.若,,则的度数为( )
A. B. C. D.
5.如图,AE、AD分别是的高和角平分线,且,,则的度数为( )
A.18° B.22° C.30° D.38°
6.如图,在折纸活动中,小明制作了一张纸片,点分别是边上的点,将沿着折叠压平,与重合,若,则( )
A. B. C. D.
7.如图,的一边上有一动点E,连结,在射线上任取一点D,连结,分别作的角平分线,交于点F,则下列关系式正确的是( )
A. B.
C. D.
8.如图,直线 被所截,若,,,则的大小是( )
A. B. C. D.
9.如图,在中,, 是边上的高,是边的中线,是的角平分线,交于点,交于点,下面说法正确的是( )
①的面积是的面积的一半;②;③;④.
A.①②③④ B.①② C.①③ D.①④
10.下列命题是真命题的是( )
A.同位角相等 B.算术平方根等于自身的数只有1
C.直角三角形的两锐角互余 D.如果,那么
二、填空题(本大题共5小题,每小题4分,共20分。)
11.如图,AC⊥BC于点C,DE⊥BE于点E,BC平分∠ABE,∠BDE=58°,则∠A=__________°.
12.如图,将△ABC纸片沿DE折叠,点A的对应点为A′,∠B=60°,∠C=80°,则∠1+∠2等于_______.
13.如图,在△ABC中,∠A=50°,BE平分∠ABC,CE平分外角∠ACD,则∠E的度数为________.
14.在一个三角形中,若其中一个内角的度数是另一个内角的2倍,则我们称这个三角形为“倍角三角形”.已知某“倍角三角形”的一个内角的度数为60°,则其它两个内角的度数分别是_______.
15.如图,________° .
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.如图,AD是△ABC边上的高,BE平分∠ABC交AD于点E.若∠C=60°,∠BED=70°.求∠ABC和∠BAC的度数.
17.探究:如图①,,平分,平分,且点、、均在直线上,直线分别与、交于点、.
(1)若,,则______.
(2)若,求的度数.
拓展:如图②,和的平分线、交于点,经过点且平行于,分别与、交于点、.若,直接写出的度数.(用含的代数式表示)
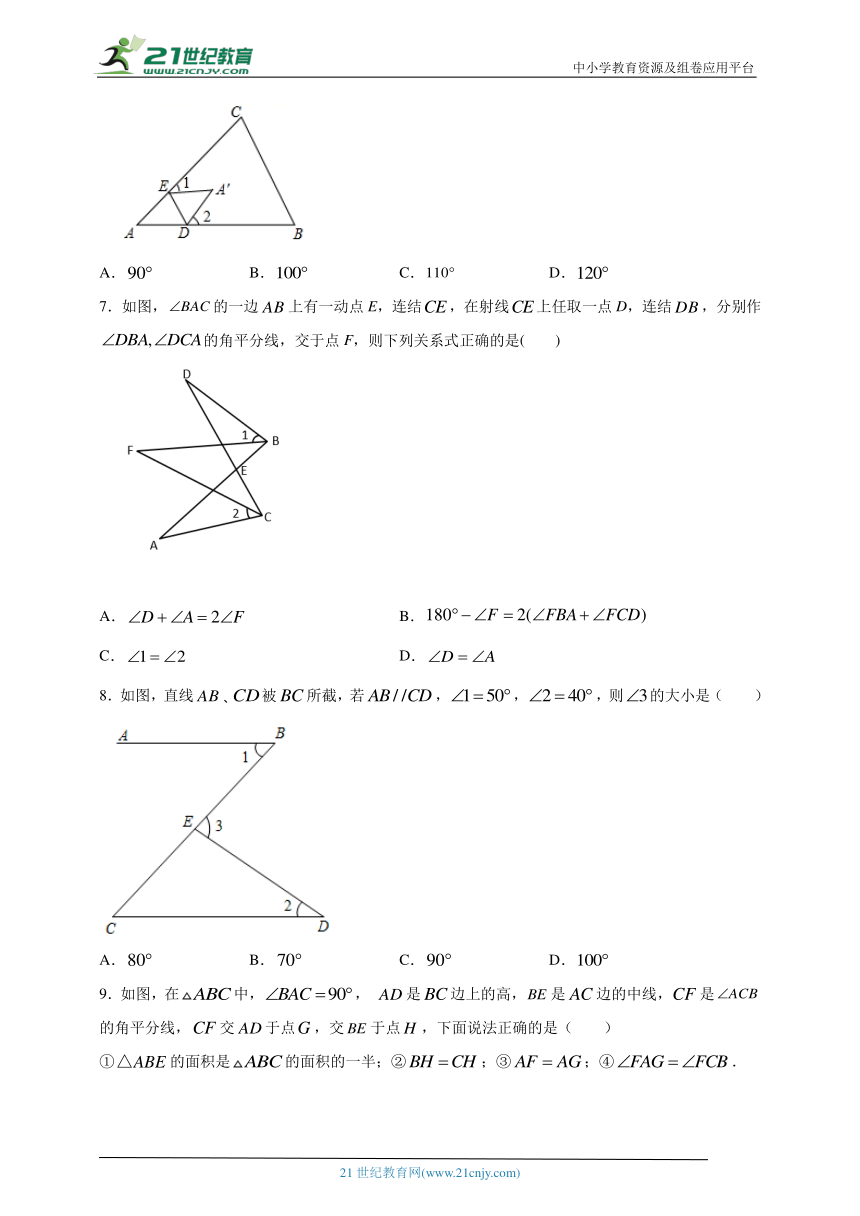
18.在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.例如,三个内角分别为120°、40°、20°的三角形是“灵动三角形”;三个内角分别为80°、75°、25°的三角形也是“灵动三角形”等等.如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°<∠OAC<90°).
(1)∠ABO的度数为_____°,△AOB_______.(填“是”或“不是”)“灵动三角形”;
(2)若∠BAC=70°,则△AOC_______(填“是”或“不是”)“灵动三角形”;
(3)当△ABC为“灵动三角形”时,求∠OAC的度数.
19.如图,在中,于点, 交于点,于点,交 于点.
(1)求证:;
(2)若,,求 的度数.
20.如图所示.在△ABC中,已知AD是∠BAC的平分线,∠B=66°,∠C=54°.
(1)求∠BAD的度数;
(2)若DE⊥AC于点E,求∠ADE的度数.
参考答案
选择题
1.【答案】A
【解析】∵∠C=90°,∠B=46°,∴∠A=90°-46°=44°.故选A.
2.【答案】B
【解析】∵AB⊥BD,AC⊥CD,∴∠B=∠C=90°,∴∠A+∠AEB=∠D+∠CED=90°.又∵∠AEB=∠CED,∴∠A=∠D=35°.故选B.
3.【答案】B
【解析】∵AB⊥BD,AC⊥CD,∴∠B=∠C=90°,∴∠A+∠AEB=∠D+∠CED=90°.又∵∠AEB=∠CED,∴∠A=∠D=35°.故选B.
4.【答案】B
【分析】由角平分线的性质得到,由三角形内角和定理可求得∠BAC,又有可求得∠BAF,继而根据∠EAD=∠BAC-∠BAF进行求解即可.
【详解】,
,
∵BD平分∠ABC,
,
,
,
,
,
故选:B.
5.【答案】B
【分析】根据角平分线性质和三角形内角和定理求解即可;
【详解】∵AE是的高,
∴,
又∵AD是的角平分线,
∴,
∵,,
∴,
∴,
∴;
故答案选B.
6.【答案】B
【分析】根据三角形的内角和等于180°求出∠ADE+∠AED,再根据翻折变换的性质可得∠A′DE=∠ADE,∠A′ED=∠AED,然后利用平角等于180°列式计算即可得解.
【详解】∵∠A=50°,
∴∠ADE+∠AED=180°-50°=130°,
∵△ABC沿着DE折叠压平,A与A′重合,
∴∠A′DE=∠ADE,∠A′ED=∠AED,
∴∠1+∠2=180°-(∠A′ED+∠AED)+180°-(∠A′DE+∠ADE)=360°-2×130°=100°.
故选:B.
7.【答案】A
【分析】判断选项、选项,需假设选项正确,即,再根据角平分线的性质,即可证明得出,此时选项也正确,故选项、选项都不对.对于选项、选项,令与交点为,根据三角形内角和为即可证明选项正确,选项错误.
【详解】当时,,
则,
∵、平分、,
则,
故选项、选项不对.
令与交点为,
在中,,
在中,,
在中,,
在中,,
故,
则选项正确,选项错误.
故选:.
8.【答案】C
【分析】先根据平行线的性质求出,再由三角形外角性质即可得解;
【详解】∵,,
∴,
∵,
∴;
故答案选C.
9.【答案】C
【分析】根据三角形的面积公式进行判断①,根据等腰三角形的判定判断②即可,根据三角形的内角和定理求出∠AFG=∠AGF,再根据等腰三角形的判定判断③即可,根据三角形的内角和定理求出∠FAG=∠ACB,再判断④即可.
【详解】∵BE是AC边的中线,
∴AE=CEAC,
∵△ABE的面积×AE×AB,△ABC的面积×AC×AB,
∴△ABE的面积等于△ABC的面积的一半,故①正确;
根据已知不能推出∠HBC=∠HCB,即不能推出HB=HC,故②错误;
∵在△ACF和△DGC中,∠BAC=∠ADC=90°,∠ACF=∠FCB,
∴∠AFG=90°-∠ACF,∠AGF=∠DGC=90°-∠FCB,
∴∠AFG=∠AGF,
∴AF=AG,故③正确;
∵AD是BC边上的高,
∴∠ADC=90°,
∵∠BAC=90°,
∴∠DAC+∠ACB=90°,∠FAG+∠DAC=90°,
∴∠FAG=∠ACB,
∵CF是∠ACB的角平分线,
∴∠ACF=∠FCB,∠ACB=2∠FCB,
∴∠FAG=2∠FCB,故④错误;
即正确的为①③,
故选:C.
10.【答案】C
【分析】根据同位角的定义、算术平方根的意义、直角三角形的性质、等式的性质判断即可.
【详解】A、同位角不一定相等,原命题是假命题;
B、算术平方根等于自身的数有1和0,原命题是假命题;
C、直角三角形两锐角互余,是真命题;
D、如果a2=b2,那么a=b或a=-b,原命题是假命题;
故选:C.
填空题
11.【答案】58
【解析】∵BC平分∠ABE,∴∠ABC=∠DBE,∵AC⊥BC,DE⊥BE,
∴∠A+∠ABC=90°,∠BDE+∠DBE=90°,
∴∠A=∠BDE=58°.故答案为:58.
12.【答案】80°
【分析】根据平角定义和折叠的性质,得∠1+∠2=360°﹣2(∠3+∠4),再利用三角形的内角和定理得∠3+∠4=∠B+∠C,即可解决问题.
【详解】根据平角的定义和折叠的性质,得
∠1+∠2=360°﹣2(∠3+∠4).
又∵∠3+∠4=180°﹣∠A,∠A+∠B+∠C=180°,
∴∠3+∠4=∠B+∠C,
∵∠B=60°,∠C=80°,
∴∠3+∠4=∠B+∠C=140°,
∴∠1+∠2=80°.
故答案为:80°.
13.【答案】25°
【分析】根据角平分线定义得出∠ABC=2∠EBC,∠ACD=2∠DCE,根据三角形外角性质得出2∠E+∠ABC=∠A+∠ABC,求出∠A=2∠E,即可求出答案.
【详解】∵BE平分∠ABC,CE平分∠ACD,
∴∠ABC=2∠EBC,∠ACD=2∠DCE,
∵∠ACD=2∠DCE=∠A+∠ABC,∠DCE=∠E+∠EBC,
∴2∠DCE=2∠E+2∠EBC,
∴2∠E+∠ABC=∠A+∠ABC,
∴∠A=2∠E,
∵∠A=50°,
∴∠E=25°,
故答案为:25°.
14.【答案】30°,90°或40°,80°
【分析】根据“倍角三角形”的定义结合三角形的内角和定理分三种情况即可得出结论.
【详解】在△ABC中,不妨设∠A=60,
①若∠A=2∠C,则∠C=30,
∴∠B=;
②若∠C=2∠A,则∠C=120,
∴∠B=(不合题意,舍去);
③若∠B=2∠C,则3∠C=120,
∴∠C0,∠B=;
综上所述,其它两个内角的度数分别是:30,90或40,80.
15.【答案】180
【分析】连接AB,可知∠C+∠D=∠CAB+∠DBA,进而根据三角形内角和求出的值.
【详解】连接AB,∵∠C+∠D+∠DFC=∠CAB+∠DBA+∠AFB,∠DFC=∠AFB,
∴∠C+∠D=∠CAB+∠DBA,
,
,
=180°
故答案为:180.
解答题
16.【解析】∵AD是△ABC的高,
∴∠ADB=90°,
又∵∠BED=70°,
∴.
∵BE平分∠ABC,
∴∠ABC=2∠DBE=40°.
又∵∠BAC+∠ABC+∠C=180°,∠C=60°,
∴∠BAC=180°-∠ABC-∠C=80°.
17.【答案】探究:(1)120°;(2)125°;拓展:
【分析】(1)先根据角平分线的定义求出∠OFH,∠FHO的度数,再根据三角形的内角和定理求出∠FOH的度数;
(2)先根据角平分线的定义求出∠OFH+∠FHO的度数,再根据三角形的内角和定理求出∠FOH的度数;
(拓展)先根据角平分线的定义求出∠OFH=∠AFH,∠OHI=∠CHI=(180°-∠CHF),再根据两直线平行内错角相等得∠FOH=∠OHI﹣∠OFH即可.
【详解】(1)∵∠AFH=80°,OF平分∠AFH,
∴∠OFH=40°,
又∵EG∥FH,
∴∠EOF=∠OFH=40°;
∵∠CHF=40°,OH平分∠CHF,
∴∠FHO=20°,
∴△FOH中,∠FOH=180°﹣∠OFH﹣∠OHF=120°;
故填:120°;
(2)∵平分,平分,
∴,.
∵,
∴.
∵,
∴.
拓展:
∵平分,平分,
∴,,
∴
.
.
18.【答案】(1)30;是;(2)是;(3)30°或52.5°或80°.
【分析】(1)利用三角形内角和定理解决问题即可.
(2)求出∠OAC即可解决问题.
(3)分三种情形分别求出即可.
【详解】(1)∵AB⊥OM,
∴∠BAO=90°,
∵∠AOB=60°,
∴∠ABO=90°﹣60°=30°,
∵90°=3×30°,
∴△AOB是“灵动三角形”.
故答案为:30,是.
(2)∵∠OAB=90°,∠BAC=70°,
∴∠OAC=20°,
∵∠AOC=60°=3×20°,
∴△AOC是“灵动三角形”.
故答案为:是.
(3:①当∠ACB=3∠ABC时,∵∠ABO=30°,
∴∠ACB=90°,
∴∠CAB=60°,
∴∠OAC=30°;
②当∠ABC=3∠CAB时,
∵∠ABO=30°,
∴∠CAB=10°,
∵∠OAB=90°,
∴∠OAC=80°.
③当∠ACB=3∠CAB时,
∵∠ABO=30°,
∴4∠CAB=150°,
∴∠CAB=37.5°,
∴∠OAC=52.5°.
综上所述,满足条件的值为30°或52.5°或80°.
19.【答案】(1)证明见详解;(2).
【分析】(1)根据平行线的判定和性质定理即可得到结论;
(2)根据三角形的内角和定理即可得到结论.
【详解】(1)证明:,
,
,,
,
,
;
(2)解:,,
,
,
,
.
20.【答案】(1)30°;(2)60°
【分析】(1)先根据三角形内角和定理求出∠BAC的度数,再根据角平分线的性质求出∠BAD的度数;
(2)根据三角形内角和定理即可得出结论.
【详解】(1)∵在△ABC中,∠B=66°,∠C=54°,∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C=60°.
∵AD是△ABC的角平分线,
∴∠BAD=∠BAC=30°;
(2)∵∠CAD=∠BAC=30°,又DE⊥AC,
∴在Rt△ADE中,∠EAD=30°,
∴∠ADE=90°-∠EAD=60°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级上册数学 11.2.1三角形的内角 同步练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.Rt△ABC中,∠C=90°,∠B=46°,则∠A=
A.44° B.34° C.54° D.64°
2.如图,AB⊥BD,AC⊥CD,∠D=35°,则∠A的度数为
A.65° B.35° C.55° D.45°
3.直角三角形中两锐角之差为20°,则较大锐角为
A.45° B.55° C.65° D.50°
4.如图,是的角平分线,,垂足为,交于,连结.若,,则的度数为( )
A. B. C. D.
5.如图,AE、AD分别是的高和角平分线,且,,则的度数为( )
A.18° B.22° C.30° D.38°
6.如图,在折纸活动中,小明制作了一张纸片,点分别是边上的点,将沿着折叠压平,与重合,若,则( )
A. B. C. D.
7.如图,的一边上有一动点E,连结,在射线上任取一点D,连结,分别作的角平分线,交于点F,则下列关系式正确的是( )
A. B.
C. D.
8.如图,直线 被所截,若,,,则的大小是( )
A. B. C. D.
9.如图,在中,, 是边上的高,是边的中线,是的角平分线,交于点,交于点,下面说法正确的是( )
①的面积是的面积的一半;②;③;④.
A.①②③④ B.①② C.①③ D.①④
10.下列命题是真命题的是( )
A.同位角相等 B.算术平方根等于自身的数只有1
C.直角三角形的两锐角互余 D.如果,那么
二、填空题(本大题共5小题,每小题4分,共20分。)
11.如图,AC⊥BC于点C,DE⊥BE于点E,BC平分∠ABE,∠BDE=58°,则∠A=__________°.
12.如图,将△ABC纸片沿DE折叠,点A的对应点为A′,∠B=60°,∠C=80°,则∠1+∠2等于_______.
13.如图,在△ABC中,∠A=50°,BE平分∠ABC,CE平分外角∠ACD,则∠E的度数为________.
14.在一个三角形中,若其中一个内角的度数是另一个内角的2倍,则我们称这个三角形为“倍角三角形”.已知某“倍角三角形”的一个内角的度数为60°,则其它两个内角的度数分别是_______.
15.如图,________° .
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.如图,AD是△ABC边上的高,BE平分∠ABC交AD于点E.若∠C=60°,∠BED=70°.求∠ABC和∠BAC的度数.
17.探究:如图①,,平分,平分,且点、、均在直线上,直线分别与、交于点、.
(1)若,,则______.
(2)若,求的度数.
拓展:如图②,和的平分线、交于点,经过点且平行于,分别与、交于点、.若,直接写出的度数.(用含的代数式表示)
18.在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.例如,三个内角分别为120°、40°、20°的三角形是“灵动三角形”;三个内角分别为80°、75°、25°的三角形也是“灵动三角形”等等.如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°<∠OAC<90°).
(1)∠ABO的度数为_____°,△AOB_______.(填“是”或“不是”)“灵动三角形”;
(2)若∠BAC=70°,则△AOC_______(填“是”或“不是”)“灵动三角形”;
(3)当△ABC为“灵动三角形”时,求∠OAC的度数.
19.如图,在中,于点, 交于点,于点,交 于点.
(1)求证:;
(2)若,,求 的度数.
20.如图所示.在△ABC中,已知AD是∠BAC的平分线,∠B=66°,∠C=54°.
(1)求∠BAD的度数;
(2)若DE⊥AC于点E,求∠ADE的度数.
参考答案
选择题
1.【答案】A
【解析】∵∠C=90°,∠B=46°,∴∠A=90°-46°=44°.故选A.
2.【答案】B
【解析】∵AB⊥BD,AC⊥CD,∴∠B=∠C=90°,∴∠A+∠AEB=∠D+∠CED=90°.又∵∠AEB=∠CED,∴∠A=∠D=35°.故选B.
3.【答案】B
【解析】∵AB⊥BD,AC⊥CD,∴∠B=∠C=90°,∴∠A+∠AEB=∠D+∠CED=90°.又∵∠AEB=∠CED,∴∠A=∠D=35°.故选B.
4.【答案】B
【分析】由角平分线的性质得到,由三角形内角和定理可求得∠BAC,又有可求得∠BAF,继而根据∠EAD=∠BAC-∠BAF进行求解即可.
【详解】,
,
∵BD平分∠ABC,
,
,
,
,
,
故选:B.
5.【答案】B
【分析】根据角平分线性质和三角形内角和定理求解即可;
【详解】∵AE是的高,
∴,
又∵AD是的角平分线,
∴,
∵,,
∴,
∴,
∴;
故答案选B.
6.【答案】B
【分析】根据三角形的内角和等于180°求出∠ADE+∠AED,再根据翻折变换的性质可得∠A′DE=∠ADE,∠A′ED=∠AED,然后利用平角等于180°列式计算即可得解.
【详解】∵∠A=50°,
∴∠ADE+∠AED=180°-50°=130°,
∵△ABC沿着DE折叠压平,A与A′重合,
∴∠A′DE=∠ADE,∠A′ED=∠AED,
∴∠1+∠2=180°-(∠A′ED+∠AED)+180°-(∠A′DE+∠ADE)=360°-2×130°=100°.
故选:B.
7.【答案】A
【分析】判断选项、选项,需假设选项正确,即,再根据角平分线的性质,即可证明得出,此时选项也正确,故选项、选项都不对.对于选项、选项,令与交点为,根据三角形内角和为即可证明选项正确,选项错误.
【详解】当时,,
则,
∵、平分、,
则,
故选项、选项不对.
令与交点为,
在中,,
在中,,
在中,,
在中,,
故,
则选项正确,选项错误.
故选:.
8.【答案】C
【分析】先根据平行线的性质求出,再由三角形外角性质即可得解;
【详解】∵,,
∴,
∵,
∴;
故答案选C.
9.【答案】C
【分析】根据三角形的面积公式进行判断①,根据等腰三角形的判定判断②即可,根据三角形的内角和定理求出∠AFG=∠AGF,再根据等腰三角形的判定判断③即可,根据三角形的内角和定理求出∠FAG=∠ACB,再判断④即可.
【详解】∵BE是AC边的中线,
∴AE=CEAC,
∵△ABE的面积×AE×AB,△ABC的面积×AC×AB,
∴△ABE的面积等于△ABC的面积的一半,故①正确;
根据已知不能推出∠HBC=∠HCB,即不能推出HB=HC,故②错误;
∵在△ACF和△DGC中,∠BAC=∠ADC=90°,∠ACF=∠FCB,
∴∠AFG=90°-∠ACF,∠AGF=∠DGC=90°-∠FCB,
∴∠AFG=∠AGF,
∴AF=AG,故③正确;
∵AD是BC边上的高,
∴∠ADC=90°,
∵∠BAC=90°,
∴∠DAC+∠ACB=90°,∠FAG+∠DAC=90°,
∴∠FAG=∠ACB,
∵CF是∠ACB的角平分线,
∴∠ACF=∠FCB,∠ACB=2∠FCB,
∴∠FAG=2∠FCB,故④错误;
即正确的为①③,
故选:C.
10.【答案】C
【分析】根据同位角的定义、算术平方根的意义、直角三角形的性质、等式的性质判断即可.
【详解】A、同位角不一定相等,原命题是假命题;
B、算术平方根等于自身的数有1和0,原命题是假命题;
C、直角三角形两锐角互余,是真命题;
D、如果a2=b2,那么a=b或a=-b,原命题是假命题;
故选:C.
填空题
11.【答案】58
【解析】∵BC平分∠ABE,∴∠ABC=∠DBE,∵AC⊥BC,DE⊥BE,
∴∠A+∠ABC=90°,∠BDE+∠DBE=90°,
∴∠A=∠BDE=58°.故答案为:58.
12.【答案】80°
【分析】根据平角定义和折叠的性质,得∠1+∠2=360°﹣2(∠3+∠4),再利用三角形的内角和定理得∠3+∠4=∠B+∠C,即可解决问题.
【详解】根据平角的定义和折叠的性质,得
∠1+∠2=360°﹣2(∠3+∠4).
又∵∠3+∠4=180°﹣∠A,∠A+∠B+∠C=180°,
∴∠3+∠4=∠B+∠C,
∵∠B=60°,∠C=80°,
∴∠3+∠4=∠B+∠C=140°,
∴∠1+∠2=80°.
故答案为:80°.
13.【答案】25°
【分析】根据角平分线定义得出∠ABC=2∠EBC,∠ACD=2∠DCE,根据三角形外角性质得出2∠E+∠ABC=∠A+∠ABC,求出∠A=2∠E,即可求出答案.
【详解】∵BE平分∠ABC,CE平分∠ACD,
∴∠ABC=2∠EBC,∠ACD=2∠DCE,
∵∠ACD=2∠DCE=∠A+∠ABC,∠DCE=∠E+∠EBC,
∴2∠DCE=2∠E+2∠EBC,
∴2∠E+∠ABC=∠A+∠ABC,
∴∠A=2∠E,
∵∠A=50°,
∴∠E=25°,
故答案为:25°.
14.【答案】30°,90°或40°,80°
【分析】根据“倍角三角形”的定义结合三角形的内角和定理分三种情况即可得出结论.
【详解】在△ABC中,不妨设∠A=60,
①若∠A=2∠C,则∠C=30,
∴∠B=;
②若∠C=2∠A,则∠C=120,
∴∠B=(不合题意,舍去);
③若∠B=2∠C,则3∠C=120,
∴∠C0,∠B=;
综上所述,其它两个内角的度数分别是:30,90或40,80.
15.【答案】180
【分析】连接AB,可知∠C+∠D=∠CAB+∠DBA,进而根据三角形内角和求出的值.
【详解】连接AB,∵∠C+∠D+∠DFC=∠CAB+∠DBA+∠AFB,∠DFC=∠AFB,
∴∠C+∠D=∠CAB+∠DBA,
,
,
=180°
故答案为:180.
解答题
16.【解析】∵AD是△ABC的高,
∴∠ADB=90°,
又∵∠BED=70°,
∴.
∵BE平分∠ABC,
∴∠ABC=2∠DBE=40°.
又∵∠BAC+∠ABC+∠C=180°,∠C=60°,
∴∠BAC=180°-∠ABC-∠C=80°.
17.【答案】探究:(1)120°;(2)125°;拓展:
【分析】(1)先根据角平分线的定义求出∠OFH,∠FHO的度数,再根据三角形的内角和定理求出∠FOH的度数;
(2)先根据角平分线的定义求出∠OFH+∠FHO的度数,再根据三角形的内角和定理求出∠FOH的度数;
(拓展)先根据角平分线的定义求出∠OFH=∠AFH,∠OHI=∠CHI=(180°-∠CHF),再根据两直线平行内错角相等得∠FOH=∠OHI﹣∠OFH即可.
【详解】(1)∵∠AFH=80°,OF平分∠AFH,
∴∠OFH=40°,
又∵EG∥FH,
∴∠EOF=∠OFH=40°;
∵∠CHF=40°,OH平分∠CHF,
∴∠FHO=20°,
∴△FOH中,∠FOH=180°﹣∠OFH﹣∠OHF=120°;
故填:120°;
(2)∵平分,平分,
∴,.
∵,
∴.
∵,
∴.
拓展:
∵平分,平分,
∴,,
∴
.
.
18.【答案】(1)30;是;(2)是;(3)30°或52.5°或80°.
【分析】(1)利用三角形内角和定理解决问题即可.
(2)求出∠OAC即可解决问题.
(3)分三种情形分别求出即可.
【详解】(1)∵AB⊥OM,
∴∠BAO=90°,
∵∠AOB=60°,
∴∠ABO=90°﹣60°=30°,
∵90°=3×30°,
∴△AOB是“灵动三角形”.
故答案为:30,是.
(2)∵∠OAB=90°,∠BAC=70°,
∴∠OAC=20°,
∵∠AOC=60°=3×20°,
∴△AOC是“灵动三角形”.
故答案为:是.
(3:①当∠ACB=3∠ABC时,∵∠ABO=30°,
∴∠ACB=90°,
∴∠CAB=60°,
∴∠OAC=30°;
②当∠ABC=3∠CAB时,
∵∠ABO=30°,
∴∠CAB=10°,
∵∠OAB=90°,
∴∠OAC=80°.
③当∠ACB=3∠CAB时,
∵∠ABO=30°,
∴4∠CAB=150°,
∴∠CAB=37.5°,
∴∠OAC=52.5°.
综上所述,满足条件的值为30°或52.5°或80°.
19.【答案】(1)证明见详解;(2).
【分析】(1)根据平行线的判定和性质定理即可得到结论;
(2)根据三角形的内角和定理即可得到结论.
【详解】(1)证明:,
,
,,
,
,
;
(2)解:,,
,
,
,
.
20.【答案】(1)30°;(2)60°
【分析】(1)先根据三角形内角和定理求出∠BAC的度数,再根据角平分线的性质求出∠BAD的度数;
(2)根据三角形内角和定理即可得出结论.
【详解】(1)∵在△ABC中,∠B=66°,∠C=54°,∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C=60°.
∵AD是△ABC的角平分线,
∴∠BAD=∠BAC=30°;
(2)∵∠CAD=∠BAC=30°,又DE⊥AC,
∴在Rt△ADE中,∠EAD=30°,
∴∠ADE=90°-∠EAD=60°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
