人教版数学八年级上册11.2.2三角形的外角 精品同步练习(含解析)
文档属性
| 名称 | 人教版数学八年级上册11.2.2三角形的外角 精品同步练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-13 19:16:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版八年级上册数学 11.2.2三角形的外角 同步练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.三角形的一个外角,不大于和它相邻的内角,这个三角形一定是
A.锐角三角形 B.直角三角形
C.钝角三角形 D.非锐角三角形
2.下列叙述中正确的是
A.三角形的外角等于两个内角的和
B.三角形的外角大于内角
C.三角形的外角等于与它不相邻的两个内角和
D.三角形每一个内角都只有一个外角
3.一副三角板有两个直角三角形,如图叠放在一起,则∠α的度数是
A.165° B.120° C.150° D.135°
4.如图,把纸片沿DE折叠,点A落在四边形BCED的外部,,,则的度数为( )
A.32° B.30° C.28° D.26°
5.如图,,点在上,,,则下列结论正确的个数是( )
(1);(2);(3);(4)
A.1个 B.2个 C.3个 D.4个
6.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
A.105° B.95° C.85° D.75°
7.如图,在△ABC中,∠ACB=90°,D在AB上,将△ABC沿CD折叠,点B落在AC边上的点B′处,若,则∠A的度数为( )
A.25° B.30° C.35° D.40°
8.如图,和相交于点,,则下列结论中不正确的是( ).
A. B.
C. D.
9.已知,是的边上一点,,和的平分线交于点,若,则的大小为( )
A. B. C. D.
10.下列命题是假命题的是( )
A.三角形的内角和是180° B.两直线平行,内错角相等
C.三角形的外角大于任何一个内角 D.同旁内角互补,两直线平行
填空题(本大题共5小题,每小题4分,共20分。)
11.如图,在△ABC中,∠B=66°,∠C=54°,AD是∠BAC的平分线,DE平分∠ADC交AC于E,则∠ADE=
__________.
12.已知,直线交于点,交于点是直线上一动点,过作直线的垂线交于点.若,则__________.
13.如图,在△ABC中,BD平分∠ABC,连接CD,若∠A=∠D=40°,∠ACD=30°,则∠DCE的度数为_____.
14.如图,,点,分别在射线,上,平分,的反向延长线与的平分线交于点,则的度数是_______.
15.已知,一个含角的直角三角板按如图所示放置,,则_____.
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.已知,如图,点D是中AC边上的一点,点E是BC边延长线上一点,说明:.
17.如图,在△ABC中,D是BC上的一点,∠1=∠2,∠3=∠4,∠B=40°,求∠BAC的度数.
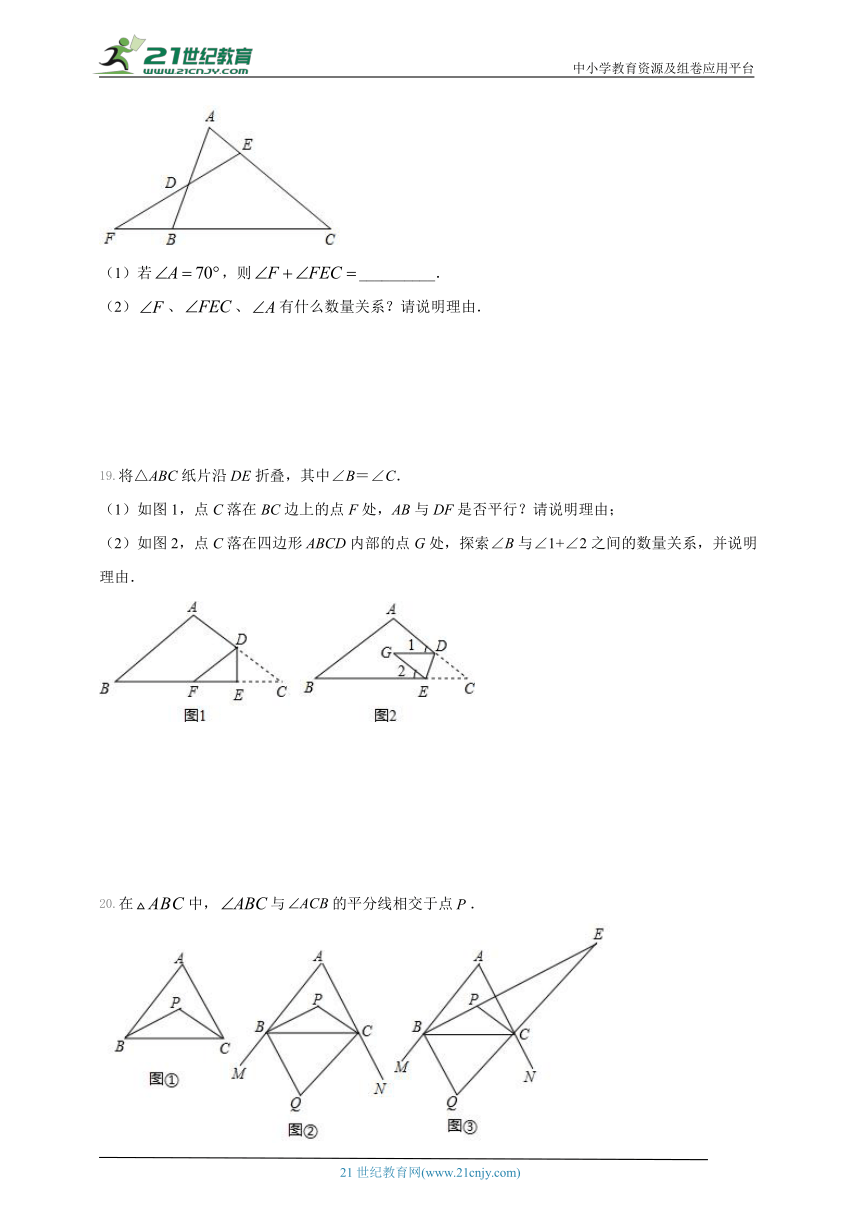
18.如图,在中,,直线分别交的边、和的延长线于点、、.
(1)若,则__________.
(2)、、有什么数量关系?请说明理由.
19.将△ABC纸片沿DE折叠,其中∠B=∠C.
(1)如图1,点C落在BC边上的点F处,AB与DF是否平行?请说明理由;
(2)如图2,点C落在四边形ABCD内部的点G处,探索∠B与∠1+∠2之间的数量关系,并说明理由.
20.在中,与的平分线相交于点.
(1)如图①,如果,求的度数;
(2)如图②,作外角,的角平分线,且交于点,试探索,之间的数量关系;
(3)如图③,在图②中延长线段,交于点若中存在一个内角等于另一个内角的2倍,求的度数.
参考答案
选择题
1.【答案】D
【解析】因为三角形的一个外角与它相邻的内角和为180°,而题中说这个外角不大于它相邻的内角,所以可知与它相邻的这个内角是一个大于或等于90°的角,则这个三角形就是一个钝角三角形或直角三角形.故选D.
2.【答案】C
【解析】A、三角形的外角等于和它不相邻的两个内角的和,故本选项错误;
B、三角形的外角大于和它不相邻的一个内角,故本选项错误.
C、符合三角形外角的性质,故本选项正确;
D、三角形每一个内角都有两个外角,故本选项错误.故选C.
3.【答案】A
【解析】如图,
∵∠2=90°-30°=60°,∴∠1=∠2-45°=15°,∴∠α=180°-∠1=165°.故选A.
4.【答案】C
【分析】根据翻折的性质可得,再利用三角形外角的性质表示出,然后根据角的和差整理即可得解.
【详解】解:如图,由翻折的性质得,
∴,
∴在△ADE中,,
∵,
∴,
∴,
∵,,
∴.
故选:C.
5.【答案】B
【分析】利用平行线的性质和三角形的性质依次判断即可求解.
【详解】解:∵AB∥CD,
∴∠A+∠C=180°,
又∵∠A=110°,
∴∠C=70°,
∴∠AED=∠C+∠D=85°,故(2)正确,
∵∠C+∠D+∠CED=180°,
∴∠D+∠CED=110°,
∴∠A=∠CED+∠D,故(3)正确,
∵点E在AC上的任意一点,
∴AE无法判断等于CE,∠BED无法判断等于45°,故(1)、(4)错误,
故选:B.
6.【答案】C
【分析】根据角平分线的性质,求得∠ACD=120°,利用三角形的外角性质求解即可.
【详解】∵CE是△ABC的外角∠ACD的平分线,∠ACE=60°,
∴∠ACD=120°,
∵∠ACD=∠A+∠B,且∠B=35°,
∴∠A=85°,
故选C.
7.【答案】C
【分析】利用翻折不变性,三角形内角和定理和三角形外角的性质即可解决问题.
【详解】∵∠ACB=90°,
∴∠A+∠B=90°,
∵△CDB′是由△CDB翻折得到,
∴∠CB′D=∠B,
∵∠CB′D=∠A+∠ADB′=∠A+20°,
∴∠A+∠A+20°=90°,
解得∠A=35°.
故选:C.
8.【答案】D
【分析】利用三角形的外角性质,对顶角相等逐一判断即可.
【详解】∵∠1=∠2,∠A=∠C,∠1=∠A+∠D,∠2=∠B+∠C,
∴∠B=∠D,
∴选项A、B正确;
∵∠2=∠A+∠D,
∴,
∴选项C正确;
没有条件说明
故选:D.
9.【答案】C
【分析】先利用角平分线和三角形外角的性质可得,再根据平行线的性质定理即可得出的大小.
【详解】解:如下图所示,
∵和的平分线交于点,
∴,
∵,,
∴,
∵,
∴,
∵,
∴,
故选:C.
10.【答案】C
【分析】根据三角形内角和定理、外角性质、平行线的性质与判定进行判断即可.
【详解】解:A选项,三角形的内角和是180°,是真命题,不符合题意;
B选项,两直线平行,内错角相等,是真命题,不符合题意;
C选项,三角形的外角大于任何一个内角,是假命题,符合题意;
D选项,同旁内角互补,两直线平行,是真命题,不符合题意;
故选:C.
填空题
11.【答案】48°
12.【答案】90°或30°
【分析】先由两直线平行,内错角相等得出∠EFC=∠PEF.若设∠PEF=x,则∠EFC=x,∠APQ=2x,∠EQP=x,再由EF⊥PQ,根据三角形内角和定理得到∠PEF+∠APQ=90°,即x+2x=90°,解方程求出x=30°,然后根据三角形外角的性质即可求出∠AEQ的度数.
【详解】解:①如图:
∵AB∥CD,
∴∠EFC=∠PEF.
设∠PEF=x,则∠EFC=x,∠APQ=2∠EFC=2x,∠EQP=∠EFC=x.
∵EF⊥PQ,
∴∠PEF+∠APQ=90°,即x+2x=90°,
解得x=30°,
∴∠EQP=x=30°,∠APQ=2x=60°,
∴∠AEQ=∠EQP+∠APQ=30°+60°=90°.
②如图:
易知∠EFC=∠FEB=∠HEA,∠APQ=∠HPE,
又∵∠PHE=90°,
故∠EFC=30°,∠EQP=30°,∠APQ=60°;
故∠AEQ=∠APQ ∠EQP=30°.
综上所述:90°或30°.
故答案是:90°或30°.
13.【答案】70°.
【分析】由三角形的外角的性质定理得到∠ACE=∠A+∠ABC,∠DCE=∠CBD+∠D,再由已知∠ABD=∠CBD,∠A=∠D=40°,∠ACD=30°解方程组可求得结果.
【详解】∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵∠ACE=∠A+∠ABC=40°+2∠CBD,
∴∠DCE+∠ACD=∠A+2∠CBD,
∵∠DCE=∠CBD+∠D,∠A=∠D=40°,∠ACD=30°,
∴∠DCE+30°=40°+2∠CBD,即∠DCE=2∠CBD+10°①,
∠DCE=40°+∠CBD②,
由①②得∠DCE=70°,
故答案为:70°.
14.【答案】
【分析】根据三角形的一个外角等于与它不相邻的两个内角的和,列式求出,再根据角平分线的定义求出和,然后根据三角形的一个外角等于与它不相邻的两个内角的和,列式计算即可得解.
【详解】解:根据三角形的外角性质,可得,
平分,平分,
,,
,
,
,
,
,
,
.
故答案为:45°.
15.【答案】75°.
【分析】利用外角求∠5,再根据平行线的性质求∠1.
【详解】解:由题意可知∠4=45°,∠2=∠3=30°,
∠5=∠2+∠3=75°,
∵,
∴∠1=∠5=75°,
故答案为:75°.
解答题
16.【解析】∵∠DCB是△DCE的一个外角,∴∠DCB>∠CDE.
∵∠ADB是△BCD的一个外角,
∴∠ADB>∠DCB,
∴∠ADB>∠CDE.
17.【解析】∵∠1=∠2,∠B=40°,
∴∠2=∠1=(180°-40°)÷2=70°,
又∵∠2是△ADC的外角,∴∠2=∠3+∠4,
∵∠3=∠4,∴∠2=2∠3,
∴∠3=∠2=35°,
∴∠BAC=∠1+∠3=105°.
18.【答案】(1);(2)∠F+∠FEC=2∠A,理由见解析
【分析】(1)在△ABC中,利用三角形内角和定理求得∠C的度数,再在△EFC中,利用三角形内角和定理即可求解;
(2)根据三角形外角的性质,可得出∠FEC=∠A+∠ADE,∠F+∠BDF=∠ABC,再根据∠A=∠ABC,即可得出答案.
【详解】(1)在△ABC中,∠A=∠ABC,且∠A=70°,
∴∠C=,
∴∠F+∠FEC=;
故答案为:;
(2)∠F+∠FEC=2∠A,
理由:∵∠FEC=∠A+∠ADE,∠F+∠BDF=∠ABC,
∴∠F+∠FEC=∠F+∠A+∠ADE,
∵∠ADE=∠BDF,
∴∠F+∠FEC=∠A+∠ABC,
∵∠A=∠ABC,
∴∠F+∠FEC=∠A+∠ABC=2∠A.
19.【答案】(1)平行,理由见解析;(2)∠1+∠2=2∠B,理由见解析
【分析】(1)AB与DF平行.根据翻折可得出∠DFC=∠C,结合∠B=∠C即可得出∠B=∠DFC,从而证出AB∥DF;
(2)连接GC,由翻折可得出∠DGE=∠ACB,再根据三角形外角的性质得出∠1=∠DGC+∠DCG,∠2=∠EGC+∠ECG,通过角的运算即可得出∠1+∠2=2∠B.
【详解】解:(1)AB与DF平行.理由如下:
由翻折,得∠DFC=∠C.
又∵∠B=∠C,
∴∠B=∠DFC,
∴AB∥DF.
(2)连接GC,如图所示.
由翻折,得∠DGE=∠ACB.
∵∠1=∠DGC+∠DCG,∠2=∠EGC+∠ECG,
∴∠1+∠2=∠DGC+∠DCG+∠EGC+∠ECG=(∠DGC+∠EGC)+(∠DCG+∠ECG)=∠DGE+∠DCE=2∠ACB.
∵∠B=∠ACB,
∴∠1+∠2=2∠B.
20.【答案】(1);(2);(3)的度数是90°或60°或120°
【分析】(1)运用三角形的内角和定理及角平分线的定义,首先求出∠PBC+∠PCB,进而求出∠BPC即可解决问题;
(2)根据三角形的外角性质分别表示出∠MBC与∠BCN,再根据角平分线的性质可求得∠CBQ+∠BCQ,最后根据三角形内角和定理即可求解;
(3)在△BQE中,由于∠Q=90°∠A,求出∠E=∠A,∠EBQ=90°,所以如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况进行讨论:①∠EBQ=2∠E=90°;②∠EBQ=2∠Q=90°;③∠Q=2∠E;④∠E=2∠Q;分别列出方程,求解即可.
【详解】(1)∵,
∴,
又∵点是和的平分线的交点,
∴,
∴;
(2)∵外角,的角平分线交于点,
∴,,
∵,,
∴,,
∴
,
∴
;
(3)延长BC至F,
∵CQ为△ABC的外角∠NCB的角平分线,
∴CE是△ABC的外角∠ACF的平分线,
∴∠ACF=2∠ECF,
∵BE平分∠ABC,
∴∠ABC=2∠EBC,
∵∠ECF=∠EBC+∠E,
∴2∠ECF=2∠EBC+2∠E,
即∠ACF=∠ABC+2∠E,
又∵∠ACF=∠ABC+∠A,
∴∠A=2∠E,即∠E=∠A,
∵∠EBQ=∠EBC+∠CBQ
=∠ABC+∠MBC
=(∠ABC+∠A+∠ACB)
=90°.
如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况:
①∠EBQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;
②∠EBQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;
③∠Q=2∠E,则∠E=30°,解得∠A=2∠E=60°;
④∠E=2∠Q,则∠E=60°,解得∠A=2∠E=120°.
综上所述,∠A的度数是90°或60°或120°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级上册数学 11.2.2三角形的外角 同步练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.三角形的一个外角,不大于和它相邻的内角,这个三角形一定是
A.锐角三角形 B.直角三角形
C.钝角三角形 D.非锐角三角形
2.下列叙述中正确的是
A.三角形的外角等于两个内角的和
B.三角形的外角大于内角
C.三角形的外角等于与它不相邻的两个内角和
D.三角形每一个内角都只有一个外角
3.一副三角板有两个直角三角形,如图叠放在一起,则∠α的度数是
A.165° B.120° C.150° D.135°
4.如图,把纸片沿DE折叠,点A落在四边形BCED的外部,,,则的度数为( )
A.32° B.30° C.28° D.26°
5.如图,,点在上,,,则下列结论正确的个数是( )
(1);(2);(3);(4)
A.1个 B.2个 C.3个 D.4个
6.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
A.105° B.95° C.85° D.75°
7.如图,在△ABC中,∠ACB=90°,D在AB上,将△ABC沿CD折叠,点B落在AC边上的点B′处,若,则∠A的度数为( )
A.25° B.30° C.35° D.40°
8.如图,和相交于点,,则下列结论中不正确的是( ).
A. B.
C. D.
9.已知,是的边上一点,,和的平分线交于点,若,则的大小为( )
A. B. C. D.
10.下列命题是假命题的是( )
A.三角形的内角和是180° B.两直线平行,内错角相等
C.三角形的外角大于任何一个内角 D.同旁内角互补,两直线平行
填空题(本大题共5小题,每小题4分,共20分。)
11.如图,在△ABC中,∠B=66°,∠C=54°,AD是∠BAC的平分线,DE平分∠ADC交AC于E,则∠ADE=
__________.
12.已知,直线交于点,交于点是直线上一动点,过作直线的垂线交于点.若,则__________.
13.如图,在△ABC中,BD平分∠ABC,连接CD,若∠A=∠D=40°,∠ACD=30°,则∠DCE的度数为_____.
14.如图,,点,分别在射线,上,平分,的反向延长线与的平分线交于点,则的度数是_______.
15.已知,一个含角的直角三角板按如图所示放置,,则_____.
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.已知,如图,点D是中AC边上的一点,点E是BC边延长线上一点,说明:.
17.如图,在△ABC中,D是BC上的一点,∠1=∠2,∠3=∠4,∠B=40°,求∠BAC的度数.
18.如图,在中,,直线分别交的边、和的延长线于点、、.
(1)若,则__________.
(2)、、有什么数量关系?请说明理由.
19.将△ABC纸片沿DE折叠,其中∠B=∠C.
(1)如图1,点C落在BC边上的点F处,AB与DF是否平行?请说明理由;
(2)如图2,点C落在四边形ABCD内部的点G处,探索∠B与∠1+∠2之间的数量关系,并说明理由.
20.在中,与的平分线相交于点.
(1)如图①,如果,求的度数;
(2)如图②,作外角,的角平分线,且交于点,试探索,之间的数量关系;
(3)如图③,在图②中延长线段,交于点若中存在一个内角等于另一个内角的2倍,求的度数.
参考答案
选择题
1.【答案】D
【解析】因为三角形的一个外角与它相邻的内角和为180°,而题中说这个外角不大于它相邻的内角,所以可知与它相邻的这个内角是一个大于或等于90°的角,则这个三角形就是一个钝角三角形或直角三角形.故选D.
2.【答案】C
【解析】A、三角形的外角等于和它不相邻的两个内角的和,故本选项错误;
B、三角形的外角大于和它不相邻的一个内角,故本选项错误.
C、符合三角形外角的性质,故本选项正确;
D、三角形每一个内角都有两个外角,故本选项错误.故选C.
3.【答案】A
【解析】如图,
∵∠2=90°-30°=60°,∴∠1=∠2-45°=15°,∴∠α=180°-∠1=165°.故选A.
4.【答案】C
【分析】根据翻折的性质可得,再利用三角形外角的性质表示出,然后根据角的和差整理即可得解.
【详解】解:如图,由翻折的性质得,
∴,
∴在△ADE中,,
∵,
∴,
∴,
∵,,
∴.
故选:C.
5.【答案】B
【分析】利用平行线的性质和三角形的性质依次判断即可求解.
【详解】解:∵AB∥CD,
∴∠A+∠C=180°,
又∵∠A=110°,
∴∠C=70°,
∴∠AED=∠C+∠D=85°,故(2)正确,
∵∠C+∠D+∠CED=180°,
∴∠D+∠CED=110°,
∴∠A=∠CED+∠D,故(3)正确,
∵点E在AC上的任意一点,
∴AE无法判断等于CE,∠BED无法判断等于45°,故(1)、(4)错误,
故选:B.
6.【答案】C
【分析】根据角平分线的性质,求得∠ACD=120°,利用三角形的外角性质求解即可.
【详解】∵CE是△ABC的外角∠ACD的平分线,∠ACE=60°,
∴∠ACD=120°,
∵∠ACD=∠A+∠B,且∠B=35°,
∴∠A=85°,
故选C.
7.【答案】C
【分析】利用翻折不变性,三角形内角和定理和三角形外角的性质即可解决问题.
【详解】∵∠ACB=90°,
∴∠A+∠B=90°,
∵△CDB′是由△CDB翻折得到,
∴∠CB′D=∠B,
∵∠CB′D=∠A+∠ADB′=∠A+20°,
∴∠A+∠A+20°=90°,
解得∠A=35°.
故选:C.
8.【答案】D
【分析】利用三角形的外角性质,对顶角相等逐一判断即可.
【详解】∵∠1=∠2,∠A=∠C,∠1=∠A+∠D,∠2=∠B+∠C,
∴∠B=∠D,
∴选项A、B正确;
∵∠2=∠A+∠D,
∴,
∴选项C正确;
没有条件说明
故选:D.
9.【答案】C
【分析】先利用角平分线和三角形外角的性质可得,再根据平行线的性质定理即可得出的大小.
【详解】解:如下图所示,
∵和的平分线交于点,
∴,
∵,,
∴,
∵,
∴,
∵,
∴,
故选:C.
10.【答案】C
【分析】根据三角形内角和定理、外角性质、平行线的性质与判定进行判断即可.
【详解】解:A选项,三角形的内角和是180°,是真命题,不符合题意;
B选项,两直线平行,内错角相等,是真命题,不符合题意;
C选项,三角形的外角大于任何一个内角,是假命题,符合题意;
D选项,同旁内角互补,两直线平行,是真命题,不符合题意;
故选:C.
填空题
11.【答案】48°
12.【答案】90°或30°
【分析】先由两直线平行,内错角相等得出∠EFC=∠PEF.若设∠PEF=x,则∠EFC=x,∠APQ=2x,∠EQP=x,再由EF⊥PQ,根据三角形内角和定理得到∠PEF+∠APQ=90°,即x+2x=90°,解方程求出x=30°,然后根据三角形外角的性质即可求出∠AEQ的度数.
【详解】解:①如图:
∵AB∥CD,
∴∠EFC=∠PEF.
设∠PEF=x,则∠EFC=x,∠APQ=2∠EFC=2x,∠EQP=∠EFC=x.
∵EF⊥PQ,
∴∠PEF+∠APQ=90°,即x+2x=90°,
解得x=30°,
∴∠EQP=x=30°,∠APQ=2x=60°,
∴∠AEQ=∠EQP+∠APQ=30°+60°=90°.
②如图:
易知∠EFC=∠FEB=∠HEA,∠APQ=∠HPE,
又∵∠PHE=90°,
故∠EFC=30°,∠EQP=30°,∠APQ=60°;
故∠AEQ=∠APQ ∠EQP=30°.
综上所述:90°或30°.
故答案是:90°或30°.
13.【答案】70°.
【分析】由三角形的外角的性质定理得到∠ACE=∠A+∠ABC,∠DCE=∠CBD+∠D,再由已知∠ABD=∠CBD,∠A=∠D=40°,∠ACD=30°解方程组可求得结果.
【详解】∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵∠ACE=∠A+∠ABC=40°+2∠CBD,
∴∠DCE+∠ACD=∠A+2∠CBD,
∵∠DCE=∠CBD+∠D,∠A=∠D=40°,∠ACD=30°,
∴∠DCE+30°=40°+2∠CBD,即∠DCE=2∠CBD+10°①,
∠DCE=40°+∠CBD②,
由①②得∠DCE=70°,
故答案为:70°.
14.【答案】
【分析】根据三角形的一个外角等于与它不相邻的两个内角的和,列式求出,再根据角平分线的定义求出和,然后根据三角形的一个外角等于与它不相邻的两个内角的和,列式计算即可得解.
【详解】解:根据三角形的外角性质,可得,
平分,平分,
,,
,
,
,
,
,
,
.
故答案为:45°.
15.【答案】75°.
【分析】利用外角求∠5,再根据平行线的性质求∠1.
【详解】解:由题意可知∠4=45°,∠2=∠3=30°,
∠5=∠2+∠3=75°,
∵,
∴∠1=∠5=75°,
故答案为:75°.
解答题
16.【解析】∵∠DCB是△DCE的一个外角,∴∠DCB>∠CDE.
∵∠ADB是△BCD的一个外角,
∴∠ADB>∠DCB,
∴∠ADB>∠CDE.
17.【解析】∵∠1=∠2,∠B=40°,
∴∠2=∠1=(180°-40°)÷2=70°,
又∵∠2是△ADC的外角,∴∠2=∠3+∠4,
∵∠3=∠4,∴∠2=2∠3,
∴∠3=∠2=35°,
∴∠BAC=∠1+∠3=105°.
18.【答案】(1);(2)∠F+∠FEC=2∠A,理由见解析
【分析】(1)在△ABC中,利用三角形内角和定理求得∠C的度数,再在△EFC中,利用三角形内角和定理即可求解;
(2)根据三角形外角的性质,可得出∠FEC=∠A+∠ADE,∠F+∠BDF=∠ABC,再根据∠A=∠ABC,即可得出答案.
【详解】(1)在△ABC中,∠A=∠ABC,且∠A=70°,
∴∠C=,
∴∠F+∠FEC=;
故答案为:;
(2)∠F+∠FEC=2∠A,
理由:∵∠FEC=∠A+∠ADE,∠F+∠BDF=∠ABC,
∴∠F+∠FEC=∠F+∠A+∠ADE,
∵∠ADE=∠BDF,
∴∠F+∠FEC=∠A+∠ABC,
∵∠A=∠ABC,
∴∠F+∠FEC=∠A+∠ABC=2∠A.
19.【答案】(1)平行,理由见解析;(2)∠1+∠2=2∠B,理由见解析
【分析】(1)AB与DF平行.根据翻折可得出∠DFC=∠C,结合∠B=∠C即可得出∠B=∠DFC,从而证出AB∥DF;
(2)连接GC,由翻折可得出∠DGE=∠ACB,再根据三角形外角的性质得出∠1=∠DGC+∠DCG,∠2=∠EGC+∠ECG,通过角的运算即可得出∠1+∠2=2∠B.
【详解】解:(1)AB与DF平行.理由如下:
由翻折,得∠DFC=∠C.
又∵∠B=∠C,
∴∠B=∠DFC,
∴AB∥DF.
(2)连接GC,如图所示.
由翻折,得∠DGE=∠ACB.
∵∠1=∠DGC+∠DCG,∠2=∠EGC+∠ECG,
∴∠1+∠2=∠DGC+∠DCG+∠EGC+∠ECG=(∠DGC+∠EGC)+(∠DCG+∠ECG)=∠DGE+∠DCE=2∠ACB.
∵∠B=∠ACB,
∴∠1+∠2=2∠B.
20.【答案】(1);(2);(3)的度数是90°或60°或120°
【分析】(1)运用三角形的内角和定理及角平分线的定义,首先求出∠PBC+∠PCB,进而求出∠BPC即可解决问题;
(2)根据三角形的外角性质分别表示出∠MBC与∠BCN,再根据角平分线的性质可求得∠CBQ+∠BCQ,最后根据三角形内角和定理即可求解;
(3)在△BQE中,由于∠Q=90°∠A,求出∠E=∠A,∠EBQ=90°,所以如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况进行讨论:①∠EBQ=2∠E=90°;②∠EBQ=2∠Q=90°;③∠Q=2∠E;④∠E=2∠Q;分别列出方程,求解即可.
【详解】(1)∵,
∴,
又∵点是和的平分线的交点,
∴,
∴;
(2)∵外角,的角平分线交于点,
∴,,
∵,,
∴,,
∴
,
∴
;
(3)延长BC至F,
∵CQ为△ABC的外角∠NCB的角平分线,
∴CE是△ABC的外角∠ACF的平分线,
∴∠ACF=2∠ECF,
∵BE平分∠ABC,
∴∠ABC=2∠EBC,
∵∠ECF=∠EBC+∠E,
∴2∠ECF=2∠EBC+2∠E,
即∠ACF=∠ABC+2∠E,
又∵∠ACF=∠ABC+∠A,
∴∠A=2∠E,即∠E=∠A,
∵∠EBQ=∠EBC+∠CBQ
=∠ABC+∠MBC
=(∠ABC+∠A+∠ACB)
=90°.
如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况:
①∠EBQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;
②∠EBQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;
③∠Q=2∠E,则∠E=30°,解得∠A=2∠E=60°;
④∠E=2∠Q,则∠E=60°,解得∠A=2∠E=120°.
综上所述,∠A的度数是90°或60°或120°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
