人教版高中数学选择性必修第三册7.3.2离散型随机变量的方差 课件(共51张PPT)
文档属性
| 名称 | 人教版高中数学选择性必修第三册7.3.2离散型随机变量的方差 课件(共51张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-15 00:00:00 | ||
图片预览











文档简介
(共51张PPT)
第七章 随机变量及其分布
7.3.2 离散型随机变量的方差
7.3 离散型随机变量的数字特征
课标要求
1.通过具体实例,理解离散型随机变量的分布列及方差的概念.2.能计算简单离散型随机变量的方差,并能解决一些实际问题.
素养要求
通过研究离散型随机变量的方差,发展数学抽象及数据分析素养.
问题导学预习教材 必备知识探究
1
1.问题 从两名同学中挑出一名代表班级参加射击比赛.根据以往的成绩记录,第一名同学击中目标靶的环数X1的分布列为
X1 5 6 7 8 9 10
P 0.03 0.09 0.20 0.31 0.27 0.10
第二名同学击中目标靶的环数X2的分布列为
X2 5 6 7 8 9
P 0.01 0.05 0.20 0.41 0.33
(1)能否根据X1和X2的均值来决定派哪名同学参赛?
提示 E(X1)=8,E(X2)=8,均值相等.不能根据X1和X2的均值决定选派人员.
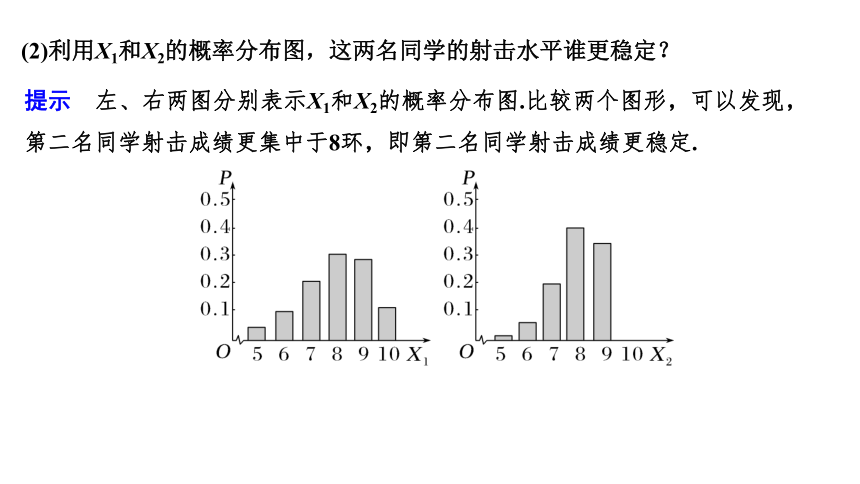
提示 左、右两图分别表示X1和X2的概率分布图.比较两个图形,可以发现,第二名同学射击成绩更集中于8环,即第二名同学射击成绩更稳定.
(2)利用X1和X2的概率分布图,这两名同学的射击水平谁更稳定?
(3)怎样定量刻画随机变量的稳定性?
提示 样本方差反映了样本数据与样本均值的偏离程度,可刻画样本数据的稳定性.因此随机变量的方差和标准差可刻画随机变量的稳定性.
2.填空 (1)设离散型随机变量X的分布列为
X x1 x2 … xi … xn
P p1 p2 … pi … pn
(x1-E(X))2p1+(x2-E(X))2p2+…+(xn-E(X))2pn
标准差
(2)随机变量的方差和标准差都可以度量随机变量取值与其均值的偏离程度,反映了随机变量取值的离散程度.方差或标准差越小,随机变量的取值越______;方差或标准差越大,随机变量的取值越______.
集中
分散
(3)几个常见的结论
①D(aX+b)=________.
②若X服从两点分布,则D(X)=_________.
a2D(X)
p(1-p)
B
3.做一做 (1)已知随机变量X的分布列为
X -1 0 1
P 0.5 0.3 0.2
则D(X)等于( )
A.0.7 B.0.61
C.-0.3 D.0
解析 E(X)=-1×0.5+0×0.3+1×0.2=-0.3,
∴D(X)=(-1+0.3)2×0.5+(0+0.3)2×0.3+(1+0.3)2×0.2=0.61.
4
(2)设随机变量X的方差D(X)=1,则D(2X+1)的值为________.
解析 D(2X+1)=22D(X)=4×1=4.
(1)离散型随机变量的方差越大, 随机变量越稳定.( )
提示 随机变量的方差越小,随机变量越稳定.
(2)若a是常数, 则D(a)=0.( )
(3)离散型随机变量的方差反映了随机变量偏离于期望的平均程度.( )
(4)若随机变量X服从两点分布, 且成功的概率p=0.5, 则D(X)=0.25.( )
×
4.思考辨析 正确的在后面的括号内画“√”,错误的画“×”.
√
√
√
HU DONG HE ZUO YAN XI TI XING GUAN JIAN NENG LI TI SHENG
互动合作研析题型 关键能力提升
2
例1 有10张卡片,其中8张标有数字2,2张标有数字5,从中随机地抽取3张卡片,设3张卡片数字之和为ξ,求E(ξ)和D(ξ).
题型一 求离散型随机变量的方差
解 这3张卡片上的数字之和为ξ,ξ的可能取值为6,9,12.
ξ=6表示取出的3张卡片上均标有2,
ξ=9表示取出的3张卡片上两张标有2,一张标有5,
ξ=12表示取出的3张卡片上一张标有2,两张标有5,
因此随机变量ξ的分布列为
求离散型随机变量的步骤
(1)明确随机变量的所有可能取值,并理解每一个取值的意义.
(2)求出随机变量取各个值的概率.
(3)列出随机变量的分布列.
(4)由分布列计算E(X),进而求随机变量的方差D(X).
思维升华
解 乙投篮的次数ξ的可能取值为0,1,2.
故ξ的分布列为
例2 已知离散型随机变量X的分布列为
题型二 方差的性质的应用
∴x=2.
解 ∵Y=3X-2,
∴D(Y)=D(3X-2)=9D(X)=5,
求随机变量Y=aX+b方差的方法
求随机变量Y=aX+b的方差,一种方法是先求Y的分布列,再求其均值,最后求方差;另一种方法是应用公式D(aX+b)=a2D(X)求解.
思维升华
训练2 (多选)若随机变量X的分布列为
CD
X 0 1
P 0.2 m
已知随机变量Y=aX+b(a,b∈R)且E(Y)=10,D(Y)=4,则a与b的值可以分别为( )
A.a=10,b=3 B.a=3,b=10
C.a=5,b=6 D.a=-5,b=14
解析 因为0.2+m=1,所以m=0.8,
由两点分布,知E(X)=0.8,D(X)=0.8×0.2=0.16.
因为Y=aX+b(a,b∈R),E(Y)=10,D(Y)=4,
所以aE(X)+b=0.8a+b=10,a2D(X)=0.16a2=4,
解之得a=5,b=6或a=-5,b=14.
题型三 方差的简单应用
例3 有甲、乙两种建筑材料,从中各取等量样品检查它们的抗拉强度如下:
其中,XA,XB分别表示甲、乙两种材料的抗拉强度,在使用时要求抗拉强度不低于120,试比较甲、乙两种建筑材料的稳定程度(哪一个的稳定性较好).
解 E(XA)=110×0.1+120×0.2+125×0.4+130×0.1+135×0.2=125,
E(XB)=100×0.1+115×0.2+125×0.4+130×0.1+145×0.2=125,
D(XA)=0.1×(110-125)2+0.2×(120-125)2+0.4×(125-125)2+0.1×(130-125)2+0.2×(135-125)2=50,
D(XB)=0.1×(100-125)2+0.2×(115-125)2+0.4×(125-125)2+0.1×(130-125)2+0.2×(145-125)2=165.
由此可见E(XA)=E(XB),D(XA)<D(XB),
故两种材料的抗拉强度的平均值相等,其稳定程度材料乙明显不如材料甲,即甲的稳定性好.
(1)均值体现了随机变量取值的平均大小,在两种产品相比较时,只比较均值往往是不恰当的,还需比较它们的取值的离散程度,即通过比较方差,才能准确地得出更恰当的判断.
(2)离散型随机变量的分布列、均值、方差之间存在着紧密的联系,利用题目中所给出的条件,合理地列出方程或方程组求解,同时也应注意合理选择公式,简化问题的解答过程.
思维升华
训练3 甲、乙两名射手在一次射击中得分为两个相互独立的随机变量ξ与η,且ξ,η的分布列为
ξ 1 2 3
P a 0.1 0.6
η 1 2 3
P 0.3 b 0.3
(1)求a,b的值;
解 由离散型随机变量的分布列的性质可知a+0.1+0.6=1,∴a=0.3.
同理0.3+b+0.3=1,∴b=0.4.
(2)计算ξ,η的均值与方差,并以此分析甲、乙的技术状况.
解 E(ξ)=1×0.3+2×0.1+3×0.6=2.3,
E(η)=1×0.3+2×0.4+3×0.3=2,
D(ξ)=(1-2.3)2×0.3+(2-2.3)2×0.1+(3-2.3)2×0.6=0.81,
D(η)=(1-2)2×0.3+(2-2)2×0.4+(3-2)2×0.3=0.6.
由于E(ξ)>E(η),说明在一次射击中,甲的平均得分比乙高,
但D(ξ)>D(η),说明甲得分的稳定性不如乙,
因此甲、乙两人技术水平都不够全面,各有优劣.
课堂小结
1.(1)求离散型随机变量的方差步骤关键在于:①准确求出随机变量的分布列;②计算均值E(X);③利用定义或公式D(X)=E(X2)-[E(X)]2计算.
(2)灵活利用方差的性质D(aX+b)=a2D(X)简化计算.
2.解题的常见误区:方差与标准差均反映随机变量的稳定程度,但有区别,标准差的单位与随机变量取值的单位相同,但方差则不同.
TUO ZHAN YAN SHEN FEN CENG JING LIAN HE XIN SU YANG DA CHENG
拓展延伸分层精练 核心素养达成
3
A.m B.2m(1-m)
C.m(m-1) D.m(1-m)
D
解析 由题意知X服从两点分布,故D(X)=m(1-m).
A.6 B.8 C.3 D.4
B
∴D(2X-5)=4D(X)=4×2=8.
3.设0D
则当p在(0,1)内增大时,( )
A.D(ξ)减小 B.D(ξ)增大
C.D(ξ)先减小后增大 D.D(ξ)先增大后减小
解析 由分布列可知
4.以往的统计资料表明,甲、乙两运动员在比赛中得分情况为
A
现有一场比赛,派哪位运动员参加较好?( )
A.甲 B.乙
C.甲、乙均可 D.无法确定
解析 E(X1)=0×0.2+1×0.5+2×0.3=1.1,
E(X2)=0×0.3+1×0.3+2×0.4=1.1,
D(X1)=1.12×0.2+0.12×0.5+0.92×0.3=0.49,
D(X2)=1.12×0.3+0.12×0.3+0.92×0.4=0.69.
∴E(X1)=E(X2),D(X1)即甲比乙得分稳定,选甲参加较好.
5.(多选)已知离散型随机变量X的分布列为
AC
则下列式子正确的是( )
6.若某事件在一次试验中发生次数的方差等于0.25,则该事件在一次试验中发生的概率为__________.
0.5
解析 设该事件在一次试验中发生的概率为p,该事件在一次试验中发生次数记为X,
则X服从两点分布,则D(X)=p(1-p),
所以p(1-p)=0.25,解得p=0.5.
7.设随机变量X的分布列为
2
若Y=2X+2,则D(Y)=________.
8.已知离散型随机变量X的分布列为
0.49
且E(X)=1.1,则D(X)=__________.
解得x=2.
9.已知η的分布列为
(1)求η的方差;
(2)设Y=2η-E(η),求D(Y).
解 ∵Y=2η-E(η),
∴D(Y)=D[2η-E(η)]
=22D(η)=4×384=1 536.
10.已知海关大楼顶端镶有A,B两面大钟,它们的日走时误差分别为X1,X2(单位:s),其分布列如下:
根据这两面大钟日走时误差的均值与方差比较这两面大钟的质量.
解 由题意得,E(X1)=0,E(X2)=0,
∴E(X1)=E(X2).
D(X1)=(-2-0)2×0.05+(-1-0)2×0.05+(0-0)2×0.8+(1-0)2×0.05+(2-0)2×0.05=0.5,
D(X2)=(-2-0)2×0.1+(-1-0)2×0.2+(0-0)2×0.4+(1-0)2×0.2+(2-0)2×0.1=1.2.
∴D(X1)综上可知,A大钟的质量较好.
11.(多选)设离散型随机变量X的分布列为
AC
若离散型随机变量Y满足Y=2X+1,则下列结果正确的有( )
A.E(X)=2 B.D(X)=2.4 C.D(X)=2.8 D.D(Y)=14
解析 由离散型随机变量X的分布列的性质,得q=1-0.3-0.2-0.2-0.1=0.2,
则E(X)=0×0.2+1×0.3+2×0.2+4×0.2+5×0.1=2,
D(X)=(0-2)2×0.2+(1-2)2×0.3+(2-2)2×0.2+(4-2)2×0.2+(5-2)2×0.1=2.8.
∵Y=2X+1,
∴D(Y)=22D(X)=4D(X)=4×2.8=11.2.
12.两封信随机投入A,B,C三个空邮箱中,则A邮箱的信件数X的方差D(X)=________.
解析 X的所有可能取值为0,1,2,
13.某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分为n小块地,在总共2n小块地中,随机选n小块地种植品种甲,另外n小块地种植品种乙.假设n=4,在第一大块地中,种植品种甲的小块地的数目记为X,求X的分布列、均值及方差.
解 X可能的取值为0,1,2,3,4,
即X的分布列为
14.根据以往的经验,某工程施工期间的降水量X(单位:mm)对工期的影响如下表所示.
3
降水量X X<300 300≤X<700 700≤X<900 X≥900
工期延误天数Y 0 2 6 10
若历史气象资料表明,该工程施工期间降水量X小于300,700,900的概率分别为0.3,0.7,0.9,则工期延误天数Y的期望是________,工期延误天数Y的方差为________.
9.8
解析 由已知条件和概率的加法公式知,
P(X<300)=0.3,
P(300≤X<700)=P(X<700)-P(X<300)=0.7-0.3=0.4,
P(700≤X<900)=P(X<900)-P(X<700)=0.9-0.7=0.2,
P(X≥900)=1-P(X<900)=1-0.9=0.1.
所以随机变量Y的分布列为
Y 0 2 6 10
P 0.3 0.4 0.2 0.1
故E(Y)=0×0.3+2×0.4+6×0.2+10×0.1=3(天),
D(Y)=(0-3)2×0.3+(2-3)2×0.4+(6-3)2×0.2+(10-3)2×0.1=9.8.
故工期延误天数Y的方差为9.8.
本课结束
本课结束
第七章 随机变量及其分布
7.3.2 离散型随机变量的方差
7.3 离散型随机变量的数字特征
课标要求
1.通过具体实例,理解离散型随机变量的分布列及方差的概念.2.能计算简单离散型随机变量的方差,并能解决一些实际问题.
素养要求
通过研究离散型随机变量的方差,发展数学抽象及数据分析素养.
问题导学预习教材 必备知识探究
1
1.问题 从两名同学中挑出一名代表班级参加射击比赛.根据以往的成绩记录,第一名同学击中目标靶的环数X1的分布列为
X1 5 6 7 8 9 10
P 0.03 0.09 0.20 0.31 0.27 0.10
第二名同学击中目标靶的环数X2的分布列为
X2 5 6 7 8 9
P 0.01 0.05 0.20 0.41 0.33
(1)能否根据X1和X2的均值来决定派哪名同学参赛?
提示 E(X1)=8,E(X2)=8,均值相等.不能根据X1和X2的均值决定选派人员.
提示 左、右两图分别表示X1和X2的概率分布图.比较两个图形,可以发现,第二名同学射击成绩更集中于8环,即第二名同学射击成绩更稳定.
(2)利用X1和X2的概率分布图,这两名同学的射击水平谁更稳定?
(3)怎样定量刻画随机变量的稳定性?
提示 样本方差反映了样本数据与样本均值的偏离程度,可刻画样本数据的稳定性.因此随机变量的方差和标准差可刻画随机变量的稳定性.
2.填空 (1)设离散型随机变量X的分布列为
X x1 x2 … xi … xn
P p1 p2 … pi … pn
(x1-E(X))2p1+(x2-E(X))2p2+…+(xn-E(X))2pn
标准差
(2)随机变量的方差和标准差都可以度量随机变量取值与其均值的偏离程度,反映了随机变量取值的离散程度.方差或标准差越小,随机变量的取值越______;方差或标准差越大,随机变量的取值越______.
集中
分散
(3)几个常见的结论
①D(aX+b)=________.
②若X服从两点分布,则D(X)=_________.
a2D(X)
p(1-p)
B
3.做一做 (1)已知随机变量X的分布列为
X -1 0 1
P 0.5 0.3 0.2
则D(X)等于( )
A.0.7 B.0.61
C.-0.3 D.0
解析 E(X)=-1×0.5+0×0.3+1×0.2=-0.3,
∴D(X)=(-1+0.3)2×0.5+(0+0.3)2×0.3+(1+0.3)2×0.2=0.61.
4
(2)设随机变量X的方差D(X)=1,则D(2X+1)的值为________.
解析 D(2X+1)=22D(X)=4×1=4.
(1)离散型随机变量的方差越大, 随机变量越稳定.( )
提示 随机变量的方差越小,随机变量越稳定.
(2)若a是常数, 则D(a)=0.( )
(3)离散型随机变量的方差反映了随机变量偏离于期望的平均程度.( )
(4)若随机变量X服从两点分布, 且成功的概率p=0.5, 则D(X)=0.25.( )
×
4.思考辨析 正确的在后面的括号内画“√”,错误的画“×”.
√
√
√
HU DONG HE ZUO YAN XI TI XING GUAN JIAN NENG LI TI SHENG
互动合作研析题型 关键能力提升
2
例1 有10张卡片,其中8张标有数字2,2张标有数字5,从中随机地抽取3张卡片,设3张卡片数字之和为ξ,求E(ξ)和D(ξ).
题型一 求离散型随机变量的方差
解 这3张卡片上的数字之和为ξ,ξ的可能取值为6,9,12.
ξ=6表示取出的3张卡片上均标有2,
ξ=9表示取出的3张卡片上两张标有2,一张标有5,
ξ=12表示取出的3张卡片上一张标有2,两张标有5,
因此随机变量ξ的分布列为
求离散型随机变量的步骤
(1)明确随机变量的所有可能取值,并理解每一个取值的意义.
(2)求出随机变量取各个值的概率.
(3)列出随机变量的分布列.
(4)由分布列计算E(X),进而求随机变量的方差D(X).
思维升华
解 乙投篮的次数ξ的可能取值为0,1,2.
故ξ的分布列为
例2 已知离散型随机变量X的分布列为
题型二 方差的性质的应用
∴x=2.
解 ∵Y=3X-2,
∴D(Y)=D(3X-2)=9D(X)=5,
求随机变量Y=aX+b方差的方法
求随机变量Y=aX+b的方差,一种方法是先求Y的分布列,再求其均值,最后求方差;另一种方法是应用公式D(aX+b)=a2D(X)求解.
思维升华
训练2 (多选)若随机变量X的分布列为
CD
X 0 1
P 0.2 m
已知随机变量Y=aX+b(a,b∈R)且E(Y)=10,D(Y)=4,则a与b的值可以分别为( )
A.a=10,b=3 B.a=3,b=10
C.a=5,b=6 D.a=-5,b=14
解析 因为0.2+m=1,所以m=0.8,
由两点分布,知E(X)=0.8,D(X)=0.8×0.2=0.16.
因为Y=aX+b(a,b∈R),E(Y)=10,D(Y)=4,
所以aE(X)+b=0.8a+b=10,a2D(X)=0.16a2=4,
解之得a=5,b=6或a=-5,b=14.
题型三 方差的简单应用
例3 有甲、乙两种建筑材料,从中各取等量样品检查它们的抗拉强度如下:
其中,XA,XB分别表示甲、乙两种材料的抗拉强度,在使用时要求抗拉强度不低于120,试比较甲、乙两种建筑材料的稳定程度(哪一个的稳定性较好).
解 E(XA)=110×0.1+120×0.2+125×0.4+130×0.1+135×0.2=125,
E(XB)=100×0.1+115×0.2+125×0.4+130×0.1+145×0.2=125,
D(XA)=0.1×(110-125)2+0.2×(120-125)2+0.4×(125-125)2+0.1×(130-125)2+0.2×(135-125)2=50,
D(XB)=0.1×(100-125)2+0.2×(115-125)2+0.4×(125-125)2+0.1×(130-125)2+0.2×(145-125)2=165.
由此可见E(XA)=E(XB),D(XA)<D(XB),
故两种材料的抗拉强度的平均值相等,其稳定程度材料乙明显不如材料甲,即甲的稳定性好.
(1)均值体现了随机变量取值的平均大小,在两种产品相比较时,只比较均值往往是不恰当的,还需比较它们的取值的离散程度,即通过比较方差,才能准确地得出更恰当的判断.
(2)离散型随机变量的分布列、均值、方差之间存在着紧密的联系,利用题目中所给出的条件,合理地列出方程或方程组求解,同时也应注意合理选择公式,简化问题的解答过程.
思维升华
训练3 甲、乙两名射手在一次射击中得分为两个相互独立的随机变量ξ与η,且ξ,η的分布列为
ξ 1 2 3
P a 0.1 0.6
η 1 2 3
P 0.3 b 0.3
(1)求a,b的值;
解 由离散型随机变量的分布列的性质可知a+0.1+0.6=1,∴a=0.3.
同理0.3+b+0.3=1,∴b=0.4.
(2)计算ξ,η的均值与方差,并以此分析甲、乙的技术状况.
解 E(ξ)=1×0.3+2×0.1+3×0.6=2.3,
E(η)=1×0.3+2×0.4+3×0.3=2,
D(ξ)=(1-2.3)2×0.3+(2-2.3)2×0.1+(3-2.3)2×0.6=0.81,
D(η)=(1-2)2×0.3+(2-2)2×0.4+(3-2)2×0.3=0.6.
由于E(ξ)>E(η),说明在一次射击中,甲的平均得分比乙高,
但D(ξ)>D(η),说明甲得分的稳定性不如乙,
因此甲、乙两人技术水平都不够全面,各有优劣.
课堂小结
1.(1)求离散型随机变量的方差步骤关键在于:①准确求出随机变量的分布列;②计算均值E(X);③利用定义或公式D(X)=E(X2)-[E(X)]2计算.
(2)灵活利用方差的性质D(aX+b)=a2D(X)简化计算.
2.解题的常见误区:方差与标准差均反映随机变量的稳定程度,但有区别,标准差的单位与随机变量取值的单位相同,但方差则不同.
TUO ZHAN YAN SHEN FEN CENG JING LIAN HE XIN SU YANG DA CHENG
拓展延伸分层精练 核心素养达成
3
A.m B.2m(1-m)
C.m(m-1) D.m(1-m)
D
解析 由题意知X服从两点分布,故D(X)=m(1-m).
A.6 B.8 C.3 D.4
B
∴D(2X-5)=4D(X)=4×2=8.
3.设0
则当p在(0,1)内增大时,( )
A.D(ξ)减小 B.D(ξ)增大
C.D(ξ)先减小后增大 D.D(ξ)先增大后减小
解析 由分布列可知
4.以往的统计资料表明,甲、乙两运动员在比赛中得分情况为
A
现有一场比赛,派哪位运动员参加较好?( )
A.甲 B.乙
C.甲、乙均可 D.无法确定
解析 E(X1)=0×0.2+1×0.5+2×0.3=1.1,
E(X2)=0×0.3+1×0.3+2×0.4=1.1,
D(X1)=1.12×0.2+0.12×0.5+0.92×0.3=0.49,
D(X2)=1.12×0.3+0.12×0.3+0.92×0.4=0.69.
∴E(X1)=E(X2),D(X1)
5.(多选)已知离散型随机变量X的分布列为
AC
则下列式子正确的是( )
6.若某事件在一次试验中发生次数的方差等于0.25,则该事件在一次试验中发生的概率为__________.
0.5
解析 设该事件在一次试验中发生的概率为p,该事件在一次试验中发生次数记为X,
则X服从两点分布,则D(X)=p(1-p),
所以p(1-p)=0.25,解得p=0.5.
7.设随机变量X的分布列为
2
若Y=2X+2,则D(Y)=________.
8.已知离散型随机变量X的分布列为
0.49
且E(X)=1.1,则D(X)=__________.
解得x=2.
9.已知η的分布列为
(1)求η的方差;
(2)设Y=2η-E(η),求D(Y).
解 ∵Y=2η-E(η),
∴D(Y)=D[2η-E(η)]
=22D(η)=4×384=1 536.
10.已知海关大楼顶端镶有A,B两面大钟,它们的日走时误差分别为X1,X2(单位:s),其分布列如下:
根据这两面大钟日走时误差的均值与方差比较这两面大钟的质量.
解 由题意得,E(X1)=0,E(X2)=0,
∴E(X1)=E(X2).
D(X1)=(-2-0)2×0.05+(-1-0)2×0.05+(0-0)2×0.8+(1-0)2×0.05+(2-0)2×0.05=0.5,
D(X2)=(-2-0)2×0.1+(-1-0)2×0.2+(0-0)2×0.4+(1-0)2×0.2+(2-0)2×0.1=1.2.
∴D(X1)
11.(多选)设离散型随机变量X的分布列为
AC
若离散型随机变量Y满足Y=2X+1,则下列结果正确的有( )
A.E(X)=2 B.D(X)=2.4 C.D(X)=2.8 D.D(Y)=14
解析 由离散型随机变量X的分布列的性质,得q=1-0.3-0.2-0.2-0.1=0.2,
则E(X)=0×0.2+1×0.3+2×0.2+4×0.2+5×0.1=2,
D(X)=(0-2)2×0.2+(1-2)2×0.3+(2-2)2×0.2+(4-2)2×0.2+(5-2)2×0.1=2.8.
∵Y=2X+1,
∴D(Y)=22D(X)=4D(X)=4×2.8=11.2.
12.两封信随机投入A,B,C三个空邮箱中,则A邮箱的信件数X的方差D(X)=________.
解析 X的所有可能取值为0,1,2,
13.某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分为n小块地,在总共2n小块地中,随机选n小块地种植品种甲,另外n小块地种植品种乙.假设n=4,在第一大块地中,种植品种甲的小块地的数目记为X,求X的分布列、均值及方差.
解 X可能的取值为0,1,2,3,4,
即X的分布列为
14.根据以往的经验,某工程施工期间的降水量X(单位:mm)对工期的影响如下表所示.
3
降水量X X<300 300≤X<700 700≤X<900 X≥900
工期延误天数Y 0 2 6 10
若历史气象资料表明,该工程施工期间降水量X小于300,700,900的概率分别为0.3,0.7,0.9,则工期延误天数Y的期望是________,工期延误天数Y的方差为________.
9.8
解析 由已知条件和概率的加法公式知,
P(X<300)=0.3,
P(300≤X<700)=P(X<700)-P(X<300)=0.7-0.3=0.4,
P(700≤X<900)=P(X<900)-P(X<700)=0.9-0.7=0.2,
P(X≥900)=1-P(X<900)=1-0.9=0.1.
所以随机变量Y的分布列为
Y 0 2 6 10
P 0.3 0.4 0.2 0.1
故E(Y)=0×0.3+2×0.4+6×0.2+10×0.1=3(天),
D(Y)=(0-3)2×0.3+(2-3)2×0.4+(6-3)2×0.2+(10-3)2×0.1=9.8.
故工期延误天数Y的方差为9.8.
本课结束
本课结束
