浙教版数学九年级上册 期中综合测试卷(含答案)
文档属性
| 名称 | 浙教版数学九年级上册 期中综合测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 671.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-14 16:30:23 | ||
图片预览


文档简介
期中综合测试卷
班级 学号 姓名 得分
一、选择题(本大题有10小题,每小题3分,共30分)
1. 抛物线 的顶点坐标是( )
A.(3,4) B. (-3,4) C. (3,—4) D. (2,4)
2.下列函数中,当x>0时,y随x的增大而增大的是( )
A. y=-x+1
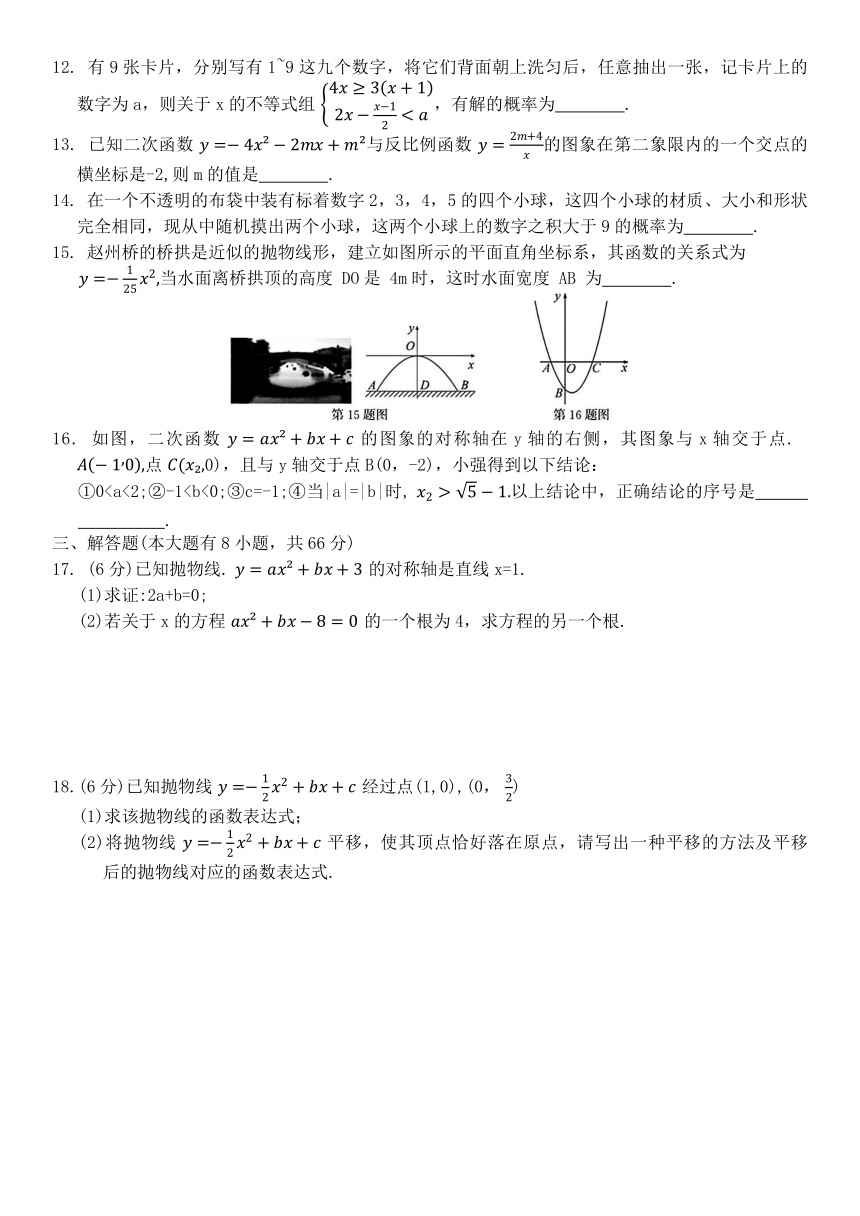
3.如图所示,在平行四边形纸片上做随机扎针试验,针头扎在阴影区域内的概率为( )
A B C D
4. 已知点(-3,y ),(-2,y ),(1,y )是抛物线. 上的点,则( )
5.如图,任意转动正六边形转盘一次,当转盘停止转动时,指针指向大于3的数的概率是( )
A B C D
6. 已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式 则下列说法中正确的是( )
A. 点火后9s和点火后 13s的升空高度相同 B. 点火后 24s火箭落于地面
C. 点火后 10s的升空高度为139m D. 火箭升空的最大高度为 145m
7.为了解某地区九年级男生的身高情况,随机抽取了该地区 100名九年级男生,他们的身高x( cm)统计如下表:
组别( cm) x<160 160≤x<170 170≤x<180 x≥180
人数 5 38 42 15
根据以上结果,抽查该地区一名九年级男生,估计他的身高不低于180cm的概率是( )
A. 0.85 B. 0.57 C. 0.42 D. 0.15
8. 已知二次函数 的图象如图所示,则该函数在所给自变量的取值范围内,下列说法正确的是( )
A. 有最小值0,有最大值3 B. 有最小值-1,有最大值0
C. 有最小值一1,有最大值3 D. 有最小值一1,无最大值
9. 对于题目“一段抛物线L:y=-x(x--3)+c(0≤x≤3)与直线l:y=x+2有唯一公共点,若c为整数,确定所有c的值.”甲的结果是c=1,乙的结果是c=3或4,则( )
A. 甲的结果正确 B. 乙的结果正确
C. 甲、乙的结果合在一起才正确 D. 甲、乙的结果合在一起也不正确
10.设函数. (a,h,k是实数,a≠0),当x=1时,y=1,当x=8时,y=8,则( )
A. 若h=4,则a<0 B. 若h=5,则a>0 C. 若h=6,则a<0 D. 若h=7,则a>0
二、填空题(本大题有6小题,每小题4分,共24分)
11. 把抛物线. 向上平移9个单位,那么所得抛物线与x轴的两个交点之间的距离是 .
12. 有9张卡片,分别写有1~9这九个数字,将它们背面朝上洗匀后,任意抽出一张,记卡片上的数字为a,则关于x的不等式组 ,有解的概率为 .
13. 已知二次函数 与反比例函数 的图象在第二象限内的一个交点的横坐标是-2,则m的值是 .
14. 在一个不透明的布袋中装有标着数字2,3,4,5的四个小球,这四个小球的材质、大小和形状完全相同,现从中随机摸出两个小球,这两个小球上的数字之积大于9的概率为 .
15. 赵州桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数的关系式为
当水面离桥拱顶的高度 DO是 4m时,这时水面宽度 AB 为 .
16. 如图,二次函数 的图象的对称轴在y轴的右侧,其图象与x轴交于点. 点 0),且与y轴交于点B(0,-2),小强得到以下结论:
①0三、解答题(本大题有8小题,共66分)
17. (6分)已知抛物线. 的对称轴是直线x=1.
(1)求证:2a+b=0;
(2)若关于x的方程 的一个根为4,求方程的另一个根.
18.(6分)已知抛物线 经过点(1,0),(0, )
(1)求该抛物线的函数表达式;
(2)将抛物线 平移,使其顶点恰好落在原点,请写出一种平移的方法及平移后的抛物线对应的函数表达式.
19.(6分)中国北京世界园艺博览会(以下简称“世园会”)于4月29日至10月7日在北京延庆区举行.世园会为满足大家的游览需求,倾情打造了4条各具特色的趣玩路线,分别是:“A解密世园会”、“B爱我家,爱园艺”、“C园艺小清新之旅”和“D快速车览之旅”.李欣和张帆都计划暑假去世园会,他们各自在这4条路线中任意选择一条路线游览,每条路线被选择的可能性相同.
(1) 李欣选择路线“C园艺小清新之旅”的概率是多少
(2)用画树状图或列表的方法,求李欣和张帆恰好选择同一路线游览的概率.
20.(8分)现有 A,B,C三个不透明的盒子,A盒中装有红球、黄球、蓝球各1个,B盒中装有红球、黄球各1个,C盒中装有红球、蓝球各1个,这些球除颜色外都相同.现分别从A,B,C三个盒子中任意摸出一个球.
(1)从A盒中摸出红球的概率为 ;
(2)用画树状图或列表的方法,求摸出的三个球中至少有一个红球的概率.
21.(8分)如图,在平面直角坐标系中,二次函数 的图象的顶点是A,与x轴交于B,C两点,与y轴交于点D,点 B的坐标是(1,0).
(1)求A,C两点的坐标,并根据图象直接写出当y>0时x的取值范围.
(2)平移该二次函数的图象,使点 D 恰好落在点A 的位置上,求平移后图象所对应的二次函数的表达式.
22.(10分)某校为了解学生课外阅读情况,就学生每周阅读时间随机调查了部分学生,调查结果按性别整理如下:女生阅读时间人数统计表
阅读时间t(小时) 人数 占女生人数百分比
0≤t<0.5 4 20%
0.5≤t<1 m 15%
1≤t<1.5 5 25%
1.5≤1<2 6 n
2≤t<2.5 2 10%
根据图表解答下列问题:
(1)在女生阅读时间人数统计表中,
(2)此次抽样调查中,共抽取了 名学生,学生阅读时间的中位数在 时间段;
(3)从阅读时间在2~2.5小时的5名学生中随机抽取2名学生参加市级阅读活动,恰好抽到男、女生各一名的概率是多少
23.(10分)已知抛物线
(1)当 时,求抛物线与x轴的交点坐标及对称轴;
(2)①试说明无论a为何值,抛物线 一定经过两个定点,并求出这两个定点的坐标;
②将抛物线 沿这两个定点所在直线翻折,得到抛物线C ,直接写出 C 的表达式;
(3)若(2)中抛物线 的顶点到x轴的距离为2,求a的值.
24.(12分)某体育用品商店试销一款成本为50元/个的排球,规定试销期间单价不低于成本价,且获利不得高于40%,经试销发现,销售量y(个)与销售单价x(元/个)之间满足如图所示的一次函数关系.
(1)试确定y与x之间的函数关系式(不用写x的取值范围);
(2)若该体育用品商店试销的这款排球所获得的利润为Q(元),试写出利润Q(元)与销售单价x(元/个)之间的函数关系式;当试销单价定为多少元/个时,该商店获得最大利润 最大利润是多少元
(3)若该商店试销这款排球所获得的利润不低于600元,请确定销售单价x的取值范围.
期中综合测试卷
1. A 2. B 3. B 4. B 5. D 6. D 7. D8. C 9. D 10. C
11. 6 112 13. -7 1 4 15. 20m
16. ①④ 解析:由图象可知抛物线开口向上,a>0.由函数图象经过点 A(-1,0),B(0,-2),对称轴在y轴的右侧可得 可得a-b=2,b<0,故a=2+b<2,综合可知00,b<0,故a=-b,又a-b=2,故可知a=1,b=-1,故原函数为. x--2,当y=0时,即 解之得 故正确答案为:①④.
17. (1)证明:∵抛物线 的对称轴是直线 去分母得2a=-b,移项得2a+b=0.(2)解:设方程的另一个根为m,则可知 由(1)知2a+b=0,即 +4=2,解得m=-2,即方程的另一个根为-2.
18. 解:(1)把((1,0),(0 代入抛物线的表达式得: 解得 则抛物线的表达式为 (2)抛物线的表达式为 将抛物线向右平移1个单位,向下平移2个单位,此时顶点恰好落在原点,表达式变为
19. 解:(1)在这四条路线中任选一条,每条被选中的可能性相同,∴在四条路线中,李欣选择路线“C园艺小清新之旅”的概率是 (2)画树状图如图,共有16种等可能的结果,李欣和张帆恰好选择同一路线游览的结果有4种,∴李欣和张帆恰好选择同一路线游览的概率为
20. (1) (2)解:画树状图如图所示,共有 12种等可能的结果,摸出的三个球中至少有一个红球的结果有10种,∴摸出的三个球中至少有一个红球的概率为
21. 解:(1)把B(1,0)代入 得0=a+4-3,解得 ∴点A的坐标为(2,1).∵抛物线的对称轴为直线x=2,且点C与点 B关于对称轴对称,∴点C(3,0),∴当y>0时,x的取值范围是1(2)∵D(0,-3),∴点 D移到点A时,抛物线向右平移2个单位,向上平移4个单位,平移后图象所对应的二次函数的表达式为
22. 解:(1)3 30% (2)50 1≤t<1.5 (3)阅读时间在2~2.5小时的有女生2名,男生3名.
画树状图如图,共有 20种等可能情况,则恰好抽到男、女生各一名的概率是
23. 解:(1)抛物线与x轴的交点坐标为(5,0),(-1,0),对称轴为直线 x=2. ( ax-4a)-5,当x=0时,y=-5,抛物线. 4ax-5恒经过点(0,-5);当x=4时,y=-5,抛物线 恒经过点(4,-5).②C 的表达式: (3)依题意得: 或4a-- 或
24. 解:(1)设一次函数的表达式为y= kx+b,将(55,65),(60,60)代入得 解得 所以y与x之间的函数关系式为y=-x+120. ∵成本为50元/个的排球,规定试销期间单价不低于成本价,且获利不得高于40%,∴50≤x≤70,∴当试销单价定为70元/个时,该商店可获得最大利润,最大利润为 1000 元.
(3)依题意得 单价x的取值范围为
班级 学号 姓名 得分
一、选择题(本大题有10小题,每小题3分,共30分)
1. 抛物线 的顶点坐标是( )
A.(3,4) B. (-3,4) C. (3,—4) D. (2,4)
2.下列函数中,当x>0时,y随x的增大而增大的是( )
A. y=-x+1
3.如图所示,在平行四边形纸片上做随机扎针试验,针头扎在阴影区域内的概率为( )
A B C D
4. 已知点(-3,y ),(-2,y ),(1,y )是抛物线. 上的点,则( )
5.如图,任意转动正六边形转盘一次,当转盘停止转动时,指针指向大于3的数的概率是( )
A B C D
6. 已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式 则下列说法中正确的是( )
A. 点火后9s和点火后 13s的升空高度相同 B. 点火后 24s火箭落于地面
C. 点火后 10s的升空高度为139m D. 火箭升空的最大高度为 145m
7.为了解某地区九年级男生的身高情况,随机抽取了该地区 100名九年级男生,他们的身高x( cm)统计如下表:
组别( cm) x<160 160≤x<170 170≤x<180 x≥180
人数 5 38 42 15
根据以上结果,抽查该地区一名九年级男生,估计他的身高不低于180cm的概率是( )
A. 0.85 B. 0.57 C. 0.42 D. 0.15
8. 已知二次函数 的图象如图所示,则该函数在所给自变量的取值范围内,下列说法正确的是( )
A. 有最小值0,有最大值3 B. 有最小值-1,有最大值0
C. 有最小值一1,有最大值3 D. 有最小值一1,无最大值
9. 对于题目“一段抛物线L:y=-x(x--3)+c(0≤x≤3)与直线l:y=x+2有唯一公共点,若c为整数,确定所有c的值.”甲的结果是c=1,乙的结果是c=3或4,则( )
A. 甲的结果正确 B. 乙的结果正确
C. 甲、乙的结果合在一起才正确 D. 甲、乙的结果合在一起也不正确
10.设函数. (a,h,k是实数,a≠0),当x=1时,y=1,当x=8时,y=8,则( )
A. 若h=4,则a<0 B. 若h=5,则a>0 C. 若h=6,则a<0 D. 若h=7,则a>0
二、填空题(本大题有6小题,每小题4分,共24分)
11. 把抛物线. 向上平移9个单位,那么所得抛物线与x轴的两个交点之间的距离是 .
12. 有9张卡片,分别写有1~9这九个数字,将它们背面朝上洗匀后,任意抽出一张,记卡片上的数字为a,则关于x的不等式组 ,有解的概率为 .
13. 已知二次函数 与反比例函数 的图象在第二象限内的一个交点的横坐标是-2,则m的值是 .
14. 在一个不透明的布袋中装有标着数字2,3,4,5的四个小球,这四个小球的材质、大小和形状完全相同,现从中随机摸出两个小球,这两个小球上的数字之积大于9的概率为 .
15. 赵州桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数的关系式为
当水面离桥拱顶的高度 DO是 4m时,这时水面宽度 AB 为 .
16. 如图,二次函数 的图象的对称轴在y轴的右侧,其图象与x轴交于点. 点 0),且与y轴交于点B(0,-2),小强得到以下结论:
①0
17. (6分)已知抛物线. 的对称轴是直线x=1.
(1)求证:2a+b=0;
(2)若关于x的方程 的一个根为4,求方程的另一个根.
18.(6分)已知抛物线 经过点(1,0),(0, )
(1)求该抛物线的函数表达式;
(2)将抛物线 平移,使其顶点恰好落在原点,请写出一种平移的方法及平移后的抛物线对应的函数表达式.
19.(6分)中国北京世界园艺博览会(以下简称“世园会”)于4月29日至10月7日在北京延庆区举行.世园会为满足大家的游览需求,倾情打造了4条各具特色的趣玩路线,分别是:“A解密世园会”、“B爱我家,爱园艺”、“C园艺小清新之旅”和“D快速车览之旅”.李欣和张帆都计划暑假去世园会,他们各自在这4条路线中任意选择一条路线游览,每条路线被选择的可能性相同.
(1) 李欣选择路线“C园艺小清新之旅”的概率是多少
(2)用画树状图或列表的方法,求李欣和张帆恰好选择同一路线游览的概率.
20.(8分)现有 A,B,C三个不透明的盒子,A盒中装有红球、黄球、蓝球各1个,B盒中装有红球、黄球各1个,C盒中装有红球、蓝球各1个,这些球除颜色外都相同.现分别从A,B,C三个盒子中任意摸出一个球.
(1)从A盒中摸出红球的概率为 ;
(2)用画树状图或列表的方法,求摸出的三个球中至少有一个红球的概率.
21.(8分)如图,在平面直角坐标系中,二次函数 的图象的顶点是A,与x轴交于B,C两点,与y轴交于点D,点 B的坐标是(1,0).
(1)求A,C两点的坐标,并根据图象直接写出当y>0时x的取值范围.
(2)平移该二次函数的图象,使点 D 恰好落在点A 的位置上,求平移后图象所对应的二次函数的表达式.
22.(10分)某校为了解学生课外阅读情况,就学生每周阅读时间随机调查了部分学生,调查结果按性别整理如下:女生阅读时间人数统计表
阅读时间t(小时) 人数 占女生人数百分比
0≤t<0.5 4 20%
0.5≤t<1 m 15%
1≤t<1.5 5 25%
1.5≤1<2 6 n
2≤t<2.5 2 10%
根据图表解答下列问题:
(1)在女生阅读时间人数统计表中,
(2)此次抽样调查中,共抽取了 名学生,学生阅读时间的中位数在 时间段;
(3)从阅读时间在2~2.5小时的5名学生中随机抽取2名学生参加市级阅读活动,恰好抽到男、女生各一名的概率是多少
23.(10分)已知抛物线
(1)当 时,求抛物线与x轴的交点坐标及对称轴;
(2)①试说明无论a为何值,抛物线 一定经过两个定点,并求出这两个定点的坐标;
②将抛物线 沿这两个定点所在直线翻折,得到抛物线C ,直接写出 C 的表达式;
(3)若(2)中抛物线 的顶点到x轴的距离为2,求a的值.
24.(12分)某体育用品商店试销一款成本为50元/个的排球,规定试销期间单价不低于成本价,且获利不得高于40%,经试销发现,销售量y(个)与销售单价x(元/个)之间满足如图所示的一次函数关系.
(1)试确定y与x之间的函数关系式(不用写x的取值范围);
(2)若该体育用品商店试销的这款排球所获得的利润为Q(元),试写出利润Q(元)与销售单价x(元/个)之间的函数关系式;当试销单价定为多少元/个时,该商店获得最大利润 最大利润是多少元
(3)若该商店试销这款排球所获得的利润不低于600元,请确定销售单价x的取值范围.
期中综合测试卷
1. A 2. B 3. B 4. B 5. D 6. D 7. D8. C 9. D 10. C
11. 6 112 13. -7 1 4 15. 20m
16. ①④ 解析:由图象可知抛物线开口向上,a>0.由函数图象经过点 A(-1,0),B(0,-2),对称轴在y轴的右侧可得 可得a-b=2,b<0,故a=2+b<2,综合可知0
17. (1)证明:∵抛物线 的对称轴是直线 去分母得2a=-b,移项得2a+b=0.(2)解:设方程的另一个根为m,则可知 由(1)知2a+b=0,即 +4=2,解得m=-2,即方程的另一个根为-2.
18. 解:(1)把((1,0),(0 代入抛物线的表达式得: 解得 则抛物线的表达式为 (2)抛物线的表达式为 将抛物线向右平移1个单位,向下平移2个单位,此时顶点恰好落在原点,表达式变为
19. 解:(1)在这四条路线中任选一条,每条被选中的可能性相同,∴在四条路线中,李欣选择路线“C园艺小清新之旅”的概率是 (2)画树状图如图,共有16种等可能的结果,李欣和张帆恰好选择同一路线游览的结果有4种,∴李欣和张帆恰好选择同一路线游览的概率为
20. (1) (2)解:画树状图如图所示,共有 12种等可能的结果,摸出的三个球中至少有一个红球的结果有10种,∴摸出的三个球中至少有一个红球的概率为
21. 解:(1)把B(1,0)代入 得0=a+4-3,解得 ∴点A的坐标为(2,1).∵抛物线的对称轴为直线x=2,且点C与点 B关于对称轴对称,∴点C(3,0),∴当y>0时,x的取值范围是1
22. 解:(1)3 30% (2)50 1≤t<1.5 (3)阅读时间在2~2.5小时的有女生2名,男生3名.
画树状图如图,共有 20种等可能情况,则恰好抽到男、女生各一名的概率是
23. 解:(1)抛物线与x轴的交点坐标为(5,0),(-1,0),对称轴为直线 x=2. ( ax-4a)-5,当x=0时,y=-5,抛物线. 4ax-5恒经过点(0,-5);当x=4时,y=-5,抛物线 恒经过点(4,-5).②C 的表达式: (3)依题意得: 或4a-- 或
24. 解:(1)设一次函数的表达式为y= kx+b,将(55,65),(60,60)代入得 解得 所以y与x之间的函数关系式为y=-x+120. ∵成本为50元/个的排球,规定试销期间单价不低于成本价,且获利不得高于40%,∴50≤x≤70,∴当试销单价定为70元/个时,该商店可获得最大利润,最大利润为 1000 元.
(3)依题意得 单价x的取值范围为
同课章节目录
