3.1搭积木比赛基础练习(含答案) 北师大版数学六年级上册
文档属性
| 名称 | 3.1搭积木比赛基础练习(含答案) 北师大版数学六年级上册 |
|
|
| 格式 | doc | ||
| 文件大小 | 637.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-14 00:00:00 | ||
图片预览



文档简介
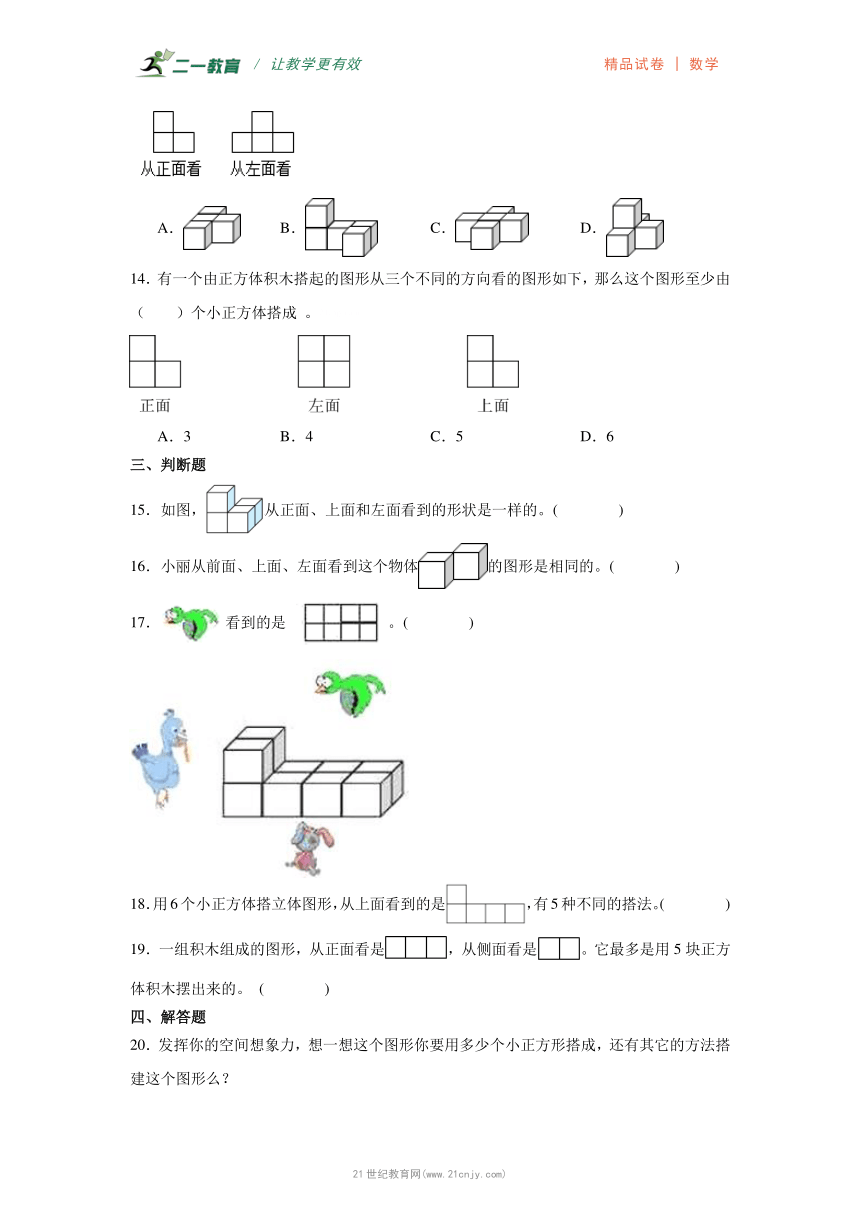
/ 让教学更有效 精品试卷 | 数学
3.1搭积木比赛
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.给下图再增加1个同样的小正方体,添加的小正方体与其他小正方体至少有一个面重合。要使从正面看到的图形不变,有( )种不同的摆法。21*cnjy*com
2.小明搭了一个立体图形,请你分别指出下面的形状是他从上面、正面还是右面看到的.
是从( )面看到的;
是从( )面看到的.
3.一个立体图形,从上面看到的形状是,从正面看到的形状是。搭这样的立体图形,最少需要( )小立方块,最多需要( )小立方块。
4.一个立体图形从左面看是,从上面看是,要搭成这样的立体图形,至少要用( )个小正方体。21·世纪*教育网
5.一个立体图形从上面看到的形状是,从左面看到的形状是。要搭成这样的立体图形,至少要用( )个小正方体,最多要用( )个小正方体。
6.
有这样一个由( )块相同的小正方体木块摆成的立体图形(如图).如果我们用红色的油漆把它的表面涂上颜色.那么,有( )个小正方体只有1面是红色的;有( )个小正方体只有2面是红色的;有3面是红色的小正方体个数是( );( )个小正方体有4面带有红色;5个面是红色的小正方体有( )个;( )个小正方体每个面都被涂上了红色.【来源:21·世纪·教育·网】
7.用小正方体搭成的一个立体图形(面和面粘连),从正面看是,从左面看是,搭这个立体图形最少用了( )个小正方体,最多用了( )个小正方体。
二、选择题
8.一个立体图形,从上面和正面看到的形状都是,要搭成这个立体图形,至少需要( )个小正方体。2-1-c-n-j-y
A.7 B.6 C.5 D.10
9.一个立体图形从正面看到的形状是,从左面看到的形状是,搭这样的立体图形,至少需要( )个小正方体。21教育名师原创作品
A.4 B.5 C.6 D.7
10.下面立体图形中,从正面、左面和右面看形状完全相同的是( )。
A. B. C. D.
11.下面两个图形,从( )面看到的形状是不同的。
A.上面 B.前面 C.侧面 D.后面
12.观察下面的立体图形,从右面看到的形状是( )。
A. B. C. D.
13.由几个相同的小正方体搭成的几何体,从两个不同的方向看到的形状如下图所示,则搭成的立体图形可能是( )。
A. B. C. D.
14.有一个由正方体积木搭起的图形从三个不同的方向看的图形如下,那么这个图形至少由( )个小正方体搭成 。21cnjy.com
A.3 B.4 C.5 D.6
三、判断题
15.如图,从正面、上面和左面看到的形状是一样的。( )
16.小丽从前面、上面、左面看到这个物体的图形是相同的。( )
17.看到的是 。( )
18.用6个小正方体搭立体图形,从上面看到的是,有5种不同的搭法。( )
19.一组积木组成的图形,从正面看是,从侧面看是。它最多是用5块正方体积木摆出来的。 ( )
四、解答题
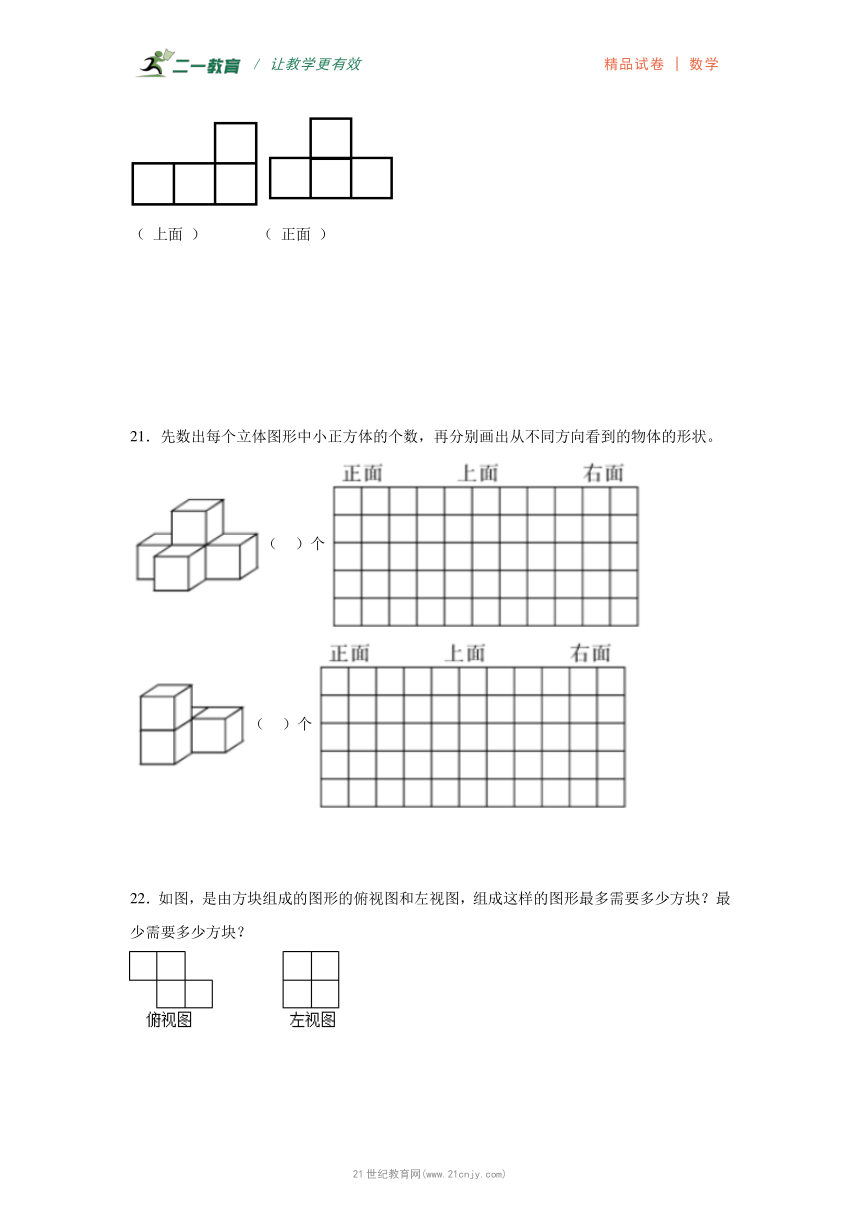
20.发挥你的空间想象力,想一想这个图形你要用多少个小正方形搭成,还有其它的方法搭建这个图形么?
( 上面 ) ( 正面 )
21.先数出每个立体图形中小正方体的个数,再分别画出从不同方向看到的物体的形状。
( )个
( )个
22.如图,是由方块组成的图形的俯视图和左视图,组成这样的图形最多需要多少方块?最少需要多少方块?
23.在下图中添上一个同样大小的正方体,使其从左面,上面两个不同的位置观察时,所看到的图形都不变,应该怎样摆?【版权所有:21教育】
24.按要求摆小正方体:用5个小正方体摆从正面看到的图形(你能摆出几种不同的方法)。
参考答案:
1.6
【分析】根据题意,要使从正面看到的图形不变,则增加的小正方体可以挡住原图形底层任意一个小正方体,也可以被底层任意一个小正方体挡住,即可以放在原图形底层任意一个小正方体的前面或后面。底层有3个小正方体,3+3=6(种)。21世纪教育网版权所有
【详解】通过分析,要使从正面看到的图形不变,增加的小正方体可以放在原图形底层任意一个小正方体的前面或后面,有6种不同的摆法。
【点睛】本题考查立体图形三视图的认识。需要认真观察,运用空间想象力解答此类问题。
2. 右 正
【分析】观察图形可知,从正面看到的图形是2层:下层3个正方形,上层1个靠左边;从右面看到的图形是2层:下层2个正方形,上层1个靠右边;从上面看到的图形是两行:后面一行3个正方形,前面一行靠左边,据此即可解答问题.
【详解】根据分析可得:
是从右面看到的;
是从正面看到的.
故答案为右,正.
3. 5 6
【分析】这个立方体图形,从正面看是3个正方形,说明此图形分两层,下层至少2个小正方块,上层至少1个小正方块居左;从上面看是4个正方形,可以确定此图形下层有4个小正方块,上层左边有1个或2个小正方体,据此解答即可。
【详解】
根据分析可知,如图:
最少:4+1=5(个)
最多:4+2=6(个)
一个立体图形,从上面看到的形状是,从正面看到的形状是。搭这样的立体图形,最少需要5个立方块,最多需要6个立方块。
4.5
【分析】
根据观察物体的方法,从上面看是,可知底层有4个小正方体,左面看是,可知有2层,上层至少有1个小正方体,据此解答即可。
【详解】
分析可知,从上面看是,可知底层有4个小正方体,左面看是,可知有2层,上层至少有1个小正方体,所以要搭成这样的立体图形,至少要用(个)小正方体。至少要用(5)个小正方体。2·1·c·n·j·y
【点评】本题考查了从不同方向观察物体确定几何体的样子,培养了学生的观察能力。
5. 6 8
【分析】根据观察物体的方法,从上面看到的形状是:,可知底层有4个小正方体,从左面看到的形状是:,可知这个立体图形有前后两排,有3层;据此画出符合条件的立体图形即可解题。
【详解】由分析可知,符合条件的立体图形可以是:
(6个)、(7个)、(8个),
所以,一个立体图形从上面看到的形状是,从左面看到的形状是。要搭成这样的立体图形,至少要用6个小正方体,最多要用8个小正方体。
6. 8 1 0 1 4 2 0
【解析】略
7. 5 7
【解析】略
8.A
【分析】观察题意可知几何体有两层,根据从上面和正面看到的形状可知,下层有5个小正方体,上层最少有2个,然后根据加法计算出这个立体图形最少有几个小正方体。
【详解】5+2=7(个)
要搭成这个立体图形,至少需要7个小正方体。
故答案为:A
【点睛】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
9.B
【分析】从正面看下层有3个小正方体,上层1个小正方体;从左面看,下层有2个小正方体,上层1个小正方体,由此可知,下层最少有4个小正方体,上层最少有1个小正方体,至少有(4+1)个小正方体,据此解答。【来源:21cnj*y.co*m】
【详解】4+1=5(个)
一个立体图形从正面看到的形状是,从左面看到的形状是,搭这样的立体图形,至少需要5个小正方体。
故答案为:B
【点睛】本题考查从不同方向观察物体和几何体,关键是培养观察能力。
10.D
【分析】观察图形,分别找出四个选项中的图形从正面和左面和右面看到的图形,再比较即可解答问题。
【详解】A.,从正面看;从左面看;从右面看,看到的形状不完全一样;
B.,从正面看,从左面看,从右面看,看到的形状不相同;
C.,从正面看,从左面看,从右面看,看到的形状不相同;
D.,从正面看,从左面看,从右面看,看到的形状完全相同。
故答案为:D
【点睛】本题考查对三视图的理解应用及空间想象能力。
11.A
【分析】物体的三视图特指主视图、俯视图和左视图。
主视图:在正面内得到的由前向后观察物体的视图,叫做主视图;
俯视图:在水平面内得到的由上向下观察物体的视图,叫做俯视图;
左视图:在侧面内得到的由左向右观察物体的视图,叫做左视图,有时也叫做侧视图;
【详解】A.从上面看到的形状,左图能看到4个正方形,分两层,上层3个,下层1个,右对齐;右图能看到4个正方形,分两层,上层1个,下层3个,右对齐,所以从上面看到的形状不相同;【出处:21教育名师】
B.从前面看都能看到一行3个正方形,所以从前面看到的形状相同;
C.从侧面看都能看到一行2个正方形,所以从侧面看到的形状相同;
D.从后面看都能看到一行3个正方形,所以从后面看到的形状相同。
故答案为:A
【点睛】此题考查的是从不同方向观察几何图形,培养学生的观察能力。
12.B
【分析】从右边看到的2层,下层有2个正方形,上层有1个正方形,右齐,据此解答。
【详解】根据分析可知,从右面看到的图形是。
故答案选:B
【点睛】本题考查了从不同方向观察物体和几何体,锻炼空间想象力和抽象思维能力。
13.D
【分析】分别判断选项中的立体图形从左面观察到的平面图和从正面观察到的平面图,并与题中的平面图相比较即可。21·cn·jy·com
【详解】A.不合题意,错误;
B.不合题意,错误;
C.不合题意,错误;
D.符合题意,正确。
故答案为:D
【点睛】本题时也可以根据题目中的平面图形还原立体图形用排除法解答。
14.C
【解析】略
15.×
【分析】分别画出这这个图形从正面、上面和左面看到的图形,再判断即可。
【详解】
从正面看是,从上面看是,从左面看是,所以从正面、上面和左面看到的形状是不一样的,原题说法错误。21教育网
故答案为:×
16.×
【分析】根据从前面、左面和上面看到的形状判断即可。
【详解】从前面和左面看到的形状是,从上面看到的形状是。所以从前面、上面、左面看到这个物体的图形是不相同的。原题说法错误。
故答案为:×
【点睛】本题主要考查从不同发现观察物体和几何体,关键培养学生的观察能力。
17.√
【分析】从不同的方向观察到的形状是不同的,判断出从前面看到的有几个正方形以及每个小正方形的位置即可做出选择。www.21-cn-jy.com
【详解】从图中可以看到,小鸟是在几何体的上方,所以它看到的形状是 。
故答案为:√
【点睛】此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力。
18.√
【分析】用6个小正方体搭立体图形,从上面看到的是,则这个立体图形的底层由5个小正方体组成,且摆放形状为,第6个小正方体可以摆放在底层的任意一个小正方体的上面,所以有5种不同的搭法。www-2-1-cnjy-com
【详解】由分析可知:
用6个小正方体搭立体图形,从上面看到的是,有5种不同的搭法。原题干说法正确。
故答案为:√
【点睛】本题考查根据三视图确认立体图形,运用空间想象力是解题的关键。
19.×
【详解】略
20.5个可以搭建(答案不唯一)
【详解】略
21.5;正面 上面 右面
4;正面 上面 右面
【解析】略
22.6块;8块
【分析】根据从上面、左面看到的形状,所用的小正方体分前、后两排,上、下两层。下层前、后排各两个,前排左边一个与后排右面一个对齐;上层前、后排最少各放1个,最多各放2个。21*cnjy*com
【详解】如图
组成这样的图形最少需要6个方块,最多需要8个方块(下图):
23.在③的上面再摆一个小正方体,就能使从左面和上面看到的图形都不变
【详解】略
【点睛】
24.(1)可以在左边的正方体后面连续摆3个。(答案不唯一)
(2)在左边最下边正方体后面连续摆2个。(答案不唯一)
(3)在正面图形的后面任意位置都可以摆放1个正方体。(答案不唯一)
【详解】略
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
3.1搭积木比赛
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.给下图再增加1个同样的小正方体,添加的小正方体与其他小正方体至少有一个面重合。要使从正面看到的图形不变,有( )种不同的摆法。21*cnjy*com
2.小明搭了一个立体图形,请你分别指出下面的形状是他从上面、正面还是右面看到的.
是从( )面看到的;
是从( )面看到的.
3.一个立体图形,从上面看到的形状是,从正面看到的形状是。搭这样的立体图形,最少需要( )小立方块,最多需要( )小立方块。
4.一个立体图形从左面看是,从上面看是,要搭成这样的立体图形,至少要用( )个小正方体。21·世纪*教育网
5.一个立体图形从上面看到的形状是,从左面看到的形状是。要搭成这样的立体图形,至少要用( )个小正方体,最多要用( )个小正方体。
6.
有这样一个由( )块相同的小正方体木块摆成的立体图形(如图).如果我们用红色的油漆把它的表面涂上颜色.那么,有( )个小正方体只有1面是红色的;有( )个小正方体只有2面是红色的;有3面是红色的小正方体个数是( );( )个小正方体有4面带有红色;5个面是红色的小正方体有( )个;( )个小正方体每个面都被涂上了红色.【来源:21·世纪·教育·网】
7.用小正方体搭成的一个立体图形(面和面粘连),从正面看是,从左面看是,搭这个立体图形最少用了( )个小正方体,最多用了( )个小正方体。
二、选择题
8.一个立体图形,从上面和正面看到的形状都是,要搭成这个立体图形,至少需要( )个小正方体。2-1-c-n-j-y
A.7 B.6 C.5 D.10
9.一个立体图形从正面看到的形状是,从左面看到的形状是,搭这样的立体图形,至少需要( )个小正方体。21教育名师原创作品
A.4 B.5 C.6 D.7
10.下面立体图形中,从正面、左面和右面看形状完全相同的是( )。
A. B. C. D.
11.下面两个图形,从( )面看到的形状是不同的。
A.上面 B.前面 C.侧面 D.后面
12.观察下面的立体图形,从右面看到的形状是( )。
A. B. C. D.
13.由几个相同的小正方体搭成的几何体,从两个不同的方向看到的形状如下图所示,则搭成的立体图形可能是( )。
A. B. C. D.
14.有一个由正方体积木搭起的图形从三个不同的方向看的图形如下,那么这个图形至少由( )个小正方体搭成 。21cnjy.com
A.3 B.4 C.5 D.6
三、判断题
15.如图,从正面、上面和左面看到的形状是一样的。( )
16.小丽从前面、上面、左面看到这个物体的图形是相同的。( )
17.看到的是 。( )
18.用6个小正方体搭立体图形,从上面看到的是,有5种不同的搭法。( )
19.一组积木组成的图形,从正面看是,从侧面看是。它最多是用5块正方体积木摆出来的。 ( )
四、解答题
20.发挥你的空间想象力,想一想这个图形你要用多少个小正方形搭成,还有其它的方法搭建这个图形么?
( 上面 ) ( 正面 )
21.先数出每个立体图形中小正方体的个数,再分别画出从不同方向看到的物体的形状。
( )个
( )个
22.如图,是由方块组成的图形的俯视图和左视图,组成这样的图形最多需要多少方块?最少需要多少方块?
23.在下图中添上一个同样大小的正方体,使其从左面,上面两个不同的位置观察时,所看到的图形都不变,应该怎样摆?【版权所有:21教育】
24.按要求摆小正方体:用5个小正方体摆从正面看到的图形(你能摆出几种不同的方法)。
参考答案:
1.6
【分析】根据题意,要使从正面看到的图形不变,则增加的小正方体可以挡住原图形底层任意一个小正方体,也可以被底层任意一个小正方体挡住,即可以放在原图形底层任意一个小正方体的前面或后面。底层有3个小正方体,3+3=6(种)。21世纪教育网版权所有
【详解】通过分析,要使从正面看到的图形不变,增加的小正方体可以放在原图形底层任意一个小正方体的前面或后面,有6种不同的摆法。
【点睛】本题考查立体图形三视图的认识。需要认真观察,运用空间想象力解答此类问题。
2. 右 正
【分析】观察图形可知,从正面看到的图形是2层:下层3个正方形,上层1个靠左边;从右面看到的图形是2层:下层2个正方形,上层1个靠右边;从上面看到的图形是两行:后面一行3个正方形,前面一行靠左边,据此即可解答问题.
【详解】根据分析可得:
是从右面看到的;
是从正面看到的.
故答案为右,正.
3. 5 6
【分析】这个立方体图形,从正面看是3个正方形,说明此图形分两层,下层至少2个小正方块,上层至少1个小正方块居左;从上面看是4个正方形,可以确定此图形下层有4个小正方块,上层左边有1个或2个小正方体,据此解答即可。
【详解】
根据分析可知,如图:
最少:4+1=5(个)
最多:4+2=6(个)
一个立体图形,从上面看到的形状是,从正面看到的形状是。搭这样的立体图形,最少需要5个立方块,最多需要6个立方块。
4.5
【分析】
根据观察物体的方法,从上面看是,可知底层有4个小正方体,左面看是,可知有2层,上层至少有1个小正方体,据此解答即可。
【详解】
分析可知,从上面看是,可知底层有4个小正方体,左面看是,可知有2层,上层至少有1个小正方体,所以要搭成这样的立体图形,至少要用(个)小正方体。至少要用(5)个小正方体。2·1·c·n·j·y
【点评】本题考查了从不同方向观察物体确定几何体的样子,培养了学生的观察能力。
5. 6 8
【分析】根据观察物体的方法,从上面看到的形状是:,可知底层有4个小正方体,从左面看到的形状是:,可知这个立体图形有前后两排,有3层;据此画出符合条件的立体图形即可解题。
【详解】由分析可知,符合条件的立体图形可以是:
(6个)、(7个)、(8个),
所以,一个立体图形从上面看到的形状是,从左面看到的形状是。要搭成这样的立体图形,至少要用6个小正方体,最多要用8个小正方体。
6. 8 1 0 1 4 2 0
【解析】略
7. 5 7
【解析】略
8.A
【分析】观察题意可知几何体有两层,根据从上面和正面看到的形状可知,下层有5个小正方体,上层最少有2个,然后根据加法计算出这个立体图形最少有几个小正方体。
【详解】5+2=7(个)
要搭成这个立体图形,至少需要7个小正方体。
故答案为:A
【点睛】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
9.B
【分析】从正面看下层有3个小正方体,上层1个小正方体;从左面看,下层有2个小正方体,上层1个小正方体,由此可知,下层最少有4个小正方体,上层最少有1个小正方体,至少有(4+1)个小正方体,据此解答。【来源:21cnj*y.co*m】
【详解】4+1=5(个)
一个立体图形从正面看到的形状是,从左面看到的形状是,搭这样的立体图形,至少需要5个小正方体。
故答案为:B
【点睛】本题考查从不同方向观察物体和几何体,关键是培养观察能力。
10.D
【分析】观察图形,分别找出四个选项中的图形从正面和左面和右面看到的图形,再比较即可解答问题。
【详解】A.,从正面看;从左面看;从右面看,看到的形状不完全一样;
B.,从正面看,从左面看,从右面看,看到的形状不相同;
C.,从正面看,从左面看,从右面看,看到的形状不相同;
D.,从正面看,从左面看,从右面看,看到的形状完全相同。
故答案为:D
【点睛】本题考查对三视图的理解应用及空间想象能力。
11.A
【分析】物体的三视图特指主视图、俯视图和左视图。
主视图:在正面内得到的由前向后观察物体的视图,叫做主视图;
俯视图:在水平面内得到的由上向下观察物体的视图,叫做俯视图;
左视图:在侧面内得到的由左向右观察物体的视图,叫做左视图,有时也叫做侧视图;
【详解】A.从上面看到的形状,左图能看到4个正方形,分两层,上层3个,下层1个,右对齐;右图能看到4个正方形,分两层,上层1个,下层3个,右对齐,所以从上面看到的形状不相同;【出处:21教育名师】
B.从前面看都能看到一行3个正方形,所以从前面看到的形状相同;
C.从侧面看都能看到一行2个正方形,所以从侧面看到的形状相同;
D.从后面看都能看到一行3个正方形,所以从后面看到的形状相同。
故答案为:A
【点睛】此题考查的是从不同方向观察几何图形,培养学生的观察能力。
12.B
【分析】从右边看到的2层,下层有2个正方形,上层有1个正方形,右齐,据此解答。
【详解】根据分析可知,从右面看到的图形是。
故答案选:B
【点睛】本题考查了从不同方向观察物体和几何体,锻炼空间想象力和抽象思维能力。
13.D
【分析】分别判断选项中的立体图形从左面观察到的平面图和从正面观察到的平面图,并与题中的平面图相比较即可。21·cn·jy·com
【详解】A.不合题意,错误;
B.不合题意,错误;
C.不合题意,错误;
D.符合题意,正确。
故答案为:D
【点睛】本题时也可以根据题目中的平面图形还原立体图形用排除法解答。
14.C
【解析】略
15.×
【分析】分别画出这这个图形从正面、上面和左面看到的图形,再判断即可。
【详解】
从正面看是,从上面看是,从左面看是,所以从正面、上面和左面看到的形状是不一样的,原题说法错误。21教育网
故答案为:×
16.×
【分析】根据从前面、左面和上面看到的形状判断即可。
【详解】从前面和左面看到的形状是,从上面看到的形状是。所以从前面、上面、左面看到这个物体的图形是不相同的。原题说法错误。
故答案为:×
【点睛】本题主要考查从不同发现观察物体和几何体,关键培养学生的观察能力。
17.√
【分析】从不同的方向观察到的形状是不同的,判断出从前面看到的有几个正方形以及每个小正方形的位置即可做出选择。www.21-cn-jy.com
【详解】从图中可以看到,小鸟是在几何体的上方,所以它看到的形状是 。
故答案为:√
【点睛】此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力。
18.√
【分析】用6个小正方体搭立体图形,从上面看到的是,则这个立体图形的底层由5个小正方体组成,且摆放形状为,第6个小正方体可以摆放在底层的任意一个小正方体的上面,所以有5种不同的搭法。www-2-1-cnjy-com
【详解】由分析可知:
用6个小正方体搭立体图形,从上面看到的是,有5种不同的搭法。原题干说法正确。
故答案为:√
【点睛】本题考查根据三视图确认立体图形,运用空间想象力是解题的关键。
19.×
【详解】略
20.5个可以搭建(答案不唯一)
【详解】略
21.5;正面 上面 右面
4;正面 上面 右面
【解析】略
22.6块;8块
【分析】根据从上面、左面看到的形状,所用的小正方体分前、后两排,上、下两层。下层前、后排各两个,前排左边一个与后排右面一个对齐;上层前、后排最少各放1个,最多各放2个。21*cnjy*com
【详解】如图
组成这样的图形最少需要6个方块,最多需要8个方块(下图):
23.在③的上面再摆一个小正方体,就能使从左面和上面看到的图形都不变
【详解】略
【点睛】
24.(1)可以在左边的正方体后面连续摆3个。(答案不唯一)
(2)在左边最下边正方体后面连续摆2个。(答案不唯一)
(3)在正面图形的后面任意位置都可以摆放1个正方体。(答案不唯一)
【详解】略
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
