八年级数学北师大版(2012)上册 5.3应用二元一次方程组—鸡兔同笼——课时优化训练(含详解)
文档属性
| 名称 | 八年级数学北师大版(2012)上册 5.3应用二元一次方程组—鸡兔同笼——课时优化训练(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 275.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-14 12:17:58 | ||
图片预览



文档简介
5.3应用二元一次方程组—鸡兔同笼——八年级数学北师大版(2012)上册课时优化训练
1.《孙子算经》中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,长木还剩余l尺,问木长多少尺?若设木长尺,绳子长尺,则可列方程组为( )
A. B. C. D.
2.小华和爸爸玩“掷飞镖”游戏.游戏规则:小华投中1次得5分,爸爸投中1次得3分,两人一共投中30次.经过计算发现爸爸比小华多得2分.设小华投中的次数为x,爸爸投中的次数为y,根据题意列出的方程组正确的是( )
A. B. C. D.
3.若干名学生一起去种树,如果每人种4棵,则还剩下3棵树苗;如果每人种5棵,则缺少5棵树苗,设学生有x人,树苗有y棵,根据题意可列出方程组( )
A. B. C. D.
4.如图,宽为的矩形图案是由10个形状和大小完全一样的小长方形拼成,则一个小长方形的面积为( )
A. B. C. D.
5.《九章算术》中有一题:“今有大器五、小器一容三斛;大器一、小器五容二斛.问大、小器各容几何?”译文:今有大容器5个,小容器1个,总容量为3斛(斛:古代容是单位);大容器1个,小容器5个,总容暴为2斛.问大容器、小容器的容量各是多少斛?设大容器的容量为x斛,小容器的容量为y斛,则可列方程组是( )
A. B. C. D.
6.数学家朱世杰所著的《四元玉鉴》是中国元代重要的数学著作之一,书中记载着这样一个问题,大意是:999文钱买了周果和苦果共1000个,11文钱可买9个甜果,4文钱可买7个苦果,问甜果,苦果各买了多少个?设买了甜果x个,苦果y个,则可列方程组为( )
A. B. C. D.
7.根据所给信息,请你求出每只玩具小猫和玩具小狗的价格(单位:元)分别为( )
A.20,10 B.15,20 C.10,30 D.8,26
8.如图,长方形ABCD中放置9个形状、大小都相同的小长方形,相关数据如图中所示,则图中阴影部分的面积为( )
A.18 B.20 C.22 D.24C
9.明代数学家程大位所著的《算法统宗》中有这样一道题:有83000根短竹,每根短竹可制成毛笔的笔管3个或笔套5个,怎样安排用于制作笔管或笔套的短竹的数量,使制成的1个笔管与1个笔套正好配套?设用于制作笔管的短竹数为x根,用于制作笔套的短竹数为y根,可列方程组为______.
10.茶叶作为浙江省农业十大主导产业之一,是助力乡村振兴的民生产业.某村有土地60公顷,计划将其中10%的土地种植蔬菜,其余的土地开辟为茶园和种植粮食.已知茶园的面积比种粮食面积的2倍少3公顷,问茶园和种粮食的面积各多少公顷?设茶园的面积为x公顷,种粮食的面积为y公顷,可列方程组为___________.
11.《孙子算经》是中国古代重要的数学著作,成书大约在一千五百年前.书中记载了一个数学问题:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”其大意是:“用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,绳子比长木短1尺,问长木多少尺?”设绳长x尺,木长y尺,可列方程组为_______________.
12.有若干张如图①所示的拼图卡,用3张这样的拼图卡按图②的方式无缝隙拼接在一起,拼成的图案总长为;如图③,用8张这样的拼图卡按同样的方式拼接,拼成的图案总长为;若用x张这样的拼图卡按同样的方式拼接,拼成的图案总长为,则y与x之间的函数关系式为_________(x为正整数).
13.一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车.已知过去两次租用这两种货车的情况如下表:
第一次 第二次
甲种货车辆数(辆) 2 5
乙种货车辆数(辆) 3 6
累计运货吨数(吨) 15.5 35
现租用该公司3辆甲种货车及5辆乙种货车一次刚好运完这批货,如果按每吨付运费30元计算,问货主应付运费多少元?
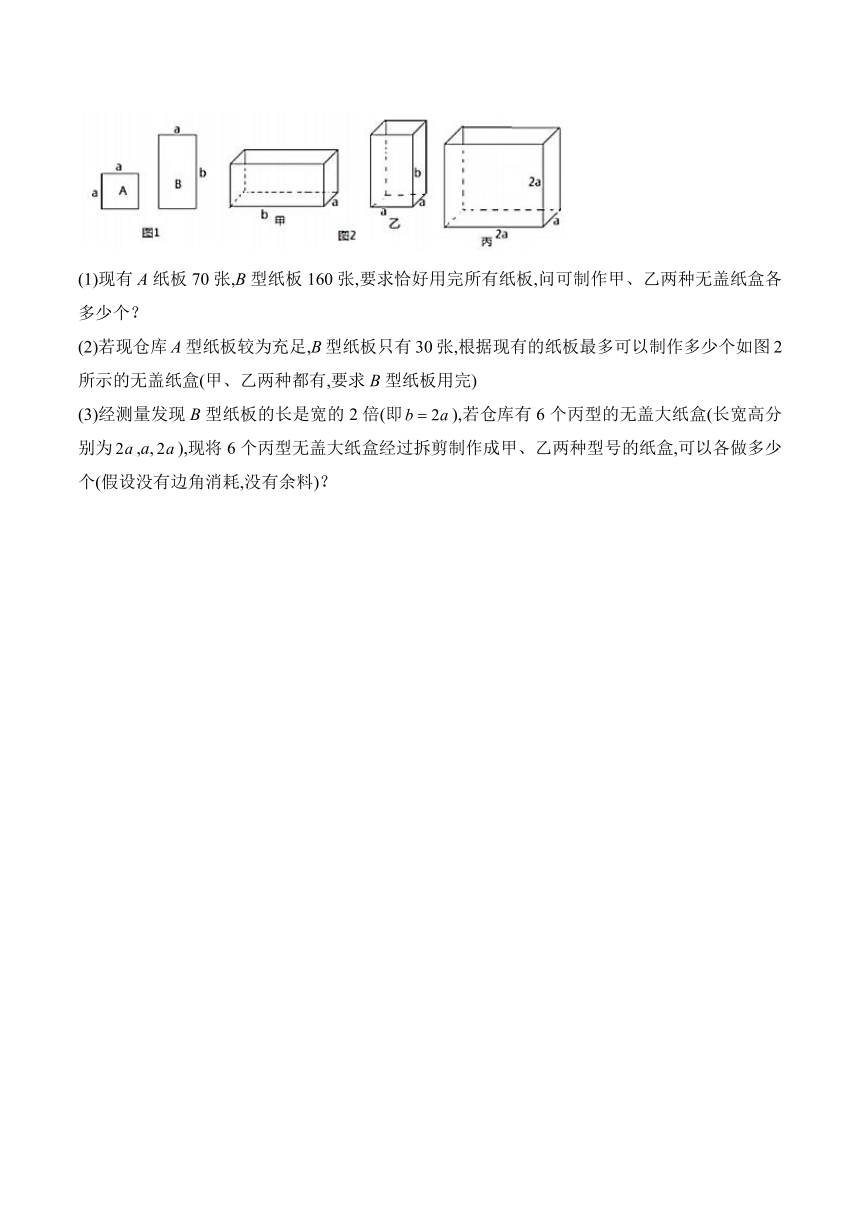
14.用如图1所示的A,B两种纸板作侧面或底面制作如图2所示的甲、乙两种长方体形状的无盖纸盒.
(1)现有A纸板70张,B型纸板160张,要求恰好用完所有纸板,问可制作甲、乙两种无盖纸盒各多少个?
(2)若现仓库A型纸板较为充足,B型纸板只有30张,根据现有的纸板最多可以制作多少个如图2所示的无盖纸盒(甲、乙两种都有,要求B型纸板用完)
(3)经测量发现B型纸板的长是宽的2倍(即),若仓库有6个丙型的无盖大纸盒(长宽高分别为,a,),现将6个丙型无盖大纸盒经过拆剪制作成甲、乙两种型号的纸盒,可以各做多少个(假设没有边角消耗,没有余料)?
答案以及解析
1.答案:C
解析:设木长x尺,绳子长y尺,
∵用一根绳子去量一根长木,绳子还剩余4.5尺,
∴.
∵将绳子对折再量长木,长木还剩余l尺,
∴,
∴可列方程组为.
故选C.
2.答案:C
解析:∵两人一共投中30次,
∴;
∵小华投中1次得5分,爸爸投中1次得3分,爸爸比小华多得2分,
∴.
∴根据题意得可列二元一次方程组.
故选:C.
3.答案:A
解析:设学生有x人,树苗有y棵,根据题意可列出方程组:
,
故A正确.
故选:A.
4.答案:A
解析:设小长方形的宽为,长为,
根据题意得,,
解得,
一个小长方形的面积为.
故选:A.
5.答案:B
解析:设大容器的容积为x斛,小容器的容积为y斛,
根据题意得:.
故选:B.
6.答案:A
解析:设买了甜果x个,苦果y个,由题意,得:
;
故选A.
7.答案:C
解析:设每只小猫为x元,每只小狗为y元,由题意得
,
解之得.
每只小猫为10元,每只小狗为30元.
故选:C.
8.答案:A
解析:设小长方形的长为x,宽为y,
依题意,得:,解得
∴.
故选:A.
9.答案:
解析:设用于制作笔管的短竹数为x根,用于制作笔套的短竹数为y根,
由题意得:,
故答案为:.
10.答案:(变形后正确即可)
解析:根据“某村有土地60公顷,计划将其中的土地种植蔬菜”,可列方程为;根据“茶园的面积比种粮食面积的2倍少3公顷”,可列方程为.故该方程组为整理得
11.答案:
解析:根据题意可直接列出方程组:,
故答案为:.
12.答案:
解析:设每一个拼图卡长度为,重合部分长度为,则
,解得,
若用x张这样的拼图卡按同样的方式拼接,拼成的图案总长为,则y与x之间的函数关系式为,
故答案为:.
13.答案:货主应付运费735元
解析:设甲、乙两种货车载重量分别为x吨、y吨
根据题意得,
解得
答:货主应付运费735元.
14.答案:(1)制作甲24个,乙22个
(2)最多可以制作甲,乙纸盒9个
(3)制作甲6个,乙4个
解析:(1)设制作甲x个,乙y个,则
,
解得:,
即制作甲24个,乙22个.
(2)设制作甲m个,乙k个,则
,
消去k得,,
因为:m,n为正整数,
所以:,.
综上,最多可以制作甲,乙纸盒9个.
(3)因为1个丙型大纸盒可以拆成7块B型纸板,
所以6个丙型大纸盒可以拆成42块B型纸板,
而制作1个甲纸盒要4块B型纸板,制作1个乙纸盒要4.5块B型纸板,
设制作甲c个,乙d个,则,
因为c,d为正整数,所以,,
即可以制作甲6个,乙4个.
1.《孙子算经》中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,长木还剩余l尺,问木长多少尺?若设木长尺,绳子长尺,则可列方程组为( )
A. B. C. D.
2.小华和爸爸玩“掷飞镖”游戏.游戏规则:小华投中1次得5分,爸爸投中1次得3分,两人一共投中30次.经过计算发现爸爸比小华多得2分.设小华投中的次数为x,爸爸投中的次数为y,根据题意列出的方程组正确的是( )
A. B. C. D.
3.若干名学生一起去种树,如果每人种4棵,则还剩下3棵树苗;如果每人种5棵,则缺少5棵树苗,设学生有x人,树苗有y棵,根据题意可列出方程组( )
A. B. C. D.
4.如图,宽为的矩形图案是由10个形状和大小完全一样的小长方形拼成,则一个小长方形的面积为( )
A. B. C. D.
5.《九章算术》中有一题:“今有大器五、小器一容三斛;大器一、小器五容二斛.问大、小器各容几何?”译文:今有大容器5个,小容器1个,总容量为3斛(斛:古代容是单位);大容器1个,小容器5个,总容暴为2斛.问大容器、小容器的容量各是多少斛?设大容器的容量为x斛,小容器的容量为y斛,则可列方程组是( )
A. B. C. D.
6.数学家朱世杰所著的《四元玉鉴》是中国元代重要的数学著作之一,书中记载着这样一个问题,大意是:999文钱买了周果和苦果共1000个,11文钱可买9个甜果,4文钱可买7个苦果,问甜果,苦果各买了多少个?设买了甜果x个,苦果y个,则可列方程组为( )
A. B. C. D.
7.根据所给信息,请你求出每只玩具小猫和玩具小狗的价格(单位:元)分别为( )
A.20,10 B.15,20 C.10,30 D.8,26
8.如图,长方形ABCD中放置9个形状、大小都相同的小长方形,相关数据如图中所示,则图中阴影部分的面积为( )
A.18 B.20 C.22 D.24C
9.明代数学家程大位所著的《算法统宗》中有这样一道题:有83000根短竹,每根短竹可制成毛笔的笔管3个或笔套5个,怎样安排用于制作笔管或笔套的短竹的数量,使制成的1个笔管与1个笔套正好配套?设用于制作笔管的短竹数为x根,用于制作笔套的短竹数为y根,可列方程组为______.
10.茶叶作为浙江省农业十大主导产业之一,是助力乡村振兴的民生产业.某村有土地60公顷,计划将其中10%的土地种植蔬菜,其余的土地开辟为茶园和种植粮食.已知茶园的面积比种粮食面积的2倍少3公顷,问茶园和种粮食的面积各多少公顷?设茶园的面积为x公顷,种粮食的面积为y公顷,可列方程组为___________.
11.《孙子算经》是中国古代重要的数学著作,成书大约在一千五百年前.书中记载了一个数学问题:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”其大意是:“用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,绳子比长木短1尺,问长木多少尺?”设绳长x尺,木长y尺,可列方程组为_______________.
12.有若干张如图①所示的拼图卡,用3张这样的拼图卡按图②的方式无缝隙拼接在一起,拼成的图案总长为;如图③,用8张这样的拼图卡按同样的方式拼接,拼成的图案总长为;若用x张这样的拼图卡按同样的方式拼接,拼成的图案总长为,则y与x之间的函数关系式为_________(x为正整数).
13.一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车.已知过去两次租用这两种货车的情况如下表:
第一次 第二次
甲种货车辆数(辆) 2 5
乙种货车辆数(辆) 3 6
累计运货吨数(吨) 15.5 35
现租用该公司3辆甲种货车及5辆乙种货车一次刚好运完这批货,如果按每吨付运费30元计算,问货主应付运费多少元?
14.用如图1所示的A,B两种纸板作侧面或底面制作如图2所示的甲、乙两种长方体形状的无盖纸盒.
(1)现有A纸板70张,B型纸板160张,要求恰好用完所有纸板,问可制作甲、乙两种无盖纸盒各多少个?
(2)若现仓库A型纸板较为充足,B型纸板只有30张,根据现有的纸板最多可以制作多少个如图2所示的无盖纸盒(甲、乙两种都有,要求B型纸板用完)
(3)经测量发现B型纸板的长是宽的2倍(即),若仓库有6个丙型的无盖大纸盒(长宽高分别为,a,),现将6个丙型无盖大纸盒经过拆剪制作成甲、乙两种型号的纸盒,可以各做多少个(假设没有边角消耗,没有余料)?
答案以及解析
1.答案:C
解析:设木长x尺,绳子长y尺,
∵用一根绳子去量一根长木,绳子还剩余4.5尺,
∴.
∵将绳子对折再量长木,长木还剩余l尺,
∴,
∴可列方程组为.
故选C.
2.答案:C
解析:∵两人一共投中30次,
∴;
∵小华投中1次得5分,爸爸投中1次得3分,爸爸比小华多得2分,
∴.
∴根据题意得可列二元一次方程组.
故选:C.
3.答案:A
解析:设学生有x人,树苗有y棵,根据题意可列出方程组:
,
故A正确.
故选:A.
4.答案:A
解析:设小长方形的宽为,长为,
根据题意得,,
解得,
一个小长方形的面积为.
故选:A.
5.答案:B
解析:设大容器的容积为x斛,小容器的容积为y斛,
根据题意得:.
故选:B.
6.答案:A
解析:设买了甜果x个,苦果y个,由题意,得:
;
故选A.
7.答案:C
解析:设每只小猫为x元,每只小狗为y元,由题意得
,
解之得.
每只小猫为10元,每只小狗为30元.
故选:C.
8.答案:A
解析:设小长方形的长为x,宽为y,
依题意,得:,解得
∴.
故选:A.
9.答案:
解析:设用于制作笔管的短竹数为x根,用于制作笔套的短竹数为y根,
由题意得:,
故答案为:.
10.答案:(变形后正确即可)
解析:根据“某村有土地60公顷,计划将其中的土地种植蔬菜”,可列方程为;根据“茶园的面积比种粮食面积的2倍少3公顷”,可列方程为.故该方程组为整理得
11.答案:
解析:根据题意可直接列出方程组:,
故答案为:.
12.答案:
解析:设每一个拼图卡长度为,重合部分长度为,则
,解得,
若用x张这样的拼图卡按同样的方式拼接,拼成的图案总长为,则y与x之间的函数关系式为,
故答案为:.
13.答案:货主应付运费735元
解析:设甲、乙两种货车载重量分别为x吨、y吨
根据题意得,
解得
答:货主应付运费735元.
14.答案:(1)制作甲24个,乙22个
(2)最多可以制作甲,乙纸盒9个
(3)制作甲6个,乙4个
解析:(1)设制作甲x个,乙y个,则
,
解得:,
即制作甲24个,乙22个.
(2)设制作甲m个,乙k个,则
,
消去k得,,
因为:m,n为正整数,
所以:,.
综上,最多可以制作甲,乙纸盒9个.
(3)因为1个丙型大纸盒可以拆成7块B型纸板,
所以6个丙型大纸盒可以拆成42块B型纸板,
而制作1个甲纸盒要4块B型纸板,制作1个乙纸盒要4.5块B型纸板,
设制作甲c个,乙d个,则,
因为c,d为正整数,所以,,
即可以制作甲6个,乙4个.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
