八年级数学北师大版(2012)上册 5.5应用二元一次方程组—里程碑上的数——课时优化训练(含详解)
文档属性
| 名称 | 八年级数学北师大版(2012)上册 5.5应用二元一次方程组—里程碑上的数——课时优化训练(含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 344.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-14 13:21:02 | ||
图片预览


文档简介
5.5应用二元一次方程组—里程碑上的数——八年级数学北师大版(2012)上册课时优化训练
1.小张家在小王家西边100米,他们同时从各自家里出发,前往小张家西边的博物馆.设小张每分钟走x米,小王每分钟走y米,如果出发10分钟后两人同时到达了博物馆,并且小张3分钟行走的路程比小王5分钟行走的路程少210米,则可列方程组( )
A. B. C. D.
2.A地至B地的航线长1200千米,一艘轮船从A地顺水开往B地需30小时,它逆水返回需要40小时,设轮船在静水中的速度为x千米/小时,水速为y千米/小时,可列方程组( )
A. B.
C. D.
3.小明、小华两人练习跑步,如果小华先跑,则小明跑就可追上他;如果小华先跑,则小明跑就可追上他,若设小明的速度为,小华的速度为,则下列符合题意的方程组是( )
A. B.
C. D.
4.作业本中有这样一道题:“小明去郊游,上午8时30分从家中出发,先走平路,然后登山,中午12时到达山顶,原地休息后沿原路返回,正好下午3时到家.若他平路每小时走,登山每小时走,下山每小时走,求小明家到山顶的路程.”小李查看解答时发现答案中的方程组中有污损:则答案中另一个方程应为( )
A. B.
C. D.
5.从甲地到乙地有一段上坡与一段平路,如果保持上坡每小时走3km,平路每小时走4km.下坡每小时走5km,那么从甲地到乙地需54min,从乙地到甲地需42min.设从甲地到乙地的上坡路程长xkm,平路路程长为ykm,依题意列方程组正确的是( )
A. B. C. D.
6.“悟空顺风探妖踪,千里只用五分钟;归时五分行六百,试问风速是多少?”大致意思是:孙悟空追寻妖精的行踪,去时顺风,1000里只用了5分钟:回来时逆风,5分钟只走了600里,试求风的速度是每分钟多少里?( )
A.30 B.40 C.50 D.60
7.小明和小亮练习赛跑,如果小明让小亮先跑2秒,那么小明跑6秒就追上小亮,如果小明让小亮先跑16米,那么小明跑8秒就追上小亮.则小明和小亮每秒跑的路程分别为( )
A.6米,4米 B.10米,8米 C.8米,6米 D.6米,8米
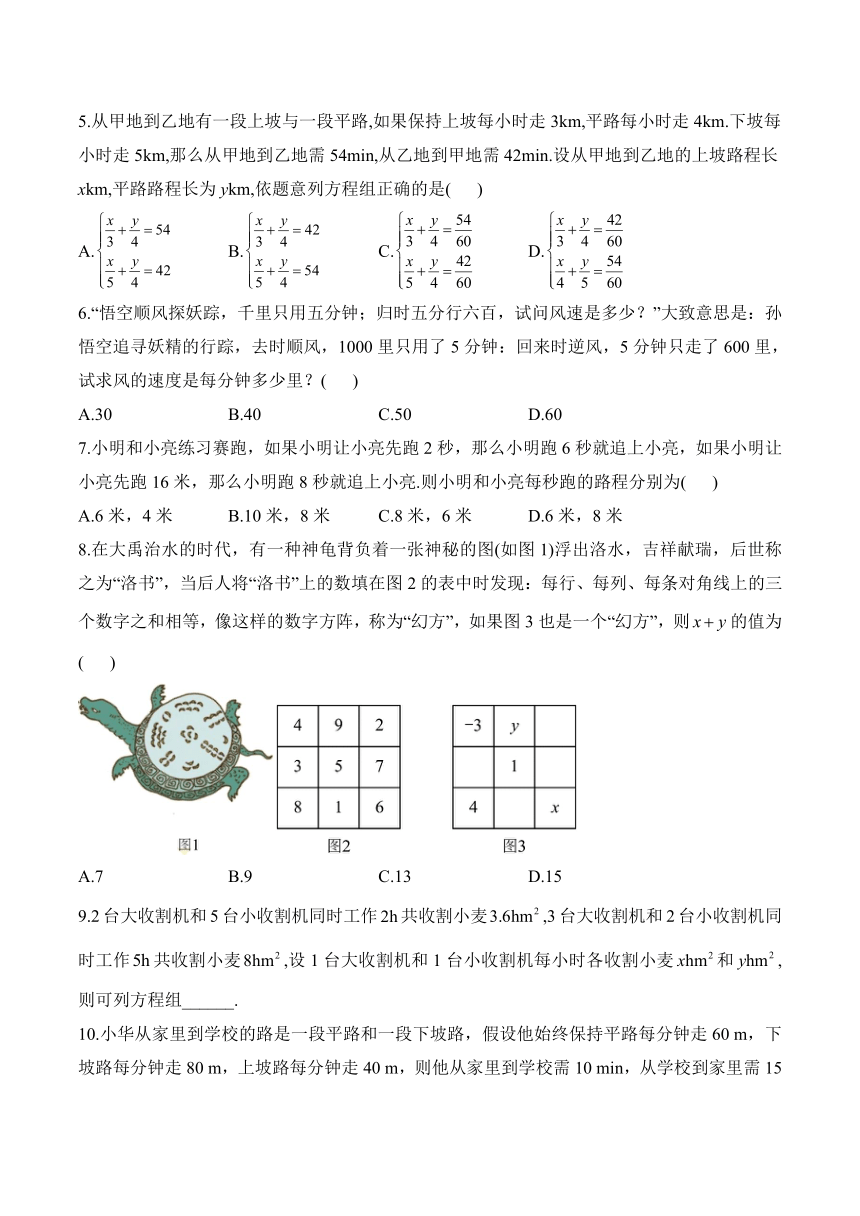
8.在大禹治水的时代,有一种神龟背负着一张神秘的图(如图1)浮出洛水,吉祥献瑞,后世称之为“洛书”,当后人将“洛书”上的数填在图2的表中时发现:每行、每列、每条对角线上的三个数字之和相等,像这样的数字方阵,称为“幻方”,如果图3也是一个“幻方”,则的值为( )
A.7 B.9 C.13 D.15
9.2台大收割机和5台小收割机同时工作共收割小麦,3台大收割机和2台小收割机同时工作共收割小麦,设1台大收割机和1台小收割机每小时各收割小麦和,则可列方程组______.
10.小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60 m,下坡路每分钟走80 m,上坡路每分钟走40 m,则他从家里到学校需10 min,从学校到家里需15 min.设平路有,下坡路有,则可列方程组为__________.
11.一个两位数,个位数字比十位数字大5,如果把个位数字与十位数字对调,那么所得到的新数与原数的和是99,这个数为________.
12.甲、乙两工程队共同修建150 km的公路,原计划30个月完工.实际施工时,甲队通过技术创新,施工效率提高了50%,乙队施工效率不变,结果提前5个月完工.甲、乙两工程队原计划平均每月分别修建公路___________km,___________km.
13.一艘轮船在相距的甲、乙两地之间匀速航行,从甲地到乙地顺流航行用了,从乙地到甲地逆流航行用了.(请列方程组解答)
(1)求这艘轮船在静水中的速度和水流速度;
(2)若在甲、乙两地之间的丙地新建一个码头,使该轮船从甲地到丙地和从乙地到丙地所用的航行时间相同,问甲、丙两地相距多少千米?
14.某两位数,两个数位上的数之和为.这个两位数加上,得到的两位数恰好等于原两位数的两个数字交换位置所表示的数,求原两位数.
(1)列一元一次方程求解.
(2)如果设原两位数的十位数字为,个位数字为,列二元一次方程组.
(3)检验(1)中求得的结果是否满足(2)中的方程组.
答案以及解析
1.答案:A
解析:设小张每分钟走x米,小王每分钟走y米,
由题意得,,
故选A.
2.答案:B
解析:设轮船在静水中的平均速度为x千米/小时,水速为y千米/小时,则:
船顺水行驶速度为:千米/小时.
船顺水行驶速度为:千米/小时.
依题意,得:.
故选:B.
3.答案:D
解析:依题意得:,
即,
故选:D.
4.答案:D
5.答案:C
解析:设从甲地到乙地上坡与平路分别为xkm,ykm,
由题意得:,
故选:C.
6.答案:B
解析:设孙悟空的速度为x里/分钟,风速为y里/分钟,
依题意,得
解得
答:风的速度为40里/分钟.
故选B.
7.答案:C
解析:设小明的速度为x米/秒,小亮的速度为y米/秒,则
,解得,
小明和小亮每秒跑的路程分别为8米,6米,
故选:C.
8.答案:C
解析:根据题意得:,
解得:,
.
故选:C.
9.答案:
解析:由“2台大收割机和5台小收割机同时工作共收割小麦”可得:,
由“3台大收割机和2台小收割机同时工作共收割小麦”可得:,
因此可列方程组:,
故答案为:.
10.答案:(变形后正确即可)
解析:小华从家到学校时,平路需要的时间为,下坡路需要的时间为;从学校回家时,上坡路需要的时间为,平路需要的时间为.所以可列方程组为
11.答案:27
解析:设个位数字为x,十位数字为y,
由题意,得,
解得:,
即原来的两位数是27.
故答案为:27.
12.答案:2;3
解析:设甲工程队原计划平均每月修建公路,乙工程队原计划平均每月修建公路,根据题意,得解得
13.答案:(1)这艘轮船在静水中的速度是,水流速度是
(2)甲、丙两地相距
解析:(1)设这艘轮船在静水中的速度是,水流速度是.
依题意,得解得
答:这艘轮船在静水中的速度是,水流速度是.
(2)设甲、丙两地相距,则乙、丙两地相距.
依题意,得,解得.
答:甲、丙两地相距.
14.答案:(1)原两位数为38
(2)
(3)(1)中求得的结果满足(2)中的方程组
解析:(1)设原两位数的个位数字为,则十位数字为,
依题意,得:,
解得:,
∴.
答:原两位数为38;
(2)设原两位数的十位数字为,个位数字为,
依题意,得:;
(3)结合(1)可知,,,
∴,,
∴(1)中求得的结果满足(2)中的方程组.
1.小张家在小王家西边100米,他们同时从各自家里出发,前往小张家西边的博物馆.设小张每分钟走x米,小王每分钟走y米,如果出发10分钟后两人同时到达了博物馆,并且小张3分钟行走的路程比小王5分钟行走的路程少210米,则可列方程组( )
A. B. C. D.
2.A地至B地的航线长1200千米,一艘轮船从A地顺水开往B地需30小时,它逆水返回需要40小时,设轮船在静水中的速度为x千米/小时,水速为y千米/小时,可列方程组( )
A. B.
C. D.
3.小明、小华两人练习跑步,如果小华先跑,则小明跑就可追上他;如果小华先跑,则小明跑就可追上他,若设小明的速度为,小华的速度为,则下列符合题意的方程组是( )
A. B.
C. D.
4.作业本中有这样一道题:“小明去郊游,上午8时30分从家中出发,先走平路,然后登山,中午12时到达山顶,原地休息后沿原路返回,正好下午3时到家.若他平路每小时走,登山每小时走,下山每小时走,求小明家到山顶的路程.”小李查看解答时发现答案中的方程组中有污损:则答案中另一个方程应为( )
A. B.
C. D.
5.从甲地到乙地有一段上坡与一段平路,如果保持上坡每小时走3km,平路每小时走4km.下坡每小时走5km,那么从甲地到乙地需54min,从乙地到甲地需42min.设从甲地到乙地的上坡路程长xkm,平路路程长为ykm,依题意列方程组正确的是( )
A. B. C. D.
6.“悟空顺风探妖踪,千里只用五分钟;归时五分行六百,试问风速是多少?”大致意思是:孙悟空追寻妖精的行踪,去时顺风,1000里只用了5分钟:回来时逆风,5分钟只走了600里,试求风的速度是每分钟多少里?( )
A.30 B.40 C.50 D.60
7.小明和小亮练习赛跑,如果小明让小亮先跑2秒,那么小明跑6秒就追上小亮,如果小明让小亮先跑16米,那么小明跑8秒就追上小亮.则小明和小亮每秒跑的路程分别为( )
A.6米,4米 B.10米,8米 C.8米,6米 D.6米,8米
8.在大禹治水的时代,有一种神龟背负着一张神秘的图(如图1)浮出洛水,吉祥献瑞,后世称之为“洛书”,当后人将“洛书”上的数填在图2的表中时发现:每行、每列、每条对角线上的三个数字之和相等,像这样的数字方阵,称为“幻方”,如果图3也是一个“幻方”,则的值为( )
A.7 B.9 C.13 D.15
9.2台大收割机和5台小收割机同时工作共收割小麦,3台大收割机和2台小收割机同时工作共收割小麦,设1台大收割机和1台小收割机每小时各收割小麦和,则可列方程组______.
10.小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60 m,下坡路每分钟走80 m,上坡路每分钟走40 m,则他从家里到学校需10 min,从学校到家里需15 min.设平路有,下坡路有,则可列方程组为__________.
11.一个两位数,个位数字比十位数字大5,如果把个位数字与十位数字对调,那么所得到的新数与原数的和是99,这个数为________.
12.甲、乙两工程队共同修建150 km的公路,原计划30个月完工.实际施工时,甲队通过技术创新,施工效率提高了50%,乙队施工效率不变,结果提前5个月完工.甲、乙两工程队原计划平均每月分别修建公路___________km,___________km.
13.一艘轮船在相距的甲、乙两地之间匀速航行,从甲地到乙地顺流航行用了,从乙地到甲地逆流航行用了.(请列方程组解答)
(1)求这艘轮船在静水中的速度和水流速度;
(2)若在甲、乙两地之间的丙地新建一个码头,使该轮船从甲地到丙地和从乙地到丙地所用的航行时间相同,问甲、丙两地相距多少千米?
14.某两位数,两个数位上的数之和为.这个两位数加上,得到的两位数恰好等于原两位数的两个数字交换位置所表示的数,求原两位数.
(1)列一元一次方程求解.
(2)如果设原两位数的十位数字为,个位数字为,列二元一次方程组.
(3)检验(1)中求得的结果是否满足(2)中的方程组.
答案以及解析
1.答案:A
解析:设小张每分钟走x米,小王每分钟走y米,
由题意得,,
故选A.
2.答案:B
解析:设轮船在静水中的平均速度为x千米/小时,水速为y千米/小时,则:
船顺水行驶速度为:千米/小时.
船顺水行驶速度为:千米/小时.
依题意,得:.
故选:B.
3.答案:D
解析:依题意得:,
即,
故选:D.
4.答案:D
5.答案:C
解析:设从甲地到乙地上坡与平路分别为xkm,ykm,
由题意得:,
故选:C.
6.答案:B
解析:设孙悟空的速度为x里/分钟,风速为y里/分钟,
依题意,得
解得
答:风的速度为40里/分钟.
故选B.
7.答案:C
解析:设小明的速度为x米/秒,小亮的速度为y米/秒,则
,解得,
小明和小亮每秒跑的路程分别为8米,6米,
故选:C.
8.答案:C
解析:根据题意得:,
解得:,
.
故选:C.
9.答案:
解析:由“2台大收割机和5台小收割机同时工作共收割小麦”可得:,
由“3台大收割机和2台小收割机同时工作共收割小麦”可得:,
因此可列方程组:,
故答案为:.
10.答案:(变形后正确即可)
解析:小华从家到学校时,平路需要的时间为,下坡路需要的时间为;从学校回家时,上坡路需要的时间为,平路需要的时间为.所以可列方程组为
11.答案:27
解析:设个位数字为x,十位数字为y,
由题意,得,
解得:,
即原来的两位数是27.
故答案为:27.
12.答案:2;3
解析:设甲工程队原计划平均每月修建公路,乙工程队原计划平均每月修建公路,根据题意,得解得
13.答案:(1)这艘轮船在静水中的速度是,水流速度是
(2)甲、丙两地相距
解析:(1)设这艘轮船在静水中的速度是,水流速度是.
依题意,得解得
答:这艘轮船在静水中的速度是,水流速度是.
(2)设甲、丙两地相距,则乙、丙两地相距.
依题意,得,解得.
答:甲、丙两地相距.
14.答案:(1)原两位数为38
(2)
(3)(1)中求得的结果满足(2)中的方程组
解析:(1)设原两位数的个位数字为,则十位数字为,
依题意,得:,
解得:,
∴.
答:原两位数为38;
(2)设原两位数的十位数字为,个位数字为,
依题意,得:;
(3)结合(1)可知,,,
∴,,
∴(1)中求得的结果满足(2)中的方程组.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
