浙教版数学九年级上册 期末测试卷(含答案)
文档属性
| 名称 | 浙教版数学九年级上册 期末测试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 897.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-15 00:00:00 | ||
图片预览


文档简介
期末测试卷
班级 学号 得分 姓名
一、选择题(本大题有10小题,每小题3分,共30分)
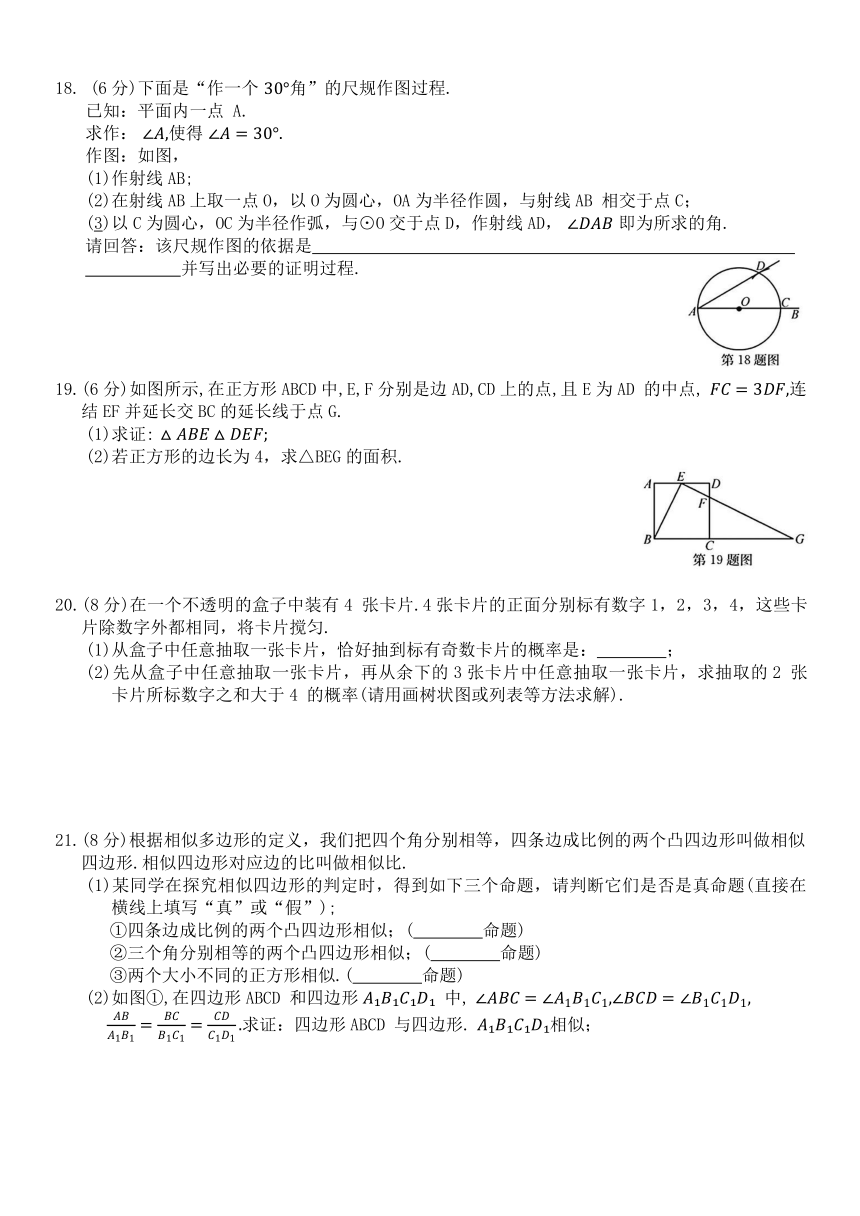
1. 已知2x=3y,那么xy等于( )
A. 2 B. 3 C D
2. 在一个不透明的盒子里,装有4个黑球和若干个白球,它们除颜色外没有任何其他区别,摇匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复,共摸球40次,其中10次摸到黑球,则估计盒子中大约有白球( )
A. 12个 B. 16 个 C. 20个 D. 30个
3.如图,AB是⊙O的直径,点C,D是圆上两点,且∠AOC=126°,则∠CDB=( )
A. 54° B. 64° C. 27° D. 37°
4. 抛物线. 可以由抛物线 平移而得到,下列平移正确的是( )
A. 先向左平移2个单位,然后向上平移1个单位
B. 先向左平移2个单位,然后向下平移1个单位
C. 先向右平移2个单位,然后向上平移1个单位
D. 先向右平移2个单位,然后向下平移1个单位
5. 如图,在 ABCD中,点E在对角线BD 上,EM∥AD,交AB于点M,EN∥AB,交AD于点N,则下列式子一定正确的是( )
6. 将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是( )
7. 若二次函数. 的图象经过点(-2,0),则关于x的方程。 的实数根为 ( )
8. 如图,Rt△OAB的顶点A(-2,4)在抛物线. 上,将Rt△OAB绕点O 顺时针旋转90°,得到 △OCD,边CD与该抛物线交于点P,则点P的坐标为( )
B. (2,2) D. (2 )
9. 如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB 的中点,P 是直径AB上的一动点,若MN=1,则△PMN周长的最小值为( )
A. 4 B. 5 C. 6 D. 7
10.如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形 ABCD 与正方形EFGH.连结EG,BD 相交于点O、BD与HC 相交于点P.若GO=GP,则S正方形ABCD白的值是( )
D
二、填空题(本大题有6小题,每小题4分,共24分)
11. 某物体从上午7时至下午4时的温度M(℃)是时间t(h)的函数: 其中t=0 表示中午 12(时,t=1表示下午1时),则上午10时此物体的温度是 ℃.
12. 某射手在相同条件下进行射击训练,结果如下表:
射击次数n 10 20 40 50 100 200 500 1000
击中靶心的频数m 9 19 37 45 89 181 449 901
击中靶心的频率m 0.900 0.950 0.925 0.900 0.890 0.905 0.898 0.901
该射手击中靶心的概率的估计值是 (精确到0.01).
13. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,将 Rt△ABC绕点A 逆时针旋转 30°后得到 Rt△ADE,点 B经过的路径为 ,则图中阴影部分的面积是 .
14. 如图,在△ABC中,DE∥BC,DE分别交AB,AC于点D,E,且AD:AB=1:2,若△ADE的面积为2,则S△ABC= .
15. 操场上有一棵树,数学兴趣小组的同学们想利用树影测量树高,在阳光下他们测得一根长为1m的直立竹竿的影长是1.5m,此时,测得树的影长为16.5m,则树高为 m.
16. 已知抛物线 的对称轴为直线l,如果点 M(-3,0)与点 N关于直线l对称,那么点 N 的坐标是 .
三、解答题(本大题有8小题,共66分)
17.(6分)如图,在平面直角坐标系中,二次函数. 图象的顶点是A,与x轴交于B,C两点,与y轴交于点D.点 B的坐标是(1,0).
(1)求A,C两点的坐标,并根据图象直接写出当y>0时x的取值范围.
(2)平移该二次函数的图象,使点 D恰好落在点 A 的位置上,求平移后图象所对应的二次函数的表达式.
18. (6分)下面是“作一个 角”的尺规作图过程.
已知:平面内一点 A.
求作: 使得
作图:如图,
(1)作射线AB;
(2)在射线AB上取一点O,以O为圆心,OA为半径作圆,与射线AB 相交于点C;
(3)以C为圆心,OC为半径作弧,与⊙O交于点D,作射线AD, 即为所求的角.
请回答:该尺规作图的依据是 并写出必要的证明过程.
19.(6分)如图所示,在正方形ABCD中,E,F分别是边AD,CD上的点,且E为AD 的中点, 连结EF并延长交BC的延长线于点G.
(1)求证:
(2)若正方形的边长为4,求△BEG的面积.
20.(8分)在一个不透明的盒子中装有4 张卡片.4张卡片的正面分别标有数字1,2,3,4,这些卡片除数字外都相同,将卡片搅匀.
(1)从盒子中任意抽取一张卡片,恰好抽到标有奇数卡片的概率是: ;
(2)先从盒子中任意抽取一张卡片,再从余下的3张卡片中任意抽取一张卡片,求抽取的2 张卡片所标数字之和大于4 的概率(请用画树状图或列表等方法求解).
21.(8分)根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形.相似四边形对应边的比叫做相似比.
(1)某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否是真命题(直接在横线上填写“真”或“假”);
①四条边成比例的两个凸四边形相似;( 命题)
②三个角分别相等的两个凸四边形相似;( 命题)
③两个大小不同的正方形相似.( 命题)
(2)如图①,在四边形ABCD 和四边形 中,
求证:四边形ABCD 与四边形. 相似;
(3)如图②,四边形ABCD中,AB∥CD,AC与BD 相交于点O,过点O作. 分别交AD,BC于点E,F.记四边形ABFE的面积为S ,四边形EFCD的面积为( ,若四边形ABFE 与四边形EFCD 相似,求 的值.
22.(10分)如图,在Rt△ABC中,M是斜边AB 的中点,以CM为直径作圆O交AC 于点 N,延长 MN 至点D,使 ND=MN,连结AD,CD,CD交圆O于点E,连结 NE.
(1)判断四边形 AMCD的形状,并说明理由;
(2)求证:ND=NE;
(3)若DE=2,EC=3,求 BC的长.
23.(10分)如图1,排球场长为18m,宽为9m,网高为2.24m.队员站在底线O点处发球,球从点O的正上方1.9m的C 点发出,运动路线是抛物线的一部分,当球运动到最高点 A 时,高度为 2.88m.即BA=2.88m.这时水平距离OB=7m,以直线OB为x轴,直线OC为y轴,建立平面直角坐标系,如图2.(1)若球向正前方运动(即x轴垂直于底线),求球运动的高度y(m)与水平距离x(m)之间的函数关系式(不必写出x取值范围).并判断这次发球能否过网 是否出界 说明理由;
(2)若球过网后的落点是对方场地①号位内的点 P(如图1,点P距底线1m,边线0.5m),问发球点O在底线上的哪个位置 (参考数据 取1.4)
24.(12分)如图,在△ABC中,∠ACB=90°,将△ABC沿直线AB 翻折得到△ABD,连结CD交AB 于点M. E是线段CM上的点,连结 BE. F 是△BDE的外接圆与AD 的另一个交点,连结 EF,BF.
(1)求证: 是直角三角形;
(2)求证:
(3)当AB=6,BC=m时,在线段CM上存在点E,使得EF和AB 互相平分,求m的值.
期末测试卷
D 2. A 3. C 4. D 5. D 6. A 7. A8. C 9. B 10. B 11. 114 12. 0.90 13 14. 8 15. 11 16. (1,0)
17. 解:(1)把 B(1,0)代入 得0=a+4 解得 +1,∴点A的坐标为(2,1),∵抛物线的对称轴为直线x=2,且点C与点B 关于对称轴对称,∴点 C的坐标为(3,0),∴当y>0时,x的取值范围是1(2)∵D(0,-3),∴点D移到点 A 时,抛物线向右平移2个单位,向上平移4个单位,平移后所得的图象对应的函数的表达式为
18. 解:作图的依据是:直径所对的圆周角是直角,等边三角形的每个内角为 60°,直角三角形两锐角互余等.如图,连结OD,CD.由作图可知:OD= OC = CD,∴△ODC是等边三角形,
∴∠DCO=60°,∵AC 是⊙O直 径, ∴ ∠ADC = 90°,
19. (1)证明:设正方形的边长为4a,∵E为AD 的中点,∴AE=ED=2a,∵FC=3DF,∴DF=a,FC= 又∠A=∠D=90°,∴△ABE∽△DEF.
(2)解:∵AD=4,∴DE=2,∵AD∥BC,∴△EDF∽△GCF,∴ ∴△BEG的面积
20.(1)
卡1 卡2 1 2 3 4
1 3 4 5
2 3 5 6
3 4 5 7
4 5 6 7
由表知,一共有12种等可能情况,其中抽取的两数之和大于4的情况有8种, 即抽取的2张卡片所标数字之和大于4的概率为
21. (1)假 假 真 (2)证明:连结 BD,B D .∵ 且 ∴四边形ABCD与四边形. 相似.
(3)解:∵四边形 ABFE 与四边形 EFCD 相似,
22. (1)解:四边形 AMCD 是菱形.理由如下:∵M是 中AB 边的中点, 为⊙O的直径, =CN,∵ND=MN,∴四边形AMCD是菱形.
(2)证明:∵四边形CENM为⊙O的内接四边形,∴∠CEN+∠CMN=180°,∵∠CEN+∠DEN=180°,∴∠CMN=∠DEN,∵四边形 AMCD是菱形,∴CD=CM,∴∠CDM=∠CMN,∴∠DEN=∠CDM,∴ ND= NE. (3)解:∵∠CMN =∠DEN,∠MDC=∠EDN,∴△MDC∽△EDN, 设 DN=x,则MD=2x,由此得 解得: 或x= (不合题意,舍去),∴ 易知 MN 为△ABC的中位线,∴BC=
23. 解:(1)设抛物线的表达式为: 把(0,1.9)代入,得 解得 .抛物线的表达式为 2.88.当x=9时,
2.24,当x=18时, >0,故这次发球过网,但是出界了.
(2)分别过点 P,Q作底线、边线的平行线 PQ,OQ 交 于 点 Q, 则 在 Rt△OPQ中,OQ=18-1=17,当y=0时, 解得x=19或x=-5(其中. -5舍去).∴OP=19,而 OQ=17,故 8.4.∵9-8.4-0.5=0.1,∴发球点O右底线⊥l距右边线0.1m处.
24. (1)证明:∵△ABD是由△ABC 翻折得到的,∴∠ADB = ∠ACB = 90°. ∵∠EF., ∠EDB,∠EBF=∠EDF,∴∠EFB+∠EBF=∠EDB+∠EDF=∠ADB=90°,
∴∠BEF=90°,∴△BEF是直角三角形.
(2)证明:由翻折得AC=AD,∵BC=BD,
∴∠BDC=∠BCD,
∵∠EFB=∠EDB,
∴∠EFB=∠BCD.
∵AC=AD,BC=BD,∴AB⊥CD,∴∠AMC=90°.∵∠BCD+∠ACD=∠ACD+∠CAB=90°,
∴∠BCD=∠CAB,∴∠BFE=∠CAB,
∵∠ACB=∠FEB=90°,∴△BEF∽△BCA.
(3)解:设EF 交 AB 于点J.连结AE,如图.∵EF 与AB 互相平分,∴四边形 AFBE是平行四边形,∴BE∥AF,∴∠EFA=∠FEB=90°,即EF⊥AD.
∵BD⊥AD,∴EF∥BD,∵AJ=JB,∴AF=DF,∴FJ BD=π/ ∴EF=m,∵△ABC∽△CBM,∴BC: MB=AB: BC,∴BM= ,∵△BEJ∽△BME,∴BE 即 解得 (负根 已经舍弃).
班级 学号 得分 姓名
一、选择题(本大题有10小题,每小题3分,共30分)
1. 已知2x=3y,那么xy等于( )
A. 2 B. 3 C D
2. 在一个不透明的盒子里,装有4个黑球和若干个白球,它们除颜色外没有任何其他区别,摇匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复,共摸球40次,其中10次摸到黑球,则估计盒子中大约有白球( )
A. 12个 B. 16 个 C. 20个 D. 30个
3.如图,AB是⊙O的直径,点C,D是圆上两点,且∠AOC=126°,则∠CDB=( )
A. 54° B. 64° C. 27° D. 37°
4. 抛物线. 可以由抛物线 平移而得到,下列平移正确的是( )
A. 先向左平移2个单位,然后向上平移1个单位
B. 先向左平移2个单位,然后向下平移1个单位
C. 先向右平移2个单位,然后向上平移1个单位
D. 先向右平移2个单位,然后向下平移1个单位
5. 如图,在 ABCD中,点E在对角线BD 上,EM∥AD,交AB于点M,EN∥AB,交AD于点N,则下列式子一定正确的是( )
6. 将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是( )
7. 若二次函数. 的图象经过点(-2,0),则关于x的方程。 的实数根为 ( )
8. 如图,Rt△OAB的顶点A(-2,4)在抛物线. 上,将Rt△OAB绕点O 顺时针旋转90°,得到 △OCD,边CD与该抛物线交于点P,则点P的坐标为( )
B. (2,2) D. (2 )
9. 如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB 的中点,P 是直径AB上的一动点,若MN=1,则△PMN周长的最小值为( )
A. 4 B. 5 C. 6 D. 7
10.如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形 ABCD 与正方形EFGH.连结EG,BD 相交于点O、BD与HC 相交于点P.若GO=GP,则S正方形ABCD白的值是( )
D
二、填空题(本大题有6小题,每小题4分,共24分)
11. 某物体从上午7时至下午4时的温度M(℃)是时间t(h)的函数: 其中t=0 表示中午 12(时,t=1表示下午1时),则上午10时此物体的温度是 ℃.
12. 某射手在相同条件下进行射击训练,结果如下表:
射击次数n 10 20 40 50 100 200 500 1000
击中靶心的频数m 9 19 37 45 89 181 449 901
击中靶心的频率m 0.900 0.950 0.925 0.900 0.890 0.905 0.898 0.901
该射手击中靶心的概率的估计值是 (精确到0.01).
13. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,将 Rt△ABC绕点A 逆时针旋转 30°后得到 Rt△ADE,点 B经过的路径为 ,则图中阴影部分的面积是 .
14. 如图,在△ABC中,DE∥BC,DE分别交AB,AC于点D,E,且AD:AB=1:2,若△ADE的面积为2,则S△ABC= .
15. 操场上有一棵树,数学兴趣小组的同学们想利用树影测量树高,在阳光下他们测得一根长为1m的直立竹竿的影长是1.5m,此时,测得树的影长为16.5m,则树高为 m.
16. 已知抛物线 的对称轴为直线l,如果点 M(-3,0)与点 N关于直线l对称,那么点 N 的坐标是 .
三、解答题(本大题有8小题,共66分)
17.(6分)如图,在平面直角坐标系中,二次函数. 图象的顶点是A,与x轴交于B,C两点,与y轴交于点D.点 B的坐标是(1,0).
(1)求A,C两点的坐标,并根据图象直接写出当y>0时x的取值范围.
(2)平移该二次函数的图象,使点 D恰好落在点 A 的位置上,求平移后图象所对应的二次函数的表达式.
18. (6分)下面是“作一个 角”的尺规作图过程.
已知:平面内一点 A.
求作: 使得
作图:如图,
(1)作射线AB;
(2)在射线AB上取一点O,以O为圆心,OA为半径作圆,与射线AB 相交于点C;
(3)以C为圆心,OC为半径作弧,与⊙O交于点D,作射线AD, 即为所求的角.
请回答:该尺规作图的依据是 并写出必要的证明过程.
19.(6分)如图所示,在正方形ABCD中,E,F分别是边AD,CD上的点,且E为AD 的中点, 连结EF并延长交BC的延长线于点G.
(1)求证:
(2)若正方形的边长为4,求△BEG的面积.
20.(8分)在一个不透明的盒子中装有4 张卡片.4张卡片的正面分别标有数字1,2,3,4,这些卡片除数字外都相同,将卡片搅匀.
(1)从盒子中任意抽取一张卡片,恰好抽到标有奇数卡片的概率是: ;
(2)先从盒子中任意抽取一张卡片,再从余下的3张卡片中任意抽取一张卡片,求抽取的2 张卡片所标数字之和大于4 的概率(请用画树状图或列表等方法求解).
21.(8分)根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形.相似四边形对应边的比叫做相似比.
(1)某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否是真命题(直接在横线上填写“真”或“假”);
①四条边成比例的两个凸四边形相似;( 命题)
②三个角分别相等的两个凸四边形相似;( 命题)
③两个大小不同的正方形相似.( 命题)
(2)如图①,在四边形ABCD 和四边形 中,
求证:四边形ABCD 与四边形. 相似;
(3)如图②,四边形ABCD中,AB∥CD,AC与BD 相交于点O,过点O作. 分别交AD,BC于点E,F.记四边形ABFE的面积为S ,四边形EFCD的面积为( ,若四边形ABFE 与四边形EFCD 相似,求 的值.
22.(10分)如图,在Rt△ABC中,M是斜边AB 的中点,以CM为直径作圆O交AC 于点 N,延长 MN 至点D,使 ND=MN,连结AD,CD,CD交圆O于点E,连结 NE.
(1)判断四边形 AMCD的形状,并说明理由;
(2)求证:ND=NE;
(3)若DE=2,EC=3,求 BC的长.
23.(10分)如图1,排球场长为18m,宽为9m,网高为2.24m.队员站在底线O点处发球,球从点O的正上方1.9m的C 点发出,运动路线是抛物线的一部分,当球运动到最高点 A 时,高度为 2.88m.即BA=2.88m.这时水平距离OB=7m,以直线OB为x轴,直线OC为y轴,建立平面直角坐标系,如图2.(1)若球向正前方运动(即x轴垂直于底线),求球运动的高度y(m)与水平距离x(m)之间的函数关系式(不必写出x取值范围).并判断这次发球能否过网 是否出界 说明理由;
(2)若球过网后的落点是对方场地①号位内的点 P(如图1,点P距底线1m,边线0.5m),问发球点O在底线上的哪个位置 (参考数据 取1.4)
24.(12分)如图,在△ABC中,∠ACB=90°,将△ABC沿直线AB 翻折得到△ABD,连结CD交AB 于点M. E是线段CM上的点,连结 BE. F 是△BDE的外接圆与AD 的另一个交点,连结 EF,BF.
(1)求证: 是直角三角形;
(2)求证:
(3)当AB=6,BC=m时,在线段CM上存在点E,使得EF和AB 互相平分,求m的值.
期末测试卷
D 2. A 3. C 4. D 5. D 6. A 7. A8. C 9. B 10. B 11. 114 12. 0.90 13 14. 8 15. 11 16. (1,0)
17. 解:(1)把 B(1,0)代入 得0=a+4 解得 +1,∴点A的坐标为(2,1),∵抛物线的对称轴为直线x=2,且点C与点B 关于对称轴对称,∴点 C的坐标为(3,0),∴当y>0时,x的取值范围是1
18. 解:作图的依据是:直径所对的圆周角是直角,等边三角形的每个内角为 60°,直角三角形两锐角互余等.如图,连结OD,CD.由作图可知:OD= OC = CD,∴△ODC是等边三角形,
∴∠DCO=60°,∵AC 是⊙O直 径, ∴ ∠ADC = 90°,
19. (1)证明:设正方形的边长为4a,∵E为AD 的中点,∴AE=ED=2a,∵FC=3DF,∴DF=a,FC= 又∠A=∠D=90°,∴△ABE∽△DEF.
(2)解:∵AD=4,∴DE=2,∵AD∥BC,∴△EDF∽△GCF,∴ ∴△BEG的面积
20.(1)
卡1 卡2 1 2 3 4
1 3 4 5
2 3 5 6
3 4 5 7
4 5 6 7
由表知,一共有12种等可能情况,其中抽取的两数之和大于4的情况有8种, 即抽取的2张卡片所标数字之和大于4的概率为
21. (1)假 假 真 (2)证明:连结 BD,B D .∵ 且 ∴四边形ABCD与四边形. 相似.
(3)解:∵四边形 ABFE 与四边形 EFCD 相似,
22. (1)解:四边形 AMCD 是菱形.理由如下:∵M是 中AB 边的中点, 为⊙O的直径, =CN,∵ND=MN,∴四边形AMCD是菱形.
(2)证明:∵四边形CENM为⊙O的内接四边形,∴∠CEN+∠CMN=180°,∵∠CEN+∠DEN=180°,∴∠CMN=∠DEN,∵四边形 AMCD是菱形,∴CD=CM,∴∠CDM=∠CMN,∴∠DEN=∠CDM,∴ ND= NE. (3)解:∵∠CMN =∠DEN,∠MDC=∠EDN,∴△MDC∽△EDN, 设 DN=x,则MD=2x,由此得 解得: 或x= (不合题意,舍去),∴ 易知 MN 为△ABC的中位线,∴BC=
23. 解:(1)设抛物线的表达式为: 把(0,1.9)代入,得 解得 .抛物线的表达式为 2.88.当x=9时,
2.24,当x=18时, >0,故这次发球过网,但是出界了.
(2)分别过点 P,Q作底线、边线的平行线 PQ,OQ 交 于 点 Q, 则 在 Rt△OPQ中,OQ=18-1=17,当y=0时, 解得x=19或x=-5(其中. -5舍去).∴OP=19,而 OQ=17,故 8.4.∵9-8.4-0.5=0.1,∴发球点O右底线⊥l距右边线0.1m处.
24. (1)证明:∵△ABD是由△ABC 翻折得到的,∴∠ADB = ∠ACB = 90°. ∵∠EF., ∠EDB,∠EBF=∠EDF,∴∠EFB+∠EBF=∠EDB+∠EDF=∠ADB=90°,
∴∠BEF=90°,∴△BEF是直角三角形.
(2)证明:由翻折得AC=AD,∵BC=BD,
∴∠BDC=∠BCD,
∵∠EFB=∠EDB,
∴∠EFB=∠BCD.
∵AC=AD,BC=BD,∴AB⊥CD,∴∠AMC=90°.∵∠BCD+∠ACD=∠ACD+∠CAB=90°,
∴∠BCD=∠CAB,∴∠BFE=∠CAB,
∵∠ACB=∠FEB=90°,∴△BEF∽△BCA.
(3)解:设EF 交 AB 于点J.连结AE,如图.∵EF 与AB 互相平分,∴四边形 AFBE是平行四边形,∴BE∥AF,∴∠EFA=∠FEB=90°,即EF⊥AD.
∵BD⊥AD,∴EF∥BD,∵AJ=JB,∴AF=DF,∴FJ BD=π/ ∴EF=m,∵△ABC∽△CBM,∴BC: MB=AB: BC,∴BM= ,∵△BEJ∽△BME,∴BE 即 解得 (负根 已经舍弃).
同课章节目录
