上海市金山区2015学年第一学期期末考试高三数学试卷
文档属性
| 名称 | 上海市金山区2015学年第一学期期末考试高三数学试卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 102.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-11 00:00:00 | ||
图片预览


文档简介
金山区2015学年第一学期期末考试
高三数学试卷
(满分:150分,完卷时间:120分钟)
(答题请写在答题纸上)
一、填空题(本大题满分56分)本大题共有14题,考生应在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分.
1.= .
2.已知全集U=R,集合M={x | x2–4x–5<0},N={x | x≥1},则M∩(UN) = .
3.若复数满足(i为虚数单位),则= .
4.若直线l1:6x+my–1=0与直线l2:2x-y+1=0平行,则m= .
5. 若线性方程组的增广矩阵为,解为,则c1–c2= .
6.方程4x– 62x +8=0的解是 .
7.函数y=secx sinx的最小正周期T= .
8.二项式展开式中系数的值是 .
9.以椭圆的中心为顶点,且以该椭圆的右焦点为焦点的抛物线方程是 .
10.在报名的5名男生和3名女生中,选取 ( http: / / www.21cnjy.com )5人参加数学竞赛,要求男、女生都有,则不同的选取方式的种数为 .(结果用数值表示)
11.方程cos2x+sinx=1在(0,)上的解集是 .
12.行列式(a、b、c、d{–1,1,2})所有可能的值中,最小值为 .
13.已知点P、Q分别为函数 (x≥0)和图像上的点,则点P和Q两点距离的最小值为 .
14.某种游戏中,用黑、黄两个点表示黑、黄 ( http: / / www.21cnjy.com )两个“电子狗”,它们从棱长为1的正方体ABCD–A1B1C1D1的顶点A出发沿棱向前爬行,每爬完一条棱称为“爬完一段”.黑“电子狗”爬行的路线是AA1→A1D1→…,黄“电子狗”爬行的路线是AB→BB1→…,它们都遵循如下规则:所爬行的第i+2段与第i段所在直线必须是异面直线(其中i是正整数).设黑“电子狗”爬完2015段、黄“电子狗”爬完2014段后各自停止在正方体的某个顶点处,这时黑、黄“电子狗”间的距离是 .
二、选择题(本大题满分20分)本大题共有4 ( http: / / www.21cnjy.com )题,每题有且只有一个正确答案,考生应在答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分.
15.“直线l1、l2互相垂直”是“直线l1、l2的斜率之积等于–1”的( ).
(A) 充分不必要条件 (B) 必要不充分条件
(C) 充要条件 (D) 既非充分也非必要条件
16.若m、n是任意实数,且m>n,则( ).
(A) m2>n2 (B)
(C) lg(m–n)>0 (D)
17.已知,是单位向量,,且向量满足=1,则||的取值范围是( ).
(A) (B)
(C) (D)
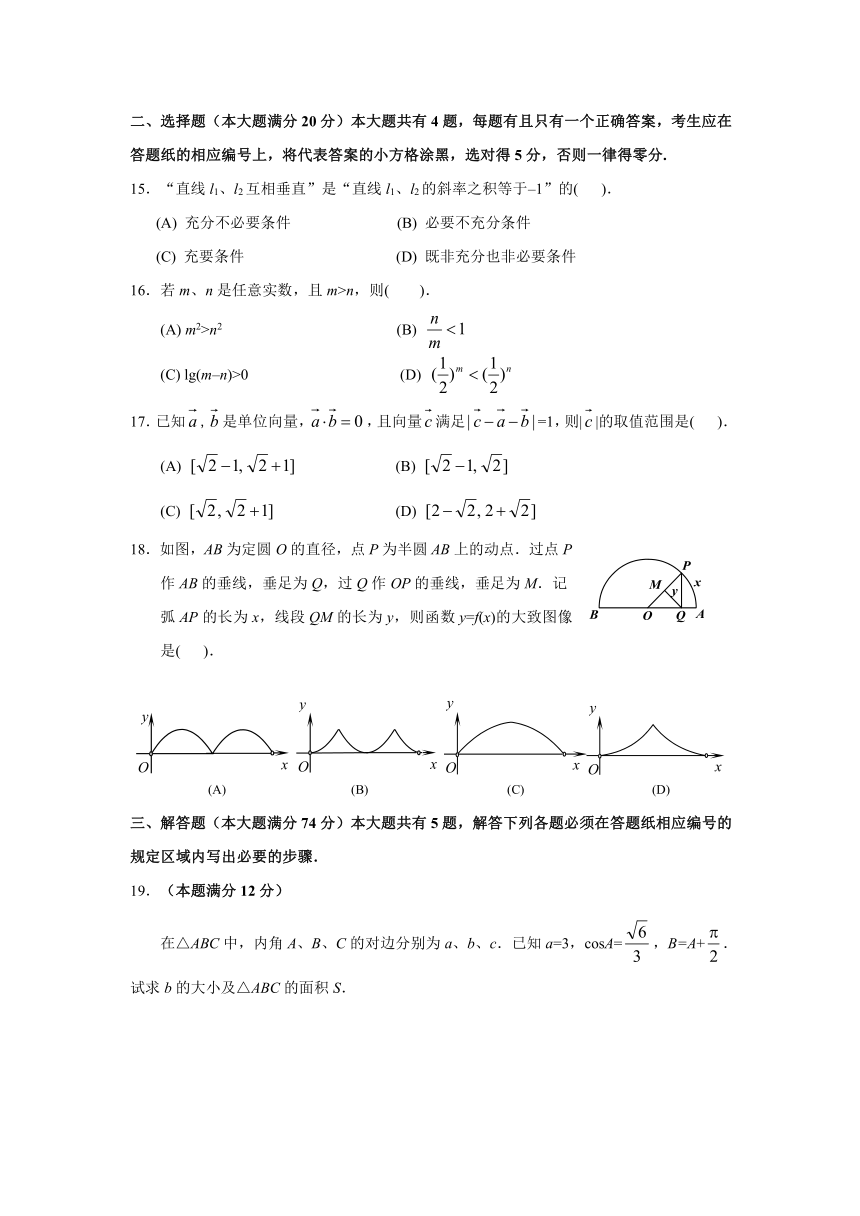
18.如图,AB为定圆O的直径,点P为半圆AB上的动点.过点P
作AB的垂线,垂足为Q,过Q作OP的垂线,垂足为M.记
弧AP的长为x,线段QM的长为y,则函数y=f(x)的大致图像是( ).
三、解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.
19.(本题满分12分)
在△ABC中,内角A、B、C的对边分别为a、b、c.已知a=3,cosA=,B=A+.
试求b的大小及△ABC的面积S.
20.(本题满分14分,第(1)小题6分,第(2)小题8分)
在直三棱柱中,,,且异面直线与所成的角等于,设.
(1) 求的值;
(2) 求三棱锥的体积.
21.(本题满分14分) 本题共有2个小题,第1小题满分7分,第2小题满分7分.
在平面直角坐标系中,已知椭圆,设点 是椭圆上一点,从原点向圆作两条切线,切点分别为.
(1) 若直线互相垂直,且点在第一象限内,求点的坐标;
(2) 若直线的斜率都存在,并记为,求证:.
22.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
已知函数.
(1) 当m=2时,证明f(x)在(–∞,0)上是单调递减函数;
(2) 若对任意xR,不等式f(2x) > 0恒成立,求m的取值范围;
(3) 讨论函数y=f(x)的零点个数.
23.(本小题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知各项均为正数的数列{an}的前n项和Sn满足S1>1,且(nN*).
(1) 求{an}的通项公式;
(2) 设数列满足,Tn为数列{bn}的前n项和,求Tn;
(3) 设,问是否存在正整数,使得当任意正整数n > N时恒有Cn>2015成立?若存在,请求出正整数的取值范围;若不存在,请说明理由.
金山区2015学年第一学期期末考试高三数学试卷
评分参考意见
一、填空题(本大题满分56分)本大题共有14题,考生应在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分.
1.; 2.{x| –1< x <1}; 3. ; 4.–3; 5. –1;
6. x=1或x=2; 7.; 8.–6; 9.y2=12x; 10.55
11.; 12. –6; 13.; 14..
二、选择题(本大题满分20 ( http: / / www.21cnjy.com )分)本大题共有4题,每题有且只有一个正确答案,考生应在答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分.
15.B; 16.D; 17.A; 18.A
三、解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.
19.解:因为cosA=,所以sinA=,………………………………………………1分
又B=A+,所以sinB=sin(A+)=cosA=,……………………………………………2分
又因为,………………………………………………………………………4分
所以b==,……………………………………………………………………6分
cosB=cos(A+)= –sinA= –………………………………………………………………8分
sinC=sin(A+B)=sinAcosB+cosAsinB=,…………………………………………………10分
所以△ABC的面积S==. ……………………………………………12分
或解:因为a2=b2+c2–2bccosA(2分)
即:c2–4c+9=0,解之得:c=3(舍去),c=,(2分)
△ABC的面积S==.(2分)
20.解(1)∵BC∥B1C1,∴∠A1BC就是异面直线A1B与B1C1所成的角,
即∠A1BC =60,…………………………………………………………………………2分
又AA1⊥平面ABC,AB=AC,则A1B=A1C,∴△A1BC为等边三角形,…………4分
由,,
∴;……………………………………………6分
(2)连接B1C,则三棱锥B1–A1BC的体积等于三棱锥C–A1B1B的体积,
即:,………………………………………………………………9分
△的面积,……………………………………………………………11分
又平面,
所以,所以.………………………………14分
21.解:(1)由题意得:圆的半径为,因为直线互相垂直,且与圆相切,所以四边形OPRQ为正方形,故,即① ………………3分
又在椭圆C上,所以②…………………………………5分
由①②及在第一象限,解得,…………………………………………7分
(2)证明:因为直线OP:y=k1 x,OQ:y=k2x均与圆R相切,……………………8分
所以,化简得
同理有………………………………………………10分
所以k1、k2是方程的两个不相等的实数根,
所以,………………………………………………………………………11分
又因为在椭圆C上,所以,
即,所以,即2k1k2+1=0.………………………14分
22.解:(1) 当m=2,且x<0时,,………………………………1分
证明:设x1又x10,x2x1>0,,所以
所以f(x1)–f(x2)>0,即f(x1) >f(x2),
故当m=2时,在(–∞,0)上单调递减的. …………………………4分
(2)由f(2x)>0得,
变形为,即,
当即x=–1时, ,所以.…………………………10分
(3)由f(x)=0,可得x|x|–x+m=0 (x≠0),变为m=–x|x|+x (x≠0),
令,, 作y=g(x)的图像及直线y=m,由图像可得:
当或时,y=f(x)有1个零点.
当或m=0或时,y=f(x)有2个零点;
当或时,y=f(x)有3个零点.………………………………16分
23.解:(1)时,,且,解得
时,,两式相减得:
即,,
,为等差数列,. ……………………………4分
(2),.
当为偶数时,Tn=(b1+b3+…+bn–1)+(b2+b4+…+bn) ,
当为奇数时,Tn=(b1+b3+…+bn)+(b2+b4+…+bn–1)
………………………………10分
(3),
当n为奇数时,,
∴Cn+2因此不存在满足条件的正整数N.……………………………………………………18分
(A))
x
y
O
(B)
x
y
O
(C)
x
y
O
(D)
x
y
O
A
B
C
A1
B1
C1
高三数学试卷
(满分:150分,完卷时间:120分钟)
(答题请写在答题纸上)
一、填空题(本大题满分56分)本大题共有14题,考生应在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分.
1.= .
2.已知全集U=R,集合M={x | x2–4x–5<0},N={x | x≥1},则M∩(UN) = .
3.若复数满足(i为虚数单位),则= .
4.若直线l1:6x+my–1=0与直线l2:2x-y+1=0平行,则m= .
5. 若线性方程组的增广矩阵为,解为,则c1–c2= .
6.方程4x– 62x +8=0的解是 .
7.函数y=secx sinx的最小正周期T= .
8.二项式展开式中系数的值是 .
9.以椭圆的中心为顶点,且以该椭圆的右焦点为焦点的抛物线方程是 .
10.在报名的5名男生和3名女生中,选取 ( http: / / www.21cnjy.com )5人参加数学竞赛,要求男、女生都有,则不同的选取方式的种数为 .(结果用数值表示)
11.方程cos2x+sinx=1在(0,)上的解集是 .
12.行列式(a、b、c、d{–1,1,2})所有可能的值中,最小值为 .
13.已知点P、Q分别为函数 (x≥0)和图像上的点,则点P和Q两点距离的最小值为 .
14.某种游戏中,用黑、黄两个点表示黑、黄 ( http: / / www.21cnjy.com )两个“电子狗”,它们从棱长为1的正方体ABCD–A1B1C1D1的顶点A出发沿棱向前爬行,每爬完一条棱称为“爬完一段”.黑“电子狗”爬行的路线是AA1→A1D1→…,黄“电子狗”爬行的路线是AB→BB1→…,它们都遵循如下规则:所爬行的第i+2段与第i段所在直线必须是异面直线(其中i是正整数).设黑“电子狗”爬完2015段、黄“电子狗”爬完2014段后各自停止在正方体的某个顶点处,这时黑、黄“电子狗”间的距离是 .
二、选择题(本大题满分20分)本大题共有4 ( http: / / www.21cnjy.com )题,每题有且只有一个正确答案,考生应在答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分.
15.“直线l1、l2互相垂直”是“直线l1、l2的斜率之积等于–1”的( ).
(A) 充分不必要条件 (B) 必要不充分条件
(C) 充要条件 (D) 既非充分也非必要条件
16.若m、n是任意实数,且m>n,则( ).
(A) m2>n2 (B)
(C) lg(m–n)>0 (D)
17.已知,是单位向量,,且向量满足=1,则||的取值范围是( ).
(A) (B)
(C) (D)
18.如图,AB为定圆O的直径,点P为半圆AB上的动点.过点P
作AB的垂线,垂足为Q,过Q作OP的垂线,垂足为M.记
弧AP的长为x,线段QM的长为y,则函数y=f(x)的大致图像是( ).
三、解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.
19.(本题满分12分)
在△ABC中,内角A、B、C的对边分别为a、b、c.已知a=3,cosA=,B=A+.
试求b的大小及△ABC的面积S.
20.(本题满分14分,第(1)小题6分,第(2)小题8分)
在直三棱柱中,,,且异面直线与所成的角等于,设.
(1) 求的值;
(2) 求三棱锥的体积.
21.(本题满分14分) 本题共有2个小题,第1小题满分7分,第2小题满分7分.
在平面直角坐标系中,已知椭圆,设点 是椭圆上一点,从原点向圆作两条切线,切点分别为.
(1) 若直线互相垂直,且点在第一象限内,求点的坐标;
(2) 若直线的斜率都存在,并记为,求证:.
22.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
已知函数.
(1) 当m=2时,证明f(x)在(–∞,0)上是单调递减函数;
(2) 若对任意xR,不等式f(2x) > 0恒成立,求m的取值范围;
(3) 讨论函数y=f(x)的零点个数.
23.(本小题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知各项均为正数的数列{an}的前n项和Sn满足S1>1,且(nN*).
(1) 求{an}的通项公式;
(2) 设数列满足,Tn为数列{bn}的前n项和,求Tn;
(3) 设,问是否存在正整数,使得当任意正整数n > N时恒有Cn>2015成立?若存在,请求出正整数的取值范围;若不存在,请说明理由.
金山区2015学年第一学期期末考试高三数学试卷
评分参考意见
一、填空题(本大题满分56分)本大题共有14题,考生应在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分.
1.; 2.{x| –1< x <1}; 3. ; 4.–3; 5. –1;
6. x=1或x=2; 7.; 8.–6; 9.y2=12x; 10.55
11.; 12. –6; 13.; 14..
二、选择题(本大题满分20 ( http: / / www.21cnjy.com )分)本大题共有4题,每题有且只有一个正确答案,考生应在答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分.
15.B; 16.D; 17.A; 18.A
三、解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.
19.解:因为cosA=,所以sinA=,………………………………………………1分
又B=A+,所以sinB=sin(A+)=cosA=,……………………………………………2分
又因为,………………………………………………………………………4分
所以b==,……………………………………………………………………6分
cosB=cos(A+)= –sinA= –………………………………………………………………8分
sinC=sin(A+B)=sinAcosB+cosAsinB=,…………………………………………………10分
所以△ABC的面积S==. ……………………………………………12分
或解:因为a2=b2+c2–2bccosA(2分)
即:c2–4c+9=0,解之得:c=3(舍去),c=,(2分)
△ABC的面积S==.(2分)
20.解(1)∵BC∥B1C1,∴∠A1BC就是异面直线A1B与B1C1所成的角,
即∠A1BC =60,…………………………………………………………………………2分
又AA1⊥平面ABC,AB=AC,则A1B=A1C,∴△A1BC为等边三角形,…………4分
由,,
∴;……………………………………………6分
(2)连接B1C,则三棱锥B1–A1BC的体积等于三棱锥C–A1B1B的体积,
即:,………………………………………………………………9分
△的面积,……………………………………………………………11分
又平面,
所以,所以.………………………………14分
21.解:(1)由题意得:圆的半径为,因为直线互相垂直,且与圆相切,所以四边形OPRQ为正方形,故,即① ………………3分
又在椭圆C上,所以②…………………………………5分
由①②及在第一象限,解得,…………………………………………7分
(2)证明:因为直线OP:y=k1 x,OQ:y=k2x均与圆R相切,……………………8分
所以,化简得
同理有………………………………………………10分
所以k1、k2是方程的两个不相等的实数根,
所以,………………………………………………………………………11分
又因为在椭圆C上,所以,
即,所以,即2k1k2+1=0.………………………14分
22.解:(1) 当m=2,且x<0时,,………………………………1分
证明:设x1
所以f(x1)–f(x2)>0,即f(x1) >f(x2),
故当m=2时,在(–∞,0)上单调递减的. …………………………4分
(2)由f(2x)>0得,
变形为,即,
当即x=–1时, ,所以.…………………………10分
(3)由f(x)=0,可得x|x|–x+m=0 (x≠0),变为m=–x|x|+x (x≠0),
令,, 作y=g(x)的图像及直线y=m,由图像可得:
当或时,y=f(x)有1个零点.
当或m=0或时,y=f(x)有2个零点;
当或时,y=f(x)有3个零点.………………………………16分
23.解:(1)时,,且,解得
时,,两式相减得:
即,,
,为等差数列,. ……………………………4分
(2),.
当为偶数时,Tn=(b1+b3+…+bn–1)+(b2+b4+…+bn) ,
当为奇数时,Tn=(b1+b3+…+bn)+(b2+b4+…+bn–1)
………………………………10分
(3),
当n为奇数时,,
∴Cn+2
(A))
x
y
O
(B)
x
y
O
(C)
x
y
O
(D)
x
y
O
A
B
C
A1
B1
C1
同课章节目录
