第二章《轴对称》综合测试卷(含答案)
图片预览




文档简介
中小学教育资源及组卷应用平台
第二章综合测试卷
时间: 45分钟 满分: 100分 得 分:__________
一、选择题(每题3分,共30分)
1.书法是我国特有的优秀传统文化,其中篆书具有象形特征,充满美感.下列“福”字的四种篆书图案中,可以看作轴对称图形的是 ( )
2.如图,
上.正确的有 ( )
A.4个 B.3个 C.2个 D.1个
第2题图 第3题图
3.某城市几条道路的位置关系如图所示,道路AB∥CD,道路AB与AE 的夹角,城市规划部门想新修一条道路CE,要求CF=EF,则的度数为( )
A.23° B.25° C.27°
4.如图,某研究性学习小组为测量学校 A 与河对岸工厂B 之间的距离,在学校附近选一点 C,利用测量仪器测得.据此,可求得学校与工厂之间的距离 AB 等于 ( )
5.如图,直线a∥b,等边三角形 ABC 的顶点C 在直线b上,∠2=40°,则∠1的度数为 ( )
A.80° B.70° C.60° D.50°
6.如图所示,在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点 E,BC=5,DE=2,则△BCE的面积等于 ( )
A.10 B.7 C.5 D.4
第6题图 第7题图
7.如图所示,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为 ( )
A.44° B.66° C.88° D.92°
8.如图所示,在 Rt△ABC 中,CM平分∠ACB 交AB 于点M,过点 M 作 MN∥BC 交 AC 于点 N,且 MN 平分∠AMC,若AN=1,则 AC的长为 ( )
A.2 B.3 C.4 D.5
9.在和中,,已知 ( )
10.如图,过边长为 4 的等边三角形的边 AB 上一点 P,作PE⊥AC于点E,Q为BC 延长线上一点,当 PA=CQ 时,连接 PQ交边AC 于点 D,则 DE 的长为 ( )
A.2 B.3 C.4
二、填空题(每题4 分,共24分)
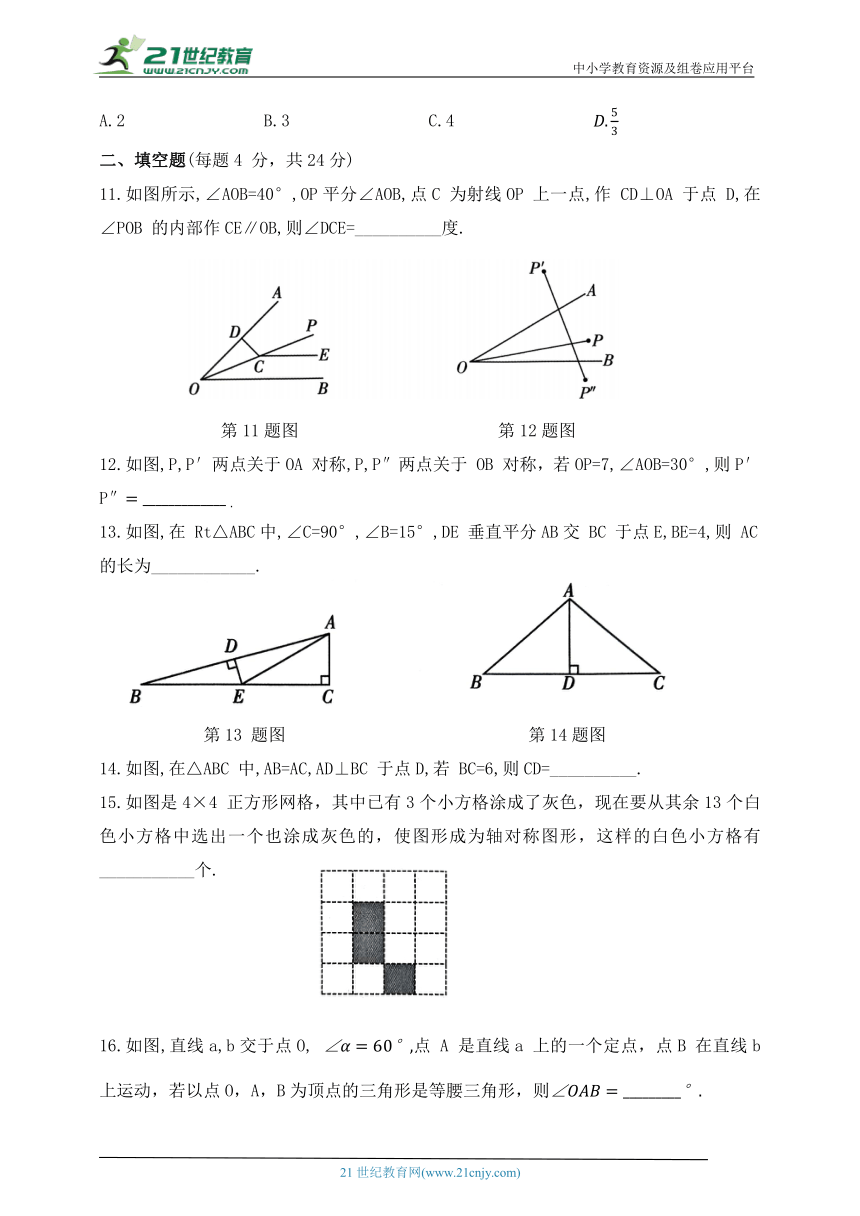
11.如图所示,∠AOB=40°,OP平分∠AOB,点C 为射线OP 上一点,作 CD⊥OA 于点 D,在∠POB 的内部作CE∥OB,则∠DCE=__________度.
第11题图 第12题图
12.如图,P,P′两点关于OA 对称,P,P″两点关于 OB 对称,若OP=7,∠AOB=30°,则P′P″
13.如图,在 Rt△ABC中,∠C=90°,∠B=15°,DE 垂直平分AB交 BC 于点E,BE=4,则 AC的长为____________.
第13 题图 第14题图
14.如图,在△ABC 中,AB=AC,AD⊥BC 于点D,若 BC=6,则CD=__________.
15.如图是4×4 正方形网格,其中已有3个小方格涂成了灰色,现在要从其余13个白色小方格中选出一个也涂成灰色的,使图形成为轴对称图形,这样的白色小方格有___________个.
16.如图,直线a,b交于点O, 点 A 是直线a 上的一个定点,点B 在直线b上运动,若以点O,A,B为顶点的三角形是等腰三角形,则
三、解答题(共46分)
17.(8分)如图,在边长为单位1的正方形网格中有
(1)在图中画出△ABC 关于直线MN 成轴对称的图形
(2)求△ABC的面积;
(3)在直线 MN 上有一点 P 使得PA+PB的值最小,请在图中标出点 P 的位置.
18.(8分)如图,在 中,
(1)通过观察尺规作图的痕迹,可以发现直线 DF 是线段AB的_________,射线 AE 是 的____________;
(2)在(1)所作的图中,求 的度数.
19.(10 分)如图,在中,的平分线交AC于点D,过点D作∥交AB 于点 E.
(1)求证:
(2)若 求 的度数.
20.(10分)如图,一条船上午8时从海岛A出发,以15海里/时的速度向正北方向航行,上午10时到达海岛 B 处,分别从 A,B处望灯塔C,测得
(1)求海岛 B 到灯塔C 的距离:
(2)若这条船到达海岛 B 处后,继续向正北方向航行,问还要经过多长时间,小船与灯塔C的距离最短
21.(10分)如图,点 O 是等边 内一点,D是 外的一点, 连接OD.
(1)求证: 是等边三角形;
(2)当 时,试判断 的形状,并说明理由;
(3)探究:当α为多少度时, 是等腰三角形.
参考答案
1. C 2. B 3. B 4. D 5. A 6. C 7. D 8. B
9. C 解析:当. 时, (SSS),所以
当 时,
因为 所以
所以 所以 或
10. A 11.130 12.7 13.2 14.3 15.4
16.60或30 解析:如图1,当点 B在OA上方时,
根据题意得,∠AOB=60°,
因为△OAB是等腰三角形,所以△OAB是等边三角形,所以∠OAB=60°;
如图2,当点 B在OA 下方时,OA=OB,
所以∠OBA=∠OAB,
因为∠α=60°,所以∠BOA=120°,
所以∠OBA+∠OAB=180°-∠BOA=60°,所以∠OAB=30°.
17.解:(1)如图, 即为所求作;
(3)如图,点P 即为所求作.
18.解:(1)通过观察尺规作图的痕迹,可以发现直线 DF 是线段AB 的垂直平分线,射线 AE是∠DAC的角平分线.
故答案为:垂直平分线,角平分线;
(2)因为 DF垂直平分线段AB,所以 DA=DB,
所以∠BAD=∠B=40°,
因为∠B=40°,∠C=50°,所以∠BAC=90°,所以∠CAD=50°,
因为 AE 平分∠CAD,所以
19.解:(1)证明:在△ABC 中,∠ABC 的平分线交AC 于点 D,
所以∠ABD=∠CBD,
因为 DE∥BC,所以∠EDB=∠CBD,所以∠EBD=∠EDB,所以 BE=DE;
(2)因为∠A=80°,∠C=40°,所以∠ABC=60°,
因为∠ABC的平分线交AC 于点 D,
所以
因为 DE∥BC,所以∠EDB=∠CBD=30°,所以∠BDE=30°.
20.解:(1)由题意,得AB=15×2=30(海里),
因为∠NBC=60°,∠NAC=30°,
所以 ∠ACB =180°-∠CBA-∠NAC =∠NBC-∠NAC=30°,
所以∠ACB=∠NAC,所以AB=BC=30(海里),
所以从海岛 B到灯塔C 的距离为 30 海里;
(2)如图,过点 C 作CP⊥AB于点 P.
所以根据垂线段最短,线段 CP 的长为小船与灯塔C 的最短距离,∠BPC=90°.
又因为∠NBC=60°,所以∠PCB=180°-∠BPC-∠CBP=30°.
在 Rt△CBP中,∠BCP=30°,所以 (海里),15÷15=1(小时).
所以还要经过1小时,小船与灯塔C的距离最短.
21.解:证明:(1)因为△BOC≌△ADC,所以OC=DC,
因为∠OCD=60°,所以△OCD是等边三角形;
(2)△AOD 是直角三角形.
理由:
因为△OCD是等边三角形,所以∠ODC=60°,
因为△BOC≌△ADC,α=150°,所以∠ADC=∠BOC=α=150°,
所以∠ADO=∠ADC-∠ODC=150°-60°=90°,
所以△AOD 是直角三角形;
(3)因为△OCD是等边三角形,所以∠COD=∠ODC=60°,
因为∠AOB=110°,∠ADC=∠BOC=α,
所以∠AOD =360°-∠AOB-∠BOC -∠COD=360°-110°-α-60°= 190°-α,
∠ADO=∠ADC-∠ODC=α-60°,
所以∠OAD=180°-∠AOD-∠ADO=180°-(190°-α)-(α-60°)=50°.
①当∠AOD=∠ADO时,190°-α=α-60°,所以α=125°;
②当∠AOD=∠OAD时,190°-α=50°,所以α=140°;
③当∠ADO=∠OAD 时,α-60°=50°,所以α=110°.
综上所述,当α=110°或 125°或 140°时,△AOD 是等腰三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章综合测试卷
时间: 45分钟 满分: 100分 得 分:__________
一、选择题(每题3分,共30分)
1.书法是我国特有的优秀传统文化,其中篆书具有象形特征,充满美感.下列“福”字的四种篆书图案中,可以看作轴对称图形的是 ( )
2.如图,
上.正确的有 ( )
A.4个 B.3个 C.2个 D.1个
第2题图 第3题图
3.某城市几条道路的位置关系如图所示,道路AB∥CD,道路AB与AE 的夹角,城市规划部门想新修一条道路CE,要求CF=EF,则的度数为( )
A.23° B.25° C.27°
4.如图,某研究性学习小组为测量学校 A 与河对岸工厂B 之间的距离,在学校附近选一点 C,利用测量仪器测得.据此,可求得学校与工厂之间的距离 AB 等于 ( )
5.如图,直线a∥b,等边三角形 ABC 的顶点C 在直线b上,∠2=40°,则∠1的度数为 ( )
A.80° B.70° C.60° D.50°
6.如图所示,在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点 E,BC=5,DE=2,则△BCE的面积等于 ( )
A.10 B.7 C.5 D.4
第6题图 第7题图
7.如图所示,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为 ( )
A.44° B.66° C.88° D.92°
8.如图所示,在 Rt△ABC 中,CM平分∠ACB 交AB 于点M,过点 M 作 MN∥BC 交 AC 于点 N,且 MN 平分∠AMC,若AN=1,则 AC的长为 ( )
A.2 B.3 C.4 D.5
9.在和中,,已知 ( )
10.如图,过边长为 4 的等边三角形的边 AB 上一点 P,作PE⊥AC于点E,Q为BC 延长线上一点,当 PA=CQ 时,连接 PQ交边AC 于点 D,则 DE 的长为 ( )
A.2 B.3 C.4
二、填空题(每题4 分,共24分)
11.如图所示,∠AOB=40°,OP平分∠AOB,点C 为射线OP 上一点,作 CD⊥OA 于点 D,在∠POB 的内部作CE∥OB,则∠DCE=__________度.
第11题图 第12题图
12.如图,P,P′两点关于OA 对称,P,P″两点关于 OB 对称,若OP=7,∠AOB=30°,则P′P″
13.如图,在 Rt△ABC中,∠C=90°,∠B=15°,DE 垂直平分AB交 BC 于点E,BE=4,则 AC的长为____________.
第13 题图 第14题图
14.如图,在△ABC 中,AB=AC,AD⊥BC 于点D,若 BC=6,则CD=__________.
15.如图是4×4 正方形网格,其中已有3个小方格涂成了灰色,现在要从其余13个白色小方格中选出一个也涂成灰色的,使图形成为轴对称图形,这样的白色小方格有___________个.
16.如图,直线a,b交于点O, 点 A 是直线a 上的一个定点,点B 在直线b上运动,若以点O,A,B为顶点的三角形是等腰三角形,则
三、解答题(共46分)
17.(8分)如图,在边长为单位1的正方形网格中有
(1)在图中画出△ABC 关于直线MN 成轴对称的图形
(2)求△ABC的面积;
(3)在直线 MN 上有一点 P 使得PA+PB的值最小,请在图中标出点 P 的位置.
18.(8分)如图,在 中,
(1)通过观察尺规作图的痕迹,可以发现直线 DF 是线段AB的_________,射线 AE 是 的____________;
(2)在(1)所作的图中,求 的度数.
19.(10 分)如图,在中,的平分线交AC于点D,过点D作∥交AB 于点 E.
(1)求证:
(2)若 求 的度数.
20.(10分)如图,一条船上午8时从海岛A出发,以15海里/时的速度向正北方向航行,上午10时到达海岛 B 处,分别从 A,B处望灯塔C,测得
(1)求海岛 B 到灯塔C 的距离:
(2)若这条船到达海岛 B 处后,继续向正北方向航行,问还要经过多长时间,小船与灯塔C的距离最短
21.(10分)如图,点 O 是等边 内一点,D是 外的一点, 连接OD.
(1)求证: 是等边三角形;
(2)当 时,试判断 的形状,并说明理由;
(3)探究:当α为多少度时, 是等腰三角形.
参考答案
1. C 2. B 3. B 4. D 5. A 6. C 7. D 8. B
9. C 解析:当. 时, (SSS),所以
当 时,
因为 所以
所以 所以 或
10. A 11.130 12.7 13.2 14.3 15.4
16.60或30 解析:如图1,当点 B在OA上方时,
根据题意得,∠AOB=60°,
因为△OAB是等腰三角形,所以△OAB是等边三角形,所以∠OAB=60°;
如图2,当点 B在OA 下方时,OA=OB,
所以∠OBA=∠OAB,
因为∠α=60°,所以∠BOA=120°,
所以∠OBA+∠OAB=180°-∠BOA=60°,所以∠OAB=30°.
17.解:(1)如图, 即为所求作;
(3)如图,点P 即为所求作.
18.解:(1)通过观察尺规作图的痕迹,可以发现直线 DF 是线段AB 的垂直平分线,射线 AE是∠DAC的角平分线.
故答案为:垂直平分线,角平分线;
(2)因为 DF垂直平分线段AB,所以 DA=DB,
所以∠BAD=∠B=40°,
因为∠B=40°,∠C=50°,所以∠BAC=90°,所以∠CAD=50°,
因为 AE 平分∠CAD,所以
19.解:(1)证明:在△ABC 中,∠ABC 的平分线交AC 于点 D,
所以∠ABD=∠CBD,
因为 DE∥BC,所以∠EDB=∠CBD,所以∠EBD=∠EDB,所以 BE=DE;
(2)因为∠A=80°,∠C=40°,所以∠ABC=60°,
因为∠ABC的平分线交AC 于点 D,
所以
因为 DE∥BC,所以∠EDB=∠CBD=30°,所以∠BDE=30°.
20.解:(1)由题意,得AB=15×2=30(海里),
因为∠NBC=60°,∠NAC=30°,
所以 ∠ACB =180°-∠CBA-∠NAC =∠NBC-∠NAC=30°,
所以∠ACB=∠NAC,所以AB=BC=30(海里),
所以从海岛 B到灯塔C 的距离为 30 海里;
(2)如图,过点 C 作CP⊥AB于点 P.
所以根据垂线段最短,线段 CP 的长为小船与灯塔C 的最短距离,∠BPC=90°.
又因为∠NBC=60°,所以∠PCB=180°-∠BPC-∠CBP=30°.
在 Rt△CBP中,∠BCP=30°,所以 (海里),15÷15=1(小时).
所以还要经过1小时,小船与灯塔C的距离最短.
21.解:证明:(1)因为△BOC≌△ADC,所以OC=DC,
因为∠OCD=60°,所以△OCD是等边三角形;
(2)△AOD 是直角三角形.
理由:
因为△OCD是等边三角形,所以∠ODC=60°,
因为△BOC≌△ADC,α=150°,所以∠ADC=∠BOC=α=150°,
所以∠ADO=∠ADC-∠ODC=150°-60°=90°,
所以△AOD 是直角三角形;
(3)因为△OCD是等边三角形,所以∠COD=∠ODC=60°,
因为∠AOB=110°,∠ADC=∠BOC=α,
所以∠AOD =360°-∠AOB-∠BOC -∠COD=360°-110°-α-60°= 190°-α,
∠ADO=∠ADC-∠ODC=α-60°,
所以∠OAD=180°-∠AOD-∠ADO=180°-(190°-α)-(α-60°)=50°.
①当∠AOD=∠ADO时,190°-α=α-60°,所以α=125°;
②当∠AOD=∠OAD时,190°-α=50°,所以α=140°;
③当∠ADO=∠OAD 时,α-60°=50°,所以α=110°.
综上所述,当α=110°或 125°或 140°时,△AOD 是等腰三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
