第一章 勾股定理单元质检卷(A卷)(含解析) 2024-2025学年北师大版(2012)八年级上册数学
文档属性
| 名称 | 第一章 勾股定理单元质检卷(A卷)(含解析) 2024-2025学年北师大版(2012)八年级上册数学 |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-15 21:19:07 | ||
图片预览



文档简介
(1)勾股定理—八年级上册数学北师大版(2012)单元质检卷(A卷)
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面、求这根芦苇的长度是多少尺?设芦苇的长度是x尺,根据题意,可列方程为( )
A. B.
C. D.
2.如图,分别以直角三角形的三边为边向外作三个正方形,较大两个正方形的面积分别为169和144,则最小正方形A的边长是( )
A.25 B.1 C.12 D.5
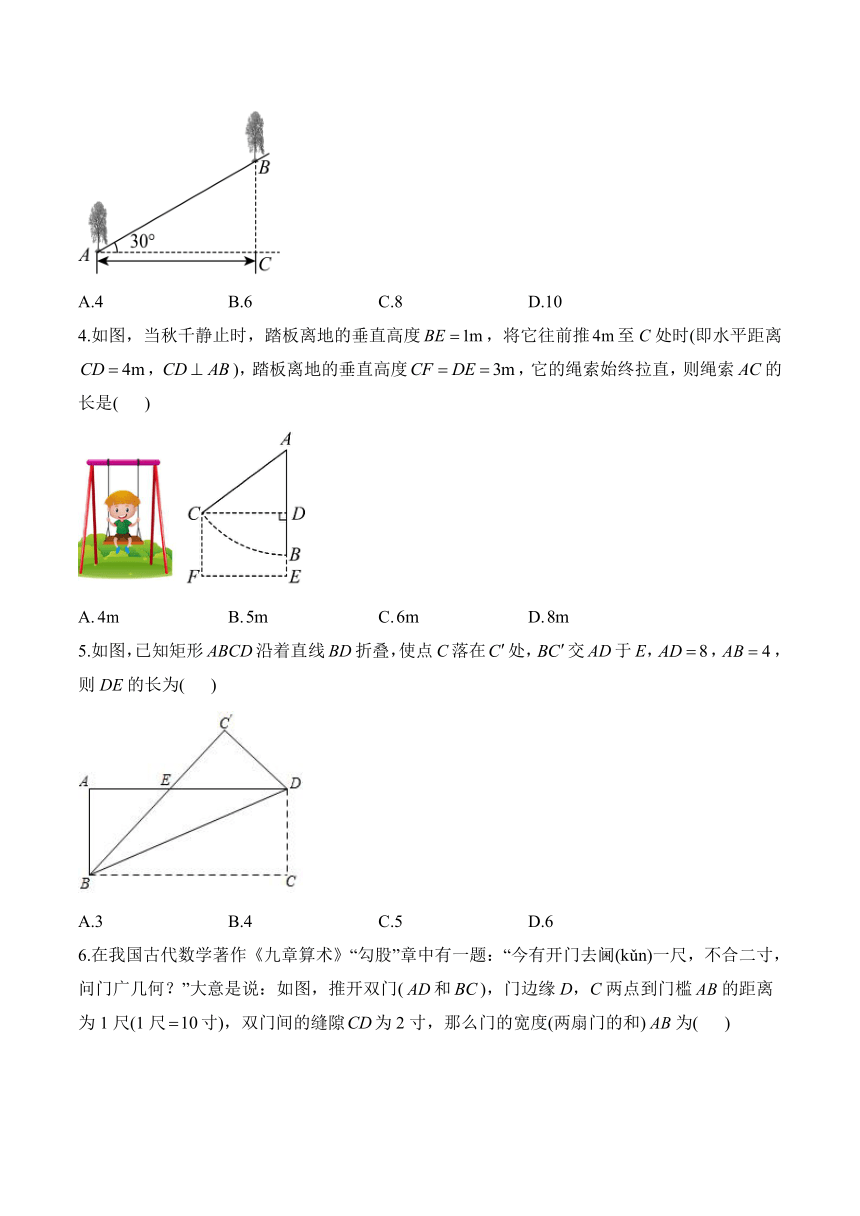
3.如图,在与水平面成角的斜坡上有两棵一样高的柳树,两棵树水平距离,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了( )米.
A.4 B.6 C.8 D.10
4.如图,当秋千静止时,踏板离地的垂直高度,将它往前推至C处时(即水平距离,),踏板离地的垂直高度,它的绳索始终拉直,则绳索的长是( )
A. B. C. D.
5.如图,已知矩形ABCD沿着直线BD折叠,使点C落在处,交AD于E,,,则DE的长为( )
A.3 B.4 C.5 D.6
6.在我国古代数学著作《九章算术》“勾股”章中有一题:“今有开门去阃(kǔn)一尺,不合二寸,问门广几何?”大意是说:如图,推开双门(和),门边缘D,C两点到门槛的距离为1尺(1尺寸),双门间的缝隙为2寸,那么门的宽度(两扇门的和)为( )
A.103寸 B.102寸 C.101寸 D.100寸
7.如图,有四个三角形,各有一边长为6,一边长为8,若第三边分别为6,8,10,12,则面积最大的三角形是( )
A. B.
C. D.
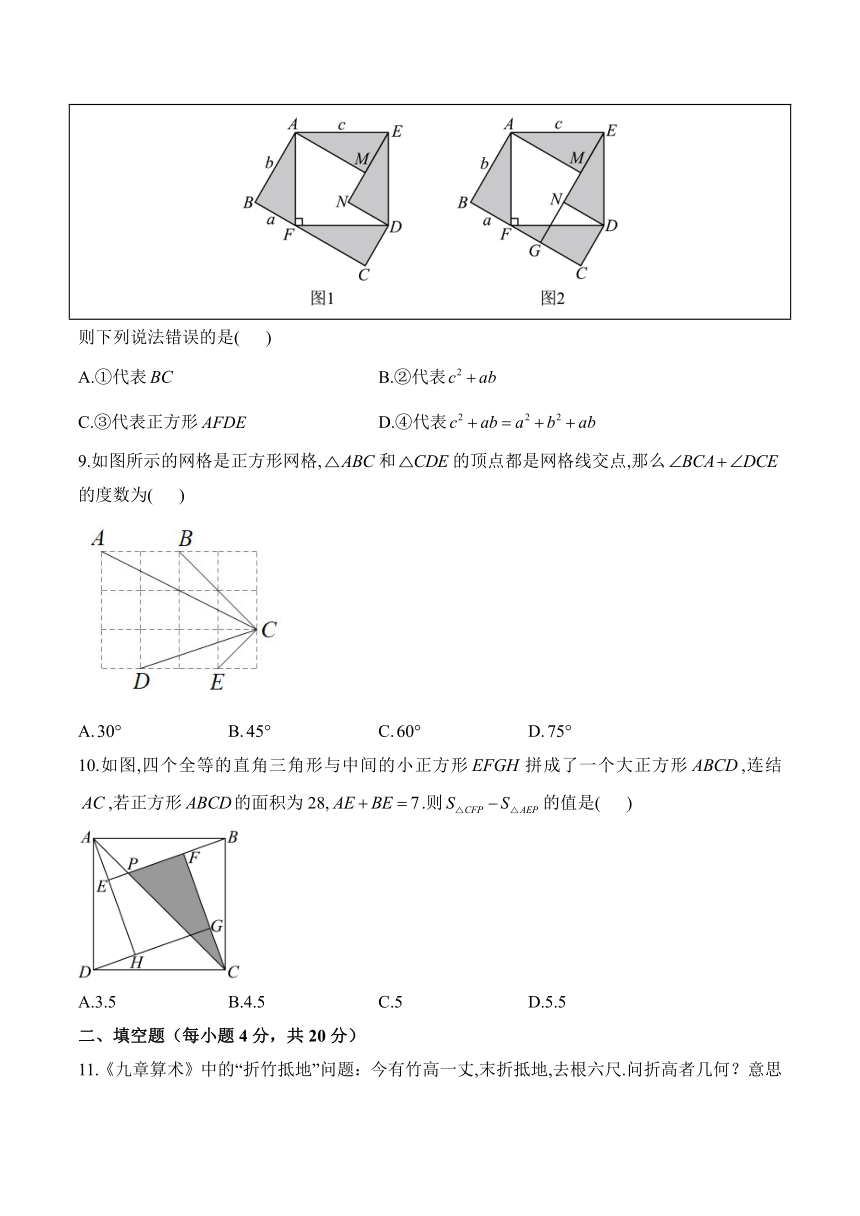
8.《勾股举隅》为梅文鼎研究中国传统勾股算术的著作,其中的主要成就是证明了勾股定理和对勾股算术算法进行了推广.书中的证明方法是将4个三边长分别为,,的全等直角三角形拼成如图1所示的五边形,然后通过添加辅助线,用面积法证明勾股定理.下面是小华给出的相关证明:
如图2,延长交_____①_____于点G. 用两种不同的方法表示五边形的面积S: 方法一:将五边形看成是由正方形与,拼成,则_____②_____. 方法二:将五边形看成是由_____③_____,正方形,,拼成,则. 根据面积相等可以得到_____④_____,即.
则下列说法错误的是( )
A.①代表 B.②代表
C.③代表正方形 D.④代表
9.如图所示的网格是正方形网格,和的顶点都是网格线交点,那么的度数为( )
A. B. C. D.
10.如图,四个全等的直角三角形与中间的小正方形拼成了一个大正方形,连结,若正方形的面积为28,.则的值是( )
A.3.5 B.4.5 C.5 D.5.5
二、填空题(每小题4分,共20分)
11.《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为_______________.
12.我国古代数学名著《算法统宗》有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,5尺人高曾记,仕女家人争蹴.良工高士素好奇,算出索长有几?”此问题可理解为:“如图,有一架秋千,当它静止时,踏板离地距离的长为1尺,将它向前水平推送10尺时,即尺,秋千踏板离地的距离和身高5尺的人一样高,秋千的绳索始终拉得很直,试问绳索有多长?”,设秋千的绳索长为x尺,根据题意可列方程为______.
13.如图,以的两条直角边和斜边为边长分别作正方形,其中正方形、正方形的面积分别为25、144,则阴影部分的面积为______.
14.观察下列几组勾股数:①3、4、5;②5、12、13;③7、24、25;④9、40、41;…根据上面的规律,写出第8组勾股数:______.
15.如图,一架秋千静止时,踏板离地的垂直高度,将它往前推送1.5m(水平距离)时,秋千的踏板离地的垂直高度,秋千的绳索始终拉直,则绳索AD的长是_____m.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)如图,大风把一棵树刮断,已知被刮断前树高,倒下后树干顶部离根部距离,求树折断处与地面的距离(即的长).
17.(8分)阅读下面材料,完成相应的任务.
阿波罗尼奥斯定理
阿波罗尼奥斯(约公元前262-190年),古希腊数学家,与欧几里得、阿基米德合称为古希腊亚历山大前期的三大数学家.阿波罗尼奥斯定理又称中线定理,其内容为三角形两边的平方和等于第三边的一半与第三边上的中线的平方和的两倍.
如图,在中,点D为的中点,根据阿波罗尼奥斯定理,可得.
下面是该定理的部分证明过程:
证明:如图,过点A作于点E.
在中,由勾股定理,得.
同理可得,.
点D为的中点,.
…
任务:
(1)按照上面的思路,将该定理剩余的证明过程补充完整;
(2)请利用阿波罗尼奥斯定理解决下面的问题:如图,已知点P为矩形内任意一点,求证:.
18.(10分)如图,有两只猴子在一棵树高的点B处,它们都要到A处的池塘去喝水,其中一只猴子沿树爬下走到离树处的池塘A处,另一只猴子爬到树顶D后直线跃向池塘的A处,如果两只猴子所经过的路程相等,这棵树高有多少米?树顶D到池塘A的距离有多少米?
19.(10分)如图,一块草坪的形状为四边形ABCD,其中,,,,,求这块草坪的面积.
20.(12分)阅读材料:
勾股定理本身就是一个关于a、b、c的方程,我们知道这个方程有无数组解,满足该方程的正整数解通常叫做勾股数组,关于勾股数组的研究我国历史上有非常辉煌的成就,根据《周髀算经》记载,在约公元前1100年,人们就已经知道“勾广三、股修四、径隅五”(古人把较短的直角边称为勾,较长的直角边称为股,而斜边则为弦),即知道了勾股数组.类似地,还可以得到下列勾股数组:,,,…,等等,这些数组也叫做毕达哥拉斯勾股数组,上述勾股数组的规律,可以用下面表格直观表示:
勾股数组 各数组的和 和的另一表示法 和与最小数的差 股 弦
3,4,5 12
5,12,13 30
7,24,25 56
观察分析上述勾股数组,可以看出它们具有如下特点:
特点1:最小的勾股数的平方等于另两个勾股数的和;
特点2:______.
…
回答问题:
(1)请你再写出上述勾股数组的一个特点:______;
(2)如果n表示比1大的奇数,则上述勾股数组可以表示为;
(3)请你证明(2)中的三个式子是勾股数组.
21.(12分)勾股定理神秘而美妙,它证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现;当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中,求证:.
证明:连接DB,过点D作交BC的延线于点F,则.
又
∴
∴
请参照上述证法,利用图2完成下面的证明:
将两个全等的直角三角形按图2所示摆放,其中.求证:.
答案以及解析
1.答案:C
解析:设芦苇的长度是x尺,
由题意可得,,
故选:C.
2.答案:D
解析:根据图形,直角三角形的边长的平方刚好为对应正方形的面积,
∴直角三角形的斜边平方为169,一条直角边的平方为144,
∴另一条直角边的平方为,
∴最小正方形A的面积是25,边长为5;
故选:D.
3.答案:C
解析:由题意得:,
∴
∵,,
∴(负值舍去)
∴
∴小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了8米
故选:C.
4.答案:B
解析:设,则,
又,
在中,,
得:
解得:
故选:B.
5.答案:C
解析:四边形ABCD是矩形,
,
由折叠的性质可得:;
在与中
(AAS)
设,则,,在直角三角形ABE中,由勾股定理得:
解得
故选:C.
6.答案:C
解析:设,过D作于E,
则,,.
在中,
,即,
解得.
故门的宽度(两扇门的和)AB为101寸.
故选:C.
7.答案:C
解析:如图,作出每一个三角形长度为8的边上的高,根据垂线段最短可得选项A、B、D中,长度为8的边上的高都小于6;
选项C中,因,这个三角形为直角三角形,所以长度为8的边上的高为6,
因此在这4个选项中,底都为8时,选项C的高最大,所以选项C的面积最大,
故选:C.
.
8.答案:C
解析:如图所示,延长交于G,
方法一:将五边形看成是由正方形与,拼成,则;
方法二:将五边形看成是由正方形,正方形,,拼成,则,
根据面积相等可以得到,即,
故选:C.
9.答案:B
解析:如图,连接AD,BE,
根据题意得:,,,
,,,
∴,,,
∴,,
∴,
∴.
故选:B.
10.答案:A
解析:∵正方形的面积为28,
∴,
设,
∵,
∴,
在中,由勾股定理得,,
∴,
∴,
∵,,
∴,
∴,
∵“赵爽弦图”是由四个全等的直角三角形与中间的小正方形EFGH拼成的一个大正方形,
∴,
∴,
∴,
∴,,
∴,
∵,
,
,
,
,
,
∴,
故选:A.
11.答案:
解析:根据题意画出图形,折断处离地面的高度为x尺,则,,
在中,,即,
故答案为.
12.答案:
解析:由题意知:
,,,
在中,由勾股定理得:
.
故答案为:.
13.答案:139
解析:如图,正方形、正方形的面积分别为25、144,
正方形BCMN的面积为,,
阴影部分的面积为
故答案为:139.
14.答案:17,144,145
解析:①,,.
②,,.
③,,.
④,,……
则第n组勾股数的第一个数为:,第二个数为:,第三个数为:
,
第8组勾股数为:17,144,145,
故答案为:17,144,145.
15.答案:2.5
解析:∵,,,
,
,
由平行线间距离处处相等可得:,
∴,而,
设绳索AD的长为xm,则,,
在中,由勾股定理得:,
即,解得:,
即绳索AD的长是2.5m,
故答案为:2.5.
16.答案:
解析:由题意知,,,即,
由勾股定理得,,即,
解得,,
∴树折断处与地面的距离(即的长)为.
17.答案:(1)见解析
(2)见解析
解析:(1)
.
(2)如图,连接,相交于点O,连接.
四边形是矩形,
,,.
.
根据阿波罗尼奥斯定理,得,.
.
18.答案:树高7.5米,树顶D到池塘A的距离有12.5米
解析:设为x米,且存在,
即,,
在直角中,为斜边,
则,
即
解得,
米,
米米米,
答:树高7.5米,树顶D到池塘A的距离有12.5米
19.答案:这块草坪的面积为36平方厘米
解析:连接AC,
∵在中,,,,
∴,
,
,
∴,即是直角三角形,
∴草坪面积.
即这块草坪的面积为36平方厘米.
20.答案:(1)勾股数组的和等于最小的勾股数与比它大1的整数的乘积;(答案不唯一)
(2),;(3)证明见解析
解析:(1)上述勾股数组的一个特点:勾股数组的和等于最小的勾股数与比它大1的整数的乘积;
故答案为:勾股数组的和等于最小的勾股数与比它大1的整数的乘积;
(2)为最小的勾股数,
勾股数组的和为,
勾股数组的和与最小数的差为,
股为,弦为,
勾股数组可以表示为,
故答案为:,;
(3)证明:
,
即是勾股数组.
21.答案:见解析
解析:证明:如图,连接BD,过点B作DE边上的高BF,可得
,
.
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面、求这根芦苇的长度是多少尺?设芦苇的长度是x尺,根据题意,可列方程为( )
A. B.
C. D.
2.如图,分别以直角三角形的三边为边向外作三个正方形,较大两个正方形的面积分别为169和144,则最小正方形A的边长是( )
A.25 B.1 C.12 D.5
3.如图,在与水平面成角的斜坡上有两棵一样高的柳树,两棵树水平距离,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了( )米.
A.4 B.6 C.8 D.10
4.如图,当秋千静止时,踏板离地的垂直高度,将它往前推至C处时(即水平距离,),踏板离地的垂直高度,它的绳索始终拉直,则绳索的长是( )
A. B. C. D.
5.如图,已知矩形ABCD沿着直线BD折叠,使点C落在处,交AD于E,,,则DE的长为( )
A.3 B.4 C.5 D.6
6.在我国古代数学著作《九章算术》“勾股”章中有一题:“今有开门去阃(kǔn)一尺,不合二寸,问门广几何?”大意是说:如图,推开双门(和),门边缘D,C两点到门槛的距离为1尺(1尺寸),双门间的缝隙为2寸,那么门的宽度(两扇门的和)为( )
A.103寸 B.102寸 C.101寸 D.100寸
7.如图,有四个三角形,各有一边长为6,一边长为8,若第三边分别为6,8,10,12,则面积最大的三角形是( )
A. B.
C. D.
8.《勾股举隅》为梅文鼎研究中国传统勾股算术的著作,其中的主要成就是证明了勾股定理和对勾股算术算法进行了推广.书中的证明方法是将4个三边长分别为,,的全等直角三角形拼成如图1所示的五边形,然后通过添加辅助线,用面积法证明勾股定理.下面是小华给出的相关证明:
如图2,延长交_____①_____于点G. 用两种不同的方法表示五边形的面积S: 方法一:将五边形看成是由正方形与,拼成,则_____②_____. 方法二:将五边形看成是由_____③_____,正方形,,拼成,则. 根据面积相等可以得到_____④_____,即.
则下列说法错误的是( )
A.①代表 B.②代表
C.③代表正方形 D.④代表
9.如图所示的网格是正方形网格,和的顶点都是网格线交点,那么的度数为( )
A. B. C. D.
10.如图,四个全等的直角三角形与中间的小正方形拼成了一个大正方形,连结,若正方形的面积为28,.则的值是( )
A.3.5 B.4.5 C.5 D.5.5
二、填空题(每小题4分,共20分)
11.《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为_______________.
12.我国古代数学名著《算法统宗》有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,5尺人高曾记,仕女家人争蹴.良工高士素好奇,算出索长有几?”此问题可理解为:“如图,有一架秋千,当它静止时,踏板离地距离的长为1尺,将它向前水平推送10尺时,即尺,秋千踏板离地的距离和身高5尺的人一样高,秋千的绳索始终拉得很直,试问绳索有多长?”,设秋千的绳索长为x尺,根据题意可列方程为______.
13.如图,以的两条直角边和斜边为边长分别作正方形,其中正方形、正方形的面积分别为25、144,则阴影部分的面积为______.
14.观察下列几组勾股数:①3、4、5;②5、12、13;③7、24、25;④9、40、41;…根据上面的规律,写出第8组勾股数:______.
15.如图,一架秋千静止时,踏板离地的垂直高度,将它往前推送1.5m(水平距离)时,秋千的踏板离地的垂直高度,秋千的绳索始终拉直,则绳索AD的长是_____m.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)如图,大风把一棵树刮断,已知被刮断前树高,倒下后树干顶部离根部距离,求树折断处与地面的距离(即的长).
17.(8分)阅读下面材料,完成相应的任务.
阿波罗尼奥斯定理
阿波罗尼奥斯(约公元前262-190年),古希腊数学家,与欧几里得、阿基米德合称为古希腊亚历山大前期的三大数学家.阿波罗尼奥斯定理又称中线定理,其内容为三角形两边的平方和等于第三边的一半与第三边上的中线的平方和的两倍.
如图,在中,点D为的中点,根据阿波罗尼奥斯定理,可得.
下面是该定理的部分证明过程:
证明:如图,过点A作于点E.
在中,由勾股定理,得.
同理可得,.
点D为的中点,.
…
任务:
(1)按照上面的思路,将该定理剩余的证明过程补充完整;
(2)请利用阿波罗尼奥斯定理解决下面的问题:如图,已知点P为矩形内任意一点,求证:.
18.(10分)如图,有两只猴子在一棵树高的点B处,它们都要到A处的池塘去喝水,其中一只猴子沿树爬下走到离树处的池塘A处,另一只猴子爬到树顶D后直线跃向池塘的A处,如果两只猴子所经过的路程相等,这棵树高有多少米?树顶D到池塘A的距离有多少米?
19.(10分)如图,一块草坪的形状为四边形ABCD,其中,,,,,求这块草坪的面积.
20.(12分)阅读材料:
勾股定理本身就是一个关于a、b、c的方程,我们知道这个方程有无数组解,满足该方程的正整数解通常叫做勾股数组,关于勾股数组的研究我国历史上有非常辉煌的成就,根据《周髀算经》记载,在约公元前1100年,人们就已经知道“勾广三、股修四、径隅五”(古人把较短的直角边称为勾,较长的直角边称为股,而斜边则为弦),即知道了勾股数组.类似地,还可以得到下列勾股数组:,,,…,等等,这些数组也叫做毕达哥拉斯勾股数组,上述勾股数组的规律,可以用下面表格直观表示:
勾股数组 各数组的和 和的另一表示法 和与最小数的差 股 弦
3,4,5 12
5,12,13 30
7,24,25 56
观察分析上述勾股数组,可以看出它们具有如下特点:
特点1:最小的勾股数的平方等于另两个勾股数的和;
特点2:______.
…
回答问题:
(1)请你再写出上述勾股数组的一个特点:______;
(2)如果n表示比1大的奇数,则上述勾股数组可以表示为;
(3)请你证明(2)中的三个式子是勾股数组.
21.(12分)勾股定理神秘而美妙,它证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现;当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中,求证:.
证明:连接DB,过点D作交BC的延线于点F,则.
又
∴
∴
请参照上述证法,利用图2完成下面的证明:
将两个全等的直角三角形按图2所示摆放,其中.求证:.
答案以及解析
1.答案:C
解析:设芦苇的长度是x尺,
由题意可得,,
故选:C.
2.答案:D
解析:根据图形,直角三角形的边长的平方刚好为对应正方形的面积,
∴直角三角形的斜边平方为169,一条直角边的平方为144,
∴另一条直角边的平方为,
∴最小正方形A的面积是25,边长为5;
故选:D.
3.答案:C
解析:由题意得:,
∴
∵,,
∴(负值舍去)
∴
∴小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了8米
故选:C.
4.答案:B
解析:设,则,
又,
在中,,
得:
解得:
故选:B.
5.答案:C
解析:四边形ABCD是矩形,
,
由折叠的性质可得:;
在与中
(AAS)
设,则,,在直角三角形ABE中,由勾股定理得:
解得
故选:C.
6.答案:C
解析:设,过D作于E,
则,,.
在中,
,即,
解得.
故门的宽度(两扇门的和)AB为101寸.
故选:C.
7.答案:C
解析:如图,作出每一个三角形长度为8的边上的高,根据垂线段最短可得选项A、B、D中,长度为8的边上的高都小于6;
选项C中,因,这个三角形为直角三角形,所以长度为8的边上的高为6,
因此在这4个选项中,底都为8时,选项C的高最大,所以选项C的面积最大,
故选:C.
.
8.答案:C
解析:如图所示,延长交于G,
方法一:将五边形看成是由正方形与,拼成,则;
方法二:将五边形看成是由正方形,正方形,,拼成,则,
根据面积相等可以得到,即,
故选:C.
9.答案:B
解析:如图,连接AD,BE,
根据题意得:,,,
,,,
∴,,,
∴,,
∴,
∴.
故选:B.
10.答案:A
解析:∵正方形的面积为28,
∴,
设,
∵,
∴,
在中,由勾股定理得,,
∴,
∴,
∵,,
∴,
∴,
∵“赵爽弦图”是由四个全等的直角三角形与中间的小正方形EFGH拼成的一个大正方形,
∴,
∴,
∴,
∴,,
∴,
∵,
,
,
,
,
,
∴,
故选:A.
11.答案:
解析:根据题意画出图形,折断处离地面的高度为x尺,则,,
在中,,即,
故答案为.
12.答案:
解析:由题意知:
,,,
在中,由勾股定理得:
.
故答案为:.
13.答案:139
解析:如图,正方形、正方形的面积分别为25、144,
正方形BCMN的面积为,,
阴影部分的面积为
故答案为:139.
14.答案:17,144,145
解析:①,,.
②,,.
③,,.
④,,……
则第n组勾股数的第一个数为:,第二个数为:,第三个数为:
,
第8组勾股数为:17,144,145,
故答案为:17,144,145.
15.答案:2.5
解析:∵,,,
,
,
由平行线间距离处处相等可得:,
∴,而,
设绳索AD的长为xm,则,,
在中,由勾股定理得:,
即,解得:,
即绳索AD的长是2.5m,
故答案为:2.5.
16.答案:
解析:由题意知,,,即,
由勾股定理得,,即,
解得,,
∴树折断处与地面的距离(即的长)为.
17.答案:(1)见解析
(2)见解析
解析:(1)
.
(2)如图,连接,相交于点O,连接.
四边形是矩形,
,,.
.
根据阿波罗尼奥斯定理,得,.
.
18.答案:树高7.5米,树顶D到池塘A的距离有12.5米
解析:设为x米,且存在,
即,,
在直角中,为斜边,
则,
即
解得,
米,
米米米,
答:树高7.5米,树顶D到池塘A的距离有12.5米
19.答案:这块草坪的面积为36平方厘米
解析:连接AC,
∵在中,,,,
∴,
,
,
∴,即是直角三角形,
∴草坪面积.
即这块草坪的面积为36平方厘米.
20.答案:(1)勾股数组的和等于最小的勾股数与比它大1的整数的乘积;(答案不唯一)
(2),;(3)证明见解析
解析:(1)上述勾股数组的一个特点:勾股数组的和等于最小的勾股数与比它大1的整数的乘积;
故答案为:勾股数组的和等于最小的勾股数与比它大1的整数的乘积;
(2)为最小的勾股数,
勾股数组的和为,
勾股数组的和与最小数的差为,
股为,弦为,
勾股数组可以表示为,
故答案为:,;
(3)证明:
,
即是勾股数组.
21.答案:见解析
解析:证明:如图,连接BD,过点B作DE边上的高BF,可得
,
.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
