第一章 勾股定理单元质检卷(B卷) 八年级上册数学北师大版(2012)(含解析)
文档属性
| 名称 | 第一章 勾股定理单元质检卷(B卷) 八年级上册数学北师大版(2012)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-15 21:36:06 | ||
图片预览


文档简介
(2)勾股定理—八年级上册数学北师大版(2012)单元质检卷(B卷)
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.《九章算术》是中国传统数学最重要的著作,书中有一个关于门和竹竿的问题,简译为:今有一扇门,不知门的高和宽.另有一竹竿,也不知竹竿的长短.竹竿横着放时比门的宽长4尺,竹竿竖着放时比门的高长2尺,竹竿斜着放时与门的对角线恰好相等,求门的对角线长.若设门的对角线长为x尺,则可列方程为( )
A. B.
C. D.
2.下列几组线段中,不能组成直角三角形的是( )
A.5,12,13 B.6,8,10 C.7,24,25 D.8,25,27
3.放学后,彬彬先去同学晓华家写了一个小时的作业,然后才回到家里.已知学校A.晓华家B,彬彬家C的两两之间的距离如图所示,且晓华家B在学校A的正东方向,则彬彬家C在学校A的( )
A.正南方向 B.正东方向 C.正西方向 D.正北方向
4.如图,有一个水池,水面是边长为8尺的正方形,在水池中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,这根芦苇的长度是( )
A.7.5尺 B.8尺 C.8.5尺 D.9尺
5.在学习《直角三角形》这一章时,爱动脑筋的小明同学发现了一组有规律的勾股数,并将它们记录在如下的表格中.按照这个规律,当时,b的值是( )
a 3 5 7 9 11 …
b 4 12 24 40 60 …
c 5 13 25 41 61 …
A.611 B.612 C.613 D.614
6.下列说法中正确的是( )
A.已知a,b,c是三角形的三边,则
B.在直角三角形中两边和的平方等于第三边的平方
C.在中,,所以
D.在中,,所以
7.如图,网格中每个小正方形的边长都为1,是( ).
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
8.如图“赵爽弦图”是由四个全等的直角三角形拼成的图形,若大正方形的面积41,小正方形的面积是1,设直角三角形较长的直角边为b,较短的直角边为a,则的值是( )
A.9 B. 8 C.7 D.6
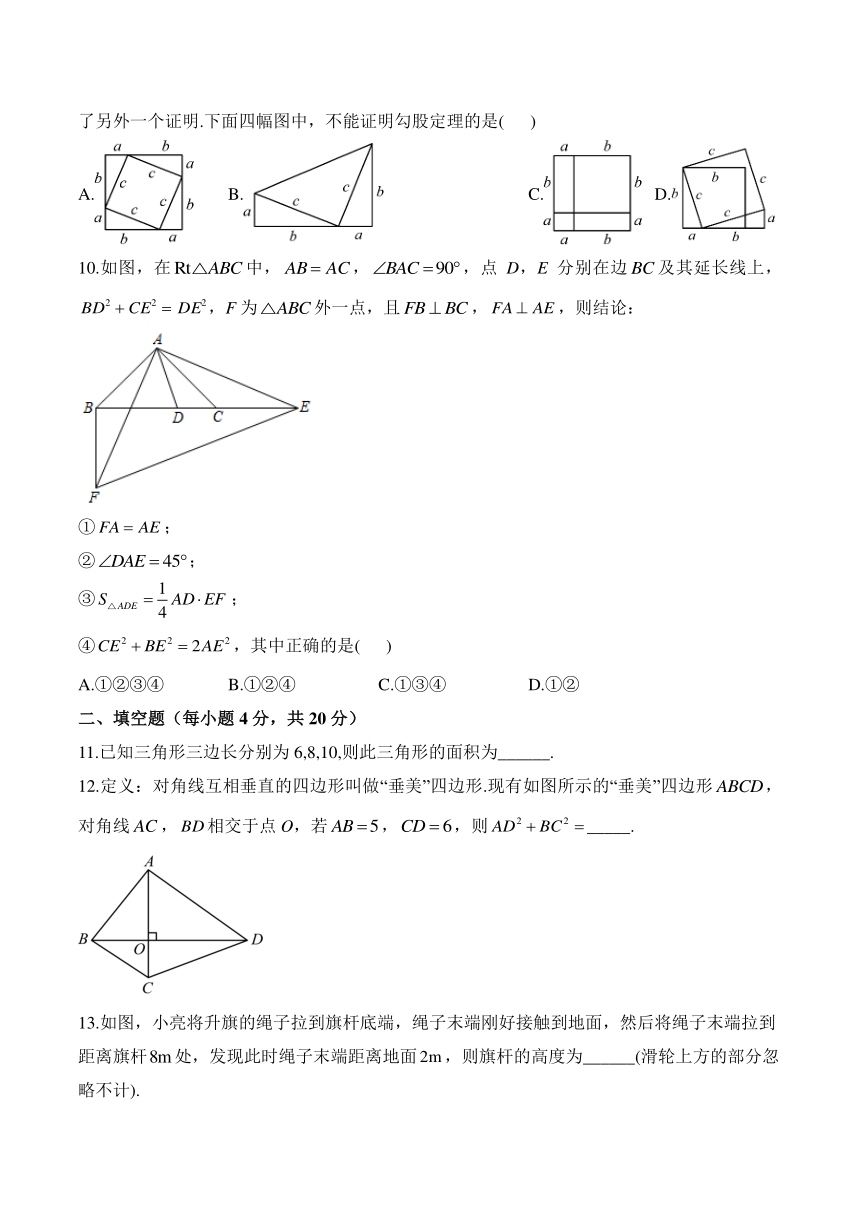
9.国是较早了解勾股定理的国家之一.据《周髀算经》记载,勾股定理的公式与证明是在西周由商高发现的,故又称之为“商高定理”;三国时代的蒋铭祖对勾股定理作出了详细注释,并给出了另外一个证明.下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
10.如图,在中,,,点D,E分别在边及其延长线上,,F为外一点,且,,则结论:
①;
②;
③;
④,其中正确的是( )
A.①②③④ B.①②④ C.①③④ D.①②
二、填空题(每小题4分,共20分)
11.已知三角形三边长分别为6,8,10,则此三角形的面积为______.
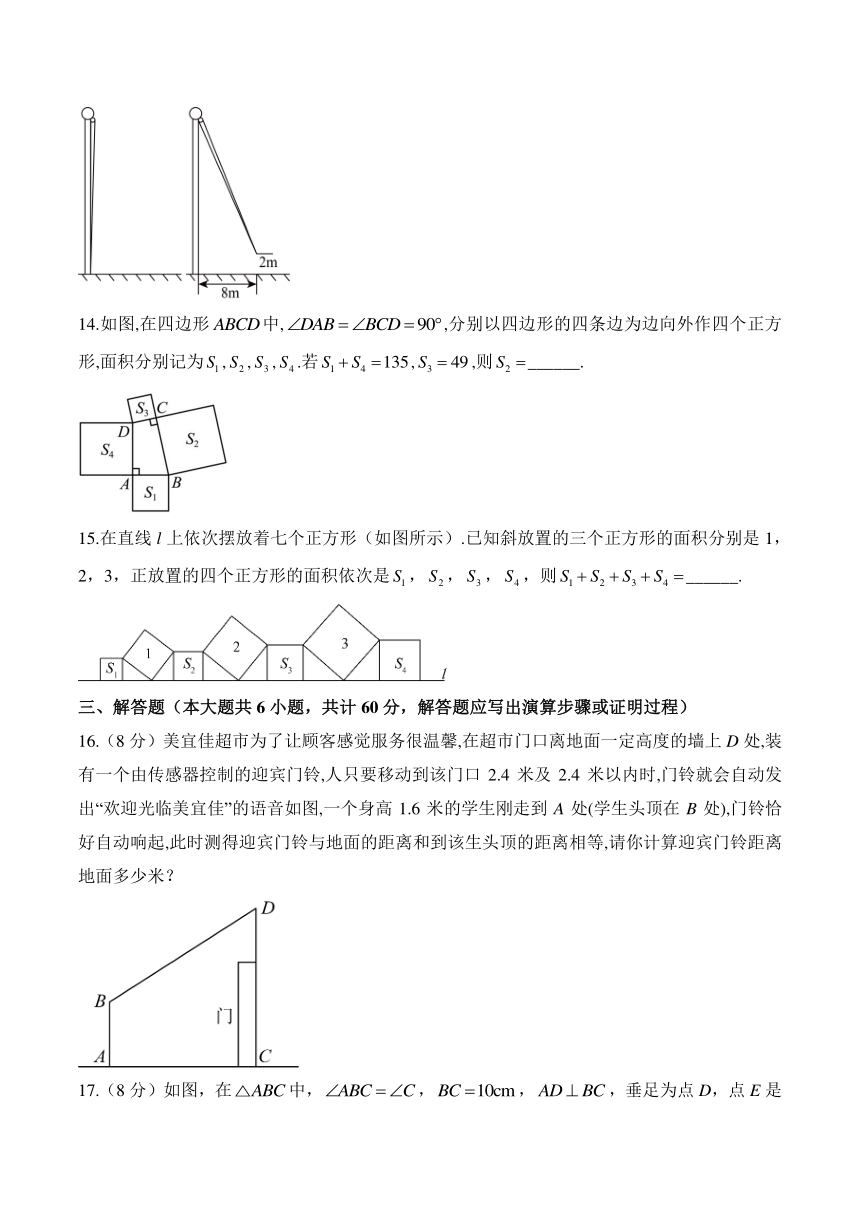
12.定义:对角线互相垂直的四边形叫做“垂美”四边形.现有如图所示的“垂美”四边形,对角线,相交于点O,若,,则_____.
13.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆处,发现此时绳子末端距离地面,则旗杆的高度为______(滑轮上方的部分忽略不计).
14.如图,在四边形中,,分别以四边形的四条边为边向外作四个正方形,面积分别记为,,,.若,,则______.
15.在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是,,,,则______.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)美宜佳超市为了让顾客感觉服务很温馨,在超市门口离地面一定高度的墙上D处,装有一个由传感器控制的迎宾门铃,人只要移动到该门口2.4米及2.4米以内时,门铃就会自动发出“欢迎光临美宜佳”的语音如图,一个身高1.6米的学生刚走到A处(学生头顶在B处),门铃恰好自动响起,此时测得迎宾门铃与地面的距离和到该生头顶的距离相等,请你计算迎宾门铃距离地面多少米?
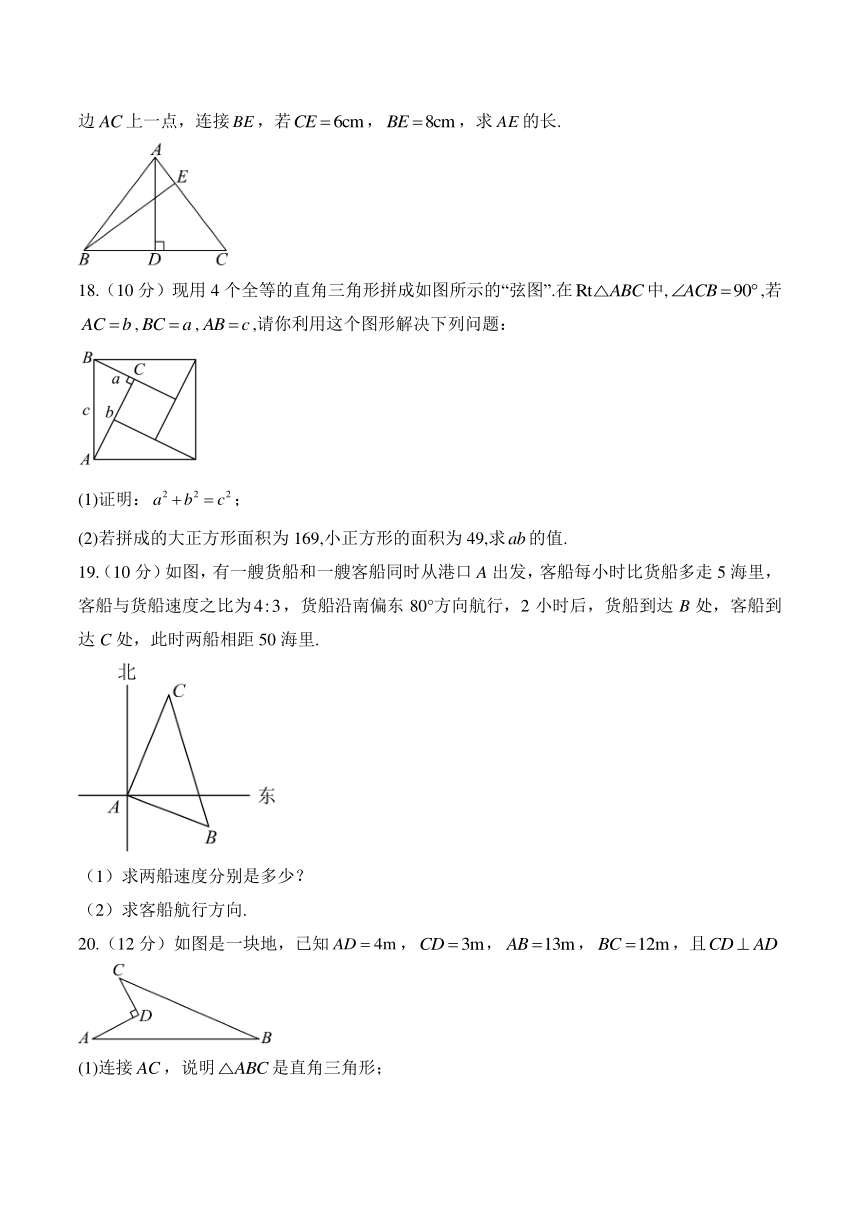
17.(8分)如图,在中,,,,垂足为点D,点E是边上一点,连接,若,,求的长.
18.(10分)现用4个全等的直角三角形拼成如图所示的“弦图”.在中,,若,,,请你利用这个图形解决下列问题:
(1)证明:;
(2)若拼成的大正方形面积为169,小正方形的面积为49,求的值.
19.(10分)如图,有一艘货船和一艘客船同时从港口A出发,客船每小时比货船多走5海里,客船与货船速度之比为,货船沿南偏东80°方向航行,2小时后,货船到达B处,客船到达C处,此时两船相距50海里.
(1)求两船速度分别是多少?
(2)求客船航行方向.
20.(12分)如图是一块地,已知,,,,且
(1)连接,说明是直角三角形;
(2)求这块地的面积
21.(12分)勾股定理的证明与计算
在勾股定理的学习过程中,我们已经学会了运用以下图形,验证著名的勾股定理,这种根据图形直观推论或验证数学规律和公式的方法,简称为“无字证明”.实际上它也可用于验证数与代数,图形与几何等领域中的许多数学公式和规律.
(1)右面图形都是用四个全等的直角三角形拼成一个正方形,从中选择一个图形证明勾股定理,写出证明过程.
(2)它体现的数学思想是( )
A.统计思想 B.分类思想 C.数形结合思想 D.函数思想
(3)如图,将两个全等的直角三角形按如图所示摆放,其中,求证:.
证明:如图所示:连接,过点B作,交延长线于点F,则请补全证明过程:
答案以及解析
1.答案:C
解析:设门的对角线长为x尺,则可列方程为:
故选:C.
2.答案:D
解析:A、,即能组成直角三角形,故本选项不合题意;
B、,即能组成直角三角形,故本选项不合题意;
C、,即能组成直角三角形,故本选项不合题意;
D、,即不能组成直角三角形,故本选项符合题意;
故选:D.
3.答案:D
解析:由图可得:,,,
,
是直角三角形,
彬彬家C在学校A的正北方向,
故选:D.
4.答案:C
解析:设芦苇的长度为x尺,则为尺,
根据勾股定理得:,
解得:,
芦苇的长度为8.5尺.
故选C.
5.答案:B
解析:由表格中的数据得:,,
∴,
∴当时,则,
解得:,
故选:B.
6.答案:C
解析:A.若该三角形不是直接三角形,则等式不成立,故本选项错误;
B.在直角三角形中,两直角边的平方和等于斜边的平方,故本选项错误;
C.在中,,a、b、c分别是,,的对边,则,故本选项正确;
D.在中,,a、b、c分别是,,的对边,则,故本选项错误;
故选C.
7.答案:A
解析:∵,,,,
,
即,,,
∴不是直角三角形,不是等腰三角形.
∵是钝角三角形,
∴是锐角三角形.
故选:A.
8.答案:A
解析:由题意可得,
解得 ,
或(不合题意,舍去)
即 ,
故选: A.
9.答案:C
解析:A.大正方形的面积为:,也可看作是4个直角三角形和一个小正方形组成,则其面积为:,,故本选项不符合题意;
B.梯形的面积为:,也可看作是2个直角三角形和一个等腰直角三角形组成,则其面积为:,,可以证明勾股定理,故本选项不符合题意;
C.图形中不涉及直角三角形,故无法证明勾股定理,故本选项符合题意;
D.图中图形面积等于边长为c的正方形面积,加上两个直角边分别为a、b的长方形面积,即其面积为:,也可看作是一个梯形面积加上一个等腰直角三角形的面积,则其面积为:,,故本选项不符合题意;
故选:C.
10.答案:A
解析:,,
,
,
,
,
,
,
,
,
,
即,
在和中
,
,
,故①正确;
连接,如图:
,
,
在中,,
,
,
,
,,
,
,
,故②正确;
延长交于H,如图:
,,
,,
,故③正确;
在中,,
,
,
,,
,
,故④正确,
综上所述,正确的有①②③④,
故选:A.
11.答案:24
解析:∵,
∴此三角形为直角三角形,
∴此三角形的面积为:.
故答案为:24.
12.答案:61
解析:∵是“垂美”四边形,
∴,
∴,
故答案为:61.
13.答案:
解析:设旗杆高度为,过点C作于B,
则,,
在中,
即,
解得:,即旗杆的高度为17米.
故答案为:.
14.答案:86
解析:如图,连接.
由题意,得,,,.
在中,由勾股定理得.
在中,由勾股定理得.
.
,
故答案为:86.
15.答案:4
解析:如图所示,根据题意可得:,
,
在和中
在中,,
,
,,,
同理可得:,
,
故答案:4.
16.答案:迎宾门铃距离地面2.6米
解析:由题意知,,,,,
如图,作于点E,则,,
设迎宾门铃距离地面x米,则,,
在中,由勾股定理得:,即,
解得:.
∴迎宾门铃距离地面2.6米.
17.答案:的长为
解析:,,
.
是直角三角形,且.
.
,
.
设,则.
在中,由勾股定理,得,
即,
解得,
的长为.
18.答案:(1)证明见解析
(2)
解析:(1)证明:大正方形的面积表示为,又可以表示为,
∴,
∴,
∴.
(2)∵大正方形的面积为169,
∴
∵小正方形的面积为49,
∴
∵大正方形的面积,
∴,
∴,
∴.
19.答案:(1)客船与货船的速度分别是20海里/小时和15海里/小时
(2)客船航行的方向为北偏东10°方向
解析:(1)设客船与货船的速度分别是海里/小时和海里/小时,依题意得,
.
解得,
,,
客船与货船的速度分别是20海里/小时和15海里/小时;
(2)由题可得,,,,
,
是直角三角形,且,
又货船沿南偏东方向航行,
客船航行的方向为北偏东方向.
20.答案:(1)见解析
(2)
解析:(1)
,
,
,
又,
;
,
,
又,
,
,
是直角三角形;
(2).
21.答案:(1)见解析
(2)C
(3)见解析
解析:(1)如图1所示,大正方形的边长为,则其面积为,
又由大正方形面积为四个全等的直角三角形的面积加上一个边长为c的正方形面积,即大正方形的面积为,
∴,
∴,
∴;
如图2所示,同理根据面积相等可得,
∴,
∴;
(2)根据题意可得它体现的数学思想是数形结合思想,
故选:C;
(3)如图所示:连接,过点B作,交延长线于点F,则,
∵,
∴,
∴,
∴,
∴,
∴.
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.《九章算术》是中国传统数学最重要的著作,书中有一个关于门和竹竿的问题,简译为:今有一扇门,不知门的高和宽.另有一竹竿,也不知竹竿的长短.竹竿横着放时比门的宽长4尺,竹竿竖着放时比门的高长2尺,竹竿斜着放时与门的对角线恰好相等,求门的对角线长.若设门的对角线长为x尺,则可列方程为( )
A. B.
C. D.
2.下列几组线段中,不能组成直角三角形的是( )
A.5,12,13 B.6,8,10 C.7,24,25 D.8,25,27
3.放学后,彬彬先去同学晓华家写了一个小时的作业,然后才回到家里.已知学校A.晓华家B,彬彬家C的两两之间的距离如图所示,且晓华家B在学校A的正东方向,则彬彬家C在学校A的( )
A.正南方向 B.正东方向 C.正西方向 D.正北方向
4.如图,有一个水池,水面是边长为8尺的正方形,在水池中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,这根芦苇的长度是( )
A.7.5尺 B.8尺 C.8.5尺 D.9尺
5.在学习《直角三角形》这一章时,爱动脑筋的小明同学发现了一组有规律的勾股数,并将它们记录在如下的表格中.按照这个规律,当时,b的值是( )
a 3 5 7 9 11 …
b 4 12 24 40 60 …
c 5 13 25 41 61 …
A.611 B.612 C.613 D.614
6.下列说法中正确的是( )
A.已知a,b,c是三角形的三边,则
B.在直角三角形中两边和的平方等于第三边的平方
C.在中,,所以
D.在中,,所以
7.如图,网格中每个小正方形的边长都为1,是( ).
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
8.如图“赵爽弦图”是由四个全等的直角三角形拼成的图形,若大正方形的面积41,小正方形的面积是1,设直角三角形较长的直角边为b,较短的直角边为a,则的值是( )
A.9 B. 8 C.7 D.6
9.国是较早了解勾股定理的国家之一.据《周髀算经》记载,勾股定理的公式与证明是在西周由商高发现的,故又称之为“商高定理”;三国时代的蒋铭祖对勾股定理作出了详细注释,并给出了另外一个证明.下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
10.如图,在中,,,点D,E分别在边及其延长线上,,F为外一点,且,,则结论:
①;
②;
③;
④,其中正确的是( )
A.①②③④ B.①②④ C.①③④ D.①②
二、填空题(每小题4分,共20分)
11.已知三角形三边长分别为6,8,10,则此三角形的面积为______.
12.定义:对角线互相垂直的四边形叫做“垂美”四边形.现有如图所示的“垂美”四边形,对角线,相交于点O,若,,则_____.
13.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆处,发现此时绳子末端距离地面,则旗杆的高度为______(滑轮上方的部分忽略不计).
14.如图,在四边形中,,分别以四边形的四条边为边向外作四个正方形,面积分别记为,,,.若,,则______.
15.在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是,,,,则______.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)美宜佳超市为了让顾客感觉服务很温馨,在超市门口离地面一定高度的墙上D处,装有一个由传感器控制的迎宾门铃,人只要移动到该门口2.4米及2.4米以内时,门铃就会自动发出“欢迎光临美宜佳”的语音如图,一个身高1.6米的学生刚走到A处(学生头顶在B处),门铃恰好自动响起,此时测得迎宾门铃与地面的距离和到该生头顶的距离相等,请你计算迎宾门铃距离地面多少米?
17.(8分)如图,在中,,,,垂足为点D,点E是边上一点,连接,若,,求的长.
18.(10分)现用4个全等的直角三角形拼成如图所示的“弦图”.在中,,若,,,请你利用这个图形解决下列问题:
(1)证明:;
(2)若拼成的大正方形面积为169,小正方形的面积为49,求的值.
19.(10分)如图,有一艘货船和一艘客船同时从港口A出发,客船每小时比货船多走5海里,客船与货船速度之比为,货船沿南偏东80°方向航行,2小时后,货船到达B处,客船到达C处,此时两船相距50海里.
(1)求两船速度分别是多少?
(2)求客船航行方向.
20.(12分)如图是一块地,已知,,,,且
(1)连接,说明是直角三角形;
(2)求这块地的面积
21.(12分)勾股定理的证明与计算
在勾股定理的学习过程中,我们已经学会了运用以下图形,验证著名的勾股定理,这种根据图形直观推论或验证数学规律和公式的方法,简称为“无字证明”.实际上它也可用于验证数与代数,图形与几何等领域中的许多数学公式和规律.
(1)右面图形都是用四个全等的直角三角形拼成一个正方形,从中选择一个图形证明勾股定理,写出证明过程.
(2)它体现的数学思想是( )
A.统计思想 B.分类思想 C.数形结合思想 D.函数思想
(3)如图,将两个全等的直角三角形按如图所示摆放,其中,求证:.
证明:如图所示:连接,过点B作,交延长线于点F,则请补全证明过程:
答案以及解析
1.答案:C
解析:设门的对角线长为x尺,则可列方程为:
故选:C.
2.答案:D
解析:A、,即能组成直角三角形,故本选项不合题意;
B、,即能组成直角三角形,故本选项不合题意;
C、,即能组成直角三角形,故本选项不合题意;
D、,即不能组成直角三角形,故本选项符合题意;
故选:D.
3.答案:D
解析:由图可得:,,,
,
是直角三角形,
彬彬家C在学校A的正北方向,
故选:D.
4.答案:C
解析:设芦苇的长度为x尺,则为尺,
根据勾股定理得:,
解得:,
芦苇的长度为8.5尺.
故选C.
5.答案:B
解析:由表格中的数据得:,,
∴,
∴当时,则,
解得:,
故选:B.
6.答案:C
解析:A.若该三角形不是直接三角形,则等式不成立,故本选项错误;
B.在直角三角形中,两直角边的平方和等于斜边的平方,故本选项错误;
C.在中,,a、b、c分别是,,的对边,则,故本选项正确;
D.在中,,a、b、c分别是,,的对边,则,故本选项错误;
故选C.
7.答案:A
解析:∵,,,,
,
即,,,
∴不是直角三角形,不是等腰三角形.
∵是钝角三角形,
∴是锐角三角形.
故选:A.
8.答案:A
解析:由题意可得,
解得 ,
或(不合题意,舍去)
即 ,
故选: A.
9.答案:C
解析:A.大正方形的面积为:,也可看作是4个直角三角形和一个小正方形组成,则其面积为:,,故本选项不符合题意;
B.梯形的面积为:,也可看作是2个直角三角形和一个等腰直角三角形组成,则其面积为:,,可以证明勾股定理,故本选项不符合题意;
C.图形中不涉及直角三角形,故无法证明勾股定理,故本选项符合题意;
D.图中图形面积等于边长为c的正方形面积,加上两个直角边分别为a、b的长方形面积,即其面积为:,也可看作是一个梯形面积加上一个等腰直角三角形的面积,则其面积为:,,故本选项不符合题意;
故选:C.
10.答案:A
解析:,,
,
,
,
,
,
,
,
,
,
即,
在和中
,
,
,故①正确;
连接,如图:
,
,
在中,,
,
,
,
,,
,
,
,故②正确;
延长交于H,如图:
,,
,,
,故③正确;
在中,,
,
,
,,
,
,故④正确,
综上所述,正确的有①②③④,
故选:A.
11.答案:24
解析:∵,
∴此三角形为直角三角形,
∴此三角形的面积为:.
故答案为:24.
12.答案:61
解析:∵是“垂美”四边形,
∴,
∴,
故答案为:61.
13.答案:
解析:设旗杆高度为,过点C作于B,
则,,
在中,
即,
解得:,即旗杆的高度为17米.
故答案为:.
14.答案:86
解析:如图,连接.
由题意,得,,,.
在中,由勾股定理得.
在中,由勾股定理得.
.
,
故答案为:86.
15.答案:4
解析:如图所示,根据题意可得:,
,
在和中
在中,,
,
,,,
同理可得:,
,
故答案:4.
16.答案:迎宾门铃距离地面2.6米
解析:由题意知,,,,,
如图,作于点E,则,,
设迎宾门铃距离地面x米,则,,
在中,由勾股定理得:,即,
解得:.
∴迎宾门铃距离地面2.6米.
17.答案:的长为
解析:,,
.
是直角三角形,且.
.
,
.
设,则.
在中,由勾股定理,得,
即,
解得,
的长为.
18.答案:(1)证明见解析
(2)
解析:(1)证明:大正方形的面积表示为,又可以表示为,
∴,
∴,
∴.
(2)∵大正方形的面积为169,
∴
∵小正方形的面积为49,
∴
∵大正方形的面积,
∴,
∴,
∴.
19.答案:(1)客船与货船的速度分别是20海里/小时和15海里/小时
(2)客船航行的方向为北偏东10°方向
解析:(1)设客船与货船的速度分别是海里/小时和海里/小时,依题意得,
.
解得,
,,
客船与货船的速度分别是20海里/小时和15海里/小时;
(2)由题可得,,,,
,
是直角三角形,且,
又货船沿南偏东方向航行,
客船航行的方向为北偏东方向.
20.答案:(1)见解析
(2)
解析:(1)
,
,
,
又,
;
,
,
又,
,
,
是直角三角形;
(2).
21.答案:(1)见解析
(2)C
(3)见解析
解析:(1)如图1所示,大正方形的边长为,则其面积为,
又由大正方形面积为四个全等的直角三角形的面积加上一个边长为c的正方形面积,即大正方形的面积为,
∴,
∴,
∴;
如图2所示,同理根据面积相等可得,
∴,
∴;
(2)根据题意可得它体现的数学思想是数形结合思想,
故选:C;
(3)如图所示:连接,过点B作,交延长线于点F,则,
∵,
∴,
∴,
∴,
∴,
∴.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
