第一章 直角三角形的边角关系单元质检卷(A卷) 九年级下册数学北师大版(2012)(含解析)
文档属性
| 名称 | 第一章 直角三角形的边角关系单元质检卷(A卷) 九年级下册数学北师大版(2012)(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-15 00:00:00 | ||
图片预览

文档简介
(1)直角三角形的边角关系—九年级下册数学北师大版(2012)单元质检卷(A卷)
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
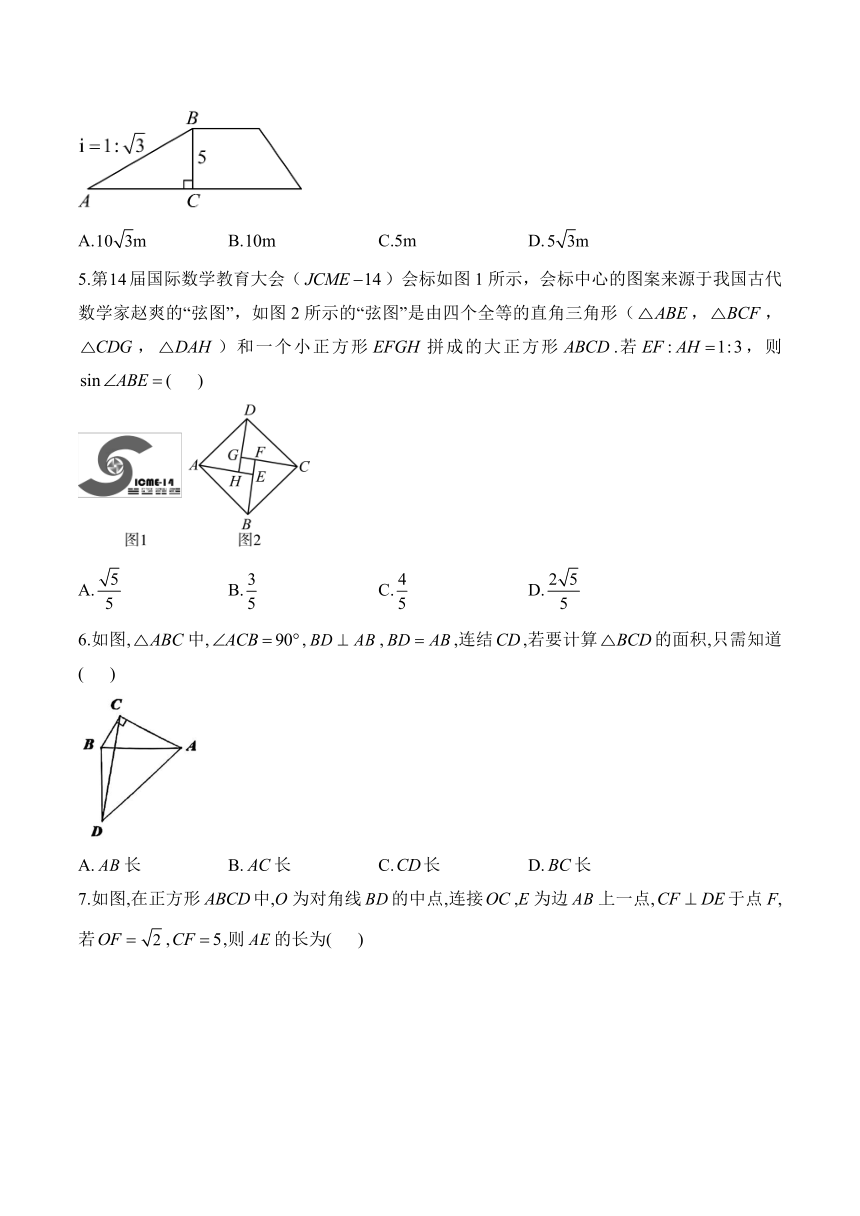
1.如图,在中,已知,,则的长为( )
A. B. C. D.
2.如图,在的正方形网格中,每个小正方形的边长都是1,的顶点都在这些小正方形的顶点上,则的值为( )
A. B. C. D.
3.如图,在平面直角坐标系中,菱形的顶点A,B,C在坐标轴上,若点A的坐标为,,则菱形的周长为( )
A.13 B.14 C.15 D.
4.如图,某地一座建筑物的截面图的高,坡面的坡度为,则的长为( )
A. B. C.5m D.
5.第届国际数学教育大会()会标如图1所示,会标中心的图案来源于我国古代数学家赵爽的“弦图”,如图2所示的“弦图”是由四个全等的直角三角形(,,,)和一个小正方形拼成的大正方形.若,则( )
A. B. C. D.
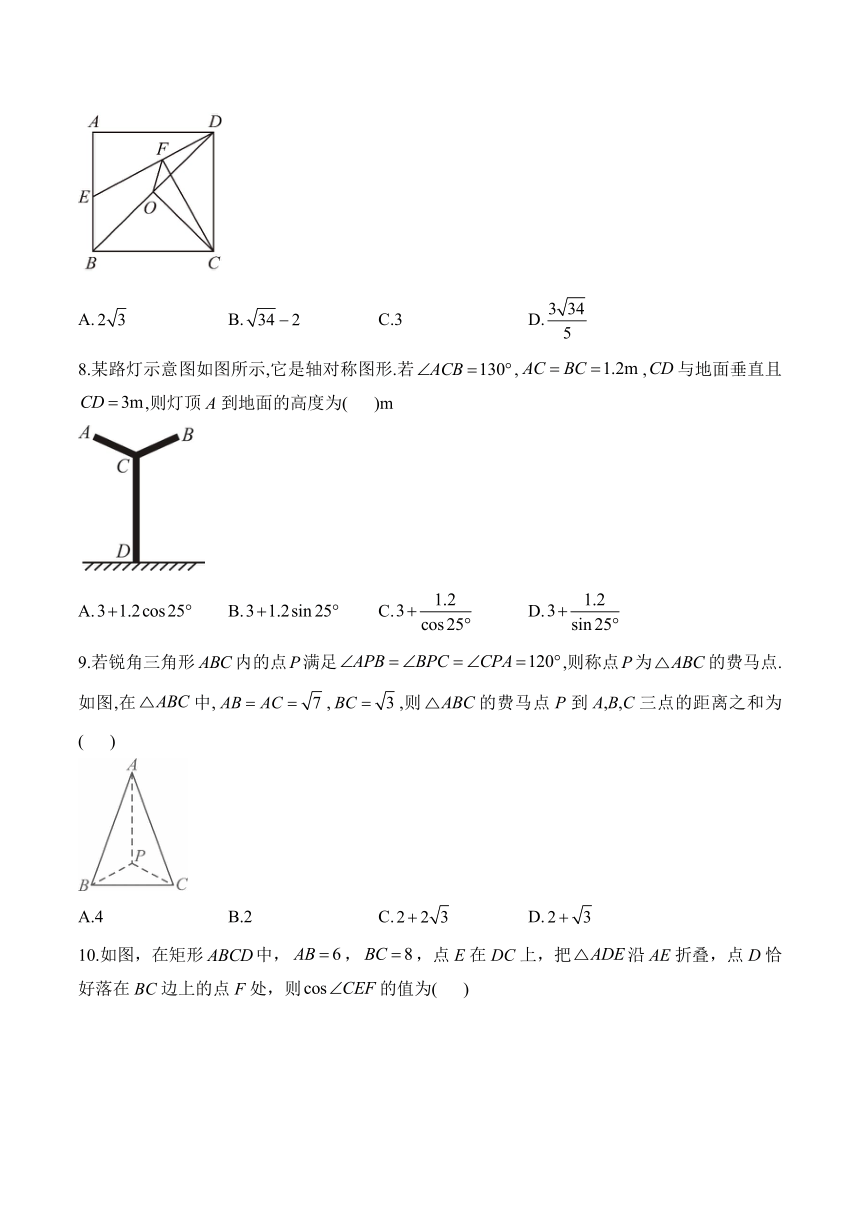
6.如图,中,,,,连结,若要计算的面积,只需知道( )
A.长 B.长 C.长 D.长
7.如图,在正方形中,O为对角线的中点,连接,E为边上一点,于点F,若,,则的长为( )
A. B. C.3 D.
8.某路灯示意图如图所示,它是轴对称图形.若,,与地面垂直且,则灯顶A到地面的高度为( )m
A. B. C. D.
9.若锐角三角形内的点P满足,则称点P为的费马点.如图,在中,,,则的费马点P到A,B,C三点的距离之和为( )
A.4 B.2 C. D.
10.如图,在矩形中,,,点E在DC上,把沿AE折叠,点D恰好落在BC边上的点F处,则的值为( )
A. B. C. D.
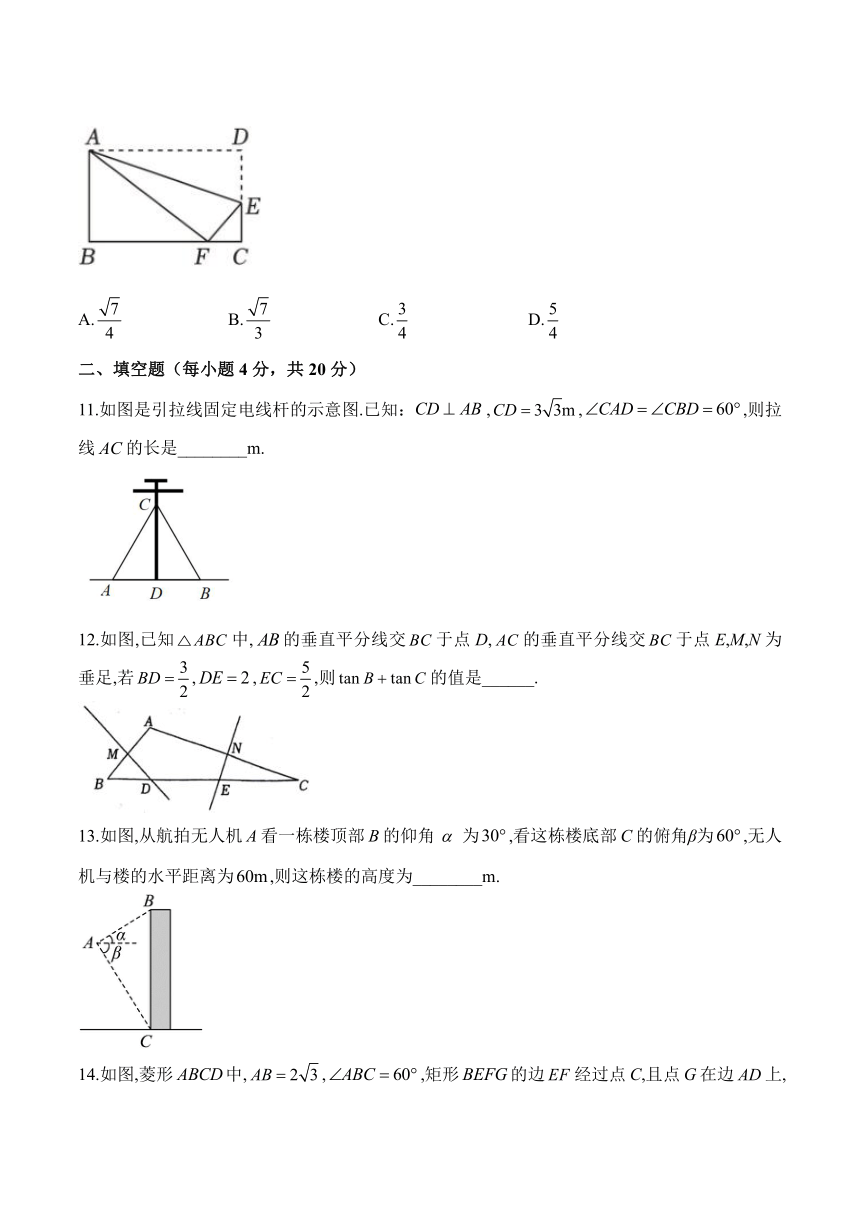
二、填空题(每小题4分,共20分)
11.如图是引拉线固定电线杆的示意图.已知:,,,则拉线的长是________m.
12.如图,已知中,的垂直平分线交于点D,的垂直平分线交于点E,M,N为垂足,若,,,则的值是______.
13.如图,从航拍无人机A看一栋楼顶部B的仰角为,看这栋楼底部C的俯角β为,无人机与楼的水平距离为,则这栋楼的高度为________m.
14.如图,菱形中,,,矩形的边经过点C,且点G在边上,若,则的长为______.
15.小慧同学在学习“图形的相似”一章后,发现学习内容是一个逐步特殊化的过程,请在横线上填写适当的数值__________,感受这种特殊化的学习过程;在“特殊线段比”的条件下,已知,,点D在上,若,,,则__________°.
比例中项:若,则b就是a、c的比例中项.:
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)计算:
17.(8分)如图,在中,,是边上的中线,,,.
(1)求的长;
(2)求的值.
18.(10分)某小区门口安装了汽车出入道闸.道闸关闭时,如图1,四边形为矩形,长3米,长1米,点C与点N重合.道闸打开的过程中,边固定,连杆,分别绕点A,B转动,且边始终与边平行.
(1)如图2,当道闸打开至时,边上一点P到地面的距离PE为1米,求点P到的距离的长.
(2)一辆轿车过道闸,已知轿车宽1.8米,高1.6米.当道闸打开至时,轿车能否驶入小区?请说明理由,(参考数据:,,)
19.(10分)半挂车是挂车中的一种类型,是通过牵引销与半挂车头相连接的一种重型运输交通工具.如图是一种轻体侧翻自卸半挂车.图1是半挂车拉货状态截面示意图,图2是其卸货状态截面示意图,四边形为矩形,已知该车的车厢长为13米,宽为2.5米.高为2米,车板离地的距离为1米.请你计算:
(1)该半挂车的车厢容积为______立方米;
(2)该半挂车卸货时,车身侧翻,侧翻角度为可全部卸完货物,求此时车身最高点离地面的距离.(参考数据:,,,结果保留一位小数.)
20.(12分)陕甘边革命根据地照金纪念馆广场上屹立着三位革命家的塑像,高高矗立,身姿伟岸.某数学兴趣小组计划在假期前往照金革命根据地学习,并测量塑像高度,活动方案如下:
测量方案:如图,点B、E、F、D四点在同一条直线上,在点E处放置平面镜,此时小明视线刚好在平面镜内看到塑像顶端C的像,在点F处安装测倾器,测得塑像顶端C的仰角约为51.F3°.
数据收集:测得眼睛离地面高度米,米,米,米,,,.
解决问题:求塑像的高度.(结果精确到0.1米;参考数据:,,)
21.(12分)图1是一种手机自拍杆,杆体从上至下分别由手机夹架、多节套管和可升降支架脚连接而成.使用时通过自由伸缩套管调节自拍杆的长度,同时可以通过调节支架脚使拍摄时更灵活安全.图2是其正面简化示意图,手机(为矩形)与其下方套管连接于点E,E为的中点,,支架脚,与地面平行,.
(1)当时,求点E到地面的高度;
(2)若在某环境中拍摄时,调节支架脚使,若,求点G到直线与交点的距离.
(参考数据:,,,,结果精确到)
答案以及解析
1.答案:C
解析:∵在中,,,
∴;
故选C.
2.答案:D
解析:如图,过C作于D,则,
.
.
故选D.
3.答案:D
解析:∵四边形是菱形,,
∴,,
∵点A的坐标为,
∴,
在中,,
∴菱形的周长为,
故选:D.
4.答案:B
解析:∵坡面的坡度为,
∴,
∴,
在中,,
∴,
故选:B.
5.答案:C
解析:根据题意,设,则,
,四边形为正方形,
,,
,
,
,
,
故选:C.
6.答案:D
解析:过C作于F,
∵,,
∴,
∴,
∴,
∴,
∵,
∴的面积为,
故选∶D.
7.答案:D
解析:如图所示,过点O作交于点G,
∵O为正方形对角线的中点,
∴,
∴
∵
∴
又∵,
∴
∴
∴,
∴
又∵
∴
∴
∵
∴
∴
故选:D.
8.答案:B
解析:如图,过点E作于点E,过点C作于点M,
所以,四边形是矩形,
∴,
∵路灯图是轴对称图形,且,
∵
在中,,
又
∴,
∴
即灯顶A到地面的高度为
故选:B.
9.答案:A
解析:过A作于点D,过B,C分别作,
∵是等腰三角形,
∴,
∴,
∴点P是的费马点,
∵,,
∴,
∴,,
在中,由勾股定理得:,
∴,
∴,
即的费马点P到A,B,C三点的距离之和为4,
故选:A.
10.答案:A
解析:四边形ABCD是矩形,
,,
把沿AE折叠,点D恰好落在BC边上的点F处,
,,
,
,
在中,
,
由勾股定理,得,
,
,
,
,
故选:A.
11.答案:6
解析:在直角中,,
则.
答:拉线AC的长是6.
12.答案:/
解析:连接,,
∵,,
∴,
∵的垂直平分线交于点D,的垂直平分线交于点E,
∴,,
∵,
∴,
∴是直角三角形,
∴,
∴
.
故答案为:.
13.答案:
解析:如图,作于点D,则,
在中,,
,
在中,,
,
,
即这栋楼的高度为,
故答案为:.
14.答案:
解析:过点G作于点M,过点C作于点N,
则,
∵四边形为菱形,
∴,,,
∴,
∴四边形为矩形,
∴,
在中,,,
∴,
∴,
∵四边形为矩形,
∴,,
∴,
又∵,
∴,
∴,
∴,
∴,
故答案为:.
15.答案:3;30或90
解析:,
,,
;
当点D在线段上时,如图所示:
,
,,,,
,,
,,
;
当点D在射线上时,如图所示:
,
同理可得,,
;
当点D在射线上时,不成立,
综上所述,或,
故答案为:3;30或90.
16.答案:
解析:原式
.
17.答案:(1)14
(2)
解析:(1)在中,,,
,
在中,,
,
;
(2)是边上的中线,
,
,
,
.
18.答案:(1)2
(2)轿车能驶入小区,理由见解析
解析:(1)在中,
∵,,
∴,
∵,
∴,
(2)当时,,则,
在中,
,
∴,
∴,
∴,
∵,
∴轿车能驶入小区.
19.答案:(1)65
(2)4.2米
解析:(1)根据题意,得,
故答案为:65.
(2)过点D作于点F,交于点M,交于点G,
则,
∵四边形为矩形,
∴,,,
∴,
∵,
∴四边形为矩形,
∴,
∵,,
∴,
∴,,
∴,
∴,
∴,
20.答案:6.4米
解析:过点G作,垂足为点H,如图所示:
由题意得:,米,,
设米,
米,
米,
在中,
米
米,
,
,
,
,
,
解得:,
经检验:是原方程的根,
∴(米),
∴塑像的高度为6.4米.
21.答案:(1)点E到地面的高度
(2)点G到直线与交点的距离约为
解析:(1)如图,设EF与GH的交点为点M
,
,即
,
在中,
答:点E到地面的高度;
(2)由(1)已知,
(等腰三角形的三线合一)
,即
则依题意,延长AB分别交GF于点P,交GH于点Q,画图如下所示:
四边形ABCD是矩形
,即
,即
又
四边形BEMQ是平行四边形
平行四边形BEMQ是矩形
,点E是BC的中点
在中,,即
解得
答:点G到直线与交点的距离约为.
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.如图,在中,已知,,则的长为( )
A. B. C. D.
2.如图,在的正方形网格中,每个小正方形的边长都是1,的顶点都在这些小正方形的顶点上,则的值为( )
A. B. C. D.
3.如图,在平面直角坐标系中,菱形的顶点A,B,C在坐标轴上,若点A的坐标为,,则菱形的周长为( )
A.13 B.14 C.15 D.
4.如图,某地一座建筑物的截面图的高,坡面的坡度为,则的长为( )
A. B. C.5m D.
5.第届国际数学教育大会()会标如图1所示,会标中心的图案来源于我国古代数学家赵爽的“弦图”,如图2所示的“弦图”是由四个全等的直角三角形(,,,)和一个小正方形拼成的大正方形.若,则( )
A. B. C. D.
6.如图,中,,,,连结,若要计算的面积,只需知道( )
A.长 B.长 C.长 D.长
7.如图,在正方形中,O为对角线的中点,连接,E为边上一点,于点F,若,,则的长为( )
A. B. C.3 D.
8.某路灯示意图如图所示,它是轴对称图形.若,,与地面垂直且,则灯顶A到地面的高度为( )m
A. B. C. D.
9.若锐角三角形内的点P满足,则称点P为的费马点.如图,在中,,,则的费马点P到A,B,C三点的距离之和为( )
A.4 B.2 C. D.
10.如图,在矩形中,,,点E在DC上,把沿AE折叠,点D恰好落在BC边上的点F处,则的值为( )
A. B. C. D.
二、填空题(每小题4分,共20分)
11.如图是引拉线固定电线杆的示意图.已知:,,,则拉线的长是________m.
12.如图,已知中,的垂直平分线交于点D,的垂直平分线交于点E,M,N为垂足,若,,,则的值是______.
13.如图,从航拍无人机A看一栋楼顶部B的仰角为,看这栋楼底部C的俯角β为,无人机与楼的水平距离为,则这栋楼的高度为________m.
14.如图,菱形中,,,矩形的边经过点C,且点G在边上,若,则的长为______.
15.小慧同学在学习“图形的相似”一章后,发现学习内容是一个逐步特殊化的过程,请在横线上填写适当的数值__________,感受这种特殊化的学习过程;在“特殊线段比”的条件下,已知,,点D在上,若,,,则__________°.
比例中项:若,则b就是a、c的比例中项.:
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)计算:
17.(8分)如图,在中,,是边上的中线,,,.
(1)求的长;
(2)求的值.
18.(10分)某小区门口安装了汽车出入道闸.道闸关闭时,如图1,四边形为矩形,长3米,长1米,点C与点N重合.道闸打开的过程中,边固定,连杆,分别绕点A,B转动,且边始终与边平行.
(1)如图2,当道闸打开至时,边上一点P到地面的距离PE为1米,求点P到的距离的长.
(2)一辆轿车过道闸,已知轿车宽1.8米,高1.6米.当道闸打开至时,轿车能否驶入小区?请说明理由,(参考数据:,,)
19.(10分)半挂车是挂车中的一种类型,是通过牵引销与半挂车头相连接的一种重型运输交通工具.如图是一种轻体侧翻自卸半挂车.图1是半挂车拉货状态截面示意图,图2是其卸货状态截面示意图,四边形为矩形,已知该车的车厢长为13米,宽为2.5米.高为2米,车板离地的距离为1米.请你计算:
(1)该半挂车的车厢容积为______立方米;
(2)该半挂车卸货时,车身侧翻,侧翻角度为可全部卸完货物,求此时车身最高点离地面的距离.(参考数据:,,,结果保留一位小数.)
20.(12分)陕甘边革命根据地照金纪念馆广场上屹立着三位革命家的塑像,高高矗立,身姿伟岸.某数学兴趣小组计划在假期前往照金革命根据地学习,并测量塑像高度,活动方案如下:
测量方案:如图,点B、E、F、D四点在同一条直线上,在点E处放置平面镜,此时小明视线刚好在平面镜内看到塑像顶端C的像,在点F处安装测倾器,测得塑像顶端C的仰角约为51.F3°.
数据收集:测得眼睛离地面高度米,米,米,米,,,.
解决问题:求塑像的高度.(结果精确到0.1米;参考数据:,,)
21.(12分)图1是一种手机自拍杆,杆体从上至下分别由手机夹架、多节套管和可升降支架脚连接而成.使用时通过自由伸缩套管调节自拍杆的长度,同时可以通过调节支架脚使拍摄时更灵活安全.图2是其正面简化示意图,手机(为矩形)与其下方套管连接于点E,E为的中点,,支架脚,与地面平行,.
(1)当时,求点E到地面的高度;
(2)若在某环境中拍摄时,调节支架脚使,若,求点G到直线与交点的距离.
(参考数据:,,,,结果精确到)
答案以及解析
1.答案:C
解析:∵在中,,,
∴;
故选C.
2.答案:D
解析:如图,过C作于D,则,
.
.
故选D.
3.答案:D
解析:∵四边形是菱形,,
∴,,
∵点A的坐标为,
∴,
在中,,
∴菱形的周长为,
故选:D.
4.答案:B
解析:∵坡面的坡度为,
∴,
∴,
在中,,
∴,
故选:B.
5.答案:C
解析:根据题意,设,则,
,四边形为正方形,
,,
,
,
,
,
故选:C.
6.答案:D
解析:过C作于F,
∵,,
∴,
∴,
∴,
∴,
∵,
∴的面积为,
故选∶D.
7.答案:D
解析:如图所示,过点O作交于点G,
∵O为正方形对角线的中点,
∴,
∴
∵
∴
又∵,
∴
∴
∴,
∴
又∵
∴
∴
∵
∴
∴
故选:D.
8.答案:B
解析:如图,过点E作于点E,过点C作于点M,
所以,四边形是矩形,
∴,
∵路灯图是轴对称图形,且,
∵
在中,,
又
∴,
∴
即灯顶A到地面的高度为
故选:B.
9.答案:A
解析:过A作于点D,过B,C分别作,
∵是等腰三角形,
∴,
∴,
∴点P是的费马点,
∵,,
∴,
∴,,
在中,由勾股定理得:,
∴,
∴,
即的费马点P到A,B,C三点的距离之和为4,
故选:A.
10.答案:A
解析:四边形ABCD是矩形,
,,
把沿AE折叠,点D恰好落在BC边上的点F处,
,,
,
,
在中,
,
由勾股定理,得,
,
,
,
,
故选:A.
11.答案:6
解析:在直角中,,
则.
答:拉线AC的长是6.
12.答案:/
解析:连接,,
∵,,
∴,
∵的垂直平分线交于点D,的垂直平分线交于点E,
∴,,
∵,
∴,
∴是直角三角形,
∴,
∴
.
故答案为:.
13.答案:
解析:如图,作于点D,则,
在中,,
,
在中,,
,
,
即这栋楼的高度为,
故答案为:.
14.答案:
解析:过点G作于点M,过点C作于点N,
则,
∵四边形为菱形,
∴,,,
∴,
∴四边形为矩形,
∴,
在中,,,
∴,
∴,
∵四边形为矩形,
∴,,
∴,
又∵,
∴,
∴,
∴,
∴,
故答案为:.
15.答案:3;30或90
解析:,
,,
;
当点D在线段上时,如图所示:
,
,,,,
,,
,,
;
当点D在射线上时,如图所示:
,
同理可得,,
;
当点D在射线上时,不成立,
综上所述,或,
故答案为:3;30或90.
16.答案:
解析:原式
.
17.答案:(1)14
(2)
解析:(1)在中,,,
,
在中,,
,
;
(2)是边上的中线,
,
,
,
.
18.答案:(1)2
(2)轿车能驶入小区,理由见解析
解析:(1)在中,
∵,,
∴,
∵,
∴,
(2)当时,,则,
在中,
,
∴,
∴,
∴,
∵,
∴轿车能驶入小区.
19.答案:(1)65
(2)4.2米
解析:(1)根据题意,得,
故答案为:65.
(2)过点D作于点F,交于点M,交于点G,
则,
∵四边形为矩形,
∴,,,
∴,
∵,
∴四边形为矩形,
∴,
∵,,
∴,
∴,,
∴,
∴,
∴,
20.答案:6.4米
解析:过点G作,垂足为点H,如图所示:
由题意得:,米,,
设米,
米,
米,
在中,
米
米,
,
,
,
,
,
解得:,
经检验:是原方程的根,
∴(米),
∴塑像的高度为6.4米.
21.答案:(1)点E到地面的高度
(2)点G到直线与交点的距离约为
解析:(1)如图,设EF与GH的交点为点M
,
,即
,
在中,
答:点E到地面的高度;
(2)由(1)已知,
(等腰三角形的三线合一)
,即
则依题意,延长AB分别交GF于点P,交GH于点Q,画图如下所示:
四边形ABCD是矩形
,即
,即
又
四边形BEMQ是平行四边形
平行四边形BEMQ是矩形
,点E是BC的中点
在中,,即
解得
答:点G到直线与交点的距离约为.
