第一章 特殊平行四边形单元质检卷(B卷)九年级上册数学北师大版(2012)(含解析)
文档属性
| 名称 | 第一章 特殊平行四边形单元质检卷(B卷)九年级上册数学北师大版(2012)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-15 22:14:00 | ||
图片预览


文档简介
(2)特殊平行四边形—九年级上册数学北师大版(2012)单元质检卷(B卷)
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.四边形的中点四边形是矩形,那么四边形一定满足条件( )
A.矩形 B.菱形 C.对角线相等 D.对角线互相垂直
2.已知四边形是平行四边形,对角线与交于点O,下列结论不正确的是( )
A.当时,它是菱形 B.当时,它是菱形
C.当时,它是菱形 D.当时,它是菱形
3.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,,F为DE的中点.若的周长为18,则OF的长为( )
A.3 B.4 C. D.
4.如图,菱形的对角线,相交于点O,于点H,连接,若,菱形的面积为,则的长为( )
A.3 B.4 C.5 D.6
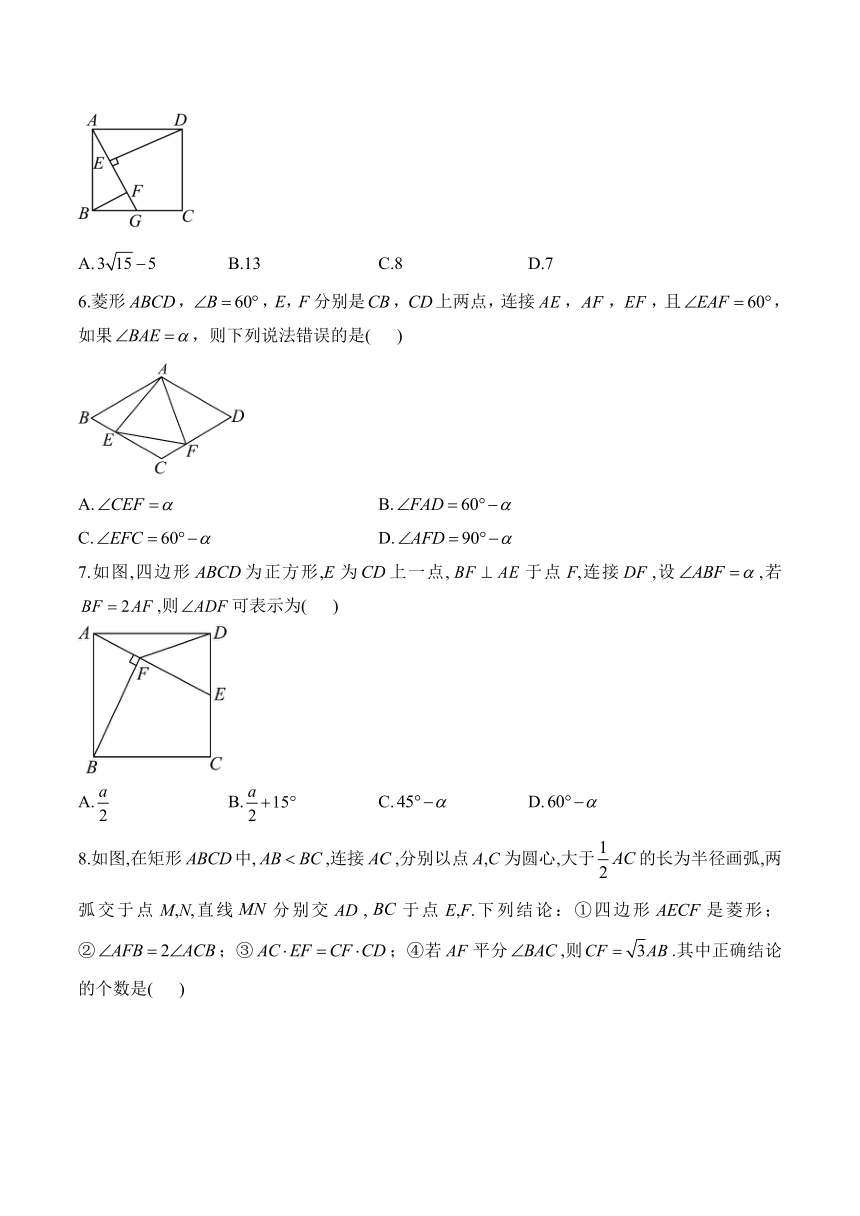
5.如图,正方形ABCD的面积为169,G是BC上的一点,于点E,,且交AG于点F,若,则EF的长是( )
A. B.13 C.8 D.7
6.菱形,,E,F分别是,上两点,连接,,,且,如果,则下列说法错误的是( )
A. B.
C. D.
7.如图,四边形为正方形,E为上一点,于点F,连接,设,若,则可表示为( )
A. B. C. D.
8.如图,在矩形中,,连接,分别以点A,C为圆心,大于的长为半径画弧,两弧交于点M,N,直线分别交,于点E,F.下列结论:①四边形是菱形;②;③;④若平分,则.其中正确结论的个数是( )
A.4 B.3 C.2 D.1
9.如图,在中,,,,为边上一动点,于点E,于点F,点M为的中点,则的最小值为( )
A.1.4 B.2.4 C.1.2 D.1.3
10.如图,菱形ABCD中,,AC与BD交于点O,E为CD延长线上的一点,且,连接BE分别交AC,AD于点F、G,连接OG,则下列结论正确的是( )
①;②与全等的三角形共有2个;③;④由点A、B、D、E构成的四边形是菱形;
A.①③④ B.①④ C.①②③ D.②③④
二、填空题(每小题4分,共20分)
11.已知菱形的面积为,对角线长为,则对角线__________厘米.
12.如图,在矩形中,,,点P为边上任意一点,过点P作,,垂足分别为E、F,则____________.
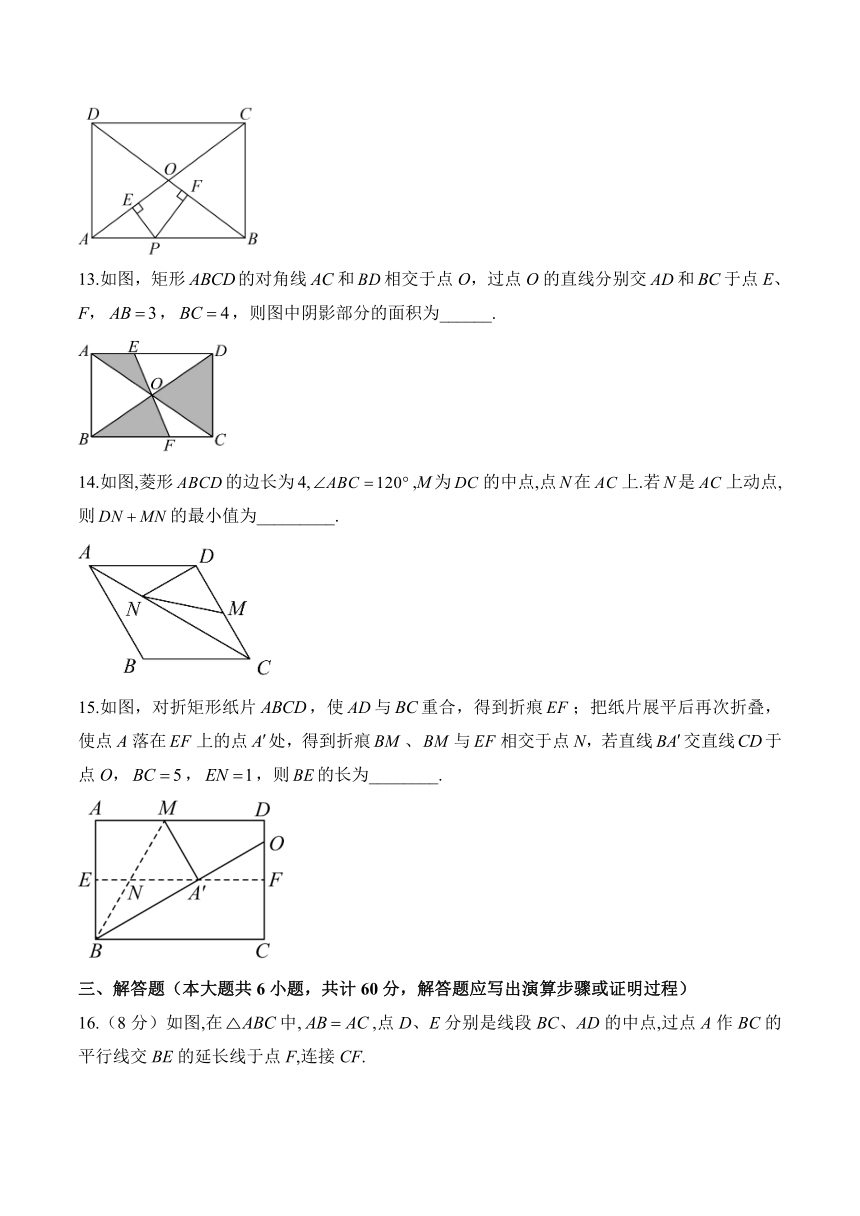
13.如图,矩形的对角线和相交于点O,过点O的直线分别交和于点E、F,,,则图中阴影部分的面积为______.
14.如图,菱形的边长为4,,M为的中点,点N在上.若N是上动点,则的最小值为_________.
15.如图,对折矩形纸片,使与重合,得到折痕;把纸片展平后再次折叠,使点A落在上的点处,得到折痕、与相交于点N,若直线交直线于点O,,,则的长为________.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)如图,在中,,点D、E分别是线段BC、AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:;
(2)求证:四边形ADCF为矩形.
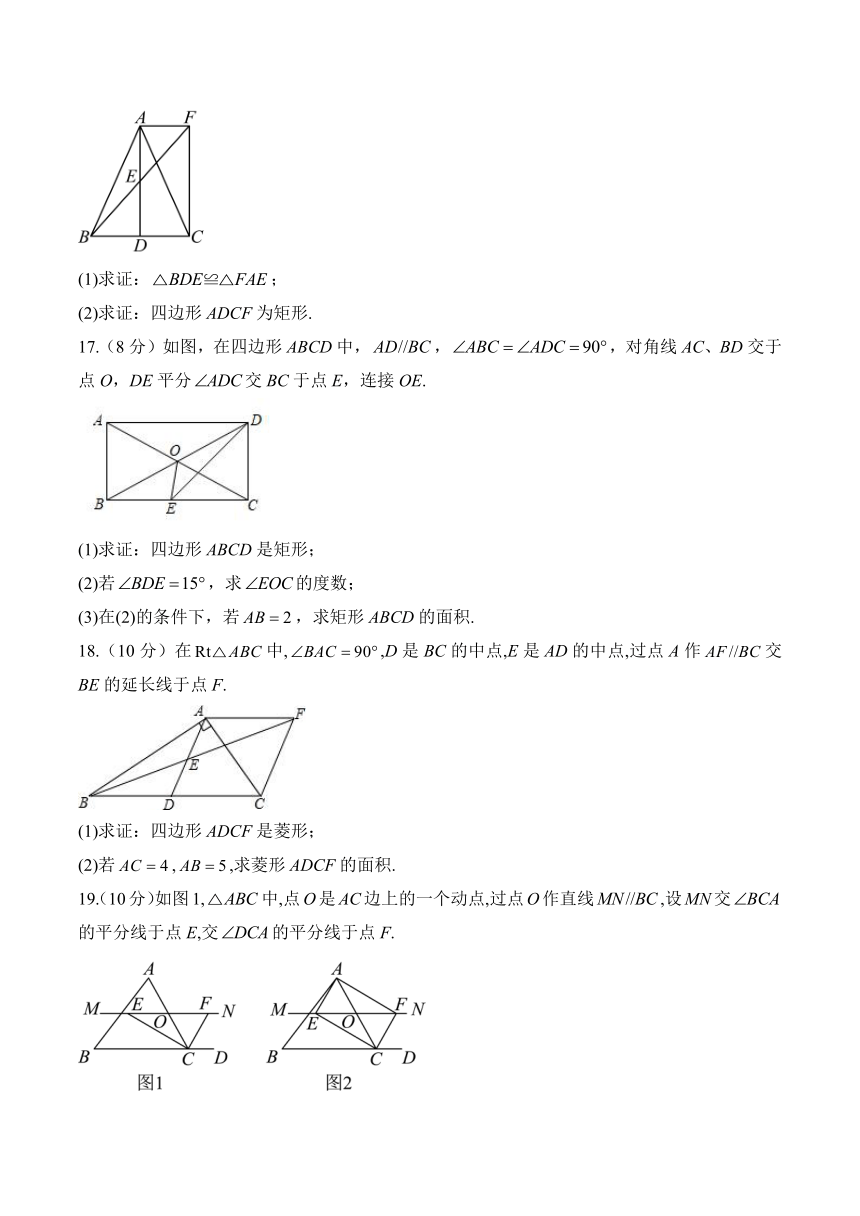
17.(8分)如图,在四边形ABCD中,,,对角线AC、BD交于点O,DE平分交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若,求的度数;
(3)在(2)的条件下,若,求矩形ABCD的面积.
18.(10分)在中,,D是BC的中点,E是AD的中点,过点A作交BE的延长线于点F.
(1)求证:四边形ADCF是菱形;
(2)若,,求菱形ADCF的面积.
19.(10分)如图1,中,点O是AC边上的一个动点,过点O作直线,设MN交的平分线于点E,交的平分线于点F.
(1)线段CE与CF的位置关系是______;
(2)探究:线段OE与OF的数量关系,并加以证明;
(3)如图2,当点O运动到何处时,四边形AECF是矩形,并说明理由;
(4)在(3)的前提下,直接写出满足什么条件时,四边形AECF是正方形.
20.(12分)如图1,正方形中,点E,G,H分别在、、上,且,垂足为点O.
(1)求证:;
(2)平移图1中线段,使点G与点D重合,点H在延长线上,连接,取中点P,连接.如图2,试探究线段CP与BE的数量关系,并说明理由.
21.(12分)我们给出如下定义:有一组邻角相等的凸四边形叫做“等邻角四边形”.例如:如图1,,则四边形为等邻角四边形.
(1)定义以下平面图形中,一定是等邻角四边形的是______;
①平行四边形;②矩形;③菱形;④正方形
(2)如图2,在四边形中,,的垂直平分线恰好交于边上一点P,连接,,且,求证:四边形为等邻角四边形;
(3)如图3,在等邻角四边形中,,,点P为边上的一动点,过点P作,,垂足分别为M,N.在点P的运动过程中,猜想,,之间的数量关系?并请说明理由.
答案以及解析
1.答案:D
解析:四边形的中点四边形是一个矩形,
四边形的对角线一定互相垂直,只要符合此条件即可,
故选:D.
2.答案:D
解析:A、四边形是平行四边形,,
平行四边形是菱形,故选项A不符合题意;
B、四边形是平行四边形,,
平行四边形是菱形,故选项B不符合题意;
C、如图,
四边形是平行四边形,
,
,
,
,
,
平行四边形是菱形,故选项C不符合题意;
D、四边形是平行四边形,,
平行四边形是矩形,故选项D符合题意;
故选:D.
3.答案:D
解析:∵,的周长为18,
∴.
∵F为DE的中点,
∴.
∵,
∴,
∴,
∴,
∴,
∵四边形ABCD是正方形,
∴,O为BD的中点,
∴OF是的中位线,
∴,
故选D.
4.答案:C
解析:四边形ABCD是菱形,
,.
,
.
.
,
.
.
故选:C.
5.答案:D
解析:∵正方形的面积为169,
,
∵于点E,,
∵于点E,,
∴,
∵四边形是正方形,
∴,,
∵,
∴,
在和中,
,
∴,
∴,
∴,
故选:D.
6.答案:D
解析:如图,连接,
四边形是菱形,
,
,
是等边三角形,
,
;
,
,
;
,
,
;
在与中,
,
,
,
,
是等边三角形,
,
,
,
,
故选项A正确;
,
,
,
故选项B正确;
,
故选项C正确;
,
,
故选项D错误;
故选:D.
7.答案:C
解析:如图所示,过点D作于G,
∵四边形是正方形,
∴,,
∵,,
∴,
∴,
∴,
∴,
∴,,,
∵,
∴,
∴,
∴是等腰直角三角形,
∴,
∴,
故选C.
8.答案:C
解析:设交于点O
由作图知,垂直平分
,
在矩形中,
四边形是菱形
∴①正确
四边形是菱形
∴②正确
,
∴③错误
平分
∴④错误.
故选C.
9.答案:C
解析:如图,连接AP
,,,
,
,,
,
∴四边形是矩形,
,
∵M是EF的中点,
,
根据垂线段最短可知,当时,AP最短,
则PM也最短,
此时,
,
,
即AP最短时,,
的最小值,
故选:C.
10.答案:A
解析:∵四边形ABCD是菱形,
∴,,,,,
∴,,
∵,
∴,
在和中,
,
∴,
∴,
∴OG是的中位线,
∴,故①正确;
连接AE,
∵,,
∴四边形ABDE是平行四边形,
∵,
∴、是等边三角形,
∴,,
∴,四边形ABDE是菱形,故④正确;
∴,
由菱形的性质得:,
在和中,
,
∴,
∴,故②不正确;
∵,
∴,
∵四边形ABDE是菱形,
∴,
∴四边形ODEG与四边形OBAG面积相等,故③正确;
故选:A.
11.答案:8
解析:根据菱形的性质可得菱形面积等于对角线相乘除以2,
(厘米),
故答案为:8.
12.答案:
解析:∵矩形中,,,
∴,
∴,,
连接,
根据矩形的性质,得,,
解得,
故答案为:.
13.答案:6
解析:四边形是矩形,
,,,
,
在和中,
,
,
,
,
,
.
故答案为:6
14.答案:
解析:菱形的边长为4,,
,,
是等边三角形,
点关于的对称点为B点,连接交于点N,如图,
∴此时最小,
∵M为的中点,
,,
.
故答案为:.
15.答案:
解析:连接,,
四边形是矩形
由折叠得:,点B与A关于直线对称,点与点A关于直线对称,
垂直平分,垂直平分,
,,,
,
,
,,
,
,
,
,
,,
,
,
,,
,
,
,
,
.
故答案为:.
16.答案:(1)证明见解析
(2)证明见解析
解析:(1)证明:∵,
∴,
∵E是线段AD的中点,
∴,
∵,
∴;
(2)证明:∵,
∴,
∵D是线段BC的中点,
∴,
∴,
∵,
∴四边形ADCF是平行四边形,
∵,
∴,
∴,
∴四边形ADCF为矩形.
17.答案:(1)见解析
(2)75°
(3)
解析:(1)证明:,
,
,
,
,
∴四边形ABCD是矩形;
(2)∵四边形ABCD是矩形,DE平分,
,
,
又,
,
又∵矩形的对角线互相平分且相等,
,
是等边三角形,
,
,
,
;
(3)∵四边形ABCD是矩形,
,,
由(1)可知,,
,
∴,
∴矩形OEC的面积.
18.答案:(1)证明见解析
(2)10
解析:(1)证明:如图,∵,
∴,
∵E是AD的中点,AD是BC边上的中线,
∴,,
在和中,
,
∴;
∴.
∵,
∴,
∴四边形ADCF是平行四边形,
∵,D是BC的中点,
∴,
∴四边形ADCF是菱形;
(2)连接DF,
∵,,
∴四边形ABDF是平行四边形,
∴,
∵四边形ADCF是菱形,
∴.
19.答案:(1)
(2),证明见解析
(3)O运动到AC中点时,四边形AECF是矩形,理由见解析
(4)当时,矩形AECF是正方形
解析:(1)结论:.理由如下:
∵CE平分,CF平分,
∴,,
∵,
∴,
∴,
故答案为:.
(2)结论:.理由如下
∵CE为的平分线,CF为的平分线,
∴,,
∵,
∴,,
∴,,
∴,,
∴.
(3)O运动到AC中点时,四边形AECF是矩形.理由如下:
∵O为中点,
∴,且,
∴四边形AECF平行四边形,
∵,
∴四边形AECF为矩形,
∴当点O运动到AC中点时,四边形AECF为矩形.
(4)当时,矩形AECF是正方形.理由如下:
∵,,
∴,
∴,
∴矩形AECF是正方形.
20.答案:(1)证明见解析
(2),理由见解析
解析:(1)证明:作平行四边形,则,,,
,
,
,
,
在和中,
,
,
;
(2),理由是:
在上截取一点N,使得.则是等腰直角三角形,.
,
,
,,
,
,
,
,即.
21.答案:(1)②④
(2)见解析
(3),理由见解析
解析:(1)∵矩形和正方形都有一组邻角相等,
∴矩形和正方形是等邻角四边形,
故答案是:②④;
(2)证明:连接,
∵垂直平分,
∴,
∵垂直平分,
∴,
在和中
,
∴,
∴,
∴,
∴,
∴四边形为等邻角四边形.
(3),理由如下:
过点P作,垂足为F,
∵,
∴,
∴,
∵四边形为等邻角四边形,,
∴,
∵,
∴,
∴在和中
,
∴,
∴,
∵,,,
∴四边形为矩形,
∴,
∴,
即.
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.四边形的中点四边形是矩形,那么四边形一定满足条件( )
A.矩形 B.菱形 C.对角线相等 D.对角线互相垂直
2.已知四边形是平行四边形,对角线与交于点O,下列结论不正确的是( )
A.当时,它是菱形 B.当时,它是菱形
C.当时,它是菱形 D.当时,它是菱形
3.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,,F为DE的中点.若的周长为18,则OF的长为( )
A.3 B.4 C. D.
4.如图,菱形的对角线,相交于点O,于点H,连接,若,菱形的面积为,则的长为( )
A.3 B.4 C.5 D.6
5.如图,正方形ABCD的面积为169,G是BC上的一点,于点E,,且交AG于点F,若,则EF的长是( )
A. B.13 C.8 D.7
6.菱形,,E,F分别是,上两点,连接,,,且,如果,则下列说法错误的是( )
A. B.
C. D.
7.如图,四边形为正方形,E为上一点,于点F,连接,设,若,则可表示为( )
A. B. C. D.
8.如图,在矩形中,,连接,分别以点A,C为圆心,大于的长为半径画弧,两弧交于点M,N,直线分别交,于点E,F.下列结论:①四边形是菱形;②;③;④若平分,则.其中正确结论的个数是( )
A.4 B.3 C.2 D.1
9.如图,在中,,,,为边上一动点,于点E,于点F,点M为的中点,则的最小值为( )
A.1.4 B.2.4 C.1.2 D.1.3
10.如图,菱形ABCD中,,AC与BD交于点O,E为CD延长线上的一点,且,连接BE分别交AC,AD于点F、G,连接OG,则下列结论正确的是( )
①;②与全等的三角形共有2个;③;④由点A、B、D、E构成的四边形是菱形;
A.①③④ B.①④ C.①②③ D.②③④
二、填空题(每小题4分,共20分)
11.已知菱形的面积为,对角线长为,则对角线__________厘米.
12.如图,在矩形中,,,点P为边上任意一点,过点P作,,垂足分别为E、F,则____________.
13.如图,矩形的对角线和相交于点O,过点O的直线分别交和于点E、F,,,则图中阴影部分的面积为______.
14.如图,菱形的边长为4,,M为的中点,点N在上.若N是上动点,则的最小值为_________.
15.如图,对折矩形纸片,使与重合,得到折痕;把纸片展平后再次折叠,使点A落在上的点处,得到折痕、与相交于点N,若直线交直线于点O,,,则的长为________.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)如图,在中,,点D、E分别是线段BC、AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:;
(2)求证:四边形ADCF为矩形.
17.(8分)如图,在四边形ABCD中,,,对角线AC、BD交于点O,DE平分交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若,求的度数;
(3)在(2)的条件下,若,求矩形ABCD的面积.
18.(10分)在中,,D是BC的中点,E是AD的中点,过点A作交BE的延长线于点F.
(1)求证:四边形ADCF是菱形;
(2)若,,求菱形ADCF的面积.
19.(10分)如图1,中,点O是AC边上的一个动点,过点O作直线,设MN交的平分线于点E,交的平分线于点F.
(1)线段CE与CF的位置关系是______;
(2)探究:线段OE与OF的数量关系,并加以证明;
(3)如图2,当点O运动到何处时,四边形AECF是矩形,并说明理由;
(4)在(3)的前提下,直接写出满足什么条件时,四边形AECF是正方形.
20.(12分)如图1,正方形中,点E,G,H分别在、、上,且,垂足为点O.
(1)求证:;
(2)平移图1中线段,使点G与点D重合,点H在延长线上,连接,取中点P,连接.如图2,试探究线段CP与BE的数量关系,并说明理由.
21.(12分)我们给出如下定义:有一组邻角相等的凸四边形叫做“等邻角四边形”.例如:如图1,,则四边形为等邻角四边形.
(1)定义以下平面图形中,一定是等邻角四边形的是______;
①平行四边形;②矩形;③菱形;④正方形
(2)如图2,在四边形中,,的垂直平分线恰好交于边上一点P,连接,,且,求证:四边形为等邻角四边形;
(3)如图3,在等邻角四边形中,,,点P为边上的一动点,过点P作,,垂足分别为M,N.在点P的运动过程中,猜想,,之间的数量关系?并请说明理由.
答案以及解析
1.答案:D
解析:四边形的中点四边形是一个矩形,
四边形的对角线一定互相垂直,只要符合此条件即可,
故选:D.
2.答案:D
解析:A、四边形是平行四边形,,
平行四边形是菱形,故选项A不符合题意;
B、四边形是平行四边形,,
平行四边形是菱形,故选项B不符合题意;
C、如图,
四边形是平行四边形,
,
,
,
,
,
平行四边形是菱形,故选项C不符合题意;
D、四边形是平行四边形,,
平行四边形是矩形,故选项D符合题意;
故选:D.
3.答案:D
解析:∵,的周长为18,
∴.
∵F为DE的中点,
∴.
∵,
∴,
∴,
∴,
∴,
∵四边形ABCD是正方形,
∴,O为BD的中点,
∴OF是的中位线,
∴,
故选D.
4.答案:C
解析:四边形ABCD是菱形,
,.
,
.
.
,
.
.
故选:C.
5.答案:D
解析:∵正方形的面积为169,
,
∵于点E,,
∵于点E,,
∴,
∵四边形是正方形,
∴,,
∵,
∴,
在和中,
,
∴,
∴,
∴,
故选:D.
6.答案:D
解析:如图,连接,
四边形是菱形,
,
,
是等边三角形,
,
;
,
,
;
,
,
;
在与中,
,
,
,
,
是等边三角形,
,
,
,
,
故选项A正确;
,
,
,
故选项B正确;
,
故选项C正确;
,
,
故选项D错误;
故选:D.
7.答案:C
解析:如图所示,过点D作于G,
∵四边形是正方形,
∴,,
∵,,
∴,
∴,
∴,
∴,
∴,,,
∵,
∴,
∴,
∴是等腰直角三角形,
∴,
∴,
故选C.
8.答案:C
解析:设交于点O
由作图知,垂直平分
,
在矩形中,
四边形是菱形
∴①正确
四边形是菱形
∴②正确
,
∴③错误
平分
∴④错误.
故选C.
9.答案:C
解析:如图,连接AP
,,,
,
,,
,
∴四边形是矩形,
,
∵M是EF的中点,
,
根据垂线段最短可知,当时,AP最短,
则PM也最短,
此时,
,
,
即AP最短时,,
的最小值,
故选:C.
10.答案:A
解析:∵四边形ABCD是菱形,
∴,,,,,
∴,,
∵,
∴,
在和中,
,
∴,
∴,
∴OG是的中位线,
∴,故①正确;
连接AE,
∵,,
∴四边形ABDE是平行四边形,
∵,
∴、是等边三角形,
∴,,
∴,四边形ABDE是菱形,故④正确;
∴,
由菱形的性质得:,
在和中,
,
∴,
∴,故②不正确;
∵,
∴,
∵四边形ABDE是菱形,
∴,
∴四边形ODEG与四边形OBAG面积相等,故③正确;
故选:A.
11.答案:8
解析:根据菱形的性质可得菱形面积等于对角线相乘除以2,
(厘米),
故答案为:8.
12.答案:
解析:∵矩形中,,,
∴,
∴,,
连接,
根据矩形的性质,得,,
解得,
故答案为:.
13.答案:6
解析:四边形是矩形,
,,,
,
在和中,
,
,
,
,
,
.
故答案为:6
14.答案:
解析:菱形的边长为4,,
,,
是等边三角形,
点关于的对称点为B点,连接交于点N,如图,
∴此时最小,
∵M为的中点,
,,
.
故答案为:.
15.答案:
解析:连接,,
四边形是矩形
由折叠得:,点B与A关于直线对称,点与点A关于直线对称,
垂直平分,垂直平分,
,,,
,
,
,,
,
,
,
,
,,
,
,
,,
,
,
,
,
.
故答案为:.
16.答案:(1)证明见解析
(2)证明见解析
解析:(1)证明:∵,
∴,
∵E是线段AD的中点,
∴,
∵,
∴;
(2)证明:∵,
∴,
∵D是线段BC的中点,
∴,
∴,
∵,
∴四边形ADCF是平行四边形,
∵,
∴,
∴,
∴四边形ADCF为矩形.
17.答案:(1)见解析
(2)75°
(3)
解析:(1)证明:,
,
,
,
,
∴四边形ABCD是矩形;
(2)∵四边形ABCD是矩形,DE平分,
,
,
又,
,
又∵矩形的对角线互相平分且相等,
,
是等边三角形,
,
,
,
;
(3)∵四边形ABCD是矩形,
,,
由(1)可知,,
,
∴,
∴矩形OEC的面积.
18.答案:(1)证明见解析
(2)10
解析:(1)证明:如图,∵,
∴,
∵E是AD的中点,AD是BC边上的中线,
∴,,
在和中,
,
∴;
∴.
∵,
∴,
∴四边形ADCF是平行四边形,
∵,D是BC的中点,
∴,
∴四边形ADCF是菱形;
(2)连接DF,
∵,,
∴四边形ABDF是平行四边形,
∴,
∵四边形ADCF是菱形,
∴.
19.答案:(1)
(2),证明见解析
(3)O运动到AC中点时,四边形AECF是矩形,理由见解析
(4)当时,矩形AECF是正方形
解析:(1)结论:.理由如下:
∵CE平分,CF平分,
∴,,
∵,
∴,
∴,
故答案为:.
(2)结论:.理由如下
∵CE为的平分线,CF为的平分线,
∴,,
∵,
∴,,
∴,,
∴,,
∴.
(3)O运动到AC中点时,四边形AECF是矩形.理由如下:
∵O为中点,
∴,且,
∴四边形AECF平行四边形,
∵,
∴四边形AECF为矩形,
∴当点O运动到AC中点时,四边形AECF为矩形.
(4)当时,矩形AECF是正方形.理由如下:
∵,,
∴,
∴,
∴矩形AECF是正方形.
20.答案:(1)证明见解析
(2),理由见解析
解析:(1)证明:作平行四边形,则,,,
,
,
,
,
在和中,
,
,
;
(2),理由是:
在上截取一点N,使得.则是等腰直角三角形,.
,
,
,,
,
,
,
,即.
21.答案:(1)②④
(2)见解析
(3),理由见解析
解析:(1)∵矩形和正方形都有一组邻角相等,
∴矩形和正方形是等邻角四边形,
故答案是:②④;
(2)证明:连接,
∵垂直平分,
∴,
∵垂直平分,
∴,
在和中
,
∴,
∴,
∴,
∴,
∴四边形为等邻角四边形.
(3),理由如下:
过点P作,垂足为F,
∵,
∴,
∴,
∵四边形为等邻角四边形,,
∴,
∵,
∴,
∴在和中
,
∴,
∴,
∵,,,
∴四边形为矩形,
∴,
∴,
即.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
