【预习衔接】第二单元多边形的面积(讲义)-2024-2025学年小学数学五年级上册苏教版
文档属性
| 名称 | 【预习衔接】第二单元多边形的面积(讲义)-2024-2025学年小学数学五年级上册苏教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 254.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-14 00:00:00 | ||
图片预览




文档简介
第二单元多边形的面积
(知识梳理+专项练习)
分数乘法
1.平行四边形的面积 = 底×高 字母公式: S = a h
2.三角形的面积 = 底×高÷2 字母公式: S = a h÷2
3.梯形的面积 = (上底+下底)×高÷2 字母公式: S = (a + b ) h÷2
4、一个平行四边形能分割成两个完全相同的三角形;两个完全相同的三角形能拼成一个平行四边形。
5.一个平行四边形可以分割成两个完全相同的梯形;两个不同的梯形也可能拼成一个平行四边形
6、把一个长方形框拉成平行四边形,周长不变,高变小,面积也变小;同理,把平行四边形框拉成长方形,周长不变,高变大了,面积也变大。
7.把一个平行四边形拼成长方形,面积不变,宽变小了,周长也变小。
7、规则组合图形的面积计算方法:先用分割、拼补的方法,将组合图形转化成已学的简单图形,分别算 出面积;再通过加、减求得。
8、不规则图形的面积估算方法:先数整格的,再数不满整格的,不满整格的除以2折算成整格,最后相加;若不规则图形为轴对称图形,可先算出一半图形的面积,再乘以2。
9、认识公顷和平方千米
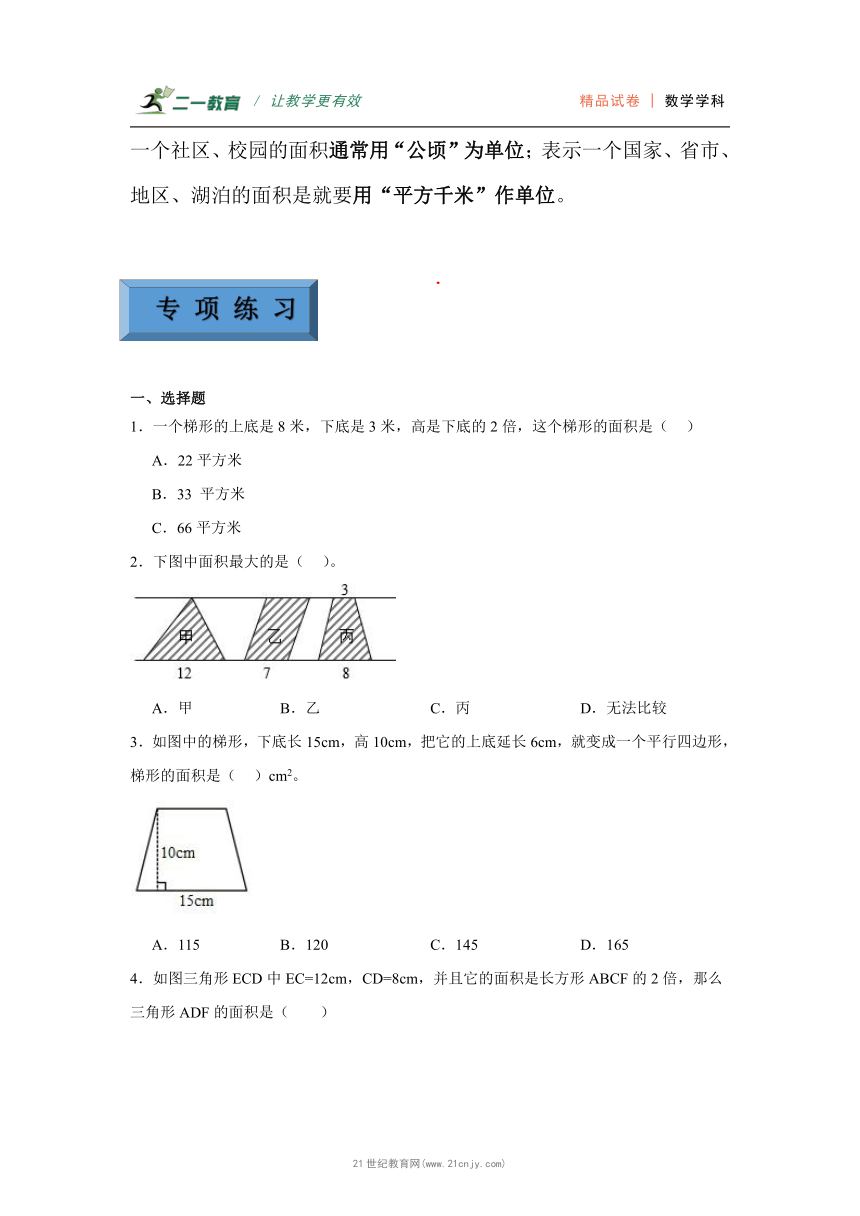
一个社区、校园的面积通常用“公顷”为单位;表示一个国家、省市、地区、湖泊的面积是就要用“平方千米”作单位。
分数乘法
一、选择题
1.一个梯形的上底是8米,下底是3米,高是下底的2倍,这个梯形的面积是( )
A.22平方米
B.33 平方米
C.66平方米
2.下图中面积最大的是( )。
A.甲 B.乙 C.丙 D.无法比较
3.如图中的梯形,下底长15cm,高10cm,把它的上底延长6cm,就变成一个平行四边形,梯形的面积是( )cm2。
A.115 B.120 C.145 D.165
4.如图三角形ECD中EC=12cm,CD=8cm,并且它的面积是长方形ABCF的2倍,那么三角形ADF的面积是( )
A.48平方厘米 B.24平方厘米 C.12平方厘米 D.6平方厘米
5.图中,空白部分的面积是阴影部分面积的( )。
A.一半 B.1倍 C.2倍
6.我国古代数学名著《九章算术》中记载了三角形面积的计算方法是“半广以乘正从”。就是指三角形的面积为( )。
A.底的一半乘高的一半 B.底乘高
C.底的一半乘高 D.底乘高的一半
二、填空题
7.一个平行四边形的相邻两条边分别是6厘米和8厘米,高是7厘米,它的面积( ).
8.第24届冬季奥林匹克运动会于2022年2月4日在北京开幕,2月20日闭幕,从开幕到闭幕共举行了( )天;北京冬季奥林匹克公园在首钢园区的总占地面积为1712000平方米,省略“万”后面的尾数约是( )万平方米,约( )公顷。
9.相同的四个直角三角形的两条直角边分别是12厘米和9厘米,把它们拼成如图所示的正方形,则大正方形的周长是( ) 厘米。
10.在括号里填上“>”“<”或“=”。
489999( )490000 1周角( )2平角
3000公顷( )4平方千米 60000平方米( )6公顷
11.小明家客厅的面积有24( ),客厅的地面爸爸选用了边长是60( )的方砖,国庆节,他们一家参观了占地面积大约是72( )的北京故宫。
12.一个梯形的面积是120平方分米,上底是7分米,下底是13分米,高是( )分米。
13.李大伯用32米长的篱笆一边靠墙,围成了一块菜地(如图),这块菜地的面积是( )平方米。
14.等腰三角形的底是9.6分米,高是4.5分米,等腰三角形的面积是( )平方分米.
15.一个平行四边形的面积是24平方米,那么和它等底等高的三角形的面积是( )平方米;如果三角形的高是4米,则三角形的底是( )米.
16.平行四边形的底是10厘米,高是5厘米,与它等底等高的三角形的面积是( )平方厘米.
17.一个梯形的上底是6dm、下底是8dm,面积是112dm2,这个梯形的高是( )dm.
三、判断题
18.一个梯形的上底是5m,下底是9m,高是8m,这个梯形的面积是180m2. ( )
19.客厅长4.8米,宽3.2米,选用边长6分米的方砖铺地不需要切割。( )
20.两个面积相等的三角形,它们的底和高一定相等。( )
21.面积相等的两个三角形的底和高一定分别相等。( )
22.一个图书馆长为25米,宽为14米,占地面积约为3公顷。( )
23.一张银行卡的面积大约40平方厘米。( )
四、作图题
24.下面每小段的长度表示1厘米。
(1)根据计算面积的公式(3+5)×h÷2,把图形补充完整,并涂上阴影。
(2)再各画一个面积与它相等的平行四边形和三角形。
五、解答题
25.下面方格纸中每个小方格的边长都是1cm。
(1)先在方格纸上画一个底4cm、高3cm的三角形,然后再画一个平行四边形和一个梯形,使得它们的面积都与三角形相等。
(2)上图中,右边不规则图形的面积是( )平方厘米。
一个升旗台的地面如图所示,用边长是0.8m的方砖铺这个升旗台的地面,铺砌它一共需要多少块方砖?(得数保留整数)
27.有一块梯形土地(如图),要划分出一块最大的平行四边形地种黄瓜,该怎样划分?请在图中分一分。剩下的地种卷心菜,如果每棵卷心菜占地9平方分米,一共可以种多少棵卷心菜?
有一块梯形菜地,上底是150米,下底是350米,高是84米,共收白菜25.2吨.这块菜地有多少公顷?平均每公顷收白菜多少吨?
广告公司为某企业制作一块高6米的巨型梯形广告牌,上底6米,下底13米,每平方米收费50元.该企业应付给广告公司多少钱?
广告公司要为一个梯形的广告牌涂一层白色油漆,上底8米,下底12米,高5米.如果每平方米用油漆0.6千克,涂完这个广告牌需要多少千克油漆?
一块三角形菜地面积是3600平方米,底80米,菜地三角形的高是多少米?
在如图中,平行四边形的面积是20平方厘米,阴影部分的面积是多少平方厘米?
33.一批同样的圆木堆在一起的横截面是一个梯形,上层是5根,下层是10根,一共6层,这批圆木共有多少根?
/ 让教学更有效 精品试卷 | 数学学科
/ 让教学更有效 精品试卷 | 数学学科
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【分析】先用3×2求出高,然后根据梯形面积=(上底+下底)×高÷2即可解答。
【详解】(8+3)×3×2÷2
=11×3×2÷2
=33(平方米)
故答案为:B
【点睛】此题主要考查学生对梯形面积的理解与实际应用。
2.B
【分析】设三个图形的高都是h,根据“三角形的面积=底×高÷2”求出三角形的面积;根据“平行四边形的面积=底×高”求出平行四边形的面积;根据“梯形的面积=(上底+下底)×高÷2”求出梯形的面积;进而比较即可得出结论。
【详解】解:设三个图形的高都是h,则:
三角形的面积:12h÷2=6h
平行四边形的面积:7h
梯形的面积:
(3+8)h÷2
=11h÷2
=5.5h
7h>6h>5.5h
所以平行四边形的面积最大。
故答案为:B
【点睛】此题应根据三角形、平行四边形和梯形的面积计算公式进行分析、解答。
3.B
【分析】根据题意可知,上底比下底短6厘米,根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。
【详解】(15-6+15)×10÷2
=24×10÷2
=240÷2
=120(cm2)
故答案为:B
【点睛】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
4.C
【分析】根据三角形的面积公式S=ab÷2,求出三角形ECD的面积,进而求出长方形ABCF的面积;从图中知道三角形ADF的面积是长方形ABCF面积的一半,由此解决问题.
【详解】三角形ECD的面积:12×8÷2=48(平方厘米),
长方形ABCF的面积:48÷2=24(平方厘米),
三角形ADF的面积是:24÷2=12(平方厘米),
答:三角形ADF的面积是12平方厘米;
故选C.
5.C
【详解】大的图形是梯形,分成了3个小三角形,中间的阴影部分三角形与左右的空白三角形都是等底等高的三角形,故面积都相等.所以空白部分的三角形的面积是阴影部分三角形面积的2倍.由图可知,空白部分的面积是阴影部分面积的2倍。
故答案为:C
6.C
【分析】“半广以乘正从”,“广是指三角形的底边,正从是指底边上的高。整句话的意思是:三角形的面积等于底的一半乘高,据此解答。
【详解】2000多年前,我国的数学名著《九章算术》中记载三角形面积的计算方法是“半广以乘正从”,“从”指的是指底边上的高,三角形的面积等于底的一半乘高。
故选:C
【点睛】本题主要考查了学生对历史上三角形的面积计算的研究有关的知识,多了解历史上的数学是解题关键。
7.42平方厘米
【解析】略
8. 17 171 171
【分析】由题可知,用20减4加1就是冬奥会共历时的天数;根据省略“万”后面的尾数的方法,1712000的万位后面一位上是2,不满5舍掉,并在万位后面加上“万”字;根据平方米与公顷间的进率,1公顷=10000平方米,大化小乘进率,小化大除以进率,据此计算即可。
【详解】(1)20-4+1=17(天)
(2)1712000≈171万
(3)1712000≈1710000
1710000÷10000=171
1712000平方米≈171公顷
【点睛】本题主要考查了日期和时间的推算、以及多位数省略“万”位后面的尾数。
9.60
【分析】中间小正方形的边长为12-9=3厘米,面积等于3×3=9平方厘米,一个直角三角形的面积为12×9÷2=54平方厘米,乘4等于4个直角三角形的面积,再加上中间小正方形的面积即等于大正方形的面积,再根据面积等于边长乘边长即可求出大正方形的边长,再乘4即等于正方形的周长。
【详解】12-9=3(厘米)
3×3=9(平方厘米)
12×9÷2×4
=108÷2×4
=54×4
=216(平方厘米)
216+9=225(平方厘米)
225=15×15,所以正方形的边长是:15厘米,
15×4=60(厘米)
【点睛】本题主要考查学生对三角形、正方形面积公式的灵活运用。
10. < = > =
【分析】(1)整数比较大小时,要看他们的数位。数位多的那个数就大;如果数位相同,就看最高位,最高位上的数大,那个数就大;最高位上的数相同,就看下一位,哪一位上的数大,那个数就大。
(2)周角为360°,平角为180°,据此可知2平角=360°=1周角。
(3)公顷和平方千米之间的进率是100,平方米和公顷之间的进率是10000,据此将各个数统一单位,再比较大小。
【详解】489999<490000
1周角=2平角
3000公顷=30平方千米,30平方千米>4平方千米,则3000公顷>4平方千米
60000平方米=6公顷
【点睛】整数比较大小时,从高位起,依次比较相同数位上的数。不同单位的数比较大小,先换算成同一单位的数,再比较大小。
11. 平方米 厘米 公顷
【分析】根据生活经验、对面积单位、长度单位和数据大小的认识:
计量小明家客厅的面积,结合数据24可知:应用“平方米”做单位;
计量客厅地面的方砖边长,结合数据60可知:应用“厘米”做单位;
计量北京故宫占地面积,结合数据72可知:应用“公顷”做单位。
【详解】小明家客厅的面积有24平方米,客厅的地面爸爸选用了边长是60厘米的方砖,国庆节,他们一家参观了占地面积大约是72公顷的北京故宫。
【点睛】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活的选择。
12.12
【分析】根据梯形的面积公式:梯形面积=(上底+下底)×高÷2;高=梯形面积×2÷(上底+下底),代入数据,即可解答。
【详解】120×2÷(7+13)
=240÷20
=12(分米)
【点睛】本题考查梯形面积公式的应用,关键是熟记公式,灵活运用。
13.120
【分析】由题意可知:梯形的上、下底之和是32-12=20米,带入梯形的面积公式计算即可。
【详解】(32-12)×12÷2
=20×12÷2
=120(平方米)
【点睛】本题主要考查梯形面积公式的灵活应用,牢记公式是解题的关键。
14.21.6
【解析】略
15.12,6
【详解】试题分析:如果三角形和平行四边形等底等高,那么三角形的面积是平行四边形面积的一半;根据三角形的底=面积×2÷高,即可得答案.
解:24÷2=12(平方厘米);
12×2÷4=6(厘米);
答:和它等底等高的三角形的面积是12平方厘米;三角形的底是6米.
点评:此题主要考查等底等高的三角形和平行四边形面积之间的关系,及三角形的面积公式.
16.25
【详解】略
17.16
【详解】根据梯形的面积=(上底+下底)×高÷2,已知梯形的面积和上底、下底,求梯形的高,用梯形的面积×2÷(上底+下底)=梯形的高
18.错误
【详解】(5+9)×8÷2
=14×8÷2
=112÷2
=56(m2)
原题说法错误.
19.×
【分析】根据题意分析,用客厅的长和宽分别除以6分米,如果商都为整数则方砖不需要切割,只要其中有一个不为整数,那么方砖就需要切割,据此判断。
【详解】4.8米=48×10=48分米
3.2米=3.2×10=32分米
48÷6=8(个)
32÷6=5(个)…2(分米)
因为32不是6的整数倍,所以选用边长6分米的方砖铺地需要切割,原题干说法错误。
故答案为:×
20.×
【分析】根据“三角形的面积=底×高÷2”可知,三角形的面积是由底和高决定的,当两个三角形的底和高不相等时,底和高的乘积可能相等;可以举例说明。
【详解】如:一个三角形的底是6cm、高是2cm;另一个三角形的底是4cm、高是3cm;
6×2÷2=6(cm2)
4×3÷2=6(cm2)
两个面积都是6cm2的三角形,它们的底和高不相等。
所以,两个面积相等的三角形,它们的底和高不一定相等。
原题说法错误。
故答案为:×
21.×
【分析】三角形面积=底×高÷2,面积相等的两个三角形,只能说它们底和高的乘积是相等的但两个三角形的底和高不一定相等。
【详解】如:一个三角形的底为6,高为2,它的面积是6×2÷2=6;
另一个三角形的底为4,高为3,它的面积是4×3÷2=6。此时这两个三角形的面积相等,但底和高都不相等。所以原题说法错误。
故答案为:×
【点睛】本题考查三角形的面积,明确三角形的底和高的乘积相等,则三角形的面积一定相等,但形状可能不同是解题的关键。
22.×
【分析】根据长方形面积=长×宽,代入数据求出图书馆的占地面积,再将面积单位转化为公顷,最后与题干比较即可。
【详解】25×14=350(平方米)
350平方米=0.035公顷
0.035公顷≠3公顷
故答案为:×
【点睛】本题主要考查公顷与平方米的转化,解题时要明确低级单位转化为高级单位要除以进率。
23.√
【分析】根据生活经验、对面积单位和数据大小的认识,可知计量一张银行卡的面积用“平方厘米”作单位,且一张银行卡的面积大约40平方厘米。
【详解】一张银行卡的面积大约40平方厘米。
故答案为:√
【点睛】根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活地选择。
24.(1)(2)见详解
【分析】(1)根据计算面积的公式(3+5)×h÷2,观察算式,是利用了梯形的面积公式,把3看作梯形的上底,5看作梯形的下底,所以在图形中,补充画一个上底为3厘米,下底为5厘米的梯形即可,并涂上阴影。
(2)计算面积(3+5)×h÷2=4h,要画一个面积与它相等的平行四边形和三角形,分别利用平行四边形和三角形的面积公式,可画一个底为4厘米,高为h厘米的平行四边形和画一个底为8厘米,高为h厘米的三角形即可满足题意。
【详解】(1)如图:
(2)(3+5)×h÷2
=8×h÷2
=4h(平方厘米)
4h÷h=4(厘米)
所以平行四边形的底边长为4厘米;
4h×2÷h=8(厘米)
所以三角形的底边长为8厘米。
如图:
【点睛】此题的解题关键是灵活运用平行四边形、梯形、三角形的面积公式,画出指定面积的图形。
25.(1)见详解(答案不唯一);(2)5.5
【分析】(1)因为三角形的底是4厘米,高是3厘米,那么运用三角形的面积公式:底×高÷2算出三角形的面积即4×3÷2=6(平方厘米),因为要画一个平行四边形和梯形,它们的面积跟三角形的相等,即可求出平行四边形的下底是6÷4=1.5(厘米),梯形的上底加下底的和是:6×2÷3=4(厘米),画出图即可(答案不唯一);
(2)把这个不规则图形分成两部分,上半部分是个三角形,运用三角形的面积公式即可求出三角形的面积是多少;下半部分是一个梯形,上底是4厘米,下底是3厘米,高是1厘米根据梯形的面积公式:梯形的面积=(上底+下底)×高÷2,再加上上半部分三角形的面积即可。
【详解】(1)
(2)4×1÷2+(4+3)×1÷2
=2+3.5
=5.5(平方厘米)
【点睛】本题主要考查平行四边形,三角形,梯形的面积公式,熟练掌握它们的面积公式并灵活运用即可。
26.113块
【详解】试题分析:首先根据梯形的面积公式:s=(a+b)×2,求出升旗台的面积,再根据正方形的面积公式:s=a2,求出每块方砖的面积,然后升旗台的面积除以每块方砖的面积.据此列式解答.
解:(6+12)×8÷2÷(0.8×0.8),
=18×8÷2÷0.64,
=72÷0.64,
≈113(块);
答:铺砌它一共需要113块方砖.
点评:此题主要考查梯形、正方形面积公式的灵活应用.
27.见详解(画法不唯一);1000棵
【分析】从梯形中分出一个最大的平行四边形,则以梯形较短的底和一条腰作为平行四边形相邻的两条边即可;根据梯形的面积=(上底+下底)×高÷2,平行四边形的面积=底×高,求出剩余的面积,根据1平方米=100平方分米,高级单位转化成低级单位乘进率,换算后再除以9即可求解。
【详解】如图:
(35+26)×20÷2
=61×20÷2
=1220÷2
=610(平方米)
26×20=520(平方米)
610-520=90(平方米)
90平方米=9000平方分米
9000÷9=1000(棵)
答:一共可以种1000棵卷心菜。
【点睛】本题考查梯形和平行四边形的面积公式,要重点掌握。
28.12吨
【详解】试题分析:根据题意,可利用梯形的面积公式(上底+下底)×高÷2计算出这块梯形菜地的面积,然后再用25.2吨白菜除以菜地的面积即可得到答案.
解:菜地的面积为:(150+350)×84÷2
=500×84÷2,
=42000÷2,
=21000(平方米),
21000平方米=2.1公顷,
25.2÷2.1=12(吨),
答:平均每公顷收白菜12吨.
点评:解答此题的关键是确定梯形菜地的面积.
29.2850元
【详解】(6+13)×6÷2×50=2850(元)
30.30千克
【详解】试题分析:此题实际上是求这块梯形广告牌的面积,梯形的上底、下底和高已知,则面积可求;每平方米的用漆量已知,从而能求出总的用漆量.
解:(8+12)×5÷2×0.6,
=20×5÷2×0.6,
=100÷2×0.6,
=50×0.6,
=30(千克);
答:这块广告牌需要30千克油漆.
点评:解答此题的关键是明白:先求出这块梯形广告牌的面积,进而可以求出总的用漆量.
31.90米
【详解】3600×2÷80
=7200÷80
=90(米)
答:菜地三角形的高是90米.
32.4平方厘米
【详解】试题分析:首先我用字母标出各点,从图上可知阴影部分的面积是一个三角形,又知一个底AE的长度是2厘米,只要再求出高来就可以了,又知平行四边形的面积是20平方厘米,其中一底边为2+3=5厘米,再根据求出高来,也就是阴影部分 三角形的高,最后利用三角形的面积公式求出即可.
已知平行四边形的面积是20平方厘米,其中一底边为2+3=5厘米,设高EF为X厘米,
S平行四边形=AD×X,
5X=20,
X=4,
所以,S△ACE=×AE×EF=×2×4=4(平方厘米).
答:阴影部分的面积是4平方厘米.
点评:此题重在根据三角形的面积公式和平行四边形的面积公式的灵活运用.
33.45根
【详解】试题分析:梯形的面积=(上底+下底)×高÷2,将数据代入公式即可求解.
解:(5+10)×6÷2,
=15×6÷2,
=45(根);
答:这批圆木共有45根.
点评:此题主要考查梯形的面积的计算方法在实际生活中的应用.
答案第1页,共2页
答案第1页,共2页
(知识梳理+专项练习)
分数乘法
1.平行四边形的面积 = 底×高 字母公式: S = a h
2.三角形的面积 = 底×高÷2 字母公式: S = a h÷2
3.梯形的面积 = (上底+下底)×高÷2 字母公式: S = (a + b ) h÷2
4、一个平行四边形能分割成两个完全相同的三角形;两个完全相同的三角形能拼成一个平行四边形。
5.一个平行四边形可以分割成两个完全相同的梯形;两个不同的梯形也可能拼成一个平行四边形
6、把一个长方形框拉成平行四边形,周长不变,高变小,面积也变小;同理,把平行四边形框拉成长方形,周长不变,高变大了,面积也变大。
7.把一个平行四边形拼成长方形,面积不变,宽变小了,周长也变小。
7、规则组合图形的面积计算方法:先用分割、拼补的方法,将组合图形转化成已学的简单图形,分别算 出面积;再通过加、减求得。
8、不规则图形的面积估算方法:先数整格的,再数不满整格的,不满整格的除以2折算成整格,最后相加;若不规则图形为轴对称图形,可先算出一半图形的面积,再乘以2。
9、认识公顷和平方千米
一个社区、校园的面积通常用“公顷”为单位;表示一个国家、省市、地区、湖泊的面积是就要用“平方千米”作单位。
分数乘法
一、选择题
1.一个梯形的上底是8米,下底是3米,高是下底的2倍,这个梯形的面积是( )
A.22平方米
B.33 平方米
C.66平方米
2.下图中面积最大的是( )。
A.甲 B.乙 C.丙 D.无法比较
3.如图中的梯形,下底长15cm,高10cm,把它的上底延长6cm,就变成一个平行四边形,梯形的面积是( )cm2。
A.115 B.120 C.145 D.165
4.如图三角形ECD中EC=12cm,CD=8cm,并且它的面积是长方形ABCF的2倍,那么三角形ADF的面积是( )
A.48平方厘米 B.24平方厘米 C.12平方厘米 D.6平方厘米
5.图中,空白部分的面积是阴影部分面积的( )。
A.一半 B.1倍 C.2倍
6.我国古代数学名著《九章算术》中记载了三角形面积的计算方法是“半广以乘正从”。就是指三角形的面积为( )。
A.底的一半乘高的一半 B.底乘高
C.底的一半乘高 D.底乘高的一半
二、填空题
7.一个平行四边形的相邻两条边分别是6厘米和8厘米,高是7厘米,它的面积( ).
8.第24届冬季奥林匹克运动会于2022年2月4日在北京开幕,2月20日闭幕,从开幕到闭幕共举行了( )天;北京冬季奥林匹克公园在首钢园区的总占地面积为1712000平方米,省略“万”后面的尾数约是( )万平方米,约( )公顷。
9.相同的四个直角三角形的两条直角边分别是12厘米和9厘米,把它们拼成如图所示的正方形,则大正方形的周长是( ) 厘米。
10.在括号里填上“>”“<”或“=”。
489999( )490000 1周角( )2平角
3000公顷( )4平方千米 60000平方米( )6公顷
11.小明家客厅的面积有24( ),客厅的地面爸爸选用了边长是60( )的方砖,国庆节,他们一家参观了占地面积大约是72( )的北京故宫。
12.一个梯形的面积是120平方分米,上底是7分米,下底是13分米,高是( )分米。
13.李大伯用32米长的篱笆一边靠墙,围成了一块菜地(如图),这块菜地的面积是( )平方米。
14.等腰三角形的底是9.6分米,高是4.5分米,等腰三角形的面积是( )平方分米.
15.一个平行四边形的面积是24平方米,那么和它等底等高的三角形的面积是( )平方米;如果三角形的高是4米,则三角形的底是( )米.
16.平行四边形的底是10厘米,高是5厘米,与它等底等高的三角形的面积是( )平方厘米.
17.一个梯形的上底是6dm、下底是8dm,面积是112dm2,这个梯形的高是( )dm.
三、判断题
18.一个梯形的上底是5m,下底是9m,高是8m,这个梯形的面积是180m2. ( )
19.客厅长4.8米,宽3.2米,选用边长6分米的方砖铺地不需要切割。( )
20.两个面积相等的三角形,它们的底和高一定相等。( )
21.面积相等的两个三角形的底和高一定分别相等。( )
22.一个图书馆长为25米,宽为14米,占地面积约为3公顷。( )
23.一张银行卡的面积大约40平方厘米。( )
四、作图题
24.下面每小段的长度表示1厘米。
(1)根据计算面积的公式(3+5)×h÷2,把图形补充完整,并涂上阴影。
(2)再各画一个面积与它相等的平行四边形和三角形。
五、解答题
25.下面方格纸中每个小方格的边长都是1cm。
(1)先在方格纸上画一个底4cm、高3cm的三角形,然后再画一个平行四边形和一个梯形,使得它们的面积都与三角形相等。
(2)上图中,右边不规则图形的面积是( )平方厘米。
一个升旗台的地面如图所示,用边长是0.8m的方砖铺这个升旗台的地面,铺砌它一共需要多少块方砖?(得数保留整数)
27.有一块梯形土地(如图),要划分出一块最大的平行四边形地种黄瓜,该怎样划分?请在图中分一分。剩下的地种卷心菜,如果每棵卷心菜占地9平方分米,一共可以种多少棵卷心菜?
有一块梯形菜地,上底是150米,下底是350米,高是84米,共收白菜25.2吨.这块菜地有多少公顷?平均每公顷收白菜多少吨?
广告公司为某企业制作一块高6米的巨型梯形广告牌,上底6米,下底13米,每平方米收费50元.该企业应付给广告公司多少钱?
广告公司要为一个梯形的广告牌涂一层白色油漆,上底8米,下底12米,高5米.如果每平方米用油漆0.6千克,涂完这个广告牌需要多少千克油漆?
一块三角形菜地面积是3600平方米,底80米,菜地三角形的高是多少米?
在如图中,平行四边形的面积是20平方厘米,阴影部分的面积是多少平方厘米?
33.一批同样的圆木堆在一起的横截面是一个梯形,上层是5根,下层是10根,一共6层,这批圆木共有多少根?
/ 让教学更有效 精品试卷 | 数学学科
/ 让教学更有效 精品试卷 | 数学学科
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【分析】先用3×2求出高,然后根据梯形面积=(上底+下底)×高÷2即可解答。
【详解】(8+3)×3×2÷2
=11×3×2÷2
=33(平方米)
故答案为:B
【点睛】此题主要考查学生对梯形面积的理解与实际应用。
2.B
【分析】设三个图形的高都是h,根据“三角形的面积=底×高÷2”求出三角形的面积;根据“平行四边形的面积=底×高”求出平行四边形的面积;根据“梯形的面积=(上底+下底)×高÷2”求出梯形的面积;进而比较即可得出结论。
【详解】解:设三个图形的高都是h,则:
三角形的面积:12h÷2=6h
平行四边形的面积:7h
梯形的面积:
(3+8)h÷2
=11h÷2
=5.5h
7h>6h>5.5h
所以平行四边形的面积最大。
故答案为:B
【点睛】此题应根据三角形、平行四边形和梯形的面积计算公式进行分析、解答。
3.B
【分析】根据题意可知,上底比下底短6厘米,根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。
【详解】(15-6+15)×10÷2
=24×10÷2
=240÷2
=120(cm2)
故答案为:B
【点睛】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
4.C
【分析】根据三角形的面积公式S=ab÷2,求出三角形ECD的面积,进而求出长方形ABCF的面积;从图中知道三角形ADF的面积是长方形ABCF面积的一半,由此解决问题.
【详解】三角形ECD的面积:12×8÷2=48(平方厘米),
长方形ABCF的面积:48÷2=24(平方厘米),
三角形ADF的面积是:24÷2=12(平方厘米),
答:三角形ADF的面积是12平方厘米;
故选C.
5.C
【详解】大的图形是梯形,分成了3个小三角形,中间的阴影部分三角形与左右的空白三角形都是等底等高的三角形,故面积都相等.所以空白部分的三角形的面积是阴影部分三角形面积的2倍.由图可知,空白部分的面积是阴影部分面积的2倍。
故答案为:C
6.C
【分析】“半广以乘正从”,“广是指三角形的底边,正从是指底边上的高。整句话的意思是:三角形的面积等于底的一半乘高,据此解答。
【详解】2000多年前,我国的数学名著《九章算术》中记载三角形面积的计算方法是“半广以乘正从”,“从”指的是指底边上的高,三角形的面积等于底的一半乘高。
故选:C
【点睛】本题主要考查了学生对历史上三角形的面积计算的研究有关的知识,多了解历史上的数学是解题关键。
7.42平方厘米
【解析】略
8. 17 171 171
【分析】由题可知,用20减4加1就是冬奥会共历时的天数;根据省略“万”后面的尾数的方法,1712000的万位后面一位上是2,不满5舍掉,并在万位后面加上“万”字;根据平方米与公顷间的进率,1公顷=10000平方米,大化小乘进率,小化大除以进率,据此计算即可。
【详解】(1)20-4+1=17(天)
(2)1712000≈171万
(3)1712000≈1710000
1710000÷10000=171
1712000平方米≈171公顷
【点睛】本题主要考查了日期和时间的推算、以及多位数省略“万”位后面的尾数。
9.60
【分析】中间小正方形的边长为12-9=3厘米,面积等于3×3=9平方厘米,一个直角三角形的面积为12×9÷2=54平方厘米,乘4等于4个直角三角形的面积,再加上中间小正方形的面积即等于大正方形的面积,再根据面积等于边长乘边长即可求出大正方形的边长,再乘4即等于正方形的周长。
【详解】12-9=3(厘米)
3×3=9(平方厘米)
12×9÷2×4
=108÷2×4
=54×4
=216(平方厘米)
216+9=225(平方厘米)
225=15×15,所以正方形的边长是:15厘米,
15×4=60(厘米)
【点睛】本题主要考查学生对三角形、正方形面积公式的灵活运用。
10. < = > =
【分析】(1)整数比较大小时,要看他们的数位。数位多的那个数就大;如果数位相同,就看最高位,最高位上的数大,那个数就大;最高位上的数相同,就看下一位,哪一位上的数大,那个数就大。
(2)周角为360°,平角为180°,据此可知2平角=360°=1周角。
(3)公顷和平方千米之间的进率是100,平方米和公顷之间的进率是10000,据此将各个数统一单位,再比较大小。
【详解】489999<490000
1周角=2平角
3000公顷=30平方千米,30平方千米>4平方千米,则3000公顷>4平方千米
60000平方米=6公顷
【点睛】整数比较大小时,从高位起,依次比较相同数位上的数。不同单位的数比较大小,先换算成同一单位的数,再比较大小。
11. 平方米 厘米 公顷
【分析】根据生活经验、对面积单位、长度单位和数据大小的认识:
计量小明家客厅的面积,结合数据24可知:应用“平方米”做单位;
计量客厅地面的方砖边长,结合数据60可知:应用“厘米”做单位;
计量北京故宫占地面积,结合数据72可知:应用“公顷”做单位。
【详解】小明家客厅的面积有24平方米,客厅的地面爸爸选用了边长是60厘米的方砖,国庆节,他们一家参观了占地面积大约是72公顷的北京故宫。
【点睛】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活的选择。
12.12
【分析】根据梯形的面积公式:梯形面积=(上底+下底)×高÷2;高=梯形面积×2÷(上底+下底),代入数据,即可解答。
【详解】120×2÷(7+13)
=240÷20
=12(分米)
【点睛】本题考查梯形面积公式的应用,关键是熟记公式,灵活运用。
13.120
【分析】由题意可知:梯形的上、下底之和是32-12=20米,带入梯形的面积公式计算即可。
【详解】(32-12)×12÷2
=20×12÷2
=120(平方米)
【点睛】本题主要考查梯形面积公式的灵活应用,牢记公式是解题的关键。
14.21.6
【解析】略
15.12,6
【详解】试题分析:如果三角形和平行四边形等底等高,那么三角形的面积是平行四边形面积的一半;根据三角形的底=面积×2÷高,即可得答案.
解:24÷2=12(平方厘米);
12×2÷4=6(厘米);
答:和它等底等高的三角形的面积是12平方厘米;三角形的底是6米.
点评:此题主要考查等底等高的三角形和平行四边形面积之间的关系,及三角形的面积公式.
16.25
【详解】略
17.16
【详解】根据梯形的面积=(上底+下底)×高÷2,已知梯形的面积和上底、下底,求梯形的高,用梯形的面积×2÷(上底+下底)=梯形的高
18.错误
【详解】(5+9)×8÷2
=14×8÷2
=112÷2
=56(m2)
原题说法错误.
19.×
【分析】根据题意分析,用客厅的长和宽分别除以6分米,如果商都为整数则方砖不需要切割,只要其中有一个不为整数,那么方砖就需要切割,据此判断。
【详解】4.8米=48×10=48分米
3.2米=3.2×10=32分米
48÷6=8(个)
32÷6=5(个)…2(分米)
因为32不是6的整数倍,所以选用边长6分米的方砖铺地需要切割,原题干说法错误。
故答案为:×
20.×
【分析】根据“三角形的面积=底×高÷2”可知,三角形的面积是由底和高决定的,当两个三角形的底和高不相等时,底和高的乘积可能相等;可以举例说明。
【详解】如:一个三角形的底是6cm、高是2cm;另一个三角形的底是4cm、高是3cm;
6×2÷2=6(cm2)
4×3÷2=6(cm2)
两个面积都是6cm2的三角形,它们的底和高不相等。
所以,两个面积相等的三角形,它们的底和高不一定相等。
原题说法错误。
故答案为:×
21.×
【分析】三角形面积=底×高÷2,面积相等的两个三角形,只能说它们底和高的乘积是相等的但两个三角形的底和高不一定相等。
【详解】如:一个三角形的底为6,高为2,它的面积是6×2÷2=6;
另一个三角形的底为4,高为3,它的面积是4×3÷2=6。此时这两个三角形的面积相等,但底和高都不相等。所以原题说法错误。
故答案为:×
【点睛】本题考查三角形的面积,明确三角形的底和高的乘积相等,则三角形的面积一定相等,但形状可能不同是解题的关键。
22.×
【分析】根据长方形面积=长×宽,代入数据求出图书馆的占地面积,再将面积单位转化为公顷,最后与题干比较即可。
【详解】25×14=350(平方米)
350平方米=0.035公顷
0.035公顷≠3公顷
故答案为:×
【点睛】本题主要考查公顷与平方米的转化,解题时要明确低级单位转化为高级单位要除以进率。
23.√
【分析】根据生活经验、对面积单位和数据大小的认识,可知计量一张银行卡的面积用“平方厘米”作单位,且一张银行卡的面积大约40平方厘米。
【详解】一张银行卡的面积大约40平方厘米。
故答案为:√
【点睛】根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活地选择。
24.(1)(2)见详解
【分析】(1)根据计算面积的公式(3+5)×h÷2,观察算式,是利用了梯形的面积公式,把3看作梯形的上底,5看作梯形的下底,所以在图形中,补充画一个上底为3厘米,下底为5厘米的梯形即可,并涂上阴影。
(2)计算面积(3+5)×h÷2=4h,要画一个面积与它相等的平行四边形和三角形,分别利用平行四边形和三角形的面积公式,可画一个底为4厘米,高为h厘米的平行四边形和画一个底为8厘米,高为h厘米的三角形即可满足题意。
【详解】(1)如图:
(2)(3+5)×h÷2
=8×h÷2
=4h(平方厘米)
4h÷h=4(厘米)
所以平行四边形的底边长为4厘米;
4h×2÷h=8(厘米)
所以三角形的底边长为8厘米。
如图:
【点睛】此题的解题关键是灵活运用平行四边形、梯形、三角形的面积公式,画出指定面积的图形。
25.(1)见详解(答案不唯一);(2)5.5
【分析】(1)因为三角形的底是4厘米,高是3厘米,那么运用三角形的面积公式:底×高÷2算出三角形的面积即4×3÷2=6(平方厘米),因为要画一个平行四边形和梯形,它们的面积跟三角形的相等,即可求出平行四边形的下底是6÷4=1.5(厘米),梯形的上底加下底的和是:6×2÷3=4(厘米),画出图即可(答案不唯一);
(2)把这个不规则图形分成两部分,上半部分是个三角形,运用三角形的面积公式即可求出三角形的面积是多少;下半部分是一个梯形,上底是4厘米,下底是3厘米,高是1厘米根据梯形的面积公式:梯形的面积=(上底+下底)×高÷2,再加上上半部分三角形的面积即可。
【详解】(1)
(2)4×1÷2+(4+3)×1÷2
=2+3.5
=5.5(平方厘米)
【点睛】本题主要考查平行四边形,三角形,梯形的面积公式,熟练掌握它们的面积公式并灵活运用即可。
26.113块
【详解】试题分析:首先根据梯形的面积公式:s=(a+b)×2,求出升旗台的面积,再根据正方形的面积公式:s=a2,求出每块方砖的面积,然后升旗台的面积除以每块方砖的面积.据此列式解答.
解:(6+12)×8÷2÷(0.8×0.8),
=18×8÷2÷0.64,
=72÷0.64,
≈113(块);
答:铺砌它一共需要113块方砖.
点评:此题主要考查梯形、正方形面积公式的灵活应用.
27.见详解(画法不唯一);1000棵
【分析】从梯形中分出一个最大的平行四边形,则以梯形较短的底和一条腰作为平行四边形相邻的两条边即可;根据梯形的面积=(上底+下底)×高÷2,平行四边形的面积=底×高,求出剩余的面积,根据1平方米=100平方分米,高级单位转化成低级单位乘进率,换算后再除以9即可求解。
【详解】如图:
(35+26)×20÷2
=61×20÷2
=1220÷2
=610(平方米)
26×20=520(平方米)
610-520=90(平方米)
90平方米=9000平方分米
9000÷9=1000(棵)
答:一共可以种1000棵卷心菜。
【点睛】本题考查梯形和平行四边形的面积公式,要重点掌握。
28.12吨
【详解】试题分析:根据题意,可利用梯形的面积公式(上底+下底)×高÷2计算出这块梯形菜地的面积,然后再用25.2吨白菜除以菜地的面积即可得到答案.
解:菜地的面积为:(150+350)×84÷2
=500×84÷2,
=42000÷2,
=21000(平方米),
21000平方米=2.1公顷,
25.2÷2.1=12(吨),
答:平均每公顷收白菜12吨.
点评:解答此题的关键是确定梯形菜地的面积.
29.2850元
【详解】(6+13)×6÷2×50=2850(元)
30.30千克
【详解】试题分析:此题实际上是求这块梯形广告牌的面积,梯形的上底、下底和高已知,则面积可求;每平方米的用漆量已知,从而能求出总的用漆量.
解:(8+12)×5÷2×0.6,
=20×5÷2×0.6,
=100÷2×0.6,
=50×0.6,
=30(千克);
答:这块广告牌需要30千克油漆.
点评:解答此题的关键是明白:先求出这块梯形广告牌的面积,进而可以求出总的用漆量.
31.90米
【详解】3600×2÷80
=7200÷80
=90(米)
答:菜地三角形的高是90米.
32.4平方厘米
【详解】试题分析:首先我用字母标出各点,从图上可知阴影部分的面积是一个三角形,又知一个底AE的长度是2厘米,只要再求出高来就可以了,又知平行四边形的面积是20平方厘米,其中一底边为2+3=5厘米,再根据求出高来,也就是阴影部分 三角形的高,最后利用三角形的面积公式求出即可.
已知平行四边形的面积是20平方厘米,其中一底边为2+3=5厘米,设高EF为X厘米,
S平行四边形=AD×X,
5X=20,
X=4,
所以,S△ACE=×AE×EF=×2×4=4(平方厘米).
答:阴影部分的面积是4平方厘米.
点评:此题重在根据三角形的面积公式和平行四边形的面积公式的灵活运用.
33.45根
【详解】试题分析:梯形的面积=(上底+下底)×高÷2,将数据代入公式即可求解.
解:(5+10)×6÷2,
=15×6÷2,
=45(根);
答:这批圆木共有45根.
点评:此题主要考查梯形的面积的计算方法在实际生活中的应用.
答案第1页,共2页
答案第1页,共2页
