2023-2024学年内蒙古呼和浩特市回民区高二(下)期末数学试卷(含答案)
文档属性
| 名称 | 2023-2024学年内蒙古呼和浩特市回民区高二(下)期末数学试卷(含答案) | 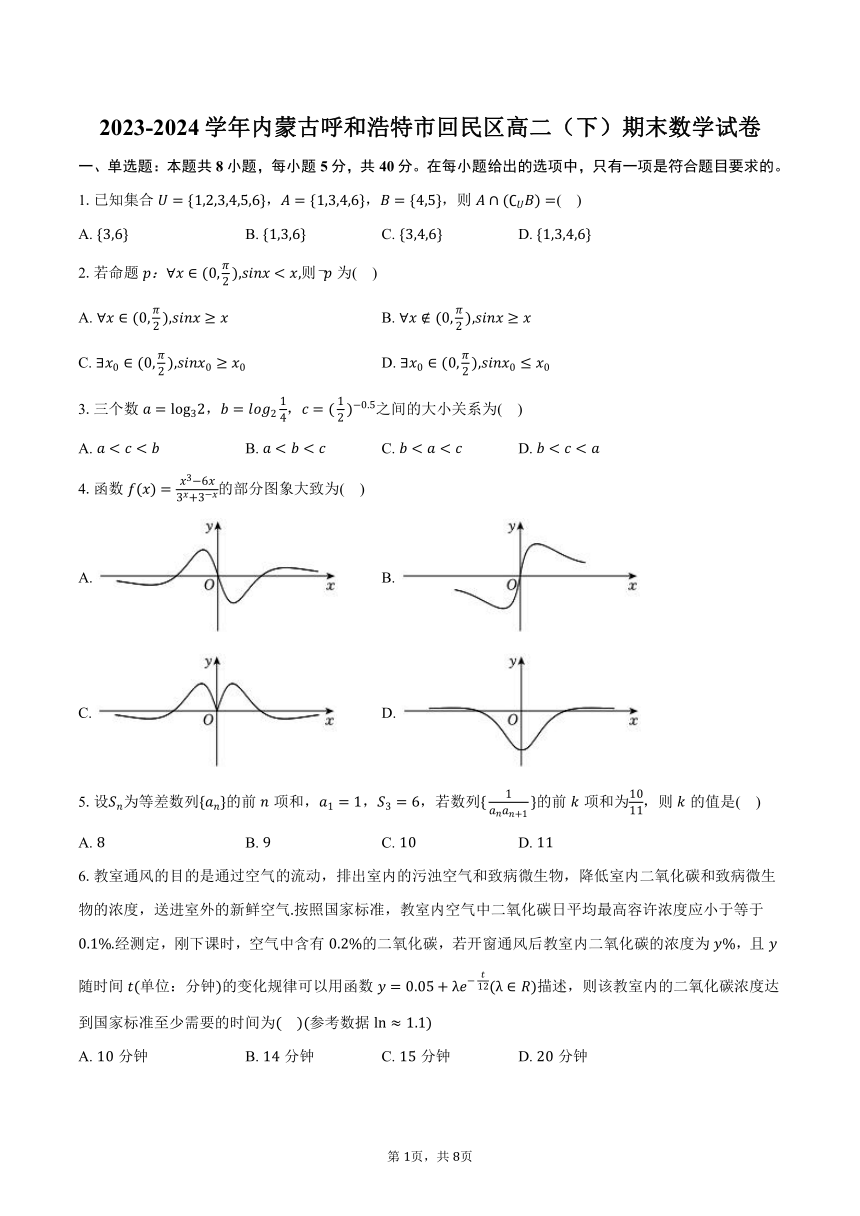 | |
| 格式 | docx | ||
| 文件大小 | 45.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-14 21:22:17 | ||
图片预览




文档简介
2023-2024学年内蒙古呼和浩特市回民区高二(下)期末数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,,,则( )
A. B. C. D.
2.若命题为( )
A. B.
C. D.
3.三个数,,之间的大小关系为( )
A. B. C. D.
4.函数的部分图象大致为( )
A. B.
C. D.
5.设为等差数列的前项和,,,若数列的前项和为,则的值是( )
A. B. C. D.
6.教室通风的目的是通过空气的流动,排出室内的污浊空气和致病微生物,降低室内二氧化碳和致病微生物的浓度,送进室外的新鲜空气按照国家标准,教室内空气中二氧化碳日平均最高容许浓度应小于等于经测定,刚下课时,空气中含有的二氧化碳,若开窗通风后教室内二氧化碳的浓度为,且随时间单位:分钟的变化规律可以用函数描述,则该教室内的二氧化碳浓度达到国家标准至少需要的时间为参考数据
A. 分钟 B. 分钟 C. 分钟 D. 分钟
7.已知是定义在上的偶函数,且在上单调递增,又,则的解集是( )
A. B.
C. D.
8.在平面直角坐标系中,已知,,则的最小值为( )
A. B. C. D.
二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。
9.下列命题中,正确的有( )
A. 最小值是
B. “”是““的充分不必要条件
C. 若,则
D. 函数且的图象恒过定点
10.下列说法正确的是( )
A. 与表示同一个函数
B. 函数的定义域为则函数的定义域为
C. 关于的不等式,使该不等式恒成立的实数的取值范围是
D. 已知关于的不等式的解集为,则不等式的解集为
11.甲和乙两个箱子中各装有个球,其中甲箱中有个红球、个白球,乙箱中有个红球、个白球,下列说法正确的是( )
A. 从甲箱中不放回地取球,在第一次取到红球的条件下,第二次也取到红球的概率为
B. 从甲箱中不放回地每次任取一个球,直至取到白球后停止取球,则抽取两次后停止取球的概率为
C. 从乙箱中有放回地抽取次,则次抽到红球的概率为
D. 从乙箱中不放回地抽取个球,则抽到个红球的概率为
12.对于三次函数,现给出定义:设是函数的导数,是的导数,若方程有实数解,则称点为函数的“拐点”经过探究发现:任何一个三次函数都有“拐点”,任何一个三次函数都有对称中心,且“拐点”就是对称中心已知函数,则( )
A. 函数有三个零点
B. 函数有两个极值点
C. 点是曲线的对称中心
D. 方程有三个不同的实数根
三、填空题:本题共4小题,每小题5分,共20分。
13.已知,则______.
14.已知函数,则的解析式为______.
15.两个等差数列和的前项和分别为、,且,则等于______
16.已知若函数有三个不同的零点,则取值范围是______.
四、解答题:本题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
已知数列满足,且,,成等比数列,
求的通项公式;
设数列的前项和为,求的最小值及此时的值.
18.本小题分
已知函数.
求的极大值点和极小值点
求在区间上的最大值和最小值.
19.本小题分
中欧班列是推进“一带一路”沿线国家道路联通、贸易畅通的重要举措,作为中欧铁路在东北地区的始发站,沈阳某火车站正在不断建设,目前车站准备在某仓库外,利用其一侧原有墙体,建造一面高为,底面积为,且背面靠墙的长方体形状的保管员室,由于保管员室的后背靠墙,无需建造费用,因此,甲工程队给出的报价如下:屋子前面新建墙体的报价为每平方米元,左右两面新建墙体的报价为每平方米元,屋顶和地面以及其他报价共计元,设屋子的左右两面墙的长度均为.
当左右两面墙的长度为多少米时,甲工程队的报价最低?
现有乙工程队也参与此保管员室建造竞标,其给出的整体报价为元;若无论左右两面墙的长度为多少米,乙工程队都能竞标成功,求的取值范围.
20.本小题分
年春节期间,科幻电影流浪地球上映,获得较好的评价,也取得了很好的票房成绩某平台为了解观众对该影片的评价情况评价结果仅有“好评”“差评”,从平台所有参与评价的观众中随机抽取人进行调查,数据如下表所示单位:人:
好评 差评 合计
男性
女性
合计
把列联表补充完整,并判断是否有的把握认为“对该部影片的评价与性别有关”?
若将频率视为概率,从抽取的人中所有给出“好评”的观众中随机抽取人,用随机变量表示被抽到的女性观众的人数,求的分布列和数学期望.
参考公式:,其中.
参考数据:
21.本小题分
已知数列的首项为,且满足.
求证为等差数列,并求出数列的通项公式;
设数列的前项和为,求.
22.本小题分
已知函数.
若,求曲线在点处的切线方程;
若恰有三个零点,求的取值范围.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.解:,
是以公差为的等差数列,
又,,成等比数列,
,即,
解得,又,
所以的通项公式为;
由得,
所以当时,取得最小值,且最小值为.
18.解:函数可得,
令,可得,,当,时,,函数是增函数,时,,函数是减函数,
所以的极大值点为和极小值点为;
由可知,时,函数取得极大值:,时,函数取得极小值:,,
在区间上的最大值,
最小值:.
19.解:设甲工程队的总造价为元,依题意左右两面墙的长度均为,
则屋子前面新建墙体长为,
则,
当且仅当,即时,等号成立,
故当左右两面墙的长度为米时,甲工程队的报价最低为元.
由题意可得,对任意的恒成立,即,
所以,即恒成立,
因为,仅当,即时,等号成立,
所以,
故的取值范围为.
20.解:根据题意得列联表补充完整如下:
好评 差评 合计
男性
女性
合计
,
有的把握认为“对该部影片的评价与性别有关”;
从抽取的人中所有给出“好评”的观众中随机抽取人为女性的概率,
且各次抽取之间互相独立,故,
,
,
的分布列为:
.
21.解:证明:数列的首项为,且满足,
则有,又,
所以数列是以为首项,公差为的等差数列;
则有,
所以.
由得,,
所以,
,
由得,
所以.
22.解:时,,所以,
所以,,
所以曲线在点处的切线方程为,即.
因为,
所以是的一个零点,
因为恰有三个零点,所以方程有两个不为实数根,即方程有两个不为实数根.
令,所以,
令,得,令,得,
所以在区间上单调递增,在区间上单调递减,
当时,的值域为
当时,的值域为,
所以且,所以且,
所以的取值范围是.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,,,则( )
A. B. C. D.
2.若命题为( )
A. B.
C. D.
3.三个数,,之间的大小关系为( )
A. B. C. D.
4.函数的部分图象大致为( )
A. B.
C. D.
5.设为等差数列的前项和,,,若数列的前项和为,则的值是( )
A. B. C. D.
6.教室通风的目的是通过空气的流动,排出室内的污浊空气和致病微生物,降低室内二氧化碳和致病微生物的浓度,送进室外的新鲜空气按照国家标准,教室内空气中二氧化碳日平均最高容许浓度应小于等于经测定,刚下课时,空气中含有的二氧化碳,若开窗通风后教室内二氧化碳的浓度为,且随时间单位:分钟的变化规律可以用函数描述,则该教室内的二氧化碳浓度达到国家标准至少需要的时间为参考数据
A. 分钟 B. 分钟 C. 分钟 D. 分钟
7.已知是定义在上的偶函数,且在上单调递增,又,则的解集是( )
A. B.
C. D.
8.在平面直角坐标系中,已知,,则的最小值为( )
A. B. C. D.
二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。
9.下列命题中,正确的有( )
A. 最小值是
B. “”是““的充分不必要条件
C. 若,则
D. 函数且的图象恒过定点
10.下列说法正确的是( )
A. 与表示同一个函数
B. 函数的定义域为则函数的定义域为
C. 关于的不等式,使该不等式恒成立的实数的取值范围是
D. 已知关于的不等式的解集为,则不等式的解集为
11.甲和乙两个箱子中各装有个球,其中甲箱中有个红球、个白球,乙箱中有个红球、个白球,下列说法正确的是( )
A. 从甲箱中不放回地取球,在第一次取到红球的条件下,第二次也取到红球的概率为
B. 从甲箱中不放回地每次任取一个球,直至取到白球后停止取球,则抽取两次后停止取球的概率为
C. 从乙箱中有放回地抽取次,则次抽到红球的概率为
D. 从乙箱中不放回地抽取个球,则抽到个红球的概率为
12.对于三次函数,现给出定义:设是函数的导数,是的导数,若方程有实数解,则称点为函数的“拐点”经过探究发现:任何一个三次函数都有“拐点”,任何一个三次函数都有对称中心,且“拐点”就是对称中心已知函数,则( )
A. 函数有三个零点
B. 函数有两个极值点
C. 点是曲线的对称中心
D. 方程有三个不同的实数根
三、填空题:本题共4小题,每小题5分,共20分。
13.已知,则______.
14.已知函数,则的解析式为______.
15.两个等差数列和的前项和分别为、,且,则等于______
16.已知若函数有三个不同的零点,则取值范围是______.
四、解答题:本题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
已知数列满足,且,,成等比数列,
求的通项公式;
设数列的前项和为,求的最小值及此时的值.
18.本小题分
已知函数.
求的极大值点和极小值点
求在区间上的最大值和最小值.
19.本小题分
中欧班列是推进“一带一路”沿线国家道路联通、贸易畅通的重要举措,作为中欧铁路在东北地区的始发站,沈阳某火车站正在不断建设,目前车站准备在某仓库外,利用其一侧原有墙体,建造一面高为,底面积为,且背面靠墙的长方体形状的保管员室,由于保管员室的后背靠墙,无需建造费用,因此,甲工程队给出的报价如下:屋子前面新建墙体的报价为每平方米元,左右两面新建墙体的报价为每平方米元,屋顶和地面以及其他报价共计元,设屋子的左右两面墙的长度均为.
当左右两面墙的长度为多少米时,甲工程队的报价最低?
现有乙工程队也参与此保管员室建造竞标,其给出的整体报价为元;若无论左右两面墙的长度为多少米,乙工程队都能竞标成功,求的取值范围.
20.本小题分
年春节期间,科幻电影流浪地球上映,获得较好的评价,也取得了很好的票房成绩某平台为了解观众对该影片的评价情况评价结果仅有“好评”“差评”,从平台所有参与评价的观众中随机抽取人进行调查,数据如下表所示单位:人:
好评 差评 合计
男性
女性
合计
把列联表补充完整,并判断是否有的把握认为“对该部影片的评价与性别有关”?
若将频率视为概率,从抽取的人中所有给出“好评”的观众中随机抽取人,用随机变量表示被抽到的女性观众的人数,求的分布列和数学期望.
参考公式:,其中.
参考数据:
21.本小题分
已知数列的首项为,且满足.
求证为等差数列,并求出数列的通项公式;
设数列的前项和为,求.
22.本小题分
已知函数.
若,求曲线在点处的切线方程;
若恰有三个零点,求的取值范围.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.解:,
是以公差为的等差数列,
又,,成等比数列,
,即,
解得,又,
所以的通项公式为;
由得,
所以当时,取得最小值,且最小值为.
18.解:函数可得,
令,可得,,当,时,,函数是增函数,时,,函数是减函数,
所以的极大值点为和极小值点为;
由可知,时,函数取得极大值:,时,函数取得极小值:,,
在区间上的最大值,
最小值:.
19.解:设甲工程队的总造价为元,依题意左右两面墙的长度均为,
则屋子前面新建墙体长为,
则,
当且仅当,即时,等号成立,
故当左右两面墙的长度为米时,甲工程队的报价最低为元.
由题意可得,对任意的恒成立,即,
所以,即恒成立,
因为,仅当,即时,等号成立,
所以,
故的取值范围为.
20.解:根据题意得列联表补充完整如下:
好评 差评 合计
男性
女性
合计
,
有的把握认为“对该部影片的评价与性别有关”;
从抽取的人中所有给出“好评”的观众中随机抽取人为女性的概率,
且各次抽取之间互相独立,故,
,
,
的分布列为:
.
21.解:证明:数列的首项为,且满足,
则有,又,
所以数列是以为首项,公差为的等差数列;
则有,
所以.
由得,,
所以,
,
由得,
所以.
22.解:时,,所以,
所以,,
所以曲线在点处的切线方程为,即.
因为,
所以是的一个零点,
因为恰有三个零点,所以方程有两个不为实数根,即方程有两个不为实数根.
令,所以,
令,得,令,得,
所以在区间上单调递增,在区间上单调递减,
当时,的值域为
当时,的值域为,
所以且,所以且,
所以的取值范围是.
第1页,共1页
同课章节目录
