圆应用题专项训练(拔高篇)-数学六年级上册人教版(含解析)
文档属性
| 名称 | 圆应用题专项训练(拔高篇)-数学六年级上册人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 648.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-14 22:48:31 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
圆应用题专项训练(拔高篇)-数学六年级上册人教版
易错题精讲
1.东区广场的一个圆形花坛,周长是37.68米,花坛的面积是多少平方米? 【答案】113.04平方米 【分析】已知圆形花坛的周长是37.68米,根据圆的周长公式C=2πr可知,r=C÷π÷2,由此求出圆形花坛的半径;然后根据圆的面积公式S=πr2,求出花坛的面积。 【详解】圆形花坛的半径: 37.68÷3.14÷2 =12÷2 =6(米) 花坛的面积: 3.14×62 =3.14×36 =113.04(平方米) 答:花坛的面积是113.04平方米。 2.近年来“推窗可见绿、出门即入园”的美好生活逐渐成为大家的所愿所盼。琪琪家旁边新建城的圆形“口袋公园”,最外围是用五彩碎石铺成的道路,琪琪步长大约是50厘米,她绕这个圆形“口袋公园”一圈大约走了314步,这个公园的面积大约是多少平方米? 【答案】1962.5平方米 【分析】根据题意,先用琪琪每步的长度乘步数,求出这个圆形公园的周长;根据圆的周长公式C=2πr可知,r=C÷π÷2,由此求出圆形公园的半径;最后根据圆的面积公式S=πr2,求出这个公园的面积。注意单位的换算:1米=100厘米。 【详解】50厘米=0.5米 公园的周长: 0.5×314=157(米) 公园的半径: 157÷3.14÷2 =50÷2 =25(米) 公园的面积: 3.14×252 =3.14×625 =1962.5(平方米) 答:这个公园的面积大约是1962.5平方米。 3.洋洋和爷爷在体育场散步,他们下午7:00从体育场的同一地点出发,相背而行,他们都沿着体育场的边线走,爷爷每分钟走60米,洋洋走的速度是爷爷的,体育场如下图。 (1)体育场的周长有多少米? (2)5分钟后他们相遇了吗? 【答案】(1)714米;(2)没有 【分析】(1)根据题意可知,体育场的周长=一个直径是100米的圆周长+2个200米,根据圆周长公式:C=πd,用3.14×100+200×2即可求出体育场的周长; (2)把爷爷的速度看作单位“1”,根据分数乘法的意义,用60×即可求出洋洋走的速度,然后用路程÷两人的速度和即可求出从出发到相遇的时间,再和5分钟比较即可。 【详解】(1)3.14×100+200×2 =314+400 =714(米) 答:体育场的周长有714米。 (2)60×=65(米) 714÷(60+65) =714÷125 =(分钟) >5 答:5分钟后他们还没有相遇。
跟踪训练
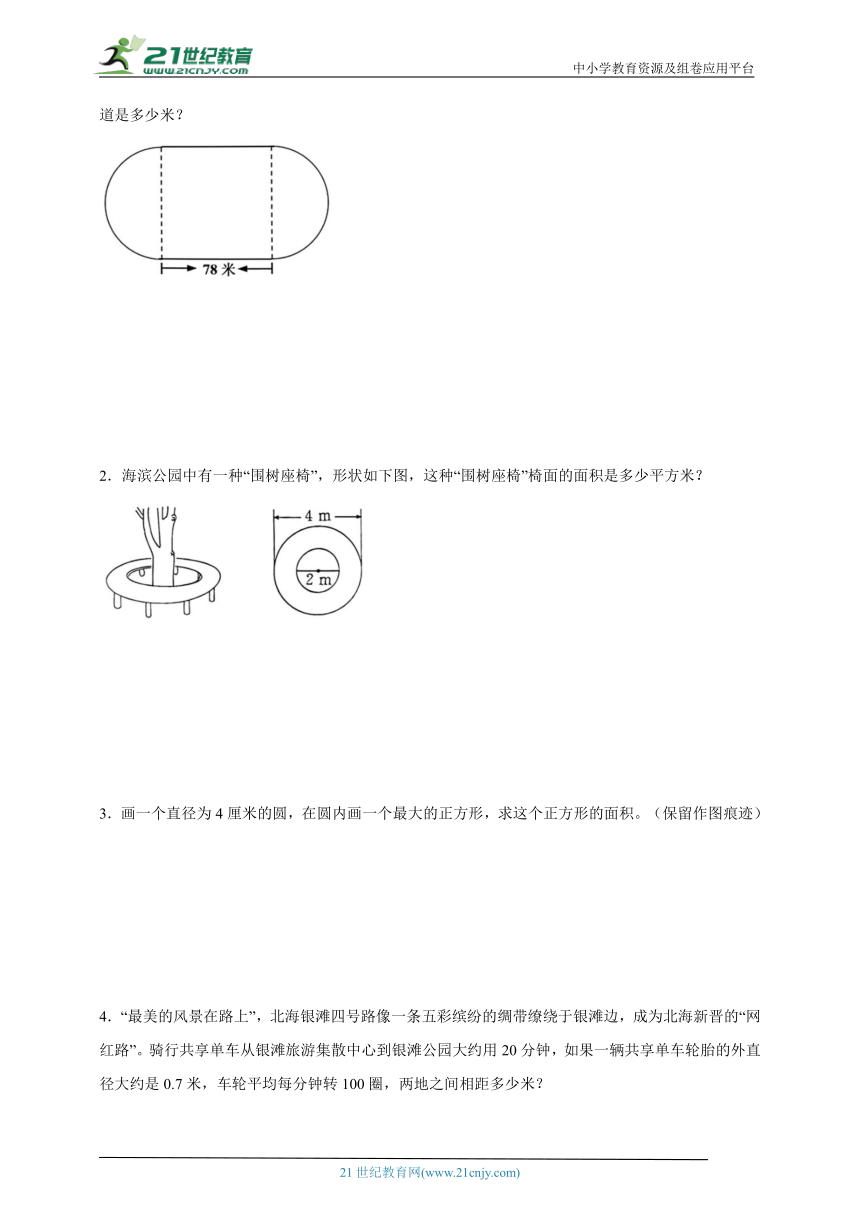
1.下图是某学校操场的形状,跑道最内侧边缘由正方形的一组对边和两个半圆组成。学校操场的跑道是多少米?
2.海滨公园中有一种“围树座椅”,形状如下图,这种“围树座椅”椅面的面积是多少平方米?
3.画一个直径为4厘米的圆,在圆内画一个最大的正方形,求这个正方形的面积。(保留作图痕迹)
4.“最美的风景在路上”,北海银滩四号路像一条五彩缤纷的绸带缭绕于银滩边,成为北海新晋的“网红路”。骑行共享单车从银滩旅游集散中心到银滩公园大约用20分钟,如果一辆共享单车轮胎的外直径大约是0.7米,车轮平均每分钟转100圈,两地之间相距多少米?
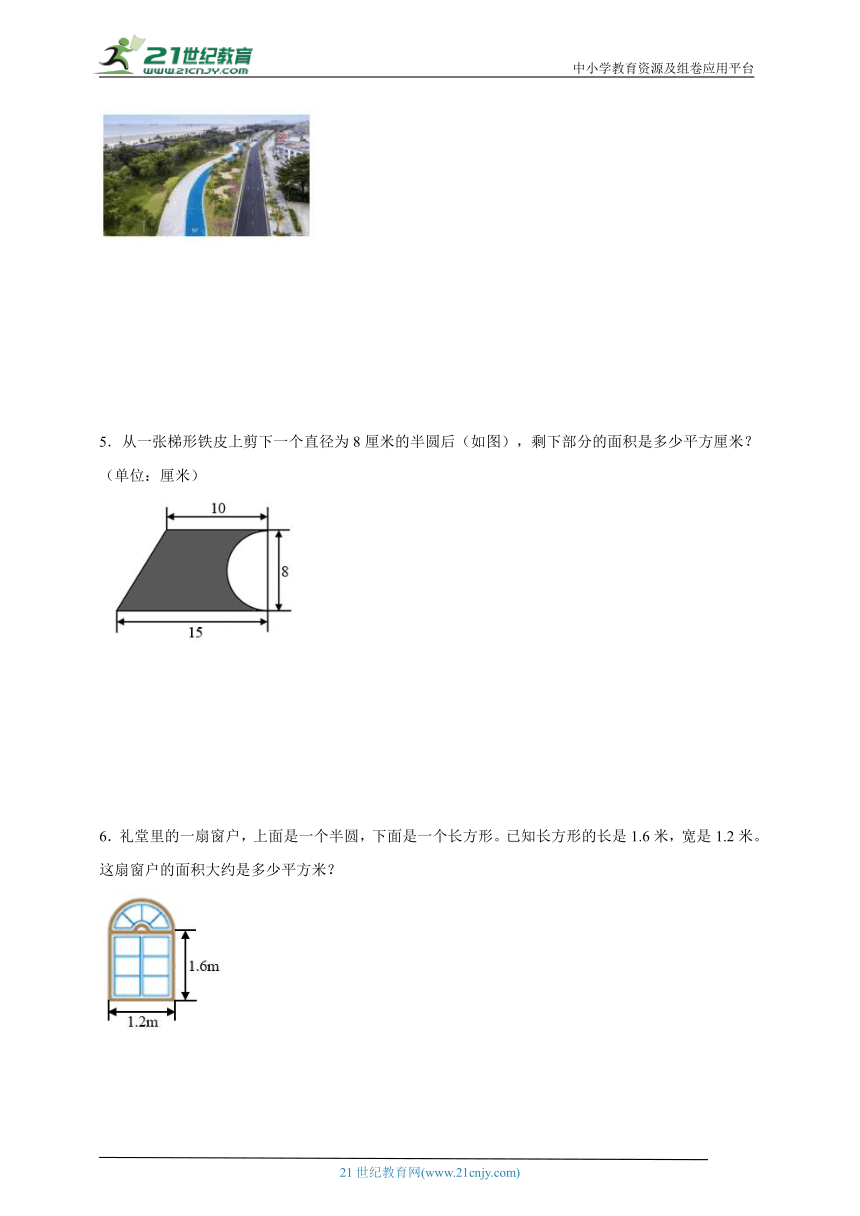
5.从一张梯形铁皮上剪下一个直径为8厘米的半圆后(如图),剩下部分的面积是多少平方厘米?(单位:厘米)
6.礼堂里的一扇窗户,上面是一个半圆,下面是一个长方形。已知长方形的长是1.6米,宽是1.2米。这扇窗户的面积大约是多少平方米?
7.一个半圆形花坛,一周的长是35.98米。
(1)这个花坛的面积有多大?
(2)如果扩建这个花坛,把半径增加1米,花坛的面积增大多少?
8.2022年2月4日第24届冬季奥林匹克运动会在北京开幕。运动会共设7个大项,15个分项,109个小项,其中观赏度很高的双人花样滑冰项目由中国组合隋文静和韩聪夺冠。下图是双人滑做圆周运动的示意图,女运动员的冰鞋滑过一周约是多少米?(结果保留整数)
9.一只钟表的分针长10厘米,从1时到2时,分针的针尖走过了多少厘米?
10.如图所示,这是一块长方形草坪,中间有一个圆形花坛。这块草坪的面积是多少平方米?
11.如下图,圆的周长是18.84厘米,圆的面积正好和长方形的面积相等,这个长方形的长是多少厘米?
12.未来小学有一个小小星空观测台(如下图),空白部分是两个星空观测区,阴影部分是绿化区。现在请你求出绿化区的面积?
13.把一个圆分成若干偶数等份,拼成一个近似的长方形,已知长方形的周长比圆的周长多8厘米,这个圆的面积是多少平方厘米?
14.有一个周长是94.2米的圆形草坪,公园准备为它安装自动旋转喷灌装置进行喷灌。
(1)应将这个喷灌装置安装在草坪的什么位置合适?
(2)现有射程为30米、20米、15米三种装置,你认为应选哪种比较合适?为什么呢?
15.照样子用圆规和直尺画出下图,要求正方形的边长为4厘米,再计算出图中空白部分的面积。(保留画图痕迹)
16.盂县体委有一面墙长8米,在中心点用绳子拴着一条狗,绳长3米。这条狗在地面的活动面积最大是多少?
参考答案:
1.400.92米
【分析】观察图形可知,两个半圆可以组成一个圆;圆的直径等于正方形的边长,为78米,学校操场跑道的长度=圆的周长+两条直跑道的长度;根据圆的周长公式C=,代入数据计算即可。
【详解】3.14×78+78×2
=244.92+156
=400.92(米)
答:学校操场的跑道是400.92米。
【点睛】本题主要考查圆的周长公式的灵活运用,熟记公式是解题关键。
2.9.42平方米
【分析】观察图形可知,这种“围树座椅”椅面的面积就是圆环的面积,根据圆环的面积公式:S=π(R2-r2),据此计算即可。
【详解】3.14×[(4÷2)2-(2÷2)2]
=3.14×[22-12]
=3.14×[4-1]
=3.14×3
=9.42(平方米)
答:这种“围树座椅”椅面的面积是9.42平方米。
【点睛】本题考查圆环的面积,熟记公式是解题的关键。
3.8平方厘米
【分析】在圆内画一个最大的正方形,由图分析可知:正方形面积=直径×半径÷2×2,据此解答。
【详解】画图如下:
正方形面积:
4×2÷2×2
=8÷2×2
=4×2
=8(平方厘米)
答:这个正方形面积是8平方厘米。
【点睛】将正方形面积转化为两个底是直径,高是半径的三角形面积,是解答的关键。
4.4396米
【分析】根据圆的周长=πd,求出车轮转1圈行进距离,车轮转1圈行进距离×每分钟转的圈数×分钟数=两地距离,据此列式解答。
【详解】3.14×0.7×100×20
=2.198×100×20
=219.8×20
=4396(米)
答:两地之间相距4396米。
【点睛】关键是掌握并灵活运用圆的周长公式。
5.74.88平方厘米
【分析】剩下部分的面积=梯形面积-半圆面积,梯形面积=(上底+下底)×高÷2,半圆面积=πr2÷2。
【详解】(10+15)×8÷2-3.14×(8÷2)2÷2
=25×8÷2-3.14×42÷2
=100-3.14×16÷2
=100-25.12
=74.88(平方厘米)
答:剩下部分的面积是74.88平方厘米。
【点睛】关键是掌握并灵活运用梯形和圆的面积公式。
6.2.4852平方米
【分析】观察图形可知,这扇窗户的面积=半圆的面积+长方形的面积,根据圆的面积公式S=πr2,长方形的面积公式S=ab,代入数据计算求解。
【详解】半圆的面积:
3.14×(1.2÷2)2÷2
=3.14×0.36÷2
=0.5652(平方米)
长方形的面积:
1.6×1.2=1.92(平方米)
窗户的面积:
0.5652+1.92=2.4852(平方米)
答:这扇窗户的面积大约是2.4852平方米。
【点睛】本题考查组合图形面积的求法,分析组合图形是由哪些基本图形组成,然后看是求几种图形的面积和还是求面积差,根据图形面积公式解答。
7.(1)76.93平方米
(2)23.55平方米
【分析】(1)根据题意,已知半圆形花坛一周的长是35.98米,也就是半圆周长为35.98米;根据半圆周长=圆周长的一半+直径,即C半圆=πr+2r,可知:圆的半径r=C半圆÷(π+2),由此求出半圆形花坛的半径;然后根据圆的面积公式S=πr2,求出一个圆的面积,再除以2,即是这个的花坛的面积。
(2)如果扩建这个花坛,把半径增加1米,求花坛面积增大多少,就是求半圆环的面积;由上一题可知内圆的半径是7米,则外圆的半径是(7+1)米;根据圆环的面积公式S环=π(R2-r2),求出一个圆环的面积,再除以2,即可得解。
【详解】(1)半圆的半径:
35.98÷(3.14+2)
=35.98÷5.14
=7(米)
半圆的面积:
3.14×72÷2
=3.14×49÷2
=153.86÷2
=76.93(平方米)
答:这个花坛的面积是76.93平方米。
(2)7+1=8(米)
3.14×(82-72)÷2
=3.14×(64-49)÷2
=3.14×15÷2
=47.1÷2
=23.55(平方米)
答:花坛的面积增大23.55平方米。
【点睛】本题考查半圆周长计算方法的灵活运用以及圆环面积公式的应用。
8.10米
【分析】根据题意可知,女运动员的冰鞋滑过一周的长度等于半径是1.6米的圆的周长,根据圆的周长计算公式:,代入数据计算即可解题。
【详解】3.14×2×1.6
=6.28×1.6
=10.048
≈10(米)
答:女运动员的冰鞋滑过一周约是10米。
【点睛】熟记圆的周长计算公式,是解答此题的关键。
9.62.8厘米
【分析】根据题意可知,分钟尖端走过的路程是一个圆,分钟的长度就是这个圆的半径,分针从1时到2时正好旋转一周,根据圆的周长公式进行计算即可得到答案。
【详解】3.14×10×2
=31.4×2
=62.8(厘米)
答:分针的针尖走过了62.8厘米。
【点睛】此题主要考查的是圆的周长公式的应用。
10.249.76平方米
【分析】观察题干可知,草坪的面积=长方形的面积-圆的面积,据此利用长方形的面积=长×宽,圆的面积=πr2计算即可解答。
【详解】15×20=300(平方米)
3.14×42
=3.14×16
=50.24(平方米)
300-50.24=249.76(平方米)
答:这块草坪的面积是249.76平方米。
【点睛】本题考查的是组合图形,先观察图形,将不规则图形转化为规则图形来计算。
11.9.42厘米
【分析】根据圆的周长公式C=2πr可知,r=C÷π÷2,由此求出圆的半径r。观察图形可知,长方形的宽b等于圆的半径r;根据圆的面积公式S=πr2,长方形的面积公式S=ab可知,当圆的面积和长方形的面积相等时,即πr2=ab,且b=r,那么长方形的长a=πr,也就是圆周长的一半,据此解答。
【详解】18.84÷2=9.42(厘米)
答:这个长方形的长是9.42厘米。
【点睛】本题考查圆的面积推导过程的应用,明确当圆的面积和长方形的面积相等,且长方形的宽等于圆的半径时,长方形的长等于圆周长的一半。
12.86平方米
【分析】由图可知,绿化区的面积等于正方形面积减去圆的面积,根据正方形的面积=边长×边长,圆的面积=πr2,代入数据进行解答即可。
【详解】20×(10×2)-3.14×102
=20×20-3.14×100
=400-314
=86(平方米)
答:绿化区的面积是86平方米。
【点睛】熟练掌握圆和正方形的面积公式是解题的关键。
13.50.24平方厘米
【分析】把一个圆剪拼成一个近似的长方形,长方形的长等于圆的周长的一半,宽等于圆的半径;拼成的长方形的周长比原来圆的周长增加了2条宽的长度,即增加了2个半径的长度,用增加的周长除以2,即可求出圆的半径;然后根据圆的面积公式S=πr2,求出这个圆的面积。
【详解】圆的半径:
8÷2=4(厘米)
圆的面积:
3.14×42
=3.14×16
=50.24(平方厘米)
答:这个圆的面积是50.24平方厘米。
【点睛】本题考查圆的面积公式推导过程的应用,明确把圆剪拼成一个近似长方形,圆的面积等于长方形的面积,长方形的周长比圆的周长多了2个半径的长度。
14.(1)安装在草坪的15米处位置合适
(2)射程为15米自动喷灌合适,理由见解析
【分析】(1)要明确射程,即圆的半径,根据圆的周长计算方法,得出”r=C÷π÷2”求出半径,即射程;应放在圆心处;
(2)射程和圆的半径一样最合适,据此解答。
【详解】(1)94.2÷3.14÷2
=30÷2
=15(米)
答:应将这个喷灌装置安装在草坪的15米处合适。
(2)选择射程为15米自动喷灌合适。因为草坪的最大半径是15米。
【点睛】答此题应根据圆的周长和半径的关系进行解答,同时考查了圆心决定圆的位置。
15.画图见详解;9.72平方厘米
【分析】(1)先画一个边长为4厘米的正方形;再分别连接正方形两组对边的中点,并以每条连线的两个四等分点为圆心,以4÷2÷2=1(厘米)为半径画4个半圆。
(2)空白部分的面积=正方形的面积-4个半圆的面积。先根据正方形的面积=边长×边长求出正方形的面积;再根据圆的面积求出圆的面积,用圆的面积除以2再乘4求出4个半圆的面积和;最后用正方形的面积减去4个半圆的面积和。
【详解】作图如下:
=16-3.14×12÷2×4
=16-3.14÷2×4
=16-1.57×4
=16-6.28
=9.72(平方厘米)
【点睛】绘图的关键是要确定某个圆或半圆的圆心和半径,因为圆心和半径分别决定圆的位置和大小。
16.14.13平方米
【分析】观察可知,狗的活动范围在半径是3米的圆面积的一半,根据圆面积公式,用3.14×32÷2即可求出狗的活动面积。
【详解】3.14×32÷2
=3.14×9÷2
=14.13(平方米)
答:这条狗在地面的活动面积最大是14.13平方米。
【点睛】本题考查了圆面积公式的灵活应用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
圆应用题专项训练(拔高篇)-数学六年级上册人教版
易错题精讲
1.东区广场的一个圆形花坛,周长是37.68米,花坛的面积是多少平方米? 【答案】113.04平方米 【分析】已知圆形花坛的周长是37.68米,根据圆的周长公式C=2πr可知,r=C÷π÷2,由此求出圆形花坛的半径;然后根据圆的面积公式S=πr2,求出花坛的面积。 【详解】圆形花坛的半径: 37.68÷3.14÷2 =12÷2 =6(米) 花坛的面积: 3.14×62 =3.14×36 =113.04(平方米) 答:花坛的面积是113.04平方米。 2.近年来“推窗可见绿、出门即入园”的美好生活逐渐成为大家的所愿所盼。琪琪家旁边新建城的圆形“口袋公园”,最外围是用五彩碎石铺成的道路,琪琪步长大约是50厘米,她绕这个圆形“口袋公园”一圈大约走了314步,这个公园的面积大约是多少平方米? 【答案】1962.5平方米 【分析】根据题意,先用琪琪每步的长度乘步数,求出这个圆形公园的周长;根据圆的周长公式C=2πr可知,r=C÷π÷2,由此求出圆形公园的半径;最后根据圆的面积公式S=πr2,求出这个公园的面积。注意单位的换算:1米=100厘米。 【详解】50厘米=0.5米 公园的周长: 0.5×314=157(米) 公园的半径: 157÷3.14÷2 =50÷2 =25(米) 公园的面积: 3.14×252 =3.14×625 =1962.5(平方米) 答:这个公园的面积大约是1962.5平方米。 3.洋洋和爷爷在体育场散步,他们下午7:00从体育场的同一地点出发,相背而行,他们都沿着体育场的边线走,爷爷每分钟走60米,洋洋走的速度是爷爷的,体育场如下图。 (1)体育场的周长有多少米? (2)5分钟后他们相遇了吗? 【答案】(1)714米;(2)没有 【分析】(1)根据题意可知,体育场的周长=一个直径是100米的圆周长+2个200米,根据圆周长公式:C=πd,用3.14×100+200×2即可求出体育场的周长; (2)把爷爷的速度看作单位“1”,根据分数乘法的意义,用60×即可求出洋洋走的速度,然后用路程÷两人的速度和即可求出从出发到相遇的时间,再和5分钟比较即可。 【详解】(1)3.14×100+200×2 =314+400 =714(米) 答:体育场的周长有714米。 (2)60×=65(米) 714÷(60+65) =714÷125 =(分钟) >5 答:5分钟后他们还没有相遇。
跟踪训练
1.下图是某学校操场的形状,跑道最内侧边缘由正方形的一组对边和两个半圆组成。学校操场的跑道是多少米?
2.海滨公园中有一种“围树座椅”,形状如下图,这种“围树座椅”椅面的面积是多少平方米?
3.画一个直径为4厘米的圆,在圆内画一个最大的正方形,求这个正方形的面积。(保留作图痕迹)
4.“最美的风景在路上”,北海银滩四号路像一条五彩缤纷的绸带缭绕于银滩边,成为北海新晋的“网红路”。骑行共享单车从银滩旅游集散中心到银滩公园大约用20分钟,如果一辆共享单车轮胎的外直径大约是0.7米,车轮平均每分钟转100圈,两地之间相距多少米?
5.从一张梯形铁皮上剪下一个直径为8厘米的半圆后(如图),剩下部分的面积是多少平方厘米?(单位:厘米)
6.礼堂里的一扇窗户,上面是一个半圆,下面是一个长方形。已知长方形的长是1.6米,宽是1.2米。这扇窗户的面积大约是多少平方米?
7.一个半圆形花坛,一周的长是35.98米。
(1)这个花坛的面积有多大?
(2)如果扩建这个花坛,把半径增加1米,花坛的面积增大多少?
8.2022年2月4日第24届冬季奥林匹克运动会在北京开幕。运动会共设7个大项,15个分项,109个小项,其中观赏度很高的双人花样滑冰项目由中国组合隋文静和韩聪夺冠。下图是双人滑做圆周运动的示意图,女运动员的冰鞋滑过一周约是多少米?(结果保留整数)
9.一只钟表的分针长10厘米,从1时到2时,分针的针尖走过了多少厘米?
10.如图所示,这是一块长方形草坪,中间有一个圆形花坛。这块草坪的面积是多少平方米?
11.如下图,圆的周长是18.84厘米,圆的面积正好和长方形的面积相等,这个长方形的长是多少厘米?
12.未来小学有一个小小星空观测台(如下图),空白部分是两个星空观测区,阴影部分是绿化区。现在请你求出绿化区的面积?
13.把一个圆分成若干偶数等份,拼成一个近似的长方形,已知长方形的周长比圆的周长多8厘米,这个圆的面积是多少平方厘米?
14.有一个周长是94.2米的圆形草坪,公园准备为它安装自动旋转喷灌装置进行喷灌。
(1)应将这个喷灌装置安装在草坪的什么位置合适?
(2)现有射程为30米、20米、15米三种装置,你认为应选哪种比较合适?为什么呢?
15.照样子用圆规和直尺画出下图,要求正方形的边长为4厘米,再计算出图中空白部分的面积。(保留画图痕迹)
16.盂县体委有一面墙长8米,在中心点用绳子拴着一条狗,绳长3米。这条狗在地面的活动面积最大是多少?
参考答案:
1.400.92米
【分析】观察图形可知,两个半圆可以组成一个圆;圆的直径等于正方形的边长,为78米,学校操场跑道的长度=圆的周长+两条直跑道的长度;根据圆的周长公式C=,代入数据计算即可。
【详解】3.14×78+78×2
=244.92+156
=400.92(米)
答:学校操场的跑道是400.92米。
【点睛】本题主要考查圆的周长公式的灵活运用,熟记公式是解题关键。
2.9.42平方米
【分析】观察图形可知,这种“围树座椅”椅面的面积就是圆环的面积,根据圆环的面积公式:S=π(R2-r2),据此计算即可。
【详解】3.14×[(4÷2)2-(2÷2)2]
=3.14×[22-12]
=3.14×[4-1]
=3.14×3
=9.42(平方米)
答:这种“围树座椅”椅面的面积是9.42平方米。
【点睛】本题考查圆环的面积,熟记公式是解题的关键。
3.8平方厘米
【分析】在圆内画一个最大的正方形,由图分析可知:正方形面积=直径×半径÷2×2,据此解答。
【详解】画图如下:
正方形面积:
4×2÷2×2
=8÷2×2
=4×2
=8(平方厘米)
答:这个正方形面积是8平方厘米。
【点睛】将正方形面积转化为两个底是直径,高是半径的三角形面积,是解答的关键。
4.4396米
【分析】根据圆的周长=πd,求出车轮转1圈行进距离,车轮转1圈行进距离×每分钟转的圈数×分钟数=两地距离,据此列式解答。
【详解】3.14×0.7×100×20
=2.198×100×20
=219.8×20
=4396(米)
答:两地之间相距4396米。
【点睛】关键是掌握并灵活运用圆的周长公式。
5.74.88平方厘米
【分析】剩下部分的面积=梯形面积-半圆面积,梯形面积=(上底+下底)×高÷2,半圆面积=πr2÷2。
【详解】(10+15)×8÷2-3.14×(8÷2)2÷2
=25×8÷2-3.14×42÷2
=100-3.14×16÷2
=100-25.12
=74.88(平方厘米)
答:剩下部分的面积是74.88平方厘米。
【点睛】关键是掌握并灵活运用梯形和圆的面积公式。
6.2.4852平方米
【分析】观察图形可知,这扇窗户的面积=半圆的面积+长方形的面积,根据圆的面积公式S=πr2,长方形的面积公式S=ab,代入数据计算求解。
【详解】半圆的面积:
3.14×(1.2÷2)2÷2
=3.14×0.36÷2
=0.5652(平方米)
长方形的面积:
1.6×1.2=1.92(平方米)
窗户的面积:
0.5652+1.92=2.4852(平方米)
答:这扇窗户的面积大约是2.4852平方米。
【点睛】本题考查组合图形面积的求法,分析组合图形是由哪些基本图形组成,然后看是求几种图形的面积和还是求面积差,根据图形面积公式解答。
7.(1)76.93平方米
(2)23.55平方米
【分析】(1)根据题意,已知半圆形花坛一周的长是35.98米,也就是半圆周长为35.98米;根据半圆周长=圆周长的一半+直径,即C半圆=πr+2r,可知:圆的半径r=C半圆÷(π+2),由此求出半圆形花坛的半径;然后根据圆的面积公式S=πr2,求出一个圆的面积,再除以2,即是这个的花坛的面积。
(2)如果扩建这个花坛,把半径增加1米,求花坛面积增大多少,就是求半圆环的面积;由上一题可知内圆的半径是7米,则外圆的半径是(7+1)米;根据圆环的面积公式S环=π(R2-r2),求出一个圆环的面积,再除以2,即可得解。
【详解】(1)半圆的半径:
35.98÷(3.14+2)
=35.98÷5.14
=7(米)
半圆的面积:
3.14×72÷2
=3.14×49÷2
=153.86÷2
=76.93(平方米)
答:这个花坛的面积是76.93平方米。
(2)7+1=8(米)
3.14×(82-72)÷2
=3.14×(64-49)÷2
=3.14×15÷2
=47.1÷2
=23.55(平方米)
答:花坛的面积增大23.55平方米。
【点睛】本题考查半圆周长计算方法的灵活运用以及圆环面积公式的应用。
8.10米
【分析】根据题意可知,女运动员的冰鞋滑过一周的长度等于半径是1.6米的圆的周长,根据圆的周长计算公式:,代入数据计算即可解题。
【详解】3.14×2×1.6
=6.28×1.6
=10.048
≈10(米)
答:女运动员的冰鞋滑过一周约是10米。
【点睛】熟记圆的周长计算公式,是解答此题的关键。
9.62.8厘米
【分析】根据题意可知,分钟尖端走过的路程是一个圆,分钟的长度就是这个圆的半径,分针从1时到2时正好旋转一周,根据圆的周长公式进行计算即可得到答案。
【详解】3.14×10×2
=31.4×2
=62.8(厘米)
答:分针的针尖走过了62.8厘米。
【点睛】此题主要考查的是圆的周长公式的应用。
10.249.76平方米
【分析】观察题干可知,草坪的面积=长方形的面积-圆的面积,据此利用长方形的面积=长×宽,圆的面积=πr2计算即可解答。
【详解】15×20=300(平方米)
3.14×42
=3.14×16
=50.24(平方米)
300-50.24=249.76(平方米)
答:这块草坪的面积是249.76平方米。
【点睛】本题考查的是组合图形,先观察图形,将不规则图形转化为规则图形来计算。
11.9.42厘米
【分析】根据圆的周长公式C=2πr可知,r=C÷π÷2,由此求出圆的半径r。观察图形可知,长方形的宽b等于圆的半径r;根据圆的面积公式S=πr2,长方形的面积公式S=ab可知,当圆的面积和长方形的面积相等时,即πr2=ab,且b=r,那么长方形的长a=πr,也就是圆周长的一半,据此解答。
【详解】18.84÷2=9.42(厘米)
答:这个长方形的长是9.42厘米。
【点睛】本题考查圆的面积推导过程的应用,明确当圆的面积和长方形的面积相等,且长方形的宽等于圆的半径时,长方形的长等于圆周长的一半。
12.86平方米
【分析】由图可知,绿化区的面积等于正方形面积减去圆的面积,根据正方形的面积=边长×边长,圆的面积=πr2,代入数据进行解答即可。
【详解】20×(10×2)-3.14×102
=20×20-3.14×100
=400-314
=86(平方米)
答:绿化区的面积是86平方米。
【点睛】熟练掌握圆和正方形的面积公式是解题的关键。
13.50.24平方厘米
【分析】把一个圆剪拼成一个近似的长方形,长方形的长等于圆的周长的一半,宽等于圆的半径;拼成的长方形的周长比原来圆的周长增加了2条宽的长度,即增加了2个半径的长度,用增加的周长除以2,即可求出圆的半径;然后根据圆的面积公式S=πr2,求出这个圆的面积。
【详解】圆的半径:
8÷2=4(厘米)
圆的面积:
3.14×42
=3.14×16
=50.24(平方厘米)
答:这个圆的面积是50.24平方厘米。
【点睛】本题考查圆的面积公式推导过程的应用,明确把圆剪拼成一个近似长方形,圆的面积等于长方形的面积,长方形的周长比圆的周长多了2个半径的长度。
14.(1)安装在草坪的15米处位置合适
(2)射程为15米自动喷灌合适,理由见解析
【分析】(1)要明确射程,即圆的半径,根据圆的周长计算方法,得出”r=C÷π÷2”求出半径,即射程;应放在圆心处;
(2)射程和圆的半径一样最合适,据此解答。
【详解】(1)94.2÷3.14÷2
=30÷2
=15(米)
答:应将这个喷灌装置安装在草坪的15米处合适。
(2)选择射程为15米自动喷灌合适。因为草坪的最大半径是15米。
【点睛】答此题应根据圆的周长和半径的关系进行解答,同时考查了圆心决定圆的位置。
15.画图见详解;9.72平方厘米
【分析】(1)先画一个边长为4厘米的正方形;再分别连接正方形两组对边的中点,并以每条连线的两个四等分点为圆心,以4÷2÷2=1(厘米)为半径画4个半圆。
(2)空白部分的面积=正方形的面积-4个半圆的面积。先根据正方形的面积=边长×边长求出正方形的面积;再根据圆的面积求出圆的面积,用圆的面积除以2再乘4求出4个半圆的面积和;最后用正方形的面积减去4个半圆的面积和。
【详解】作图如下:
=16-3.14×12÷2×4
=16-3.14÷2×4
=16-1.57×4
=16-6.28
=9.72(平方厘米)
【点睛】绘图的关键是要确定某个圆或半圆的圆心和半径,因为圆心和半径分别决定圆的位置和大小。
16.14.13平方米
【分析】观察可知,狗的活动范围在半径是3米的圆面积的一半,根据圆面积公式,用3.14×32÷2即可求出狗的活动面积。
【详解】3.14×32÷2
=3.14×9÷2
=14.13(平方米)
答:这条狗在地面的活动面积最大是14.13平方米。
【点睛】本题考查了圆面积公式的灵活应用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
