分数除法应用题专项训练(基础篇)-数学六年级上册苏教版(含解析)
文档属性
| 名称 | 分数除法应用题专项训练(基础篇)-数学六年级上册苏教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 550.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-14 23:01:50 | ||
图片预览




文档简介
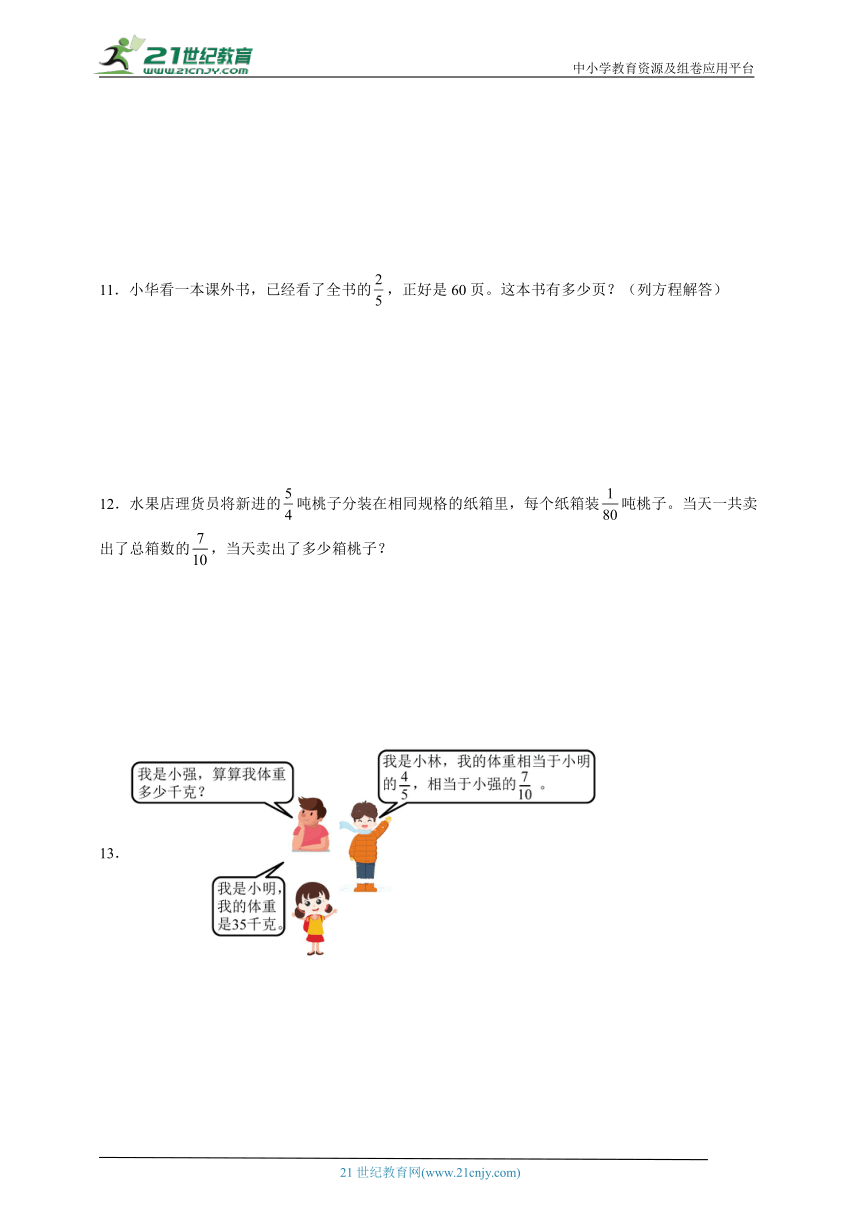
中小学教育资源及组卷应用平台
分数除法应用题专项训练(基础篇)-数学六年级上册苏教版
易错题精讲
1.加工一批零件,已完成任务的,还剩360个没有加工,这批零件共多少个? 【答案】810个 【分析】根据题意,把这批零件的总个数看作单位“1”,已完成任务的,那么还剩下这批零件的(1),然后再根据分数除法的意义,用剩下的零件个数除以剩下的个数占总数的分率即可解答。 【详解】360÷(1) =360 =360× =810(个) 答:这批零件共810个。 2.丁堰小学给教师发放口罩500个,丁堰小学给教师发放的口罩比东方小学的多80个,东方小学给教师发放口罩多少个?(用方程解) 【答案】1260个 【分析】设东方小学给教师发放口罩个,根据等量关系:东方小学给教师发放口罩数量×+80=丁堰小学给教师发放口罩的数量,据此列出方程解方程即可得出答案。 【详解】解:设东方小学给教师发放口罩个。 答:东方小学给教师发放口罩1260个。 3.夏天酸酸甜甜的酸梅汤最受大家喜欢。明明用240毫升的酸梅原汁加水调制了600毫升的酸梅汤。妈妈说:“当酸梅原汁与水的比是3∶7时口感最佳。”明明应该再往酸梅汤里加什么?加多少毫升? 【答案】加水;200毫升 【分析】首先确定应该加酸梅原汁还是加水,分别求出明明配制的酸梅汤中酸梅原汁与水的比并求出比值、妈妈的说法中酸梅汤中酸梅原汁与水的比并求出比值,通过比较即可确定应该加酸梅原汁还是加水。通过计算得知,应该再往酸梅汤加水。按妈妈的说法,当酸梅原汁与水的比是3∶7时口感最佳,则把酸梅原汁看作3份,水看作7份,即水占酸梅原汁的,根据分数乘法的意义,用240毫升乘就是240毫升酸梅原汁应加水的毫升数,用600毫升减240毫升就是已加水的毫升,再用应加水的毫升数减已加水的毫升数。 【详解】 , 应该再往酸梅汤加水 (毫升) 答:明明应该再往酸梅汤里加水,加200毫升。 【点睛】解答此题的关键一是根据明明配制的、妈妈说的,确定应该再往酸梅汤里加水还是再往酸梅原汁;二是按妈妈说的,计算出240毫升原汁需要加水多少毫升,进而计算出再加水多少毫升。
跟踪训练
1.六(1)班积极参加阳光体育活动,有28人参加了跑步,正好占全班人数的,班上还有的同学参加了跳绳,参加跳绳的有多少人?
2.黄大叔种芝麻公顷,是所种玉米的,种的大豆是玉米的,大豆种多少公顷?
3.一块地有公顷,用2台拖拉机耕地,小时可以耕完,平均每台拖拉机每小时耕地多少公顷?(用两种方法解答)
4.“雅馨”花坊上午卖出了百合的,下午又运进480枝百合,这时百合的枝数恰好与原来一样多。“雅馨”花坊原来有百合多少枝?
5.今天妈妈买了一套服装,裤子花了125元,正好是上衣价格的,妈妈买这套衣服一共花了多少钱?
6.水果店上午卖出吨水果,正好占所进水果的,水果店一共进了多少吨水果?(列方程解答)
7.小军和小芳分别从跑道的两端同时出发,相向而行。3分钟后,在离中点15米处相遇。此时,小军和小芳所走的路程比是3∶2。这条跑道长多少米?
8.王师傅加工一批零件,每天加工20个,10天加工了这批零件的。这批零件一共有多少个?
9.小明家装修房子,实际花了24万元,是原计划的,原计划装修需要多少万元?
10.修一条路,已经修了800米,还要修的和已经修的米数的比是5∶4,这条路一共多少米?
11.小华看一本课外书,已经看了全书的,正好是60页。这本书有多少页?(列方程解答)
12.水果店理货员将新进的吨桃子分装在相同规格的纸箱里,每个纸箱装吨桃子。当天一共卖出了总箱数的,当天卖出了多少箱桃子?
13.
14.六(1)班男女生人数比是12∶11,又转来4名女生后,全班共有50人,求原来六(1)班男生有几人?
15.世界上最小的洲是大洋洲面积大约是900万平方千米,是欧洲面积的。欧洲的面积大约是多少万平方千米?
16.爸爸的身高是180厘米小明的身高是爸爸的,小明和妈妈的身高比是7∶8,妈妈的身高是多少厘米?
17.一堆450吨的水泥,按7∶2分给甲、乙两个工地。这两个工地各分得多少吨水泥?
18.王师傅生产一批机器零件,第一周生产了240个,正好占生产任务的,第二周完成任务的。王师傅第二周生产了多少个零件?
参考答案:
1.7人
【分析】将全班人数看作单位“1”,参加跑步的人数÷对应分率=全班人数,全班人数×参加跳绳的对应分率=参加跳绳的人数,据此列式解答。
【详解】28÷×
=42×
=7(人)
答:参加跳绳的有7人。
【点睛】关键是确定单位“1”,理解分数乘除法的意义。
2.公顷
【分析】将种玉米的面积看成单位“1”,种芝麻的面积是玉米面积的,用÷求出种玉米的面积,再乘即可求出大豆的面积;据此解答。
【详解】÷×
=×
=(公顷)
答:大豆种公顷。
【点睛】本题主要考查“已知一个数的几分之几是多少求这个数用除法”及“求一个数的几分之几是多少”。
3.公顷
【分析】方法一:先用÷2求出1台拖拉机小时耕地的面积,再用÷2÷求出1台拖拉机1小时耕地的面积;
方法二:先用÷求出2台拖拉机1小时耕地的面积,再用÷÷2求出1台拖拉机1小时耕地的面积。
【详解】方法一:÷2÷
=÷
=(公顷)
方法二:÷÷2
=÷2
=(公顷)
答:平均每台拖拉机每小时耕地公顷。
【点睛】本题主要考查分数连除的简单应用,理解题意是解题的关键。
4.1280枝
【分析】原来的百合数量为单位“1”,由题意可知,下午运进的480枝百合恰好是原来的,已知一个数的几分之几是多少,求这个数,用除法列式计算即可。
【详解】480÷
=480×
=1280(枝)
答:“雅馨”花坊原来有百合1280枝。
【点睛】本题重点考查分数除法的应用,也可设原来的百合数量为x枝,根据等量关系:原来的百合数量×=480,列方程求解。
5.500元
【分析】将上衣价格看作单位“1”,裤子价格÷对应分率=上衣价格,上衣价格+裤子价格=一套衣服的价格,据此列式解答。
【详解】125÷+125
=375+125
=500(元)
答:妈妈买这套衣服一共花了500元钱。
【点睛】关键是确定单位“1”,理解分数除法的意义。
6.吨
【分析】设水果店一共进了x吨水果,把所进的水果的吨数看作单位“1”,水果店上午卖出吨,正好占所进水果的,即用所进水果的吨数×=上午卖出的水果的吨数,列方程:x=,解方程,即可解答。
【详解】解:设水果店一共进了x吨水果。
x=
x=÷
x=×
x=
答:水果店一共进了吨水果。
【点睛】本题考查方程的实际应用,利用卖出水果的吨数与所进水果吨数之间的关系,设出未知数,找出相关的量,列方程,解方程。
7.150米
【分析】根据题意,小军和小芳所走的路程比是3∶2,即相同时间内,小军走得多,又因为是在离中点15米处相遇,是指小军超过了中点15米,小芳走的离中点还差15米,此时小军走了全程的3÷(3+2)=,把跑道的长度看作单位“1”,那么15米对应的分率就是-,根据:数量÷对应分率=单位“1”可求得跑道的长度,列式为:15÷(-)。
【详解】3÷(3+2)=
15÷(-)
=15÷
=150(米)
答:这条跑道长150米。
【点睛】本题主要考查比的意义,同时要清楚,小军所走的路程超过了中点,是解题的关键。
8.250个
【分析】根据效率×时间=加工总量,先求出10天加工量,10天加工量对应的占总量分率是,已知一个数的几分之几是多少,求这个数,用乘法,即用10天加工量÷=总量,以此解答。
【详解】20×10÷
=200÷
=200×
=250(个)
答:这批零件一共有250个。
【点睛】解答此题的关键是理解分量÷对应分量占总量的分率=总量,确定单位“1”是关键。
9.36万元
【分析】小明家实际花了24万元,是原计划的,根据“已知一个数的几分之几是多少,求这个数,用除法计算”,用24除以即可求出原计划装修需要多少万元。
【详解】24÷=36(万元)
答:原计划装修需要36万元。
【点睛】本题考查分数除法的应用。已知一个数的几分之几是多少,求这个数,用除法计算。
10.1800米
【分析】根据比的意义,还要修的和已经修的米数的比是5∶4,那么还要修的是已经修的。将已经修的看作单位“1”,用已经修的乘求出还要修的。将已经修的加上还要修的,求出这条路一共多少米。
【详解】800+800×
=800+1000
=1800(米)
答:这条路一共1800米。
【点睛】本题考查了比的应用,解题关键是能根据比找出还要修的是已经修的几分之几。
11.150页
【分析】将这本书总页数看作单位“1”,并设为未知数,再根据“这本书总页数×=60页”这一等量关系列方程解方程即可。
【详解】解:设这本书有x页。
x=60
x=60÷
x=150
答:这本书有150页。
【点睛】本题考查了简易方程的应用,解题关键是找出数量关系并正确列方程。
12.70箱
【分析】新进的桃子总质量÷每个纸箱装的质量=总箱数,将总箱数看作单位“1”,总箱数×卖出的对应分率=卖出的箱数,据此列式解答。
【详解】÷×
=100×
=70(箱)
答:当天卖出了70箱桃子。
【点睛】关键是理解分数乘法的意义,掌握分数乘除法的计算方法。
13.40千克
【分析】先把小明的体重看作单位“1”,已知小明体重有35千克,小林的体重是小明体重的,根据分数乘法的意义,用35×即可求出小林的体重,再把小强的体重看作单位“1”,又已知小林的体重是小强体重的,根据分数除法的意义,用小林的体重除以即可求出小强的体重。
【详解】35×÷
=28÷
=40(千克)
答:小强的体重是40千克。
【点睛】本题考查了分数乘除法的混合应用,明确求一个数的几分之几是多少,用乘法计算;已知一个数的几分之几是多少,求这个数用除法计算。
14.24人
【分析】用现在全班人数减去转来的人数,即可求出原来全班的人数,把原来的人数看作单位“1”,已知原来男女生人数比是12∶11,则原来男生人数占原来全班人数的,根据分数乘法的意义,用原来全班人数乘即可求出原来男生人数。
【详解】50-4=46(人)
46×
=46×
=24(人)
答:原来六(1)班男生有24人。
【点睛】本题可转化为分数乘法应用题来解答,也可用按比分配来解答。
15.1000万平方千米
【分析】把欧洲的面积看作单位“1”,单位“1”未知,根据分数除法的意义,已知一个数的几分之几是多少,求这个数,用除法,用大洋洲的面积除以,即可求出欧洲的面积。
【详解】900÷=1000(万平方千米)
答:欧洲的面积大约是1000万平方千米。
【点睛】此题的解题关键是理解分数除法的意义,掌握已知一个数的几分之几是多少,求这个数的计算方法,从而解决问题。
16.160厘米
【分析】先用爸爸的身高×,求出小明的身高,再根据小明和妈妈的身高比是7∶8,则小明的身高是妈妈身高的,再用小明的身高÷,即可求出妈妈的身高。
【详解】小明和妈妈的身高比是7∶8,小明的身高是妈妈身高的。
180×÷
=140÷
=140×
=160(厘米)
答:妈妈的身高是160厘米。
【点睛】解答本题的关键是利用比的应用,求出小明身高是妈妈身高的几分之几。
17.甲:350吨;乙:100吨
【分析】根据按比例分配,即可求出甲、乙两个工地分的水泥的吨数。
【详解】甲工地:450×
=450×
=350(吨)
乙工地:450-350=100(吨)
答:甲工地分得350吨,乙工地分得100吨。
【点睛】熟练掌握按比例分配问题的知识是解答本题的关键。
18.160个
【分析】将这批零件总数看作单位“1”,先用240除以,求出这批零件总数,再乘即可求出第二周生产的个数。
【详解】240÷×
=480×
=160(个)
答:王师傅第二周生产了160个零件。
【点睛】已知一个数的几分之几是多少,求这个数,用除法计算;求一个数的几分之几是多少,用乘法计算。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
分数除法应用题专项训练(基础篇)-数学六年级上册苏教版
易错题精讲
1.加工一批零件,已完成任务的,还剩360个没有加工,这批零件共多少个? 【答案】810个 【分析】根据题意,把这批零件的总个数看作单位“1”,已完成任务的,那么还剩下这批零件的(1),然后再根据分数除法的意义,用剩下的零件个数除以剩下的个数占总数的分率即可解答。 【详解】360÷(1) =360 =360× =810(个) 答:这批零件共810个。 2.丁堰小学给教师发放口罩500个,丁堰小学给教师发放的口罩比东方小学的多80个,东方小学给教师发放口罩多少个?(用方程解) 【答案】1260个 【分析】设东方小学给教师发放口罩个,根据等量关系:东方小学给教师发放口罩数量×+80=丁堰小学给教师发放口罩的数量,据此列出方程解方程即可得出答案。 【详解】解:设东方小学给教师发放口罩个。 答:东方小学给教师发放口罩1260个。 3.夏天酸酸甜甜的酸梅汤最受大家喜欢。明明用240毫升的酸梅原汁加水调制了600毫升的酸梅汤。妈妈说:“当酸梅原汁与水的比是3∶7时口感最佳。”明明应该再往酸梅汤里加什么?加多少毫升? 【答案】加水;200毫升 【分析】首先确定应该加酸梅原汁还是加水,分别求出明明配制的酸梅汤中酸梅原汁与水的比并求出比值、妈妈的说法中酸梅汤中酸梅原汁与水的比并求出比值,通过比较即可确定应该加酸梅原汁还是加水。通过计算得知,应该再往酸梅汤加水。按妈妈的说法,当酸梅原汁与水的比是3∶7时口感最佳,则把酸梅原汁看作3份,水看作7份,即水占酸梅原汁的,根据分数乘法的意义,用240毫升乘就是240毫升酸梅原汁应加水的毫升数,用600毫升减240毫升就是已加水的毫升,再用应加水的毫升数减已加水的毫升数。 【详解】 , 应该再往酸梅汤加水 (毫升) 答:明明应该再往酸梅汤里加水,加200毫升。 【点睛】解答此题的关键一是根据明明配制的、妈妈说的,确定应该再往酸梅汤里加水还是再往酸梅原汁;二是按妈妈说的,计算出240毫升原汁需要加水多少毫升,进而计算出再加水多少毫升。
跟踪训练
1.六(1)班积极参加阳光体育活动,有28人参加了跑步,正好占全班人数的,班上还有的同学参加了跳绳,参加跳绳的有多少人?
2.黄大叔种芝麻公顷,是所种玉米的,种的大豆是玉米的,大豆种多少公顷?
3.一块地有公顷,用2台拖拉机耕地,小时可以耕完,平均每台拖拉机每小时耕地多少公顷?(用两种方法解答)
4.“雅馨”花坊上午卖出了百合的,下午又运进480枝百合,这时百合的枝数恰好与原来一样多。“雅馨”花坊原来有百合多少枝?
5.今天妈妈买了一套服装,裤子花了125元,正好是上衣价格的,妈妈买这套衣服一共花了多少钱?
6.水果店上午卖出吨水果,正好占所进水果的,水果店一共进了多少吨水果?(列方程解答)
7.小军和小芳分别从跑道的两端同时出发,相向而行。3分钟后,在离中点15米处相遇。此时,小军和小芳所走的路程比是3∶2。这条跑道长多少米?
8.王师傅加工一批零件,每天加工20个,10天加工了这批零件的。这批零件一共有多少个?
9.小明家装修房子,实际花了24万元,是原计划的,原计划装修需要多少万元?
10.修一条路,已经修了800米,还要修的和已经修的米数的比是5∶4,这条路一共多少米?
11.小华看一本课外书,已经看了全书的,正好是60页。这本书有多少页?(列方程解答)
12.水果店理货员将新进的吨桃子分装在相同规格的纸箱里,每个纸箱装吨桃子。当天一共卖出了总箱数的,当天卖出了多少箱桃子?
13.
14.六(1)班男女生人数比是12∶11,又转来4名女生后,全班共有50人,求原来六(1)班男生有几人?
15.世界上最小的洲是大洋洲面积大约是900万平方千米,是欧洲面积的。欧洲的面积大约是多少万平方千米?
16.爸爸的身高是180厘米小明的身高是爸爸的,小明和妈妈的身高比是7∶8,妈妈的身高是多少厘米?
17.一堆450吨的水泥,按7∶2分给甲、乙两个工地。这两个工地各分得多少吨水泥?
18.王师傅生产一批机器零件,第一周生产了240个,正好占生产任务的,第二周完成任务的。王师傅第二周生产了多少个零件?
参考答案:
1.7人
【分析】将全班人数看作单位“1”,参加跑步的人数÷对应分率=全班人数,全班人数×参加跳绳的对应分率=参加跳绳的人数,据此列式解答。
【详解】28÷×
=42×
=7(人)
答:参加跳绳的有7人。
【点睛】关键是确定单位“1”,理解分数乘除法的意义。
2.公顷
【分析】将种玉米的面积看成单位“1”,种芝麻的面积是玉米面积的,用÷求出种玉米的面积,再乘即可求出大豆的面积;据此解答。
【详解】÷×
=×
=(公顷)
答:大豆种公顷。
【点睛】本题主要考查“已知一个数的几分之几是多少求这个数用除法”及“求一个数的几分之几是多少”。
3.公顷
【分析】方法一:先用÷2求出1台拖拉机小时耕地的面积,再用÷2÷求出1台拖拉机1小时耕地的面积;
方法二:先用÷求出2台拖拉机1小时耕地的面积,再用÷÷2求出1台拖拉机1小时耕地的面积。
【详解】方法一:÷2÷
=÷
=(公顷)
方法二:÷÷2
=÷2
=(公顷)
答:平均每台拖拉机每小时耕地公顷。
【点睛】本题主要考查分数连除的简单应用,理解题意是解题的关键。
4.1280枝
【分析】原来的百合数量为单位“1”,由题意可知,下午运进的480枝百合恰好是原来的,已知一个数的几分之几是多少,求这个数,用除法列式计算即可。
【详解】480÷
=480×
=1280(枝)
答:“雅馨”花坊原来有百合1280枝。
【点睛】本题重点考查分数除法的应用,也可设原来的百合数量为x枝,根据等量关系:原来的百合数量×=480,列方程求解。
5.500元
【分析】将上衣价格看作单位“1”,裤子价格÷对应分率=上衣价格,上衣价格+裤子价格=一套衣服的价格,据此列式解答。
【详解】125÷+125
=375+125
=500(元)
答:妈妈买这套衣服一共花了500元钱。
【点睛】关键是确定单位“1”,理解分数除法的意义。
6.吨
【分析】设水果店一共进了x吨水果,把所进的水果的吨数看作单位“1”,水果店上午卖出吨,正好占所进水果的,即用所进水果的吨数×=上午卖出的水果的吨数,列方程:x=,解方程,即可解答。
【详解】解:设水果店一共进了x吨水果。
x=
x=÷
x=×
x=
答:水果店一共进了吨水果。
【点睛】本题考查方程的实际应用,利用卖出水果的吨数与所进水果吨数之间的关系,设出未知数,找出相关的量,列方程,解方程。
7.150米
【分析】根据题意,小军和小芳所走的路程比是3∶2,即相同时间内,小军走得多,又因为是在离中点15米处相遇,是指小军超过了中点15米,小芳走的离中点还差15米,此时小军走了全程的3÷(3+2)=,把跑道的长度看作单位“1”,那么15米对应的分率就是-,根据:数量÷对应分率=单位“1”可求得跑道的长度,列式为:15÷(-)。
【详解】3÷(3+2)=
15÷(-)
=15÷
=150(米)
答:这条跑道长150米。
【点睛】本题主要考查比的意义,同时要清楚,小军所走的路程超过了中点,是解题的关键。
8.250个
【分析】根据效率×时间=加工总量,先求出10天加工量,10天加工量对应的占总量分率是,已知一个数的几分之几是多少,求这个数,用乘法,即用10天加工量÷=总量,以此解答。
【详解】20×10÷
=200÷
=200×
=250(个)
答:这批零件一共有250个。
【点睛】解答此题的关键是理解分量÷对应分量占总量的分率=总量,确定单位“1”是关键。
9.36万元
【分析】小明家实际花了24万元,是原计划的,根据“已知一个数的几分之几是多少,求这个数,用除法计算”,用24除以即可求出原计划装修需要多少万元。
【详解】24÷=36(万元)
答:原计划装修需要36万元。
【点睛】本题考查分数除法的应用。已知一个数的几分之几是多少,求这个数,用除法计算。
10.1800米
【分析】根据比的意义,还要修的和已经修的米数的比是5∶4,那么还要修的是已经修的。将已经修的看作单位“1”,用已经修的乘求出还要修的。将已经修的加上还要修的,求出这条路一共多少米。
【详解】800+800×
=800+1000
=1800(米)
答:这条路一共1800米。
【点睛】本题考查了比的应用,解题关键是能根据比找出还要修的是已经修的几分之几。
11.150页
【分析】将这本书总页数看作单位“1”,并设为未知数,再根据“这本书总页数×=60页”这一等量关系列方程解方程即可。
【详解】解:设这本书有x页。
x=60
x=60÷
x=150
答:这本书有150页。
【点睛】本题考查了简易方程的应用,解题关键是找出数量关系并正确列方程。
12.70箱
【分析】新进的桃子总质量÷每个纸箱装的质量=总箱数,将总箱数看作单位“1”,总箱数×卖出的对应分率=卖出的箱数,据此列式解答。
【详解】÷×
=100×
=70(箱)
答:当天卖出了70箱桃子。
【点睛】关键是理解分数乘法的意义,掌握分数乘除法的计算方法。
13.40千克
【分析】先把小明的体重看作单位“1”,已知小明体重有35千克,小林的体重是小明体重的,根据分数乘法的意义,用35×即可求出小林的体重,再把小强的体重看作单位“1”,又已知小林的体重是小强体重的,根据分数除法的意义,用小林的体重除以即可求出小强的体重。
【详解】35×÷
=28÷
=40(千克)
答:小强的体重是40千克。
【点睛】本题考查了分数乘除法的混合应用,明确求一个数的几分之几是多少,用乘法计算;已知一个数的几分之几是多少,求这个数用除法计算。
14.24人
【分析】用现在全班人数减去转来的人数,即可求出原来全班的人数,把原来的人数看作单位“1”,已知原来男女生人数比是12∶11,则原来男生人数占原来全班人数的,根据分数乘法的意义,用原来全班人数乘即可求出原来男生人数。
【详解】50-4=46(人)
46×
=46×
=24(人)
答:原来六(1)班男生有24人。
【点睛】本题可转化为分数乘法应用题来解答,也可用按比分配来解答。
15.1000万平方千米
【分析】把欧洲的面积看作单位“1”,单位“1”未知,根据分数除法的意义,已知一个数的几分之几是多少,求这个数,用除法,用大洋洲的面积除以,即可求出欧洲的面积。
【详解】900÷=1000(万平方千米)
答:欧洲的面积大约是1000万平方千米。
【点睛】此题的解题关键是理解分数除法的意义,掌握已知一个数的几分之几是多少,求这个数的计算方法,从而解决问题。
16.160厘米
【分析】先用爸爸的身高×,求出小明的身高,再根据小明和妈妈的身高比是7∶8,则小明的身高是妈妈身高的,再用小明的身高÷,即可求出妈妈的身高。
【详解】小明和妈妈的身高比是7∶8,小明的身高是妈妈身高的。
180×÷
=140÷
=140×
=160(厘米)
答:妈妈的身高是160厘米。
【点睛】解答本题的关键是利用比的应用,求出小明身高是妈妈身高的几分之几。
17.甲:350吨;乙:100吨
【分析】根据按比例分配,即可求出甲、乙两个工地分的水泥的吨数。
【详解】甲工地:450×
=450×
=350(吨)
乙工地:450-350=100(吨)
答:甲工地分得350吨,乙工地分得100吨。
【点睛】熟练掌握按比例分配问题的知识是解答本题的关键。
18.160个
【分析】将这批零件总数看作单位“1”,先用240除以,求出这批零件总数,再乘即可求出第二周生产的个数。
【详解】240÷×
=480×
=160(个)
答:王师傅第二周生产了160个零件。
【点睛】已知一个数的几分之几是多少,求这个数,用除法计算;求一个数的几分之几是多少,用乘法计算。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
