苏教版数学四年级下册 《多边形的内角和》课件(共20张PPT)
文档属性
| 名称 | 苏教版数学四年级下册 《多边形的内角和》课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-14 22:54:38 | ||
图片预览






文档简介
(共20张PPT)
多边形的内角和
课前准备
......
三角形的内角和是180°。
我知道三角形有3条边、3个角、3条高。
有几条边就是几边形,比如五边形有5条边、5个角。
可以折一折,还可以撕一撕、拼一拼。
我用量角器量出三角形三个角的度数,然后相加。
我想知道这些多边形有几条高?怎么画高?
三角形的内角和是180°,四边形、五边形、六边形等多边形的内角和是多少?我很想知道。
我也很想知道这些多边形的内角和是多少度?
我觉得四边形比较简单,可以先研究四边形。
?
三角形的内角和是180°。
探究四边形的内角和
量一量
拼一拼
我发现这个四边形有两个直角,直角是90°,
然后我用量角器量出另外两个角的度数,分别是140°和40°,全部加起来得到内角和为360°。
我把四边形的4个内角撕下来,拼一拼,
正好是一个周角,也就是360度。
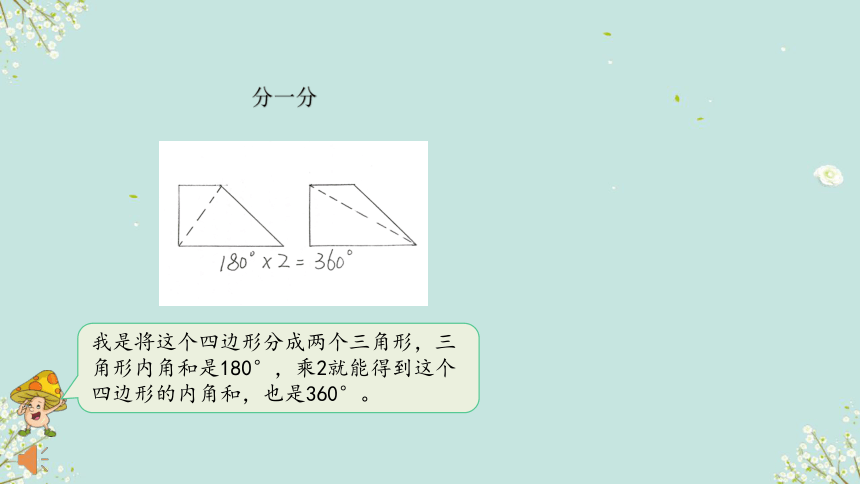
分一分
我是将这个四边形分成两个三角形,三角形内角和是180°,乘2就能得到这个四边形的内角和,也是360°。
方法一:量一量
方法二:拼一拼
方法三:分一分
我觉得第三种方法比较好。
因为量一量有误差,多边形的边数多了,撕一撕很麻烦,有可能拼不了。
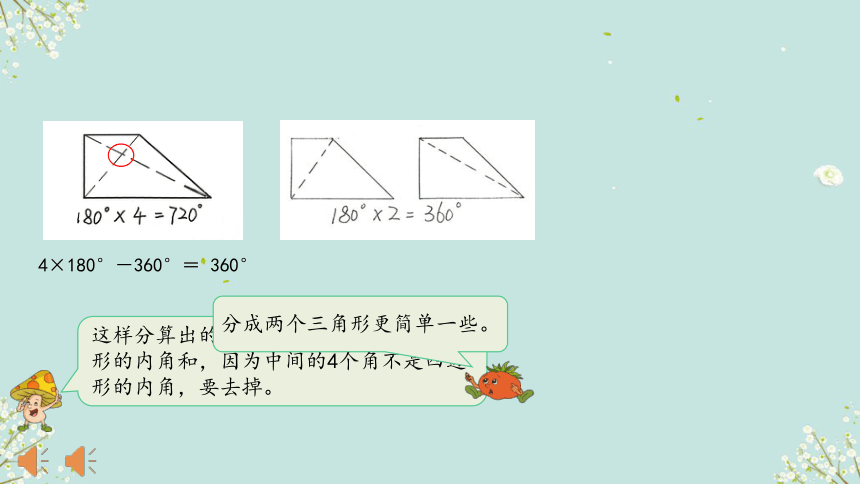
这样分算出的4×180°=720°,不是多边形的内角和,因为中间的4个角不是四边形的内角,要去掉。
分成两个三角形更简单一些。
4×180°-360°= 360°
探究五边形的内角和
180°×3 = 540°
他们的分法其实是一样的,都是把五边形的一个顶点与其他不相邻的两个顶点相连,将五边形分成3个三角形。
这3个三角形内角和加起来,正好是五边形的内角和,可以算出五边形的内角和是 3×180°= 540°。
180 × 4= 720
像这样,将六边形分成4个三角形,
算出六边形内角和是4×180°= 720°。
探究六边形的内角和
1.独立尝试求七边形和八边形的内角和。
2.完成作业单上的表格。
活动要求:
180 ×5=900
七边形
180 ×6=1080
八边形
180 ×5=900
七边形
180 ×6=1080
八边形
180 ×3=540
五边形
六边形
180 ×4=720
他们都是先把多边形分成几个三角形,分别用180 去乘,算出它们的内角和。
3
3
6
4
4
7
5
5
8
6
6
观察比较表中的数据,你有什么发现?
把得到的结果填入下表:
分成的三角形个数 = 边数-2
多边形内角和 =
(多边形的边数-2)×180°
我发现多边形的边数越多,它的内角和就越大。
横着看,四边形分成2个三角形,五边形分成3个三角形......分成的三角形的个数比多边形的边数少2。
为什么多边形分成三角形的个数都比多边形的边数少2?
我发现多边形边数多1,分成三角形的个数增加1,多边形内角和就增加180 。
竖着看,我发现多边形的内角和就等于其分成的三角形个数乘180°。
180 ×3=540
五边形
六边形
180 ×5=900
七边形
180 ×6=1080
八边形
180 ×4=720
因为分成的三角形中,有2个三角形中的两条边是多边形的边,其余三角形,只有一条边是多边形的边,所以分成三角形的个数总比多边形的边数少2。
在分成的三角形中,每个三角形对应多边形的一条边,其中有两个三角形多用了多边形1条边,所以这样分成的三角形个数就比多边形的边数少2。
回顾本节课的学习过程,你有哪些收获?
我学会求一个多边形的内角和,可以根据三角形的内角和推算出来。
我们是从四边形入手,也就是从简单问题入手,接着研究五边形、六边形…这样有序进行研究的。
可以把新的问题转化成能够解决的问题。
拓展延伸
4×180°-360°= 360°
我们可以看成是从四边形内一点和四边形的所有顶点相连,分成4个三角形,所以用4×180 -360 =360 。
课后探究
.
......
.
多边形的内角和
课前准备
......
三角形的内角和是180°。
我知道三角形有3条边、3个角、3条高。
有几条边就是几边形,比如五边形有5条边、5个角。
可以折一折,还可以撕一撕、拼一拼。
我用量角器量出三角形三个角的度数,然后相加。
我想知道这些多边形有几条高?怎么画高?
三角形的内角和是180°,四边形、五边形、六边形等多边形的内角和是多少?我很想知道。
我也很想知道这些多边形的内角和是多少度?
我觉得四边形比较简单,可以先研究四边形。
?
三角形的内角和是180°。
探究四边形的内角和
量一量
拼一拼
我发现这个四边形有两个直角,直角是90°,
然后我用量角器量出另外两个角的度数,分别是140°和40°,全部加起来得到内角和为360°。
我把四边形的4个内角撕下来,拼一拼,
正好是一个周角,也就是360度。
分一分
我是将这个四边形分成两个三角形,三角形内角和是180°,乘2就能得到这个四边形的内角和,也是360°。
方法一:量一量
方法二:拼一拼
方法三:分一分
我觉得第三种方法比较好。
因为量一量有误差,多边形的边数多了,撕一撕很麻烦,有可能拼不了。
这样分算出的4×180°=720°,不是多边形的内角和,因为中间的4个角不是四边形的内角,要去掉。
分成两个三角形更简单一些。
4×180°-360°= 360°
探究五边形的内角和
180°×3 = 540°
他们的分法其实是一样的,都是把五边形的一个顶点与其他不相邻的两个顶点相连,将五边形分成3个三角形。
这3个三角形内角和加起来,正好是五边形的内角和,可以算出五边形的内角和是 3×180°= 540°。
180 × 4= 720
像这样,将六边形分成4个三角形,
算出六边形内角和是4×180°= 720°。
探究六边形的内角和
1.独立尝试求七边形和八边形的内角和。
2.完成作业单上的表格。
活动要求:
180 ×5=900
七边形
180 ×6=1080
八边形
180 ×5=900
七边形
180 ×6=1080
八边形
180 ×3=540
五边形
六边形
180 ×4=720
他们都是先把多边形分成几个三角形,分别用180 去乘,算出它们的内角和。
3
3
6
4
4
7
5
5
8
6
6
观察比较表中的数据,你有什么发现?
把得到的结果填入下表:
分成的三角形个数 = 边数-2
多边形内角和 =
(多边形的边数-2)×180°
我发现多边形的边数越多,它的内角和就越大。
横着看,四边形分成2个三角形,五边形分成3个三角形......分成的三角形的个数比多边形的边数少2。
为什么多边形分成三角形的个数都比多边形的边数少2?
我发现多边形边数多1,分成三角形的个数增加1,多边形内角和就增加180 。
竖着看,我发现多边形的内角和就等于其分成的三角形个数乘180°。
180 ×3=540
五边形
六边形
180 ×5=900
七边形
180 ×6=1080
八边形
180 ×4=720
因为分成的三角形中,有2个三角形中的两条边是多边形的边,其余三角形,只有一条边是多边形的边,所以分成三角形的个数总比多边形的边数少2。
在分成的三角形中,每个三角形对应多边形的一条边,其中有两个三角形多用了多边形1条边,所以这样分成的三角形个数就比多边形的边数少2。
回顾本节课的学习过程,你有哪些收获?
我学会求一个多边形的内角和,可以根据三角形的内角和推算出来。
我们是从四边形入手,也就是从简单问题入手,接着研究五边形、六边形…这样有序进行研究的。
可以把新的问题转化成能够解决的问题。
拓展延伸
4×180°-360°= 360°
我们可以看成是从四边形内一点和四边形的所有顶点相连,分成4个三角形,所以用4×180 -360 =360 。
课后探究
.
......
.
